文章来源于微信公众号（茗创科技），欢迎有兴趣的朋友搜索关注。
导读
强大的非侵入性神经成像技术的可用性引发了各种旨在绘制人类大脑的研究。这些研究不仅聚焦于发现大脑激活信号，还聚焦于理解大脑网络中功能性交流的整体结构。基于不同的大脑区域在功能上相互连接并不断共享信息的原理，文献中提出了寻找这些功能网络的各种方法。在这篇文章中，研究者概述了在fMRI数据中估计和描述功能连接的最常用方法。研究者用人类连接组项目的静息态fMRI数据说明了这些方法，阐述了这些方法的实施细节和对结果解释的见解。本研究的目标是通过提供必要的工具来测量和描述大脑回路，从而指导神经成像领域的新研究人员。
1 引言
功能磁共振成像（fMRI）技术已成为描述人类大脑连接及其与健康、行为和生活方式关系的有力工具。fMRI测量包括基于血氧水平依赖（BOLD）对比的间接的和非侵入性的大脑活动测量。与正电子发射断层扫描（PET）和脑电图（EEG）等替代性脑成像方式相比，fMRI具有无创性和高空间分辨率的特点，这使得其成为大量脑成像研究的热门选择。例如，人类连接项目，该项目旨在通过描述健康成人大脑的连接模式来理解大脑的潜在功能。
这类研究主要有两个目标：第一，识别大脑中对外部刺激做出反应的位置信号；第二，识别大脑在静息态或任务态时出现的大脑时-空关联模式。这些关联模式是解剖学上不同脑区的功能连接时间序列中共同激活的度量，称为功能连接。有证据表明，这些连接模式中的个体差异可以解释个体在认知和行为功能上的重要差异。因此，了解这些模式可以在预测神经退行性疾病的早期发病以及监测疾病护理和治疗方面发挥重要作用。
功能性MRI数据通常是高维的，由一段时间内收集的3D脑体积图像组成。在典型的fMRI研究中，体素Nv的数量是数十万级的，时间点T的数量也是成百上千的。估算体素空间连接性的Nv×Nv相关矩阵是一项具有挑战性的任务，因此在具体研究中进行估算是需要一些策略和前期的假设。一种简单的方法是首先预先选定称为“种子”的脑区，然后计算种子间的相互关系和大脑中其他体素的功能时间序列。这种基于种子的方法计算简单并且容易解释，所以受到研究者的广泛欢迎。种子的大小可以不同，大小可以和单个体素一样小。如果种子是一个区域，则通常将某段时间进程内的信号进行平均，并将其与响应时间段内所有其他体素相关。为了提高可测量性，通常首先将大脑分成几个小的脑区，并使用这些区域的平均时间序列来对脑网络进行估计。当比较精神疾病患者和正常人大脑的运作模式时，基于种子的方法是非常有用的办法。例如，Wang等人(2006)使用基于种子的方法表明，与对照组被试相比，海马体和其他脑区之间的连接会随着阿尔茨海默病的早期症状而改变。尽管基于种子的方法很受欢迎，但是研究者对这种方法仍有各种各样的批评。首先，因为预先确定了特定的种子，所以其他不同脑区出现的潜在模式会被忽略。其次，该方法是对某段时间序列内的ROI进行平均而忽略了体素之间的可变性。第三，该方法只计算了节点对之间的相关性，而忽略了整个网络中其他节点的潜在影响。
与预先指定特定脑区相比，降维法则通过使用少量潜在成分来表示数据，从而描述空间和/或时间连接模式。主成分分析（PCA）和独立成分分析（ICA）是两种最常用的方法。这两种方法都将高维成像数据投射到低维子空间。在PCA中，这种投射由正交成分组成，这些正交成分使投射到低维子空间的数据的方差最大化。在ICA中，投射由尽可能在空间上独立的成分组成。然后，这些成分被组合成具有体素值的地形图，每个体素值表示特定体素的相对数量，受该成分的激活调节。与基于种子的方法相比，PCA和ICA都具有自动化提取成分的优势，无需预先指定种子区域，也就是说这些方法是数据驱动的。Smith等人(2009)使用ICA将大脑网络分解为空间子网络，这些子网络在静息态和任务态fMRI数据中具有相似的功能。
还有一些方法将基于种子的方法中分割脑区的策略与降维方法相结合，来描述大脑神经元回路。Ting等人(2020)使用解剖图预先确定兴趣区（ROIs），然后通过主成分分析的方法从每个聚类中提取特征。然后使用多个提取的成分来估计这些兴趣区之间的连接性，这种连接性使用RV系数来表示，是对特征集之间相关性的度量。
除了用于估计功能连接的方法外，研究者通常还使用图论工具来描述功能网络。在图论中，大脑网络被视为由边连接的节点的集合。通常将脑区之间的功能连接定义为连边。对于指定的节点，通过对功能连接矩阵阈值化，会得到一个二元矩阵。然后，这个二元图谱被用来计算描述大脑网络性质的各种图形参数。这些参数代表了大脑网络的一些关键特征，通常包括有助于确定图节点是以随机秩序连接还是以小世界秩序连接的数量。随机网络的连接模式更具有全局性，而小世界网络则表现出较高的局部秩序性。统计学的网络模型将这些图论测量作为预测具有多个个体特征的全脑网络的输入。
本文的目的是概述在静息态功能磁共振成像数据中估计和描述功能连接性最常用的方法。研究者通过分析人类连接组项目中单个被试的数据来说明这些方法。虽然研究者并不打算详尽地介绍该领域快速发展的方法，但希望本文提供的信息能够指导神经成像领域的新研究人员探索这些数据。
接下来，本文的内容包括以下几个方面：
在第2节中，研究者描述了评估功能连通性的不同方法，主要针对单个被试的数据。在第3节中，使用第2节中描述的方法，来测量人类连接组项目中单个被试静息态数据的功能连接。在第4节中，介绍了几种针对多个被试功能连接估计的方法。在第5节中，描述了统计学网络模型。最后，在第6节中对功能连接进行总结。
2 功能连接的方法
在本节中，研究者将回顾估计单个被试脑功能连接的不同方法。并在第4节中讨论群体脑功能连接性。对于所有计算，研究者假设矩阵Y是大小为T×Nv的矩阵，由表示被试在每个体素v=1,….., Nv上的BOLD信号的Nv时间进程组成。这里，为了简单起见，研究者通过将每个体素数据（列）减去其相应时间过程的平均值来对矩阵Y中心化。无论是在静息态还是任务态中功能连接分析的目标是描述大脑各区域如何相互作用。
2.1 基于种子的分析
计算大量体素之间所有两两成对的相关性在计算上代价是非常大的，因为这需要
次分析。基于种子的分析（SBA）依赖于估计感兴趣区域（ROI）之间或种子区域与大脑中所有其他体素之间的成对相关性。?
为了估计ROI之间的相关性，一种常见的方法是根据解剖模板划分大脑区域，通常称为脑图谱。目前比较常用的脑图谱有AAL、Tailarach图谱和MN1-152图谱。为了估计种子区域和其他体素之间的相关性，研究者通常会根据专家意见来选择种子或选择在功能磁共振成像实验中表现出更大激活的体素作为种子。后一种方法在涉及任务的实验中更常见。选择种子后，通过量化相关性来估计连接性。以往的文献中提出了各种量化的方法。研究者在附录A中提供了关于这些量化方法的更多细节。基于种子的方法汇总如下：
①选择种子脑区或体素；
②将脑区或体素的时间序列与大脑中的所有其他体素计算相关。如果种子是一个脑区，则在将该脑区的时间序列与大脑中的所有其他体素计算相关之前，对该脑区的时间序列求平均值。使用附录A中所述的方法之一；
③呈现相关性的3D像或显示相关性阈值（仅显示达到显著性水平的相关）。注：为了降低假阳的概率，确定显著性，因而需要考虑多重比较。Bonferroni和FDR是两种广泛使用的多重比较校正的方法。
或者，在使用脑图谱将大脑划分为不同的ROI后，可以通过对体素进行平均或计算第一主成分来总括该脑区的时间序列。接下来，研究者使用这些总括的时间序列来与其他所有区域进行相关。研究者在第3节中对这两种选择都进行了说明。
2.2 分解方法
虽然基于种子的方法在解释时比较简单，但在种子选择技术上容易存在偏差，所以在使用时需要谨慎。主成分分析和独立成分分析旨在通过提供功能连接的数据驱动方法来解决这个问题。这些分解方法在功能性神经成像应用中发挥着重要作用。它们在预处理步骤中可以用于去除数据伪影和降低数据维度，并且它们可能会不止出现在一个估计不同人群中的功能连接性步骤中。在本节中，研究者将重点介绍它们在估计单个被试功能磁共振成像数据中功能连接方法中的作用，而在第4节中，将探讨它们在多被试分析中的贡献。
作为基于种子分析的替代方法，分解方法的目标是将体素域表示为空间分量的较小子集。每个空间分量都有一个单独的时间过程，代表许多体素的功能磁共振信号的同时变化。在本节中，研究者假设矩阵Y的每一列数据都减去了平均值。
2.2.1 主成分分析（PCA）
PCA是一种常用的方法，可以降低数据维数，同时最大限度地减少数据信息的损失，最大限度地提高数据的可变性。主成分可以通过两种方式来获得：1.通过样本协方差矩阵YTY的特征分解。2.通过使用奇异值分解（SVD）理论寻找数据矩阵Y的特征向量。
数据矩阵的秩是r=min{T，Nv}（通常是T<Nv和r=T），因此可以通过分解找到r个主成分
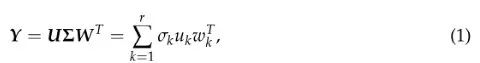
其中T×r矩阵U包含一个正交左奇异向量uk∈RT、r×Nv矩阵W包含正交右奇异向量wk∈RNv，且r×r对角矩阵∑包含有序奇异值。注意，YTY的特征分解定义为WT∑2W。r×Nv矩阵W的正交行被称为特征图像，形成大脑地形图，每个地形图代表由该成分激活所调节的给定体素的相对数量。
另一种方法是将原始的功能磁共振成像数据投射到第一个p主成分所跨越的空间中，其中p的选择基于该成分能够解释数据可变异性指标。投射数据矩阵YW由这个新子空间中的区域时间序列组成。Zhou等人(2009)利用这一想法降低某些ROI中功能磁共振成像数据的维数，然后对两个大脑区域的区组时间序列进行格兰杰因果关系分析，以推断方向连接。虽然可以使用这些投射数据点的时间序列计算相关性，但由于新子空间中的每个空间区域代表原始数据空间中不同体素的线性组合，因此结果没有明确的解释。
2.2.2 独立成分分析（ICA）
ICA旨在使用独立因素的潜在表征来代表大脑数据。与PCA不同，其目标是将Y分解为混合矩阵和空间独立成分（IC）组合的结果。
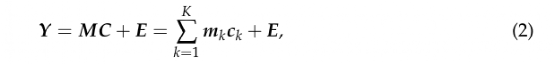
式中，M是带有mk列的T×K混合矩阵，K×Nv矩阵C是带有ck行的独立成分矩阵，其中每个ck包含对应于成分K的大脑网络，总共有K个独立成分。这些成分代表各种功能的网络，如运动、视觉、听觉等。矩阵E是独立的高斯噪声。
假设成分映射（component maps），ck，k=1, .....,?K代表可能的重叠和统计学上的相关信号，但单个成分图谱分布是独立的，即，如果P（ck）表示第K成分图谱中体素值的概率分布，则
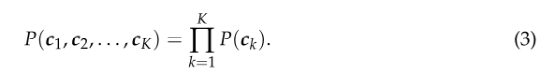
每个独立成分ck是一个Nv大小的向量，可以形成大脑地形图。与PCA一样，这些地形图表示给定体素的相对数量，该体素由该成分的激活调节。
2.3 计算方面
在脑成像应用中，估计主成分需要对Nv×Nv矩阵YTY进行分解，这通常是不可行的。文献中提出了许多算法来有效地估计这种高维环境中的成分。Zou等人(2006)开发了稀疏PCA（SPCA），它基于使用lasso惩罚回归优化估计过程（这种lasso惩罚是指高维环境下的多级函数主成分）通过迭代阈值算法估计主成分的稀疏集。其中一些使用的一些工具包很容易获取，可以在作者的网站上下载。
类似地，估计独立成分并不简单，对成分进行排序也很困难，因为IC通常不是正交的，每个成分解释的方差之和不能与原始数据的方差之和相加。最早的算法之一是Infomax，其目的是最大化适当变换的成分映射的联合熵。最近，更现代的算法侧重于从包含大量特征的数据矩阵中提取稀疏的特征集。例如Le等人(2011)提出的具有重建成本（RICA）的独立成分分析（ICA），在Matlab中有相应的工具箱。
2.4 一种混合方法
Ting等人(2020)给出了估算功能连接的不同方法。作者提出了一个基于多拓扑尺度网络的多尺度模型，从体素水平到由体素聚类组成的脑区，以及由这些脑区的集合组成的更大网络。在实际应用中，这些体素集合是预先指定的，通常被视为解剖学上的ROI。然后，这些ROI可以组合成ROI聚类。他们的方法包括一个维度缩减步骤，直到每个ROI中包含一个因子模型。设r表示第r个ROI，Yr为T×pr数据矩阵，由属于第r个ROI的体素时间序列组成（包含总共的pr体素，其中
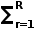
pr=Nv，R为ROI总数）。然后，可以得到这样一个公式
其中，Yr（t）是一个大小为pr的列向量，fr（t）是一个潜在公共因子的mr×1向量，其中有许多因子mr<<pr，Qr是一个mr×pr因子加载矩阵，通过fr的混合定义pr体素之间的依赖关系，而Er（t）=[er1（t），…，erpr（t）]＇是白噪声的pr×1向量，E（Er（t））=0，
=Cov（Er（t））=diag（
，…，
）。然后将这些因子模型连接起来进行定义
其中Y（t）是大小为
pr=Nv的列向量，Q=diag（Q1，…，QR）是一个
pr×
mr块对角混合矩阵，f（t）=[fr（t），…，fR（t）]＇是一个
mr×1聚合潜在因素向量。
这些不同拓扑尺度下的网络协方差矩阵使用低秩矩阵按以下方式进行估计。设
为ROI?r内的协方差矩阵。模型（4）包含以下分解
类似地，从模型（5）中，可以得到
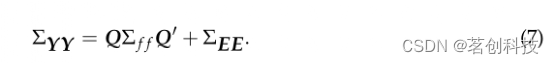
?低维因子协方差矩阵∑ff是一个区组矩阵，用于估计ROI之间的零滞后相关(lag-zero dependency)，如下所示。
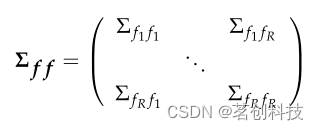
对角线块∑fr fr，r=1,....R是对角协方差矩阵，用于捕获每个ROI内因素的总方差。非对角块∑fk fj，j≠j是因子之间的交叉协方差矩阵，总结了聚类j和k之间的相关性。
作者使用RV系数总结了ROI之间的相关性，RV系数是平方相关系数的多元推广。聚类j和k中因子之间的RV系数定义如下：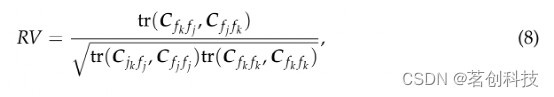
其中
。
在实际估计中，作者应用该模型来估计静息态脑网络。他们使用PCA估计因子fr和矩阵Qr，并根据解剖学上的脑图谱预先指定ROI。Miranda等人(2021)利用人类连接组项目中工作记忆任务的数据，使用这种方法来估计ROI之间的功能连接。
2.5 脑网络
使用图论中的工具来表示大脑是很常见的。在这个框架中，我们可以将功能连接视为一个由图表示的网络，其中空间单元是节点，它们之间的连接是边。网络被视为由连边连接的节点（顶点）的集合。图（网络）表示为G=（V，E）对，其中V和E分别是顶点和边的集合。此外，图形可以加权，在这种情况下，将用三重G=（V，E，W）表示，W（E）表示每条边的权重。
首先要做的是选择网络的节点。与基于种子的估计连接类似，这些节点由体素或脑图谱给出的ROI细分定义。根据节点的规格，必须确定它们的边（连接）。这些边量化了这些不同节点之间的关联强度，即功能连接。前面讨论的功能连接和附录A中描述测量方法用来量化边的强度。
图论分析的大多数标准工具都是由二进制网络开发的，其中每条边要么存在要么不存在。通常称为邻接矩阵的二元矩阵是通过对连通矩阵进行阈值化得到的。虽然使用标准图论机制对加权图进行阈值设置很方便，但在这个过程中，原始信号的信息会有损失。此外，在大多数情况下，阈值的选择不是唯一的，很难说明这样的操作是合理的。一种策略是使用大规模单变量方法，在这种方法中，对网络中的每个可能的连边进行统计测试，然后使用标准技术（如Bonferroni校正或错误发现率（FDR））进行多重比较校正。
在对脑网络进行估计后，计算了一些描述性的度量，作为描述拓扑图性质的手段。在估计脑网络是常用的指标有特征路径长度、集群系数和度分布。有关神经成像中使用的综合拓扑度量的列表，请参见Rubinov等人(2010)的研究。
典型路径长度（Characteristic path length）。路径是不同节点的序列，代表路径较短的成对大脑区域之间的潜在信息流，这意味着整合的潜力更强。路径的长度估计了大脑区域之间功能整合的可能性。功能整合最常用的度量之一是网络中所有节点对之间的平均最短路径长度，它被定义为典型路径长度。断开连接的节点之间的路径被定义为具有无限长，这是计算该度量时的一个问题，尤其是在稀疏网络中，例如在函数连接性中。实际上，研究者只在现有路径之间取平均值，这可能存在一定的问题。关于这个问题的讨论，请参考Rubinov等人(2010)的研究。
节点度分布。作为中心性的一种度量，单个节点的度等于连接到该节点的连边数，即该节点的邻居数。因此，节点度分布就是网络中所有节点的度分布。在功能连接中，高度节点度与网络中的许多其他节点进行功能性交互，称为节点中心。
集群系数。作为分离的一种度量，集群系数是节点的邻居中彼此也是邻居的部分，在图论中是单个节点周围三角形的部分。功能网络中的集群系数表明，一种统计相关性的组织，表示分离的功能性神经加工，即在紧密相连的大脑区域群中进行特定加工的能力。平均而言，网络的平均集群系数反映了单个节点周围的聚集连接的普遍程度。平均集群系数是对每个节点分别进行归一化，并且会受到度值较低节点的不成比例的影响。
许多其他网络指标受基本网络特征的影响很大，例如节点和连边的数量以及本节介绍的分布程度。
3 真实数据示例
研究者分析了来自人类连接组项目（HCP）的静息态数据。选择使用FIX pipeline处理已降噪的数据。使用高通时间滤波器，执行运动回归（即24个运动参数的回归：六个刚体运动参数、它们的后向时间导数和这12个时间序列的平方），并应用基于ICA的回归，以消除与信号成分正交的噪声成分的方差。对于单被试分析，研究者考虑了从示例的右-左阶段（受试者100307）收集的像。每720ms获得一个fMRI像。每个像由大小为91×109×91的图像组成，共有1200个采样点。
3.1 单被试示例
3.1.1 基于ROI的功能连接分析
使用MNI152空间的AAL Atlas版本的脑图谱划分ROI。数据共涉及166个ROI，并使用以下方法估计功能链接：（a）每个ROI中平均时间序列的交叉相关；（b）每个ROI中平均时间序列的偏相关；（c）将ROI数据的时间序列投射到其第一主成分空间的交叉；（d）将ROI数据的时间序列投射到其第一主成分空间的偏相关；（e）对于每个ROI，研究者考虑占ROI变异性20%的主要成分，并计算方程（8）中描述的RV系数。
估计的功能连接结果如图1所示。观察图1可以发现，图片（a）和（c）中的交叉相关比其相应的偏相关（图（b）和（d））捕捉到更大的相关性。图（e）中使用的RV系数方法似乎能够捕捉到大量ROI之间的低相关。在从图中得出任何结论之前，应该首先检验这些值是否显著。对于前四个矩阵，在进行检验时，首先将这些值转换为z分数，然后对它们进行阈值化，以确定重要（显著）的相关。对于图（e）中的RV系数，显著性是基于Ting等人(2020)研究中详述的系数的渐近分布来确定的。
图1.基于AAL分区的ROI的功能连接。图（a）描述了ROI的平均时间序列的交叉相关，图（b）描述了ROI的平均时间序列的偏相关，图（c）描述了与第一偏相关投射的ROI数据的时间序列的交叉相关，图（d）描述了与第一偏相关投射的ROI数据的时间序列的偏相关，图（e）表示RV系数，每个ROI保留了能够解释其20%变异性的主成分。
接下来，研究者使用这些功能连接矩阵可以获得一个二元图，其连边是根据从相关系数的z分数中获得的p值确定的，如附录a中方程（A2）所述。p值根据Bonferroni校正进行了阈值化，显著性为5%。对于图（e）中的RV系数，使用系数的渐近分布将值转换为z分数，并基于Bonferroni校正进行阈值化，以找到显著性为5%的标准正态分布分位数。考虑到这个标准，研究者计算了如图2所示的邻接矩阵。
观察图2可以发现（a）和（c）图都存在大量连边。这表明不同兴趣区之间存在高水平的相互作用。在图（b）和（d）中没有发现这种高水平的相互作用。在图（e）中，可以观察到一些ROI与许多其他ROI之间存在中等程度的相互作用，而在静息态实验期间，一些区域是安静的。
图2.从图1的阈值连接矩阵得到的二元图。
3.1.2 脑网络总结性测量
研究者利用上面获得的二元图，使用第2.5节中所述的图论方法来估计一些总结性测量。各计算中使用的公式详见附录B。表1显示了计算结果。CPL是排除网络中所有无限路径的特征路径长度，DG是脑网络的平均度，其中度表示每个节点中的连边数，CC是脑网络的平均集聚系数，Inf是网络中无限路径的数量。表1中的数值反映了研究者在图2中观察到的情况。度表示兴趣区之间的连接数。正如前面所注意到的，图（a）和（c）中的图说明ROI之间存在很多交互作用，表明度值很高。RV系数的特征路径长度（CPL）表明，平均的脑网络路径长度较短，其值与图2（a）和（c）中的脑网络相当。这表明，尽管连接的区域很少，但连接的区域彼此相邻。
表1 脑网络总结性测量
3.1.3 基于体素的功能连接
基于种子的分析。对于基于种子的分析，研究者选择左侧额下回岛盖部作为种子点。获取该脑区的平均时间序列，并计算与剩余体素的交叉相关。研究者进行了Bonferroni校正，α=0.05，来确定相关性的阈值。图3显示了生成的大脑地形图。研究者将大于125的簇（聚类类别）视为重要体素，将他们覆盖在标准脑上，标准脑由这里使用的示例被试数据的平均时间点组成。
图3.左侧额下回岛盖部的基于种子分析的功能连接。图中显示了带有体素的矢状位切片，这些体素与红色显示的种子ROI有显著的联系。
分解方法。首先获得数据矩阵Y的主成分。需要注意的是，需要大量的主成分来表示数据的可变异性，而传统的主成分具有第2.3节中讨论的问题。对于这一特定数据，需要150个成分来解释20%的数据可变性，需要463个成分来解释50%的数据可变性。研究者在图4中展示了前五个按特征值（即载荷）缩放（降维）的成分。
接下来，为了估计独立成分，研究者使用Beckmann等人(2004)研究中提出的概率独立成分分析，并通过FSL中的MELODIC（多元探索线性优化分解为独立成分）函数实现。图5描述了结果。
为了便于说明，研究者在不设置阈值的情况下呈现成分。在多被试方法中，更常见的是使用单个成分的映射作为输入，然后在群组成分中执行阈值化，以识别群组脑网络。
图4.从第一个（顶部）到第五个（底部）的有序主成分图的矢状位视图。
图5.根据从第一个（顶部）到第五个（底部）不断增加的唯一解释方差对独立成分的地形图进行排序的矢状位视图。
4 多被试的功能连接
在对功能性MRI建模时，一个重要的目标是通过利用跨被试的共享结构来识别多被试数据中的功能连接结构。多被试功能连接模型的范围可以从约束张量分解模型（constrained tensor decomposition models）（例如PARAFAC）到更灵活的方法，其中首先估计特定被试的连接矩阵或PCA和ICA模型，并将其串联结果（concatenated results）用作基于组水平估计的输入。最佳模型将取决于哪一级别的灵活性水平最能捕获组水平的功能连接特征。
在多被试的ICA模型中，一个简单的过程是使用预先指定的ROI（如第2节中描述的基于种子的方法）估计单被试的功能连接，然后将这些结果聚合到单个矩阵中，随后使用主成分进一步对该矩阵进行分解（decomposing）。然后，可以映射主成分以估计基于组水平的功能连接。
Caffo等人(2010)的研究中采用了一种多阶段方法来比较阿尔茨海默病高家族风险被试（临床无症状）与匹配对照组之间的功能连接。该方法遵循四个步骤，包括特定被试的SVD、汇总特定被试特征向量的组水平降维、将单被试水平的数据投射到总体特征向量上以获得特定被试的因子载荷，以及在功能性逻辑回归模型中使用特定被试的因子载荷。
许多研究提出了一种组水平ICA方法，其中，fMRI数据要么跨被试暂时性连接，要么作为多维数组。FMRIB软件库（FSL）是一个包含各种成像数据的图像分析和统计工具的软件库，在其MELODIC函数中提供了组ICA和张量ICA（tensorial ICA）。本节将重点介绍这两种方法。
4.1 组水平ICA
Calhoun等人(2001)的研究中首次提出了对一组被试的fMRI数据进行ICA的方法。假设我们观察n名被试的功能磁共振成像数据。假设Yi是一个大小为T×Nv的矩阵，由Nv个时间序列组成，代表每个体素v=1，...，Nv处的BLOD信号，被试i=1，...，n。他们的模型包括以下多个阶段。
①单个被试水平数据的归约（reduction）。在这一步中，在时域中应用归约（reduction）。对于每个被试i=1，...，n。归约的数据如下所示：
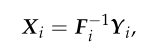
其中
是L×T归约矩阵，Xi是代表归约数据的L×Nv矩阵。实际上，F?1通过PCA分解（decomposition）得到；
②汇总单被试水平数据的归约（reduction）。对NL×Nv矩阵[
，…，
]T进行归约，以获得K×Nv矩阵X=G?1[
，…，
]T，其中K是要获得的组水平成分数量，G?1是一个K×NL归约化矩阵，实际上是由主成分得到的；
③独立成分的估计。ICA分解应用于矩阵X，如第2.2.2节所述。
其中M是K×K混合矩阵，C是K×Nv成分映射矩阵。得到的组水平ICA成分可以通过首先将其转换为Z分数来设定阈值。
可以通过对单个被试划分GM（其中G=（G?1）T）获得个体水平的地形图，并按照如下所示返回前面的步骤。
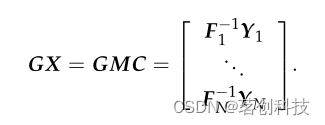
?基于这些步骤，矩阵GMC是单个映射的大小为NL×Nv的矩阵，可以进行分区，因此GiMiCi=
Yi，Ci包含个体水平的地形图。
4.2 张量ICA
张量ICA是基于张量分解的，它可以得到多维数组的低秩表达。PARAFAC是一种常见的分解方法。设X∈RT×Nv×N是一个阵列，分别包含功能磁共振成像数据和时间、体素和被试。三维阵列X可以按以下方式分解为R外积之和
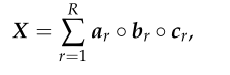
其中
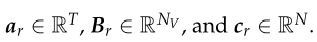
。这种分解意味着数组X中的每个元素都可以写成。
在分解中的向量可以用矩阵表示，例如A= [a1a2?...aR]，同样地，也可以得到矩阵B和C。三维数组可以在一个称为矩阵化的过程中展开为矩阵。展开可以发生在三个维度中的任何一个。在第二维度上，X(2)∈RNv×NT是X的二模矩阵化。类似地，我们可以延伸生成二模和三模矩阵。
关于PARAFAC分解和矩阵化的详细信息，请参考Kolda等人(2009)的研究。根据这些定义，可以将公式写为：
，
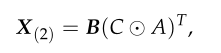
其中☉表示Katri–Rao乘积（product）。Beckmann等人(2005)的研究中提出了方程的ICA分解
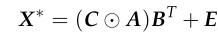
，其中
、混合矩阵
以及成分矩阵BT的估计方法详见Beckmann等人(2004)的研究。
5 统计学网络模型
在本节中，研究者按照Solo等人(2018)研究中的符号来描述统计网络模型，目的是描述大脑网络。在这些模型中，首先使用第2节中的技术估计单个被试的功能连接。估计完单个被试的数据之后，考虑多个感兴趣的变量和拓扑网络特征对整体网络结构的影响。
假设（Yi，Xi）分别代表被试i的脑网络和协变量。给定协变量的网络的概率密度函数用P（Yi?|?Xi，θi）表示，其中θi描述Yi和Xi的关系。这些协变量可以是特定于节点的协变量，如大脑位置，也可以是网络的功能，如路径长度或第2.5节中描述的其他指标。常用的密度函数建模方法包括指数随机图模型（ERGM）和混合模型。
在ERGM中，研究者认为二元图和模型适用于每个被试，如下所示。设Yi是一个由R×R节点组成的网络。然后，如果节点j和k之间存在连接，则Yijk=1，否则Yijk=0。概率质量函数具有正则指数族的形式：
参数θ的估计使用MCMC ML方法完成。在Simpson等人(2012)的研究中确定了每个受试者网络中最重要的解释性指标g（yi）。接下来，为所有被试创建一个基于组的拟合参数值θ的汇总测量。他们使用这些基于组水平的解释性度量和参数，通过ERGM来拟合基于组水平的代表性网络。
目前的ERGM估计方法的一个局限性是其可伸缩性（scalability）。主要问题不是ROI本身的数量，而是脑网络的连边结构，这可能会导致没有办法收敛的问题。此外，大多数模型都是为二元图开发的，不太适合对连边水平上的问题进行检验。作为ERGM的替代方案，混合模型允许连边水平的检查以及多被试的比较。该框架定义了一个由两部分组成的混合效应，对连接存在或不存在的概率以及连接强度（如果存在）进行建模。假设Yi表示附录a中列出的一个相关度量给出的功能连接强度，让Rijk表示j和k之间是否存在连接。那么条件概率是
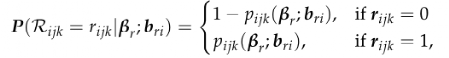
其中，βr是固定效应的向量，该向量与每个参与者和节点对的协变量Xijk相关，而bri是代表特定被试和节点的参数的随机效应。
假设Zijk为与随机效应bri相关的设计矩阵；模型分为两部分。模型的第一部分使用logit链接函数将节点j和k之间的连接概率与协变量联系起来，如下所示。
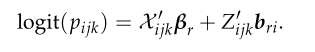
第二部分通过将节点i和j之间的相关系数的Fisher Z变换与协变量线性关联，在存在连接的情况下，对节点j和k之间的连接强度进行建模。让Sijk=Yijk?| Rijk=1，则
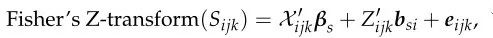
其中，βr是一个总体参数向量，它与每个被试和节点对的同一组协变量Xijk的连接强度相关，bsi是一个被试和节点特定参数向量，它捕捉了这种关系如何随总体平均βs变化，eijk是主体i和节点j和k的随机噪声。Simpson等人(2015)给出了两部分建模方法的详细信息。
这些模型存在一个问题，即使考虑了多重比较，基于连接权重的阈值选择将影响网络拓扑。Solo等人认为，持久同源性提供了一个解决阈值问题的多尺度层次框架。该方法是一种计算拓扑技术，为比较网络提供了一致的数学框架。持久同源性记录了拓扑网络特征在多分辨率和多尺度上的变化，而不是以固定阈值观察网络。通过这样做，它揭示了对噪声具有鲁棒性的特征，即最“持久”的拓扑特征。
6 总结
本文回顾了fMRI数据中最常用的功能连接估计的方法。对于单被试数据，可以通过直接量化感兴趣区域和/或种子区域之间的相关性，或通过找到一组代表同时活动的潜在成分来进行估计。前一种方法的在解释上比较简单，而后一种方法的解释则不那么清楚。在提供的示例中，表示数据可变异性所需的成分图数量非常多，因此，仅对少数成分的调查可能无法反映大脑网络的整体情况。第2节中获得的结果表明，即使以等效的方式定义区域，不同的连接估计程序也会导致对脑网络的不同解释。因此，意识到每种方法的局限性是非常重要的，尤其是在解释单个被试数据的结果时。
尽管单被试分析面临挑战，但单被试分析的方法也可以成功地应用于多被试功能连接分析。尤其是如果这个方法不需要多个阶段，而是执行张量ICA框架中的联合估计。其他新兴的多被试脑网络的方法，如持久同源性（persistent homology），是估计大脑回路的一种很有前途的方法，尤其是可伸缩性（scalability）可以实现的话。
原文：Functional Connectivity Methods and Their Applications in fMRI Data.
https://doi.org/10.3390/e24030390
文章来源于微信公众号（茗创科技），欢迎有兴趣的朋友搜索关注。
