[人工智能]MeanShift、K-Means与GMM迭代

MeanShift聚类

又称均值漂移算法，首先需要一个迭代半径r，相似阈值T

对每个数据，作为一个新类，从其位置半径r内，选择满足相似条件的数据，放到一个表中。

计算表内数据的位置均值，数据均值，将新的位置和均值作为该类的特征，重新计算满足相似条件的数据，不断迭代直到收敛。

相当于数据有两个相似条件，一个位置相似条件r，一个数据相似条件T。

K-Means聚类

该方法被称为k均值，首先需要选定k个聚类中心。

对每个数据，计算出最近的聚类中心C，将其放入C类的数据列表中

拿到每个聚类中心列表中的数据，求取数据均值，将该值作为新的数据中心。不断迭代直到中心不再变化

若将数据分为位置数据和特征值，它和meanshift就很像了。

不过区别在于k-means中，类的数量是手动确定的，而mean shift的类数量是迭代自动确定的，并且最坏情况可能是每个数据都是一个类。

GMM聚类

原理

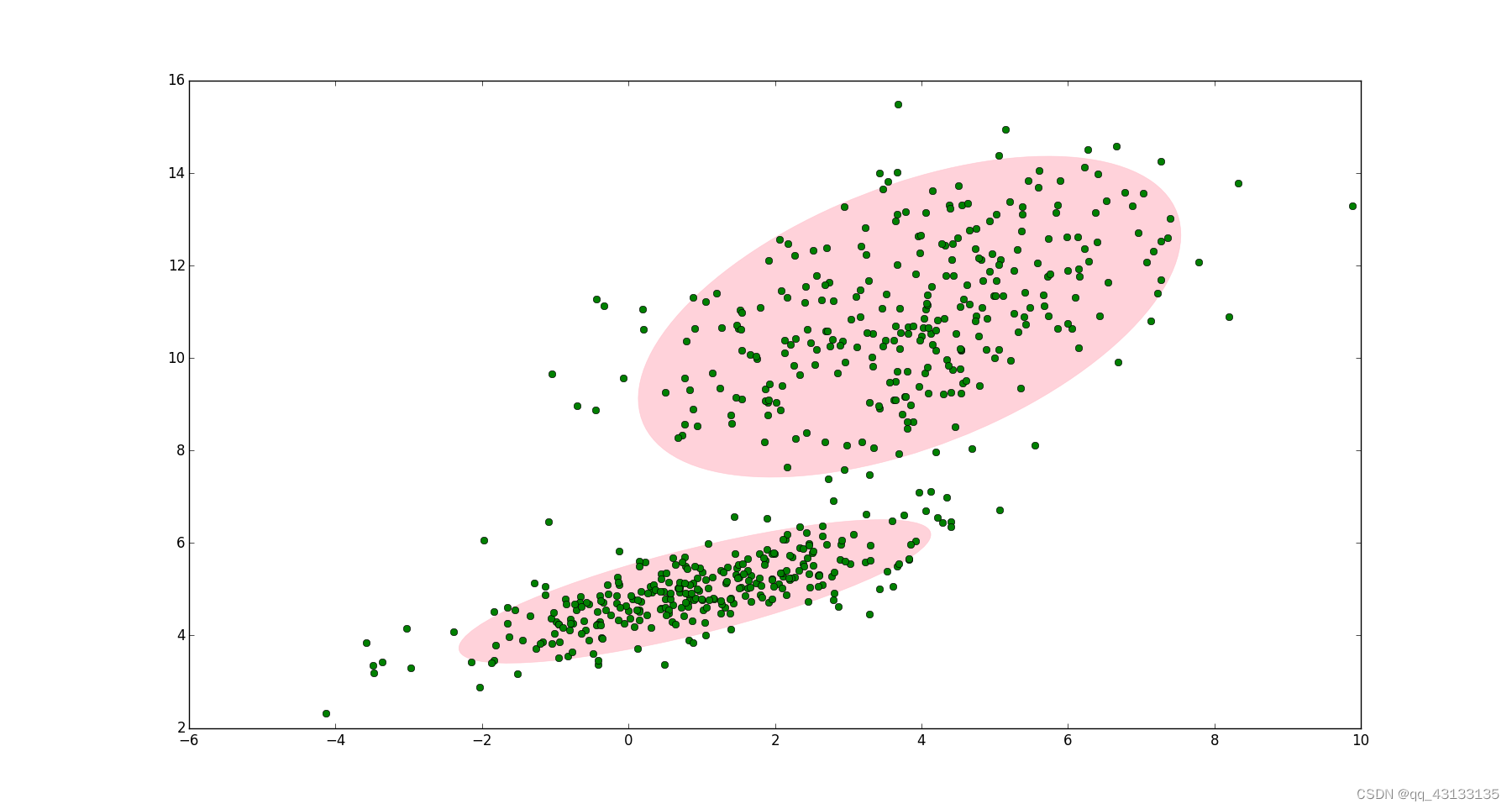
首先，假设数据中有k个高斯分布，数据的实际分布可用其线性组合描述：
$p(\mathbf{x})={\sum }_{k=1}^K{\pi }_k\mathcal{N}(\mathbf{x}|{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k)$

其中$\mathcal{N}(\mathbf{x}|{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k)$称为混合模型中的第k个分量。${\pi }_k$ 是混合系数（或者叫权重、选中该分量的概率），且满足：

1. ${\sum }_{k=1}^K{\pi }_k=1$
2. $0\le {\pi }_k\le 1$

如果要从 GMM 的分布中随机地取一个点的话，实际上可以分为两步：

1. 首先随机地在这 K 个分量之中选一个，每个分量被选中的概率实际上就是它的系数${\pi }_k$

2. 选中之后，再单独地考虑从这个分量的高斯分布中选取一个点就可以了。

EM参数估计

对于GMM中的每个分量，有三个参数：选中概率${\pi }_k$，分布均值${\mu }_k$，分布标准差${\Sigma }_k$。如果我们从分布选取一个点，怎么知道这个点是来自哪个分量呢？或者说如何确定${\pi }_k$？EM算法就可以解决GMM参数估计的问题。

通过EM算法，我们可以迭代计算出GMM中的参数：$({\pi }_k,{\mathbf{x}}_k,{\mathbf{\Sigma }}_k)$。

首先我们可以引入一个新的随机变量 z ∈ { z 1 , z 2 , . . . z k } \boldsymbol{z}∈\{z_1,z_2,...z_k\} z∈{z1?,z2?,...zk?}

$p(z_k)={\pi }_k$，表示第k个分量被选中的概率，由于是每次只能有一个分量被选中，即：

1. ${\sum }_k{z}_k=\Omega$
2. $p(z)={\sum }_{k}p(z_k)={\sum }_k{\pi }_k=1$
3. $p(x|z_k)=\mathcal{N}(\mathbf{x}|{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k)$
4. $p(x)={\sum }_{k}p(x)p(x|z_k)$

根据贝叶斯定理，$p(z)$是先验概率，$p(x\mid z)$是似然概率，$p(z\mid x)$是后验概率。设 x = { x 1 , x 2 , . . . x N } \boldsymbol{x}=\{x_1,x_2,...x_N\} x={x1?,x2?,...xN?}，我们有

1. $p(z\mid x)=p(x\mid z)p(z)$
2. ${\mu }_k=\frac{1}{N_k}{\sum }_{n}p(z\mid x_n)p(x_n)$

EM算法

1. 定义分量数目$k$，对每个分量设置${\pi }_k$、${\mu }_k$和${\mathbf{\Sigma }}_k$ 的初始值，然后计算对数似然函数。

$lnp(x|\pi ,\mu ,\mathbf{\Sigma })={\sum }_{n}ln{\sum }_k{\pi }_{k}N(x_n\mid {\mu }_k,{\mathbf{\Sigma }}_k)$

2. E 阶段: 根据当前的${\pi }_k$、${\mu }_k$和${\mathbf{\Sigma }}_k$ 计算后验概率$\gamma (z_{nk})$

$\gamma (z_{nk})=\frac{{\pi }_{k}N(x_n\mid {\mu }_n,{\mathbf{\Sigma }}_n)}{{\sum }_{j=1}^k{\pi }_{j}N(x_n\mid {\mu }_j,{\mathbf{\Sigma }}_j)}$

3. M阶段：根据E阶段中计算的$\gamma (z_{nk})$再计算新的${\pi }_k$、${\mu }_k$和${\mathbf{\Sigma }}_k$

令 $N_k={\sum }_n\gamma (z_{nk})$ ，则：

1. ${\pi }_k=\frac{N_k}{N}$
2. ${\mu }_k=\frac{1}{N_k}{\sum }_n\gamma (z_{nk})x_n$
3. ${\mathbf{\Sigma }}_k=\frac{1}{N_k}{\sum }_n\gamma (z_{nk})(x_n?{\mu }_k)(x_n?{\mu }_k{)}^T$
   ?

4. 重新计算步骤1中的对数似然函数

5. 检查参数是否收敛或对数似然函数是否收敛，若不收敛，则返回第2步。

其他参考

EM算法
详解EM算法与混合高斯模型
高斯混合模型（GMM）及其EM算法的理解
更多聚类算法参考我另一篇博客：无监督算法

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖