数字图像处理 Ch11 哈里斯-斯蒂芬角检测器
Harris and Stephens 提出了一种角检测算法。
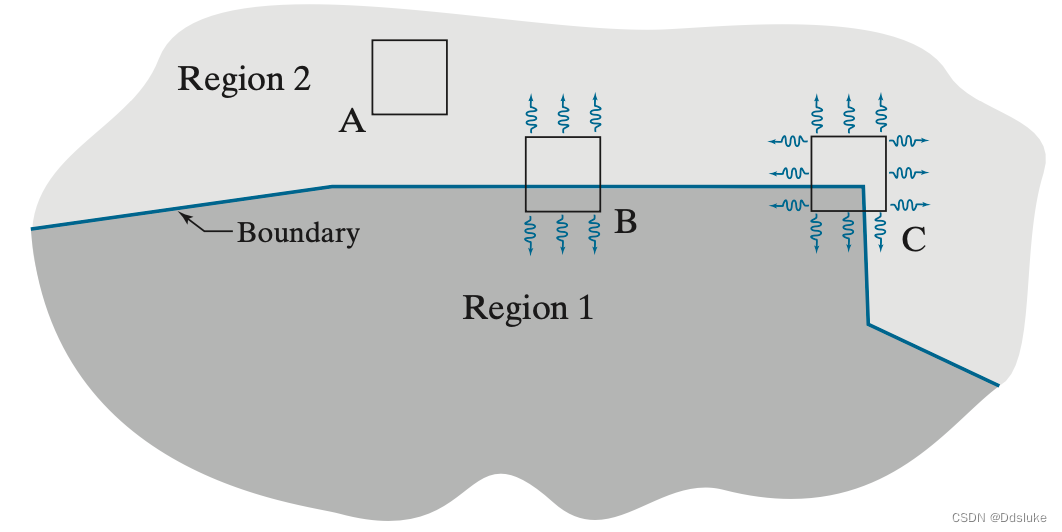
基本思想即为用检测器窗计算灰度变化。如下图，A窗为各个方向上滑动所得到的灰度变化都比较小，B为某个方向上有变化但是其正交方向上不变化，C为所有方向上都发生重大变化。
HS角检测器是试图区分以下ABC三个条件的数学公式。
滑动前&滑动后 对应窗口中的像素点灰度变化 描述如下：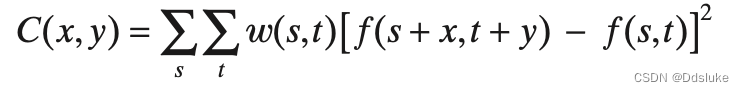
在某些其他文章的描述里面，
C
(
x
,
y
)
C(x,y)
C(x,y)也叫做
E
(
u
,
v
)
E(u,v)
E(u,v)，二者含义是一样的。下文中的描述来源于多篇文章，
u
,
v
u, v
u,v等同于
x
,
y
x, y
x,y，
I
I
I等同于
f
f
f。
我们可以进一步简化上图中的式子。
根据泰勒定理，任何一个函数表达式，均可有泰勒公式进行展开，以逼近原函数：
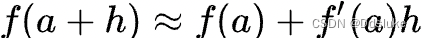
因此我们可以对下面函数
f
(
s
+
x
,
t
+
y
)
f(s+x, t+y)
f(s+x,t+y)进行一阶展开，可以得到：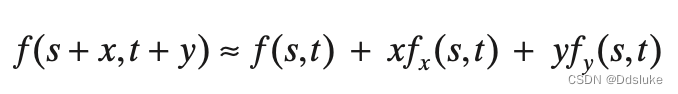
然后代入上式并打开，得到：
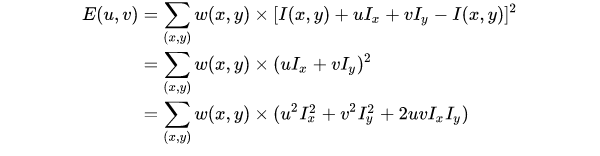
最后，上式可以用矩阵形式写为：
C
(
x
,
y
)
=
[
x
y
]
M
[
x
y
]
C(x,y)=\begin{bmatrix} x & y \end{bmatrix}M \begin{bmatrix} x\\ y \end{bmatrix}
C(x,y)=[x?y?]M[xy?]
其中的
M
M
M如下图（这里的
I
I
I其实就是
f
f
f）：
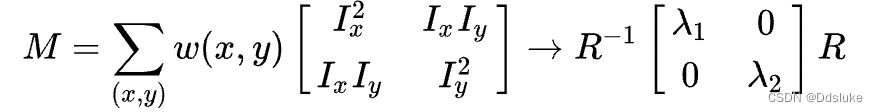
其中
I
x
I_x
Ix?和
I
y
I_y
Iy?是
I
I
I的偏微分，在图像中就是在 x 和 y 方向的梯度图（可以用 cv2.Sobel() 得到）。
w
(
x
,
y
)
w(x,y)
w(x,y)是一个加权函数，一般就两种形式：（1）类似于盒式低通滤波器盒，在小块图像内是1，其他地方是0（左）；（2）高斯函数（右）。
将上式中的实对称矩阵对角化处理，将两个正交方向的变化分量提取出来，就是 λ1 和 λ2（特征值），如上上图。
HS检测器使用了一个角相应测度，这些测度基于一个平方矩阵的迹等于该矩阵的特征值之和，及该矩阵的行列式等于起特征值的积。
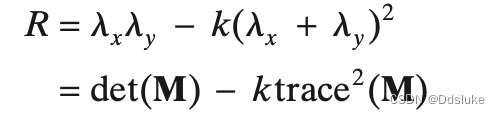
这里k是一个常数，根据经验确定。k的大小有什么意义呢？它可以被看成是一个“敏感因子”，k越小，检测器就越有可能找到角。网上有的说一般在 (0.04, 0.06) 范围内（见下知乎链接），DIP书中默认k值在0.04，也提到MATLAB图像处理工具箱使用的k值域在(0, 0.25)。
两个特征值都较大的时候R有较大的正值，说明存在一个角或者一个孤立的亮点；一个特征值较大的时候但是另一个特征值较小的时候，R有较大的负值，说明存在垂直边界或者水平边界；两个特征值都较小的时候，R绝对值小，说明该小块图像较平坦。
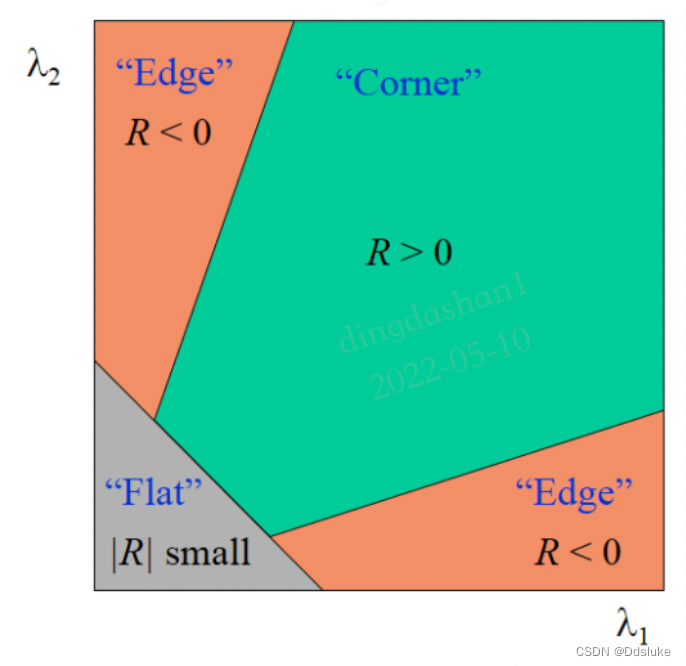
一般配合R会有一个阈值T，R > T就说明检测到了一个角，这个T当然也是需要人为确定的。总而言之，实际运用中，由于图像噪声，可能需要多次修改k、T的值来得到期望的结果。
这几篇博客写得很详细，对我的理解有很大的帮助，笔记中有部分借鉴：
https://blog.csdn.net/lwzkiller/article/details/54633670， https://zhuanlan.zhihu.com/p/83064609
