[人工智能]超分之BasicVSR++

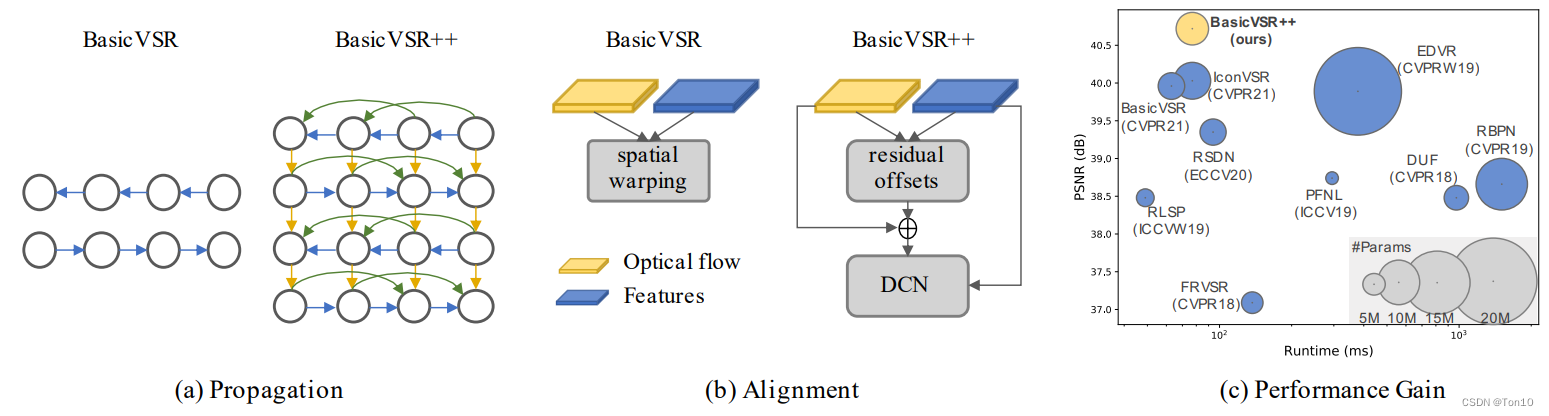
这篇文章是BasicVSR的$升级版本$，同一批作者将BasicVSR中的Propagation和Alignment部分进行了增强产生了新一点VSR方法——BasicVSR++。具体而言，Propagation采用了一个Grid-Propagation来重复校正对齐的准确性；更重要的是提出了一个具有二阶马尔可夫性质的跨格点传播机制以及光流引导的可变形卷积对齐模块。通过这3个改进，Basic++取得了SOTA的表现力以及获得了2021年超分挑战赛NTIRE的冠军！

参考目录：
①源码

Abstract

$BasicVSR\&IconVSR$
BasicVSR利用其双向循环传播结构成功在视频超分的benchmarks上取得了不错的表现力。此外IconVSR在BasicVSR的基础上引入了Coupled-Propagation来使得前向传播的时候可以使用后向传播的信息；Information-refill通过额外的特征提取模块来弥补因为长序列传播累积下来的关于遮挡、边界所造成的对齐误差引起的细节损失。
BasicVSR和IconVSR还是有缺陷的，更何况BasicVSR更多是作为VSR研究的baseline，那么还有哪些改进空间呢？

1. 首先是Propagation部分：①BasicVSR的两个分支是独立进行对齐的，虽然后续会融合，但是如果对齐出现误差，那么融合进行超分会弱化表现力；IconVSR利用Coupled-Propagation将后向分支的对齐结果加入到前向中，的确有助于解决遮挡问题，但是前向的信息是否也可以加入到后向中去呢？答案是可以的，比如对于边界问题，后向在对齐的时候因为没有前面帧关于边界的特征信息，故这部分边界的对齐是找一些不存在不相关的像素去代替的，而这部分不存在的信息就需要前向中的特征信息来帮助补充，IconVSR通过引入information-refill来解决。②两种方法的propagation都是基于一阶马尔可夫性质，每次只接受相邻的隐藏信息$h$，虽然$h$包含了之前较长序列中的特征信息，但是经过长序列的传播，对齐中的误差会使得这一特征信息产生偏差；而且每经过1次对齐，就会对上一次的特征信息有所衰减，而更久的特征信息衰减地越厉害(这就好比正如DRCN中所说，SISR中较深的深层特征提取会损失原始图像的信息，故需要加入skip connection来进行补充)。③虽然IconVSR引入information-refill去缓解长序列对齐造成的误差堆积，但毕竟也是基于稀疏的的关键帧来做，故也只是每隔一定的$intervals$才缓解一下，是否存在着类似于VESPCN、EDVR这种coarse-to-fine的精确化对齐呢？答案是有的，即BasicVSR++的Grid-Propagation。
2. 其次是Alignment部分：虽然两者的对齐都是基于feature-wise，但毕竟也是依靠光流(flow)来做对齐，而flow-based有3个明显的缺陷：①高度依赖于光流估计的精确性，一旦运动估计出错，那么最终在feature map上的warp就会出现artifacts；②two-stage分2步，先做光流估计，然后做隐式的运动补偿(warp)，故速度上会较慢一些；③Flow-based在做对齐的时候，其warp只能根据一个位置通过光流获取像素值，这种做法相对于DCN而言，探索性较差。

Note：

1. 最不可取的就是基于flow-based的image-wise对齐，诸如VESPCN、Robust-LTD这种，因为光流法高度依赖于光流估计的准确性，一旦不准确，就会造成artifacts，且你无法像feature-wise去改善校正它(这一点在TDAN和BasicVSR中有提到)。无论是否基于feature，只要是flow-based这种光流法，那么其相对flow-free也是效果较差的，原因在于其warp的时候只在1个位置点根据光流来获取最终的像素值，探索性较弱容错率较高，这种高度依赖于光流估计精确性的做法会当光流估计不那么准确的时候，就会很容易出现artifacts，那么最终的结果相比DCN这种探索强的方法还是效果差很多，哪怕两者都配备相应的卷积层去调优，相同条件下，光流法一般比不过flow-free，因为flow-free诸如DCN对齐下的探索能力较强，不那么容易出现artifacts；此外在遮挡情境下，flow-free的强探索能力往往会比flow-based产生更好的效果。

$BasicVSR++$
针对上述两个部分，BasicVSR++提出了自己的改进：

1. 针对Propagation部分：先引入Grid-Propagation来让前向和后向分支之间互相建立连接，此外作者又增加了一对前后项分支，让对齐实现coarse-to-fine。更重要的是，引入Second-Order Grid Propagation(二阶格点传播)，说白了，就是当前状态不仅接受相邻格点的隐藏状态，还接受更远1格的隐藏状态，比如说前向分支中，当做$x_{i?1},x_i$的对齐的时候，除了接受$h_{i?1}$之外，还要接受$h_{i?2}$的特征信息。这种做法是有利于遮挡问题和边界问题，通过这种方式来获取更多的特征信息，如位置信息。比如说边界情景中，$x_{i+1}$的特征想要对齐$x_i$的边界特征，但是$x_{i+1}$的特征上没有边界相关的信息，但这时候如果有来自于$x_{i?1}$的特征信息，那么就可以帮助$x_{i+1}$的特征对齐。
2. 针对Alignment部分：既然flow-based方法有那么多缺陷，故直接采用Flow-free方法，诸如TDAN、EDVR中使用的DCN-based对齐方法，因为DCN的对齐方法可以规避上述flow-based中3个缺陷。同时为了解决DCN较难训练的问题，作者引入光流对齐来做辅助对齐(flow-guided deformable alignment)，这样可以减轻DCN去学习对齐的压力。

1. 归功于上述在BasicVSR上的改进，BasicVSR++不仅取得了SOAT的表现力，在和BasicVSR类似的参数量下(BasicVSR++(S)：轻量版本BasicVSR++)，实现了$+0.82dB$的增益，如下图所示：

2. BasicVSR++在NTIRE 2021超分挑战赛获得了3项第一名！

3. 关于BasicVSR和IconVSR的相关内容可参考我的另一篇超分之BasicVSR。

Note：

1. BasicVSR、IconVSR、BasicVSR++属于recurrent方法，都是同一批作者所推出。和sliding-windows方法不同，这三种方式在对齐的时候，被对齐对象并不是参考帧的相邻支持帧的feature map，而是比如前线分支中是当前参考帧之前所有帧的对齐特征$h$，它存储了过去所有对齐的结果，当然由于长距离不断地对齐，输入到当前帧的$h$更加偏向于最近几帧的特征(比如$h_{i?1}$更多是和$x_{i?1}$的特征对齐)，而较远距离的对齐特征就会衰减了一些，后向分支也是一样的情况。

1 Introduction

在BasicVSR中，作者将VSR重新设计分为4个功能块：Propagation、Alignment、Aggregation、Upsampling。

1. Propagation采用双向循环传播机制来利用长序列信息，这种循环机制类似于RNN，它可以将过去或未来的信息存储在隐藏状态中(需要注意的是，这部分隐藏状态在利用的时候是不参与梯度传播的，因此并不涉及到RNN的梯度爆炸或者梯度消失问题)。通过这样的方式来利用整个长序列的特征信息。但是这样的方式也是有问题的：①很久之前或者未来的信息传到当前帧的时候，其特征信息会损失很多，并且不是每个位置的信息都是有用的；②其次对齐误差(首先对齐会设计到网络的预测和插值，所以其值都是估计值，一定会存在着和目标之间的bias，此外还会因为遮挡和边界出现因为不相关的区域而导致无法输出相应对齐像素而导致的误差)会通过这种长序列循环传播机制不断累积，IconVSR通过information-refill来缓解；③两个分支之间没有联系，虽然之后会一起融合，但是那时候一旦出现了对齐误差，那么融合并不会解决表现力下降的问题，IconVSR通过Coupled-Propagation来解决。
2. Alignment基于flow-based，但是为了便于缓解校正(对齐之后一般会加上CNN层，来做进一步校正或者也可以看成是feature到image的重建)因为运动估计(DCN做的是隐式的运动估计，即offset)的不精确造成输出上的artifacts，作者在BasicVSR中采用feature-wise级上的对齐。但其本质还是基于光流，因此在特征上warp的时候，只是从一个位置上根据光流来获取输出像素，因此如果光流估计出现问题，那么即使减缓了artifacts，可是这种较弱的探索性能或限制输出的表现力，特别是在遮挡问题上，DCN这种flow-free会在特征warp的时候考虑一个局部范围(卷积核大小)内的所有信息，最后输出像素，故他的探索能力更强，会为遮挡物体提供更多的细节来对齐，比如下图所示(VSR中，flow-based对齐一般都是基于TSTN来做的，比如VESPCN、Robust-LTD等；而flow-free是基于TDCN来做的，比如TDAN、EDVR等)：
   
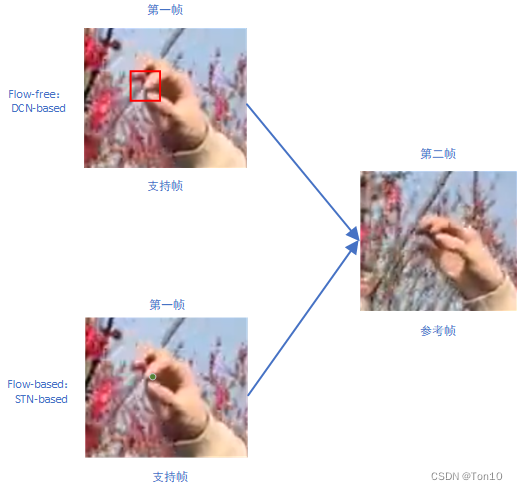
   光流法只会从支持帧中的1个位置(绿色点)中取值输出来作为参考帧的对齐帧，但是由于树枝被手遮挡了，无法获取树枝的信息，所以树枝在对齐后的输出其实就变成了手，这是和树不相关的像素值，这样就会出现对齐出错；而flow-free的方法面对遮挡问题，他会考虑一个卷积核(红色框)范围内的特征信息，最后树枝输出的对齐结果多多少少会和红色框内未遮挡的树枝有关，虽然这种对齐不完全精确，但是总比flow-free取和树枝完全不想关的手要好。因此flow-based对齐方法在遮挡问题上并不鲁棒！
3. BasicVSR在融合部分还是简单的concat合并，但IconVSR引入information-refill来将后向分支的特征信息和前向对齐的特征信息进行融合，有效解决了遮挡、边界、多细节场景问题。
4. BasicVSR和IconVSR的上采样部分都是使用残差块堆积加上亚像素卷积层来做的。

$BasicVSR\&IconVSR\&BasicVSR++$
在Propagation部分，IconVSR引入Coupled-Propagation来对BasicVSR做改进；接下来BasicVSR在IconVSR基础上进一步引入Grid-Propagation和Second-order grid propagation做改进。
在Alignment部分，BasicVSR和IconVSR一样，而BasicVSR++进一步引入flow-guided deformable alignment来做改进。
在Aggregation部分，BasicVSR++和BasicVSR一样没做改进，故并没有使用information-refill。
在Upsampling部分，三者基本一样的。

接下来我们具体分析BasicVSR++的3个$创新点$：

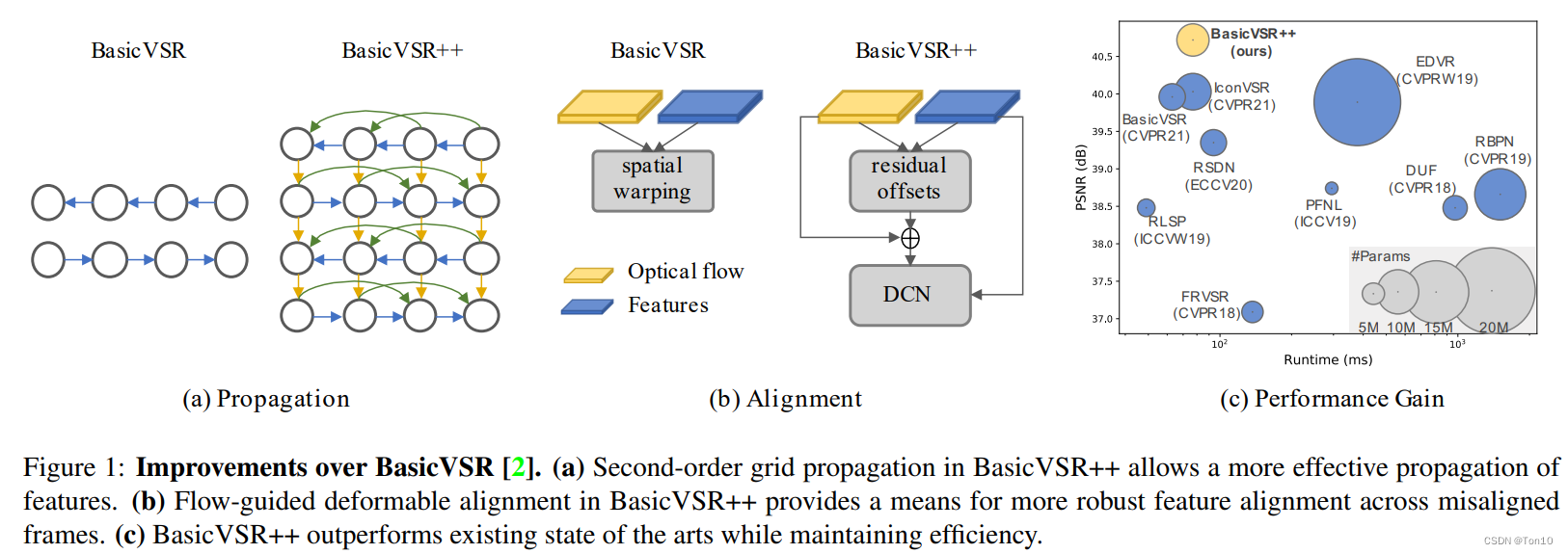
1. $Grid-Propagation$：在BasicVSR中设置了一对前向和后向分支，为了实现从粗到细的对齐，作者又多设置了一对前向和后向分支(如上图(a)中蓝色线)。此外，吸取Coupled-Propagation中后向分支将$h$传送给前向分支的思想，作者在此设计中直接添加了前向和后向之间的双向联系(如上图(a)中黄色线)来解决遮挡以及边界问题。
2. $Second-order?grid?propagation$：为了利用更久之前或未来的对齐特征信息，比如它们的位置信息，BasicVSR++引入类似于skip connection的结构(如上图(a)绿色线)，或者也可以理解为引入二阶马尔可夫特性。这种方式规避了不断对齐所造成的对较远或未来对齐特征的衰减，从而使得当前帧对齐的时候可以额外获取更多空间位置特征。这种机制对于解决边界问题和另一种遮挡问题也很有帮助。
3. $Flow-guided?deformable?alignment$：无论对齐基于feature-wise还是image-wise，反正是光流方法就会产生高度依赖于运动估计精确性问题，虽然flow-free方法也会依赖于offset的精确度，但是由于flow-free有较强的探索能力，其最后warp的结果不只取决于1个像素的运动信息(比如下图所示为flow-based对齐：
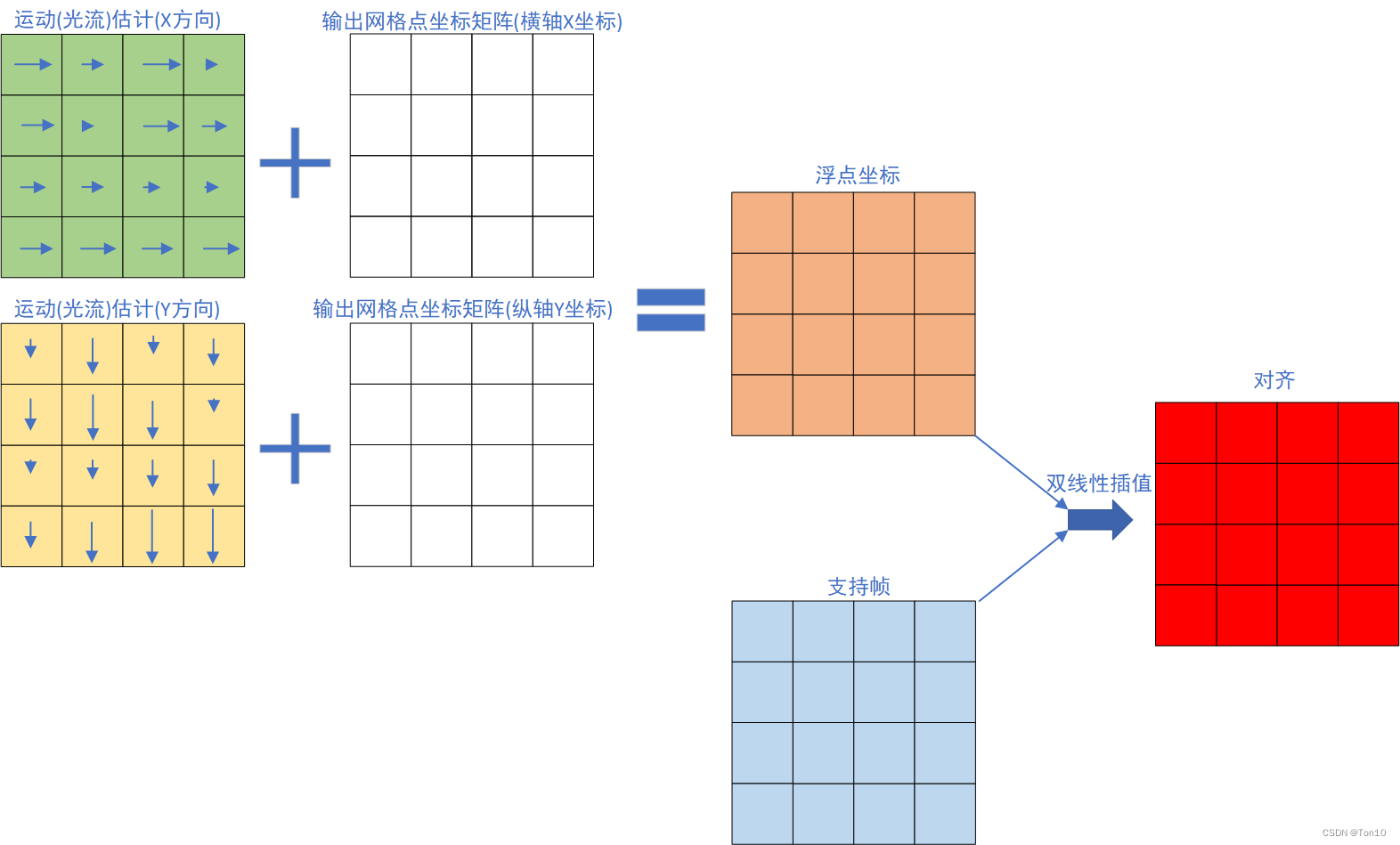
   它每个位置的对齐都只取决于1个运动矢量(flow)，简单粗暴但有明显局限性)，而是一个范围(卷积核大小)内的综合情况，其相对容错率较低所以对不会高度依赖于offset的精确性。因此BasicVSR++中，作者将对齐模块建立在基于DCN的flow-free方法上，但由于DCN较难训练，故作者还使用了flow-based来做个粗糙的特征对齐去学习offset，这个光流将和offset的学习构成残差结构来迫使网络去学习残差信息，从而减轻了直接学习offset的训练压力。也就是说并不是直接去学习offset，而是用一个flow-based对齐来引导DCN中offset的学习(如上图(b)所示)！
4. 上述3点就是BasicVSR++的创新点，需要注意的是，它只针对Propagation和Alignment做了加强，此外DCN部分借鉴了2019年的DCN-v2结构来进一步增强网络的空间变换能力。BasicVSR系列采用了简单高效的结构来解决遮挡、边界等问题以及利用了较大范围的输入特征信息。尤其是BasicVSR++，在和BasicVSR相似的模型参属下，取得了$\pm 0.82dB$的提升。关于PSNR表现力以及模型运行时间见上图?所示。

2 Related Work

略

3 Methodology

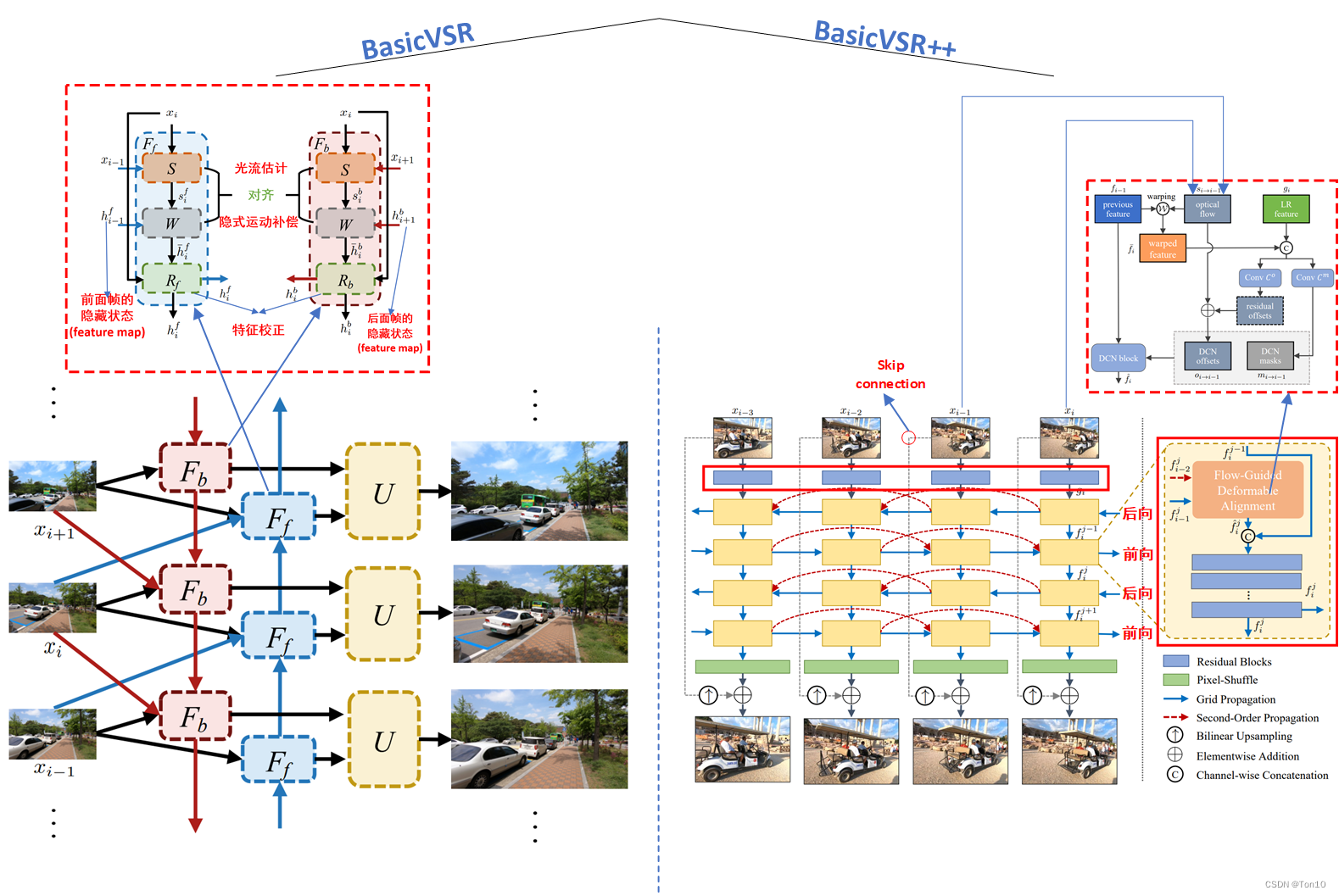
上图是BasicVSR和BasicVSR++的对比：

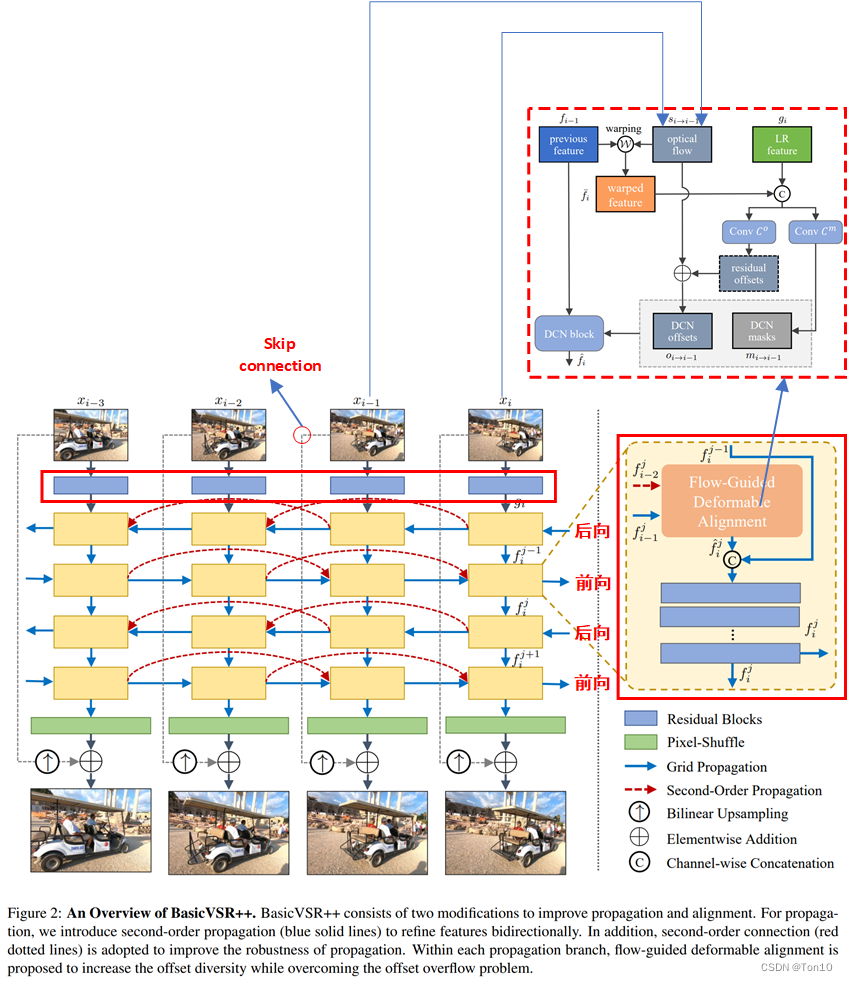
1. Propagation部分：①BasicVSR++增加了image之后的特征提取层，由一系列残差块组成；②增加了Second-Order Propagation和前后向之间的Grid-Propagation；③增了又一对的前后向分支；④增加了skip connection来将原始特征信息直接输送到高层和上采样之后的结果相结合。
2. Alignment部分：将flow-based的feature-wise对齐方式更新为flow-guided deformable alignment。

这里$skip?connection$的作用：

1. 由于从输入到输出这个过程有许多卷积层，势必会损失很多特征信息，超分的过程其实在输入和输出的差距很小，超分的目的也只是补充额外的细节信息，因此直接从输入端输送原始特征到输出端也是很有必要的。
2. 将原始信息经过双线性插值之后可以作为一种正则化项来训练主网络，故主网络可作为残差部分来训练，可增加网络训练的稳定性，这种做法在DCSCN、DRCN、EDVR等都有体现。

3.1 Second-Order Grid Propagation

二阶格点传播(SOGP)可分为格点传播(GP)和二阶传播(SOP)两小部分。

$Grid?Propagation$

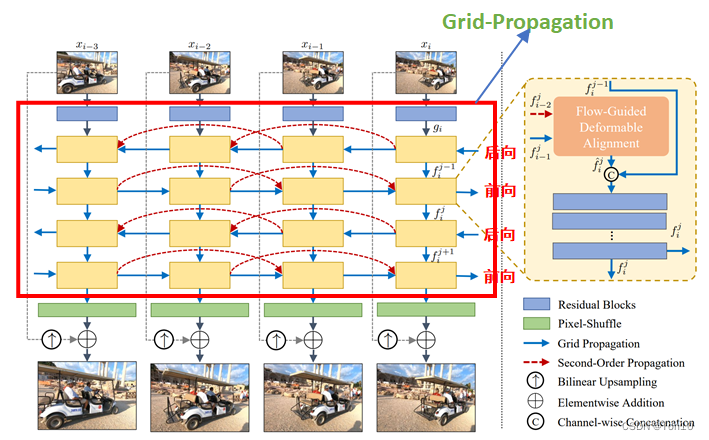
BasicVSR++的整体框架结构长得像格子状，这是因为作者增加了Grid Propagation机制。简单来说格点传播机制就是在BasicVSR基础上增多增加几对前后向分支，并结合IconVSR中Coupled-Propagation机制，在前后向之间建立联系，也就是说不仅仅只是后向输送对齐特征到前向中，Grid-Propagation还将前向输送到后向中去。这样不仅可以解决遮挡问题，还可以有效处理边界情景问题：
①对于边界问题：因为前向特征信息可以为后向提供其并不拥有的边界信息，而这一边界信息在前向特征中是一定有的，边界的特征对齐可以通过这种方式得到补充，这就类似于IconVSR的information-refill机制，但Grid-Propagation处理的更加简单高效，因为它不需要额外增加一个额外的特征提取模块(IconVSR通过一个EDVR来做的，占有了一定的模型量)。关于边界问题具体如下图所示：

②对于遮挡问题：这就和IconVSR一样了，将后向分支的信息传到前向中去，来使得前向在对齐的时候，可以有相关的像素可以得到补充，具体如下所示：
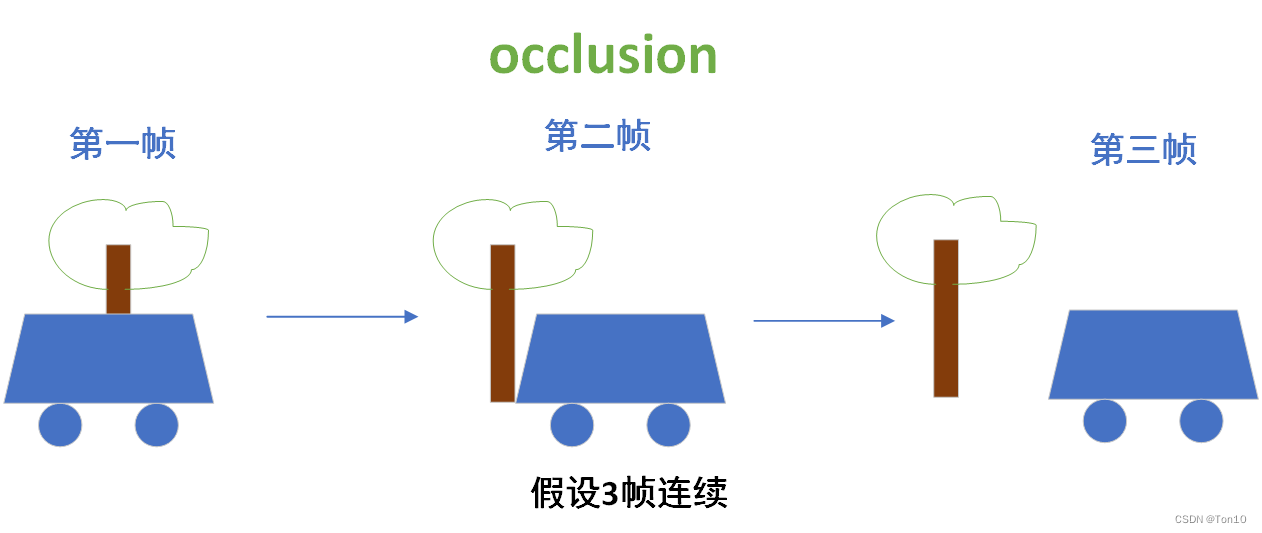当第一帧对齐第二帧的时候，如果有了后向分支中未来帧(比如上图中的第三帧)的特征信息，就可以在第一帧对齐的时候使用，因为本身第一帧是没有树干的信息的，通过后向和前向的连接之后，前向分支在对齐的时候就能更好的处理。

Note：

1. 前后向互相建连接是Grid-Propagation的核心，连接是将隐藏状态输送到块中的对齐之后特征校正之前的融合阶段。
2. Grid Propagation通过重复设置前后项分支来实现coarse-to-fine的对齐，来不断优化，减少特征信息在长序列中传播的累积误差。IconVSR通过information-refill来处理，但每次处理过于稀疏，所以对误差的减少效果是欠缺的。

$Second-Order?Propagation$

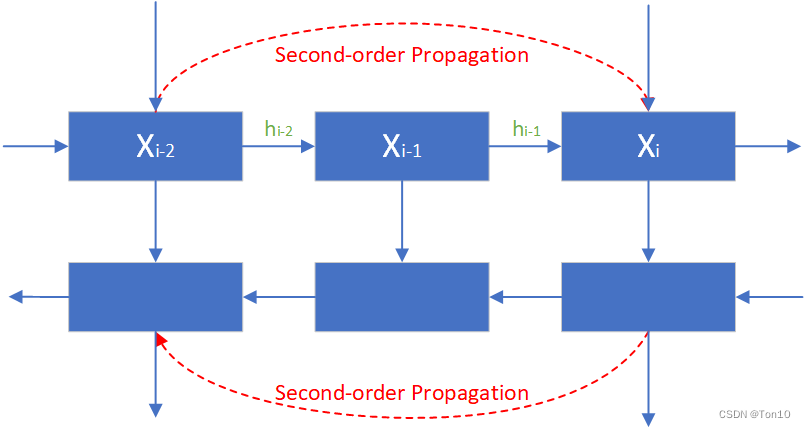
个人认为SOP其实就是个对齐块之间的skip connection，作者将其理解为是一个二阶马尔科夫链的过程，主要是因为如上图所示，当前帧的对齐除了接受上一个块的对齐特征$h_{t?1}$以外，还要接受上上个块的对齐特征$h_{t?2}$。这种跳跃连接的好处在于：

1. 它可以接受过去或未来一段时间的对齐特征信息，可以获取更多空间位置信息，而因为BasicVSR这种长距离传播机制会不断衰减过去地对齐特征，因此这种跳跃连接可以直接利用每次衰减之前的对齐特征。
2. 二阶传播也可以应对于细节区域和另一种遮挡问题。
   ①对于遮挡问题：
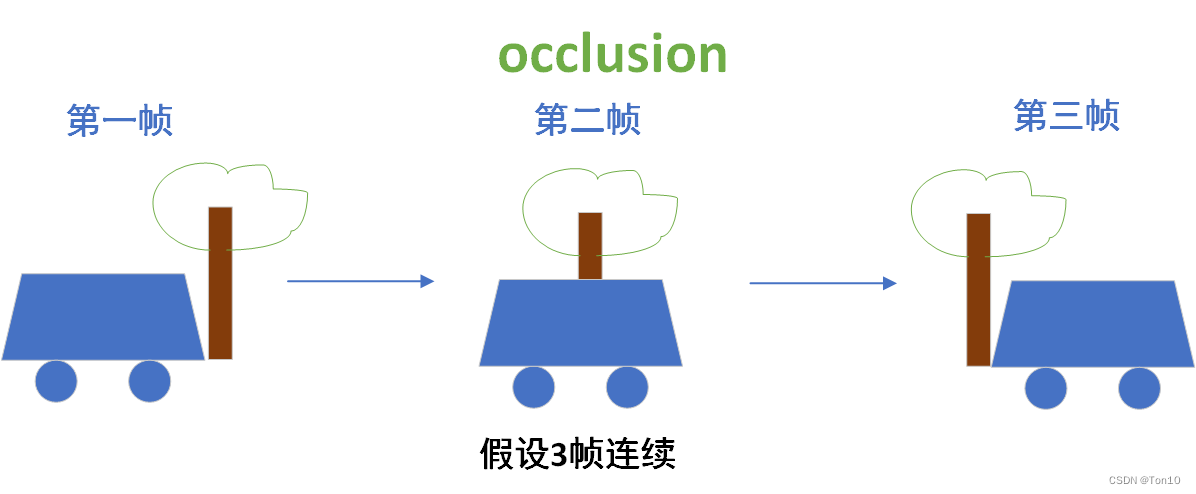   如上图所示，我们在做第二帧向第三帧对齐的时候，由于第二帧中没有第三帧中的树干信息，所以这部分就会对齐出错，而如果此次数第一帧的特征信息跨越过来，那么他就可以将树干的信息提供补充，从而完成较好的对齐。

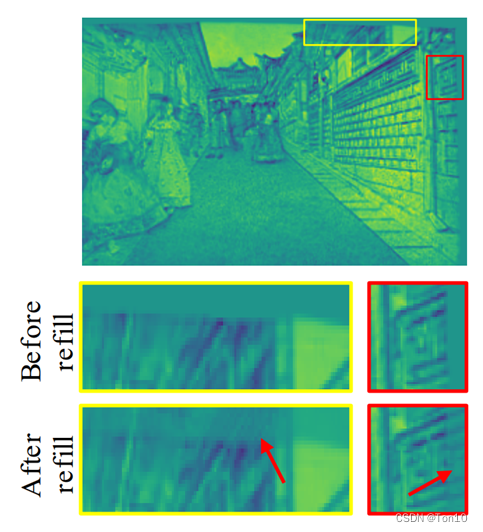
②对于细节区域：由于可以利用直接利用较远的特征信息，就可以获取更多不同的位置信息，对于细节区域的重建是很有帮助的，具体细节区域的重建效果如下所示(只是举个大致例子，并不是真的BasicVSR++的效果)：

将上述2部分结合之后就是Second-Order Grid Propagation，接下来我们用数学表达式来分析整个前向过程(后向也是同样的原理分析，只是输入流的方向改变了)：
设$x_i$表示第$i$个时间步的输入image；$g_i$代表第$i$个时间步对输入image做特征提取的feature map；$f_i^j$表示第$i$个时间步、第$j$个分支(正向和反向是一起计数的)的对齐且校正过的feature map，特别的$f_i^0=g_i$，则前向分支中每个格点的表达式为：
$$\begin{gathered} s_{i\to i?1},s_{i\to i?2}=\mathcal{S}(x_i,x_{i?1}),\mathcal{S}(x_i,x_{i?2}), \\ {\hat{f}}_i^j=\mathcal{A}?g_i,f_{i?1}^j,f_{i?2}^j,s_{i\to i?1},s_{i\to i?2}?.\text{\hspace{1em}(1)} \end{gathered}$$其中${\hat{f}}_i^j$表示经过flow-guided deformable alignment之后对齐feature map，它包含了$i?1,i?2$时间步之前所有的对齐信息，当然有一定程度的衰减；$s_{i\to i?1},s_{i\to i?2}$分别表示第$i$帧到第$i?1,i?2$帧的光流；算子$\mathcal{S}(?)$表示光流估计，在BasicVSR和BasicVSR++中都使用SPyNet完成，它更加简单和高效(VESPCN中的光流估计使用一些简单CNN的堆叠)。接着我们将来自后向分支的对齐feature map拿过来进行concat，然后再送进特征校正模块中改善一下，具体表达式为：
$$f_i^j={\hat{f}}_i^j+\mathcal{R}?c(f_i^{j?1},{\hat{f}}_i^j)?.\text{\hspace{1em}(2)}$$
Note：

1. $c(?,?)$表示concat，$\mathcal{R}(?)$表示堆积的残差块。
2. 最后通过相加(图中未画出)是为了结合对齐特征，补充因残差块的卷积层而造成一些特征信息的损失。

3.2 Flow-Guided Deformable Alignment

上面提到过，flow-free对齐方法，比如TDCN可以不高度依赖于光流估计的准确性，因为其探索能力较强，最终的输出不仅仅取决于1个点的偏移；其次DCN对齐方法对于遮挡情景所展现的重建效果也越好，故BasicVSR++决定采用基于flow-free的DCN来做对齐，但是DCN的训练很难，过程中较不稳定，故作者通过额外的flow-based对齐来引导DCN中offset的学习，接下来我们介绍整个对齐过程$\mathcal{A}$，和SOGP一样，我们只介绍前向对齐过程，且为了便于讨论，只分析单个分支，故忽略分支计数符号$j$，整个对齐模块内部框图如下：

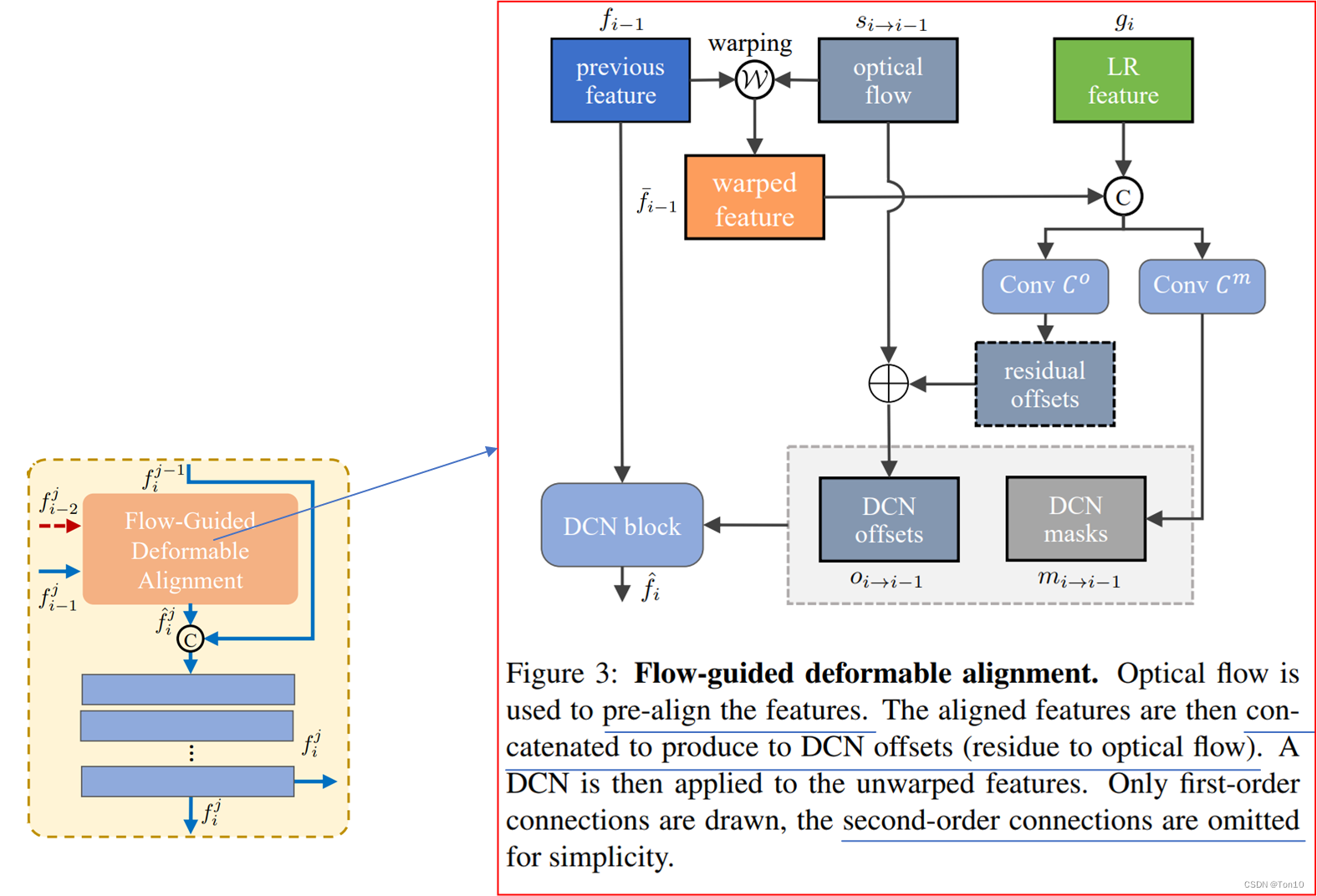
在正式介绍之前，我们需要明白为何可以用光流来引导offset的学习？
在这篇文章Understanding Deformable Alignment in Video Super-Resolution中揭示了DCN-based对齐和flow-based对齐之间的强相关性，DCN中的每一个offset都和光流有着高度的相似性，但存在着微小的差别，它们之间的shape大致都类似，可能只是预测的运动方向不同，而DCN最终在每一个位置warp的结果是多个offsets的总和，他们之间的关系如下所示(只是大致描述，offsets表示最终1个卷积核内所有offsets)：

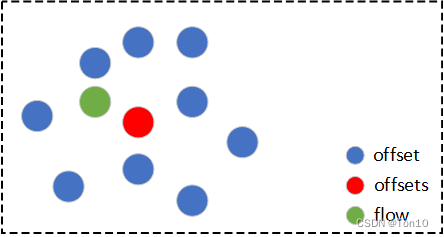
有了这一层关系在，我们只要限定offsets在事先计算好的光流周围，或者说让它两的距离很靠近，这样的话offset就不会溢出，其训练的稳定性也会大大增加。限定这种情况大致有2种方法：①像Understanding Deformable Alignment in Video Super-Resolution这篇文章中那样，设置offset-fidelity损失函数最小化flow和每个offset的距离；②像本文中BasicVSR++那样，通过设置残差结构来减轻offsets的训练压力。
Note：

1. 关于更多关于offset-fidelity损失函数的细节可参考我的另一篇论文笔记之Understanding Deformable Alignment in Video Super-Resolution。

$一、一阶传播下的对齐$
①首先是一次预对齐过程：
$${\bar{f}}_{i?1}=\mathcal{W}(f_{i?1},s_{i\to i?1}).\text{\hspace{1em}(3)}$$$\mathcal{W}(?)$做的就是BasicVSR做的对齐，采用flow-based但基于feature-wise的对齐方式；$s_{i\to i?1}$表示第$i$帧对第$i?1$帧的光流；${\bar{f}}_{i?1}$表示和$x_i$对齐的feature map(本质是STN类方法warp可以在image或者feature map上均可)，我们可以将这个过程理解为一次粗糙的对齐。

②然后我们要利用光流对齐的结果${\bar{f}}_{i?1}$和光流$s_{i\to i?1}$来引导DCN中offset和modulated scalars的学习：
$$\begin{gathered} o_{i\to i?1}=\stackrel{residual}{s_{i\to i?1}+\underset{offset}{{\mathcal{C}}^o?c(g_i,{\bar{f}}_{i?1})?}}, \\ {m}_{i\to i?1}=\sigma ?\underset{modulatedscalars}{{\mathcal{C}}^m?c(g_i,{\bar{f}}_{i?1})?}?.\text{\hspace{1em}(4)} \end{gathered}$$Note：

1. $c(?,?)$表示合并concat的过程。
2. $c(g_i,{\bar{f}}_{i?1})$表示将分别代表第$i$帧特征和第$i?1$帧特征进行合并，这和TDAN、EDVR中的相邻帧合并是一样的。
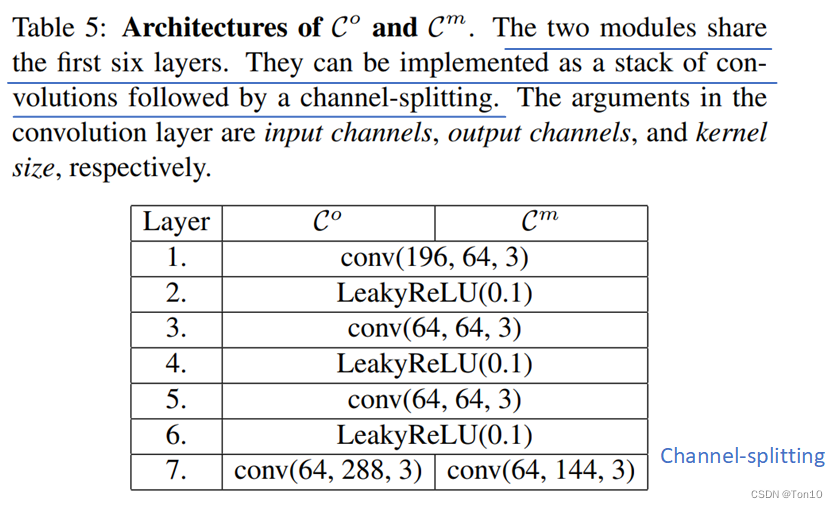
3. ${\mathcal{C}}^o?c(g_i,{\bar{f}}_{i?1})?、{\mathcal{C}}^m?c(g_i,{\bar{f}}_{i?1})?$表示常规学习DCN-v2中偏移参数和调制常数参数的过程，他们都表示CNN层的堆积，实验中具体如下：因为可变形卷节分组$G=16$，而每一组学习的offset张数为$2N$张，modulation masks为$N$张，在实验中$N=3^2$，即可变形卷积核大小的平方倍。因此对于offset，最后输出的通道数为$16\times 2\times 9=288$，而modulation masks为$16\times 9=144$张feature map。
   ；$o_{i\to i?1}、m_{i\to i?1}$分别表示offsets和modulation masks。
4. $\sigma (?)$表示sigmoid函数，用于将调制参数控制在$[0,1]$。
5. 和常规学习offset不一样的是，BasicVSR++并不直接学习offset，而是先学习残差offset，而最终的offset是来自基于残差和光流$s_{i\to i?1}$的和。这么做的好处在于，我们只要学习残差信息${\mathcal{C}}^o?c(g_i,{\bar{f}}_{i?1})?$即可，因为最终学得的offsets具有和光流$s_{i\to i?1}$相似的性质，因此残差部分的offset只是1个很小的值(具有较小的波动范围)，而学习1个较小的值相对而言会更加容易，其方差会小很多，训练的稳定性自然会增加；换句话说，在已经存在光流的基础上，只需要学习1个很小的值进行微调即可，这就是为何残差结构可以充当offset-fidelity的角色来稳定offset的训练的原因。
6. 额外补充下，对于光流，光流估计网络每次产生$G\times 2$张feature map，而DCN每次产生$G\times 2N$张feature map，这也和Understanding Deformable Alignment in VSR这篇文章中论述光流相当于$N=1$时候的可变形卷积相呼应。

③最后进行DCN过程，可以看成是一次精细的对齐：
$${\hat{f}}_i=\mathcal{D}(f_{i?1};o_{i\to i?1},m_{i\to i?1}).\text{\hspace{1em}(5)}$$

$二、二阶传播下的对齐$
因为存在二阶传播，因此一种简单的想法就是分别做2次一阶对齐，即对$f_{i?1}、f_{i?2}$都做一次上面的过程，但是显然这样非常消耗计算资源，并且其实$f_{i?1}、f_{i?2}$是相关的，它们的对齐过程可以互相帮助。所以一个直观的做法就是将3帧一起合并来学习2个offsets和modulation masks。具体过程如下：
①首先预对齐还是分开来各做各的，光流$s_{i\to i?1}、s_{i\to i?2}$和一阶对齐一样都来自于现成的光流估计网络SPyNet：
$$\begin{gathered} {\bar{f}}_{i?1}=\mathcal{W}(f_{i?1},s_{i\to i?1}), \\ {\bar{f}}_{i?2}=\mathcal{W}(f_{i?2},s_{i\to i?2}). \end{gathered}$$
②然后我们要利用光流对齐的结果${\bar{f}}_{i?1},{\bar{f}}_{i?2}$和光流$s_{i\to i?1},s_{i\to i?2}$来引导DCN中offset和modulated scalars的学习，通过将3帧一起合并来学习2个offsets和modulation masks：
$$\begin{gathered} o_{i\to i?p}=s_{i\to i?p}+{\mathcal{C}}^o?c(g_i,{\bar{f}}_{i?1},{\bar{f}}_{i?2})?, \\ {m}_{i\to i?p}=\sigma ?{\mathcal{C}}^m?c(g_i,{\bar{f}}_{i?1},{\bar{f}}_{i?2})??.\text{\hspace{1em}(6)} \end{gathered}$$其中$p=1,2$。
Note：

1. 实际上，在残差内的offsets和modulation masks的学习都是共享的。

③接下去，我们要将学习到的offsets和modulation masks进行合并，产生最终用于DCN的offsets($o_i$)和modulation masks($m_i$)，最终warp的对象也是$f_{i?1}、f_{i?2}$的合并：
$$\begin{gathered} o_i=c(o_{i\to i?1},o_{i\to i?2}), \\ {m}_i=c(m_{i\to i?1},m_{i\to i?2}), \\ {\hat{f}}_i=\mathcal{D}(c(f_{i?1},f_{i?2});o_i,m_i).\text{\hspace{1em}(7)} \end{gathered}$$
通过上述这种在对齐中引入残差结构来构造出光流引导的offset学习，来克服DCN训练不稳定以及offset容易溢出的问题，这样做主要有3个好处：

1. 传统DCN学习offsets是通过CNN来做的，但CNN只能利用图像空间的局部区域，因此其学得的offset只能反应局部区域的运动，这就造成了其会产生次优对齐，因此通过与使用光流进行预对齐之后的feature上进行学习offset将会变得更加准确，可以理解为有了预对齐之后，一些大运动问题就会变成小运动问题，这样就会使得offset可以在卷积的局部采样上发挥作用(个人认为预对齐可以看成是一种粗糙的对齐)。
2. 由于最终的offset和光流信号十分接近，因此残差部分只是个很小的值，整个对齐网络只需要去学习这个小幅度变动的残差网络，即offset和modulation masks。小幅度变化的值更容易去学，其方差更小，这样就减轻了直接学习offset的压力，增加了DCN训练的稳定性，缓解过拟合。
3. BasicVSR++对齐中的DCN采用DCN-v2版本，因为其中包含modulation mask，其可以控制offset的幅度来使得新采样点可以移动到合适的位置，其本质是一种注意力机制，他会让DCN更加关注能使对齐性能提升的采样位置。

4 Experiments

$数据集$
验证集：REDSval4，即REDS数据集中Clips 000,001,006,017。
测试集：REDS4，即REDS数据集中Clips 000,011,015,020；Vid4；UDM10；Vimeo-90K-T。
训练集：REDS中除了REDS4和REDSval4之外的视频数据；Vimeo-90K。
采用4倍下采样获取$LR$视频，下采样方法为经典的BI和BD。

$实验设置$

1. Adam、CA做优化；loss函数使用charbonnier函数。
2. 主网络和光流估计网络的学习率分别为$10^{?4},2.5\times 10^{?5}$。
3. 总共的迭代次数为60W次；且前5000次迭代中光流估计网络的参数固定不动。
4. Patch为$48\times 48$。
5. Batch=8，每个batch包含连续30帧$LR$图像，由于Vimeo-90K只有连续7帧，无法捕捉长序列信息，因此当训练在Vimeo数据集上，就使用REDS上的训练参数作为初始化参数，并微调30W个iterations。此外，测试的时候是全序列输入。
6. 光流估计使用SPyNet网络。
7. 每个分支中使用7个残差块，且每个块的输出通道设置为64。
8. 特征提取层的残差块设置为5。
9. DCN的可变形卷积核大小为$3\times 3$，且可变形卷积分组$G=16$。

4.1 Comparisions with State-of-the-Art Methods

作者首先将BasicVSR++和其余16种模型相对比，实验结果如下：

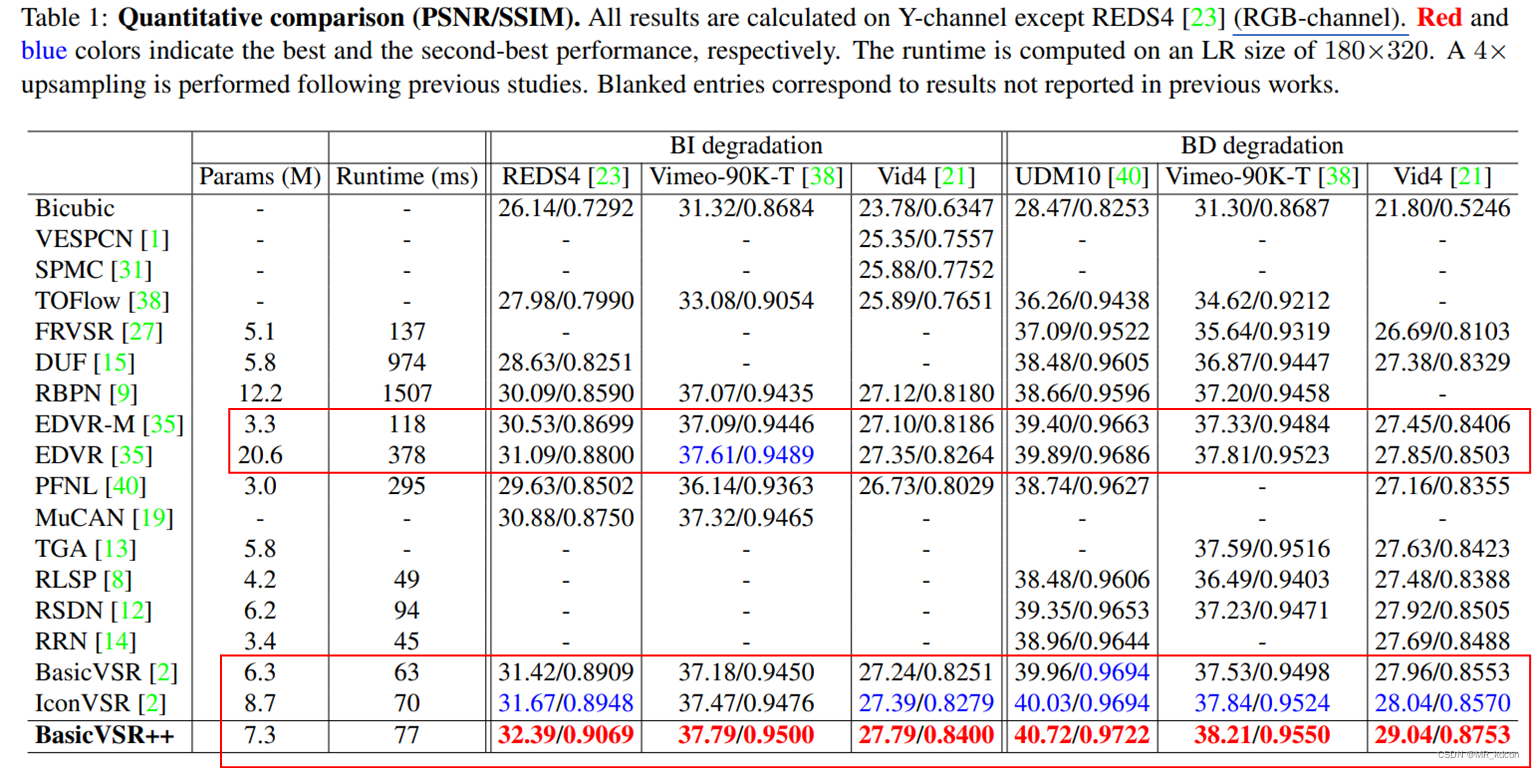
实验结论：

1. EDVR是sliding-window模式下的一种高表现力VSR方法，但是BasicVSR++在参数量比它少了很多的情况下保持PSNR的提升为$1.3dB$。
2. BasicVSR++在保持参数量和BasicVSR、IconVSR类似的情况下，取得了SOTA的表现力，也证明了BasicVSR++是BasicVSR的加强版本。
3. 作者还训练了一个轻量版本的BasicVSR++，它和BasicVSR、IconVSR的性能对比如下：

在测试集上的可视化结果如下：

5 Ablation Studies

本节作者探究2个提升点各自的功能。
首先放上SOGP和flow-guided deformable alignment(FGDA)对重建性能的影响：

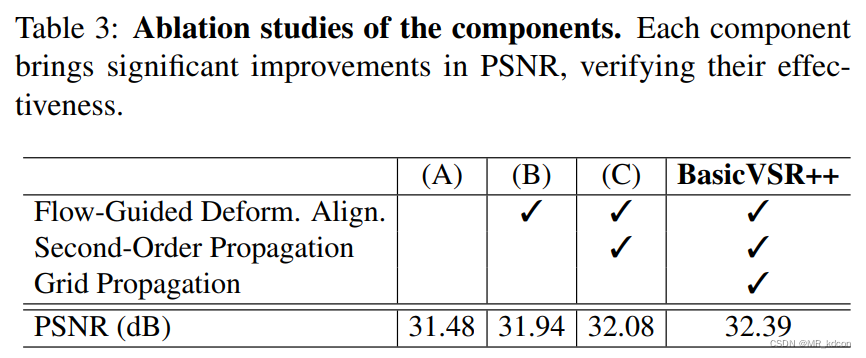
实验结论：

1. 每一个成分的增加都是的PSNR得到了提升，说明了二阶传播(SOP)、两次传播迭代(GP)以及光流引导的可变形对齐都有助于VSR性能提升。
2. 作者指出，增加传播的阶数或者传播迭代数目并不会进一步提高太多VSR的性能(仅仅$0.05dB$)，因此保持二阶和2对前后项分支是折中的一种最佳选择。

接下来我们具体分析2个提升点的作用。

$SOGP$
实验结果如下：

从图中可以看出SOGP对于多细节区域的重建表现是很不错的。这是因为GP的多迭代传播可以产生从粗到细的对齐；此外SOP的二阶传播可以融合集聚多个帧的相关对齐特征信息，他们提供了丰富的位置信息，这些信息互为补充来产生更加精确的对齐，为细节区域的重建提供了帮助。

$FGDA$
实验一：实验结果如下所示：

上图(a)是(e)(f)之间的光流信息；(b)~(d)是$G\times 2\times N=288$张offset特征图中任取的3张；(g)是光流对齐的结果；(h)是使用本文提出的FGDA对齐的结果。
实验结论：

1. 和我们上述分析的一样，最终学习到的每一个offsets(对应每一张偏移feature map)都和光流flow大致形状一样，只是存在微小的差别，此外不同的offset在预测方向上也有差别。从这里也可以看出为何DCN探索性更强，因为flow-based对齐中1个位置的warp只取决于该位置对应的1个光流信号，因此其高度依赖于运动估计的准确性，一旦不够精确，就会出现artifacts；而DCN在1个位置的warp取决于多个flow-like共同聚合的综合结果，不同的offset可以互相提供补充的运动信息。这种较强的探索能力在遮挡、边界这种看不见的或不存在的区域的对齐上效果显著，此外这种多个offset共同决定warp的特性产生的方差更小，故可以有效减少大运动下的对齐误差。
2. 从(g)(h)的可视化中可以看出，flow-based产生了较模糊的边缘；而FGDA由于聚合了多样的运动信息，故最后产生的对齐feature map就能产生不错的效果，如(h)中细节区域就很清晰。

实验二：
设置一组对比试验，3种设置分别是：①没有光流，纯DCN对齐；②将光流只用于损失函数种，即offset-fidelity损失函数；③光流引导的DCN对齐，即本文的FGDA。实验结果如下所示：

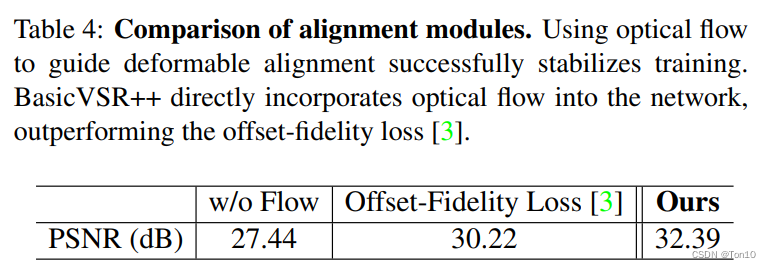
实验结论如下：

1. 从上图可知，有光流的参与使得PSNR的值分别提升了$2.78dB,4.95dB$，证明了光流引导DCN学习的有效性。
2. 本文提出的FGDA基于残差来用光流引导DCN的学习比只有将光流用在损失函数中的方法提升了$2.17dB$，证明了FGDA是一种更好的引导方式。

$Temporal?Consistency$
时间连续性也是VSR中一个重要的方向。在基于sliding-windows方法中，比如EDVR，不同输出的重建都是独立的；而在基于循环结构的方法中，比如BasicVSR、BasicVSR++，通过中间特征的不断传播，使得不同的输出之间是相互关联的，这种内在联系使得输出是连续的。相关实验结果如下：

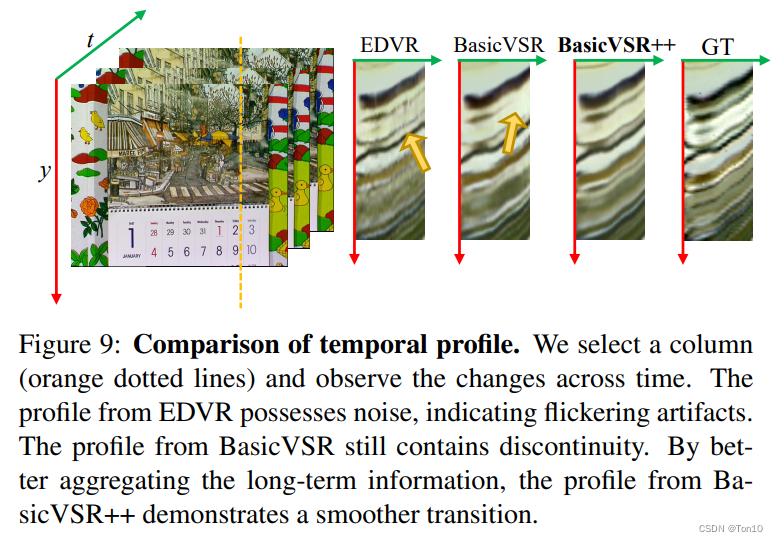
显然，基于循环机制的方法能产生更好的连续性；此外，BasicVSR++比BasicVSR产生更加平滑的时间传播连续性。

运动(光流)估计和DCN的offset具有很高的相似性，他们都表征了运动信号，只不过后者是通过隐式的捕捉这种运动信号。

6 NTIRE 2021 Challenge Results

BasicVSR++在2021年的超分挑战赛获得了2项冠军，其表现力可视化如下：

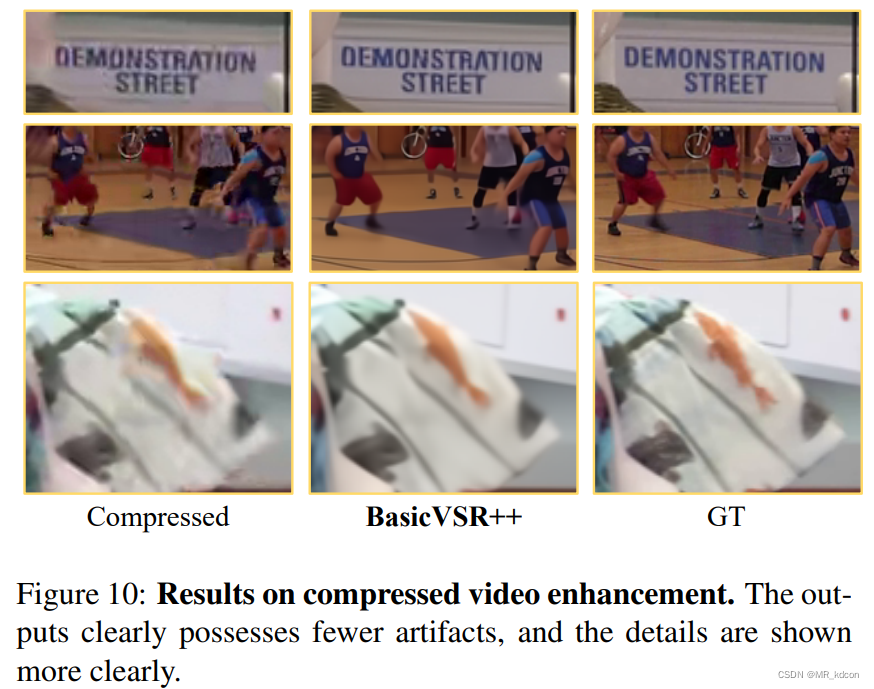
7 Conclusion

1. BasicVSR++基于BasicVSR，在其结构上对Propagation和Alignment部分进行了提升改进，分别使用了Second-order grid propagation和Flow-guided deformable alignment技术。
2. Second-order grid propagation分为Grid propagation和Second-order propagation两部分，分别增加了前后想分支的迭代数目以及基于二阶马尔可夫假设设置了接受前后项2帧的对齐特征。
3. Flow-guided deformable alignment使用了光流引导的DCN中offset的学习，这种方式以DCN为主对齐网络，以flow-based对齐为预对齐网络。通过预对齐网络来训练offset，同时让光流和offset构成残差结构输出最终用于可变形卷积的offset，需要注意的是这个offset并不是直接学习得到的，而是通过光流引导的残差结构学习到的。这种方式可以稳定DCN的训练，减缓offset的溢出。
4. 通过以上2个成分的提升，BasicVSR++以较少的模型参数量达到了SOTA的表现力！

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖