2022/5/10日
Generalized Label Enhancement with Sample Correlations
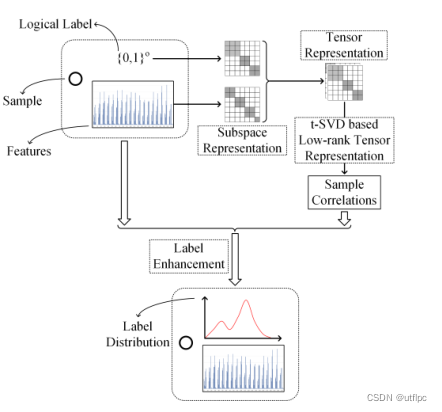
可以实现样本特征和现有逻辑标签的底层样本相关性来监督标签分布的整个恢复过程,从而实现LE的细化,并充分利用数据样本的隐含信息。
目标函数
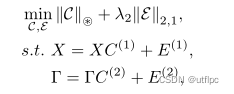
基于t-SVD的张量核范数
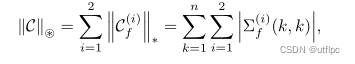
∥
C
f
(
i
)
∥
\big\Vert \mathcal{C}_f^{(i)} \big\Vert
∥∥?Cf(i)?∥∥?表示沿
C
\mathcal{C}
C的第 3 维进行的快速傅立叶变换 (FFT),即
C
\mathcal{C}
C的正面切片
Z. Zhang, G. Ely, S. Aeron, N. Hao, and M. Kilmer, “Novel methods for multilinear data completion and de-noising based on tensor-svd,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2014, pp. 3842–3849.
根据矩阵核范数的酉不变性,
∥
C
∥
?
\big\Vert \mathcal{C} \big\Vert_\circledast
∥∥?C∥∥???可转化为:
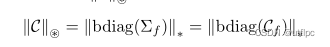
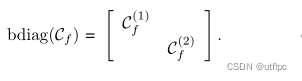
2022/5/11日
Generalized Label Enhancement with Sample Correlations
mapping model 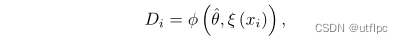
基于t-SVD的张量核范数 ∥ C ∥ ? \big\Vert \mathcal{C} \big\Vert_\circledast ∥∥?C∥∥???转变为:
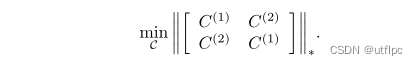
通过使用基于t-SVD的低秩张量约束,可以将逻辑标签的底层信息以及特征空间中的信息纳入样本相关性的形成过程。
augmented Lagrange multiplier (ALM) approach
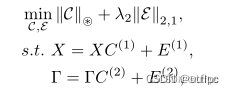
目标函数的最小化问题采用增强拉格朗日乘数 (ALM) 方法解决
目标函数得到优化并获得所需的样本相关性后,便可实现标签分布的精确恢复过程:
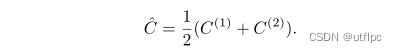
θ \theta θ的目标函数

该目标函数的最小化将通过 limited memory BFGS (L-BFGS)得到.
