文章目录
九、卷积神经网络(CNN)
卷积神经网络(ConvolutionalNeuralNetwork,CNN)是一种深度前馈神经网络,目前在图片分类、图片检索、目标检测、目标分割、目标跟踪、视频分类、姿态估计等图像视频相关领域中已有很多较为成功的应用。
9.1 全连接层
拉平为一个列向量
全连接层(Fully Connected Layer)可以简单地理解为前面章节中提到的神经网络的一个隐藏层,它包含权重向量W和激活函数。
具体来说,对于一张
32
?
32
?
3
32*32*3
32?32?3的图片(宽和高均为32个像素,有RGB三个通道,可以将其理解为一个的
32
?
32
?
3
32*32*3
32?32?3矩阵),要通过全连接层,首先要将其拉伸为3072*1的向量作为神经网络隐藏层的输入,然后该向量与权重向量W做点乘操作,再将点乘后的结果作为激活函数(如Sigmoid或tanh)的输入,最终,激活函数输出的结果便是全连接层的最终结果。操作过程如图所示,其中activation中蓝色圆圈的值表示所有3072个输入和10维权重向量W点乘的结果。

当完成激活(activation)后的结果为一维向量时,通常将该结果称为特征向量(或激活向量);当激活后的结果为二维向量时,通常称为特征层(feature map,有时也称为激活层,activation map)。由于后面要介绍的卷积层也需要经过激活函数,因此卷积操作得到的结果通常被称为“特征层”。
9.2 卷积层
卷积运算:两矩阵对应元素相乘相加得到的值
卷积层(Convolution Layer)与全连接层不同,它保留了输入图像的空间特征,即对于一张 32 ? 32 ? 3 32*32*3 32?32?3的图片而言,卷积层的输入就是的 32 ? 32 ? 3 32*32*3 32?32?3矩阵,不需要做任何改变。在卷积层中,我们引入了一个新的概念:卷积核kernel(常简称为卷积,有时也称为滤波器filter)。卷积的大小可以在实际需要时自定义其长和宽(常见的卷积神经网络中通常将其设置为 1 ? 1 、 3 ? 3 、 5 ? 5 1*1、3*3、5*5 1?1、3?3、5?5等),其通道个数一般设置为与输入图片通道数量一致。
必要的概念已经介绍完毕,接下来我们讲一下卷积的过程:让卷积(核)在输入图片上依次进行滑动,滑动方向为从左到右,从上到下;每滑动一次,卷积(核)就与其滑窗位置对应的输入图片x做一次点积计算并得到一个数值。
这里需要提到另外一个概念:步长(stride)。步长是指卷积在输入图片上移动时需要移动的像素数,如步长为1时,卷积每次只移动1个像素,计算过程不会跳过任何一个像素,而步长为2时,卷积每次移动2个像素。
9.2.1 一维卷积
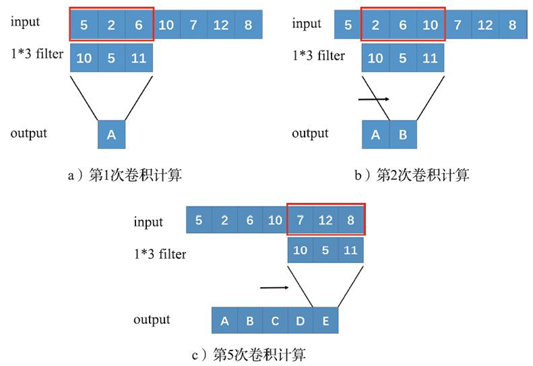
为方便大家理解,我们先来看一下一维卷积的情况,如图a所示,输入是一个
1
?
7
1*7
1?7维的向量及其对应的数值,我们定义一维卷积,其卷积大小为
1
?
3
1*3
1?3(数值分别为“10,5,11”),那么经过第一次卷积操作(卷积与其对应的输入做点积)后我们可以得到
10
?
5
+
5
?
2
+
11
?
6
=
126
10*5+5*2+11*6=126
10?5+5?2+11?6=126,所以这里的A对应的数值即为126。在这个例子里,我们定义步长为1,所以接下来卷积移动一个格子(在图像中一个步长可以理解为一个像素),如图b所示,可以计算得到B的数值为160。以此类推,最终得到一个
1
?
5
1*5
1?5维的向量。
卷积每次滑动覆盖的格子范围在图像处理中被称为“感受野”,这个名词在后文中还会用到。图中所示的“感受野”为
1
?
3
1*3
1?3。
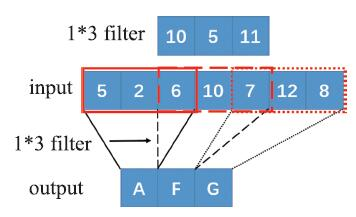
接下来,我们可以扩展到如图8-3所示的步长为2的情况,同样是 1 ? 7 1*7 1?7的输入向量,每次移动两个格子,即卷积从“5, 2,6”移动到“6,10,7”,然后再移动到“7,12,8”,完成所有的卷积操作之后(与步长为1不同),这里最终将得到一个 1 ? 3 1*3 1?3的向量。
9.2.2 二维卷积
看完了一维卷积的计算之后,我们再来学习下二维卷积的计算。对于一个 7 ? 7 7*7 7?7的图片,我们定义一个 3 ? 3 3*3 3?3的卷积,步长分别为1和2,读者可以先自行思考一下其计算过程,如果你已经想好了,请参考前图和下图,看与你的想法是否一致。我们可以看出,步长为1时,输出的特征层(feature map,有时也称为激活层activation map)大小为 5 ? 5 5*5 5?5,而步长为2时,则为 3 ? 3 3*3 3?3。那么,当步长为3时,输出的卷积层大小是多少呢?答案是:会有错误,对于一个 7 ? 7 7*7 7?7的图片不能使用步长为3的 3 ? 3 3*3 3?3卷积。(做卷积的时候必须要涉及到全部的元素)
- 步长为1
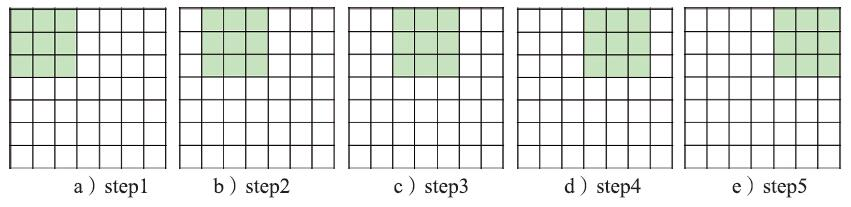
- 步长为2
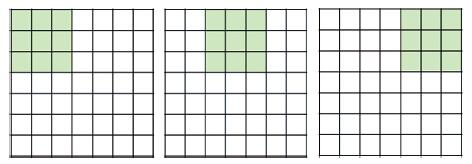
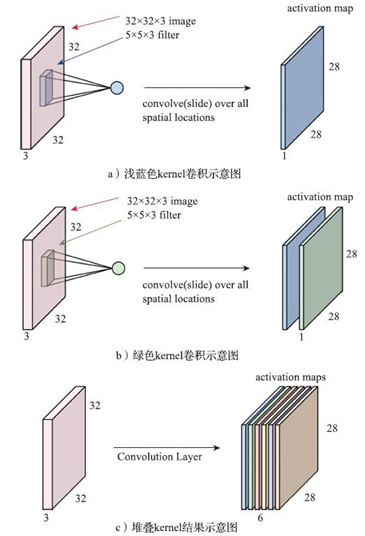
图c的步长为1
如图a所示,输入为一张 32 ? 32 ? 3 32*32*3 32?32?3的图,kernel大小为 5 ? 5 ? 3 5*5*3 5?5?3(这里的感受野为 3 ? 3 3*3 3?3),那么每一次滑动都将带来卷积和输入图片 5 ? 5 ? 3 = 75 5*5*3=75 5?5?3=75点乘的计算量,完成整个图片的卷积后最终将生成一张 28 ? 28 ? 1 28*28*1 28?28?1的新图片b),即特征层(feature map)。类似地,我们再定义一个卷积(通常可以理解为不同卷积完成不同的任务),这时特征层将产生2个通道。接下来,我们连续堆叠6个不同的卷积(kerne/filter)结果,最终特征层将得到6个通道,而这就可以理解为一张 28 ? 28 ? 6 28*28*6 28?28?6的新图片(如图c)。
9.2.3 卷积神经网络
介绍完了卷积层,接下来我们看看什么是卷积神经网络。如下图所示,卷积神经网络是由一系列卷积层经过激活来得到的。接下来我们看一种更为通用的卷积形式,在
7
?
7
7*7
7?7的输入图片周边做1个像素的填充(pad=1),如右图所示,步长为1,kernel为
3
?
3
3*3
3?3的卷积输出的特征层将为
7
?
7
7*7
7?7。我们在这里给出通用卷积层的计算公式:输入图像为
W
1
?
H
1
?
D
1
W1*H1*D1
W1?H1?D1(字母分别表示图像的宽、高、channel),卷积层的参数中kernel大小为
F
?
F
F*F
F?F,步长为S,pad大小为P,kernel个数为K,那么经过卷积后,输出图像的宽、高、channel分别为:
W
2
=
W
1
?
F
+
2
P
S
+
1
H
2
=
H
1
?
F
?
2
P
S
+
1
D
2
=
K
W_2 = \frac{W_1 - F + 2P}{S} + 1 \\ H_2 = \frac{H_1 - F - 2P}{S} + 1 \\ D_2 = K
W2?=SW1??F+2P?+1H2?=SH1??F?2P?+1D2?=K
接下来看一个例子
- 输入为 32 ? 32 ? 3 32*32*3 32?32?3
- kernel个数为10,大小为 5 ? 5 5*5 5?5
- 步长为1
- pad为2
那么根据以上计算公式可以得出
(
32
?
5
+
2
?
2
)
/
1
+
1
=
32
(32-5+2*2)/1+1=32
(32?5+2?2)/1+1=32,因此我们可以得知输出的特征层大小为
32
?
32
?
10
32*32*10
32?32?10。与此同时,我们也可以得到每个kernel对应的参数个数
5
?
5
?
3
+
1
=
76
5*5*3+1=76
5?5?3+1=76(+1表示bias),因此该层卷积最终的参数个数为
76
?
10
=
760
76*10=760
76?10=760
至此,卷积层的基本运算已介绍完毕,那么卷积层的参数是如何与第7章介绍的传统神经网络参数对应的呢?实际上,卷积层学习的关键就是几个kernel。在上例中,
76
?
10
=
760
76*10=760
76?10=760
可以对应到传统神经网络中的w0~wn,而输入x1~xn则是输入图片。与传统神经网络不同的是,卷积层的计算是含有空间信息的。
9.3 池化层
池化层对原始特征层的信息进行压缩
9.3.1 池化(pooling)
池化(pooling)是对图片进行压缩(降采样)的一种方法,池化的方法有很多,如(网格里面求最大值)max pooling、(求网格的平均值)average pooling等。池化层也有操作参数,我们假设输入图像为
W
1
?
H
1
?
D
1
W1*H1*D1
W1?H1?D1(字母分别表示图像的宽、高、channel),池化层的参数中,池化kernel的大小为F*F,步长为S,那么经过池化后输出的图像的宽、高、channel分别为:
W
2
=
W
1
?
F
S
+
1
H
2
=
H
1
?
F
S
+
1
D
2
=
K
W_2 = \frac{W_1 - F}{S} + 1 \\ H_2 = \frac{H_1 - F}{S} + 1 \\ D_2 = K
W2?=SW1??F?+1H2?=SH1??F?+1D2?=K
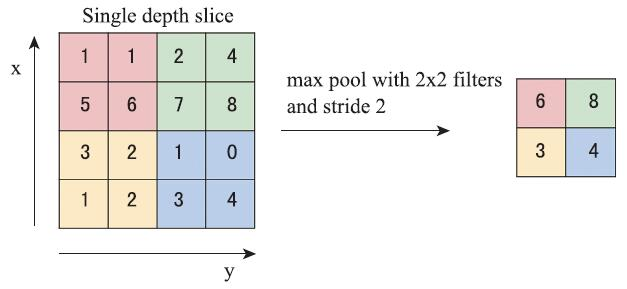
通常情况下F=2,S=2。如上图所示,一个 4 ? 4 4*4 4?4的特征层经过池化filter= 2 ? 2 2*2 2?2,stride=2的最大池化操作后可以得到一个 2 ? 2 2*2 2?2的特征层。
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self): #在这里定义卷积神经网络需要的元素
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5) #定义第一个卷积层
self.pool = nn.MaxPool2d(2, 2) #池化层
self.conv2 = nn.Conv2d(6, 16, 5) #定义第二个卷积层
self.fc1 = nn.Linear(16 * 5 * 5, 120) #全连接层
self.fc2 = nn.Linear(120, 84) #全连接层
self.fc3 = nn.Linear(84, 10) #最后一个全连接层用作10分类
def forward(self, x): #使用__init__中的定义,构建卷积神经网络结构
x = self.pool(F.relu(self.conv1(x))) #第一个卷积层首先要经过relu做激活,然后使用前面定义好的nn.MaxPool2d(2, 2)方法做池化
x = self.pool(F.relu(self.conv2(x))) #第二个卷积层也要经过relu做激活,然后使用前面定义好的nn.MaxPool2d(2, 2)方法做池化
x = x.view(-1, 16 * 5 * 5) #对特征层tensor维度进行变换
x = F.relu(self.fc1(x)) #卷积神经网络的特征层经过第一次全连接层操作,然后再通过relu层激活
x = F.relu(self.fc2(x)) #卷积神经网络的特征层经过第二次全连接层操作,然后再通过relu层激活
x = self.fc3(x) #卷积神经网络的特征层经过最后一次全连接层操作,得到最终要分类的结果(10类标签)
return x
net = Net()
9.4 批规范层
避免过拟合
让学习的过程早一点结束
批规范化层(BatchNorm层)是2015年Ioffe和Szegedy等人提出的想法,主要是为了加速神经网络的收敛过程以及提高训练过程中的稳定性。虽然深度学习被证明有效,但它的训练过程始终需要经过精心调试,比如精心设置初始化参数、使用较小的学习率等。Ioffe和Szegedy等人进行了详细的分析,并给出了BatchNorm方法,在后面的很多实验中该方法均被证明非常有效(8.2.4节中介绍的ResNet就在重复使用该结构)。这里首先介绍一下batch的概念:在使用卷积神经网络处理图像数据时,往往是几张图片(如32张、64张、128张等)被同时输入到网络中一起进行前向计算,误差也是将该batch中所有图片的误差累计起来一起回传。BatchNorm方法其实就是对一个batch中的数据根据公式(8-1)做了归一化。
x
^
k
=
x
k
?
E
[
x
k
]
V
a
r
(
x
k
)
\widehat{x}_k = \frac{x_k - E[x_k]}{\sqrt{Var(x_k)}}
x
k?=Var(xk?)?xk??E[xk?]?
… 一些常见卷积神经网络结构
9.6 VGG16实现Cifar10分类
########################################
#第1步:载入数据
########################################
import torch
import torchvision
import torchvision.transforms as transforms
#使用torchvision可以很方便地下载cifar10数据集,而torchvision下载的数据集为[0, 1]的PILImage格式,我们需要将张量Tensor归一化到[-1, 1]
transform = transforms.Compose(
[transforms.ToTensor(), #将PILImage转换为张量
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))] #将[0, 1]归一化到[-1, 1]
)
trainset = torchvision.datasets.CIFAR10(root='./book/classifier_cifar10/data', #root表示cifar10的数据存放目录,使用torchvision可直接下载cifar10数据集,也可直接在https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz这里下载(链接来自cifar10官网)
train=True,
download=True,
transform=transform #按照上面定义的transform格式转换下载的数据
)
trainloader = torch.utils.data.DataLoader(trainset,
batch_size=4, #每个batch载入的图片数量,默认为1
shuffle=True,
num_workers=2 #载入训练数据所需的子任务数
)
testset = torchvision.datasets.CIFAR10(root='./book/classifier_cifar10/data',
train=False,
download=True,
transform=transform)
testloader = torch.utils.data.DataLoader(testset,
batch_size=4,
shuffle=False,
num_workers=2)
cifar10_classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
########################################
#查看训练数据
#备注:该部分代码可以不放入主函数
########################################
# import numpy as np
# dataiter = iter(trainloader) #随机从训练数据中取一些数据
# images, labels = dataiter.next()
# images.shape #(4L, 3L, 32L, 32L)
# #我们可以看到images的shape是4*3*32*32,原因是上面载入训练数据trainloader时一个batch里面有4张图片
# torchvision.utils.save_image(images[1],"test.jpg") #我们仅随机保存images中的一张图片看看
# cifar10_classes[labels[j]] #打印label
########################################
#第2步:构建卷积神经网络
########################################
import math
import torch
import torch.nn as nn
import os
cfg = {'VGG16':[64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M']}
class VGG(nn.Module):
def __init__(self, net_name):
super(VGG, self).__init__()
#构建网络的卷积层和池化层,最终输出命名features,原因是通常认为经过这些操作的输出为包含图像空间信息的特征层
self.features = self._make_layers(cfg[net_name])
#构建卷积层之后的全连接层以及分类器
self.classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(512, 512), #fc1
nn.ReLU(True),
nn.Dropout(),
nn.Linear(512, 512), #fc2
nn.ReLU(True),
nn.Linear(512, 10), #fc3,最终cifar10的输出是10类
)
#初始化权重
for m in self.modules():
if isinstance(m, nn.Conv2d):
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, math.sqrt(2. / n))
m.bias.data.zero_()
def forward(self, x):
x = self.features(x) #前向传播的时候先经过卷积层和池化层
x = x.view(x.size(0), -1)
x = self.classifier(x) #再将features(得到网络输出的特征层)的结果拼接到分类器上
return x
def _make_layers(self, cfg):
layers = []
in_channels = 3
for v in cfg:
if v == 'M':
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
else:
#conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
#layers += [conv2d, nn.ReLU(inplace=True)]
layers += [nn.Conv2d(in_channels, v, kernel_size=3, padding=1),
nn.BatchNorm2d(v),
nn.ReLU(inplace=True)]
in_channels = v
return nn.Sequential(*layers)
net = VGG('VGG16')
########################################
#第3步:定义损失函数和优化方法
########################################
import torch.optim as optim
#x = torch.randn(2,3,32,32)
#y = net(x)
#print(y.size())
criterion = nn.CrossEntropyLoss() #定义损失函数:交叉熵
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9) #定义优化方法:随机梯度下降
########################################
#第4步:卷积神经网络的训练
########################################
for epoch in range(5): #训练数据集的迭代次数,这里cifar10数据集将迭代2次
train_loss = 0.0
for batch_idx, data in enumerate(trainloader, 0):
#初始化
inputs, labels = data #获取数据
optimizer.zero_grad() #先将梯度置为0
#优化过程
outputs = net(inputs) #将数据输入到网络,得到第一轮网络前向传播的预测结果outputs
loss = criterion(outputs, labels) #预测结果outputs和labels通过之前定义的交叉熵计算损失
loss.backward() #误差反向传播
optimizer.step() #随机梯度下降方法(之前定义)优化权重
#查看网络训练状态
train_loss += loss.item()
if batch_idx % 2000 == 1999: #每迭代2000个batch打印看一次当前网络收敛情况
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, train_loss / 2000))
train_loss = 0.0
print('Saving epoch %d model ...' % (epoch + 1))
state = {
'net': net.state_dict(),
'epoch': epoch + 1,
}
if not os.path.isdir('checkpoint'):
os.mkdir('checkpoint')
torch.save(state, './checkpoint/cifar10_epoch_%d.ckpt' % (epoch + 1))
print('Finished Training')
- 测试
########################################
#第5步:批量计算整个测试集预测效果
########################################
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item() #当标记的label种类和预测的种类一致时认为正确,并计数
print('Accuracy of the network on the 10000 test images: %d %%' % (100 * correct / total))
#结果打印:Accuracy of the network on the 10000 test images: 73 %
########################################
#分别查看每个类的预测效果
########################################
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %2d %%' % (
cifar10_classes[i], 100 * class_correct[i] / class_total[i]))
