Transformer Quality in Linear Time

????????本文提出一种新型高效(速度,内存,效果)的注意力方法,依然具有N^2的复杂度(N:同一个 attention 中词向量的个数)。对比:(a) An augmented Transformer layer which consists of two blocks: Gated Linear Unit (GLU) and Multi-Head Self-Attention (MHSA), (b) Our proposed Gated Attention Unit (GAU), ? Pseudocode for Gated Attention Unit. Skip connection and input normalization over the residual branch are omitted in (a), (b) for brevity.
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import einsum
class GAU(nn.Module):
def __init__(
self,
dim,
query_key_dim = 128,
expansion_factor = 2.,
add_residual = True,
dropout = 0.,
):
super().__init__()
hidden_dim = int(expansion_factor * dim)
self.norm = nn.LayerNorm(dim)
self.dropout = nn.Dropout(dropout)
self.to_hidden = nn.Sequential(
nn.Linear(dim, hidden_dim * 2),
nn.SiLU()
)
self.to_qk = nn.Sequential(
nn.Linear(dim, query_key_dim),
nn.SiLU()
)
self.gamma = nn.Parameter(torch.ones(2, query_key_dim))
self.beta = nn.Parameter(torch.zeros(2, query_key_dim))
nn.init.normal_(self.gamma, std=0.02)
self.to_out = nn.Sequential(
nn.Linear(hidden_dim, dim),
nn.Dropout(dropout)
)
self.add_residual = add_residual
def forward(self, x):
seq_len = x.shape[-2]
normed_x = self.norm(x) #(bs,seq_len,dim)
v, gate = self.to_hidden(normed_x).chunk(2, dim = -1) #(bs,seq_len,seq_len)
Z = self.to_qk(normed_x) #(bs,seq_len,query_key_dim)
QK = einsum('... d, h d -> ... h d', Z, self.gamma) + self.beta
q, k = QK.unbind(dim=-2)
sim = einsum('b i d, b j d -> b i j', q, k) / seq_len
# 注:原文提到\mathcal Q and \mathcal K are two cheap transformations that apply per-dim scalars and offsets to Z
# 本代码的放缩因子为n
A = F.relu(sim) ** 2
A = self.dropout(A)
V = einsum('b i j, b j d -> b i d', A, v)
V = V * gate
out = self.to_out(V)
if self.add_residual:
out = out + x
return out
gau = GAU(
dim = 512, # nn.LayerNorm(dim) 对[*, 512]进行norm
query_key_dim = 128, # query / key dimension
expansion_factor = 2, # hidden dimension = dim * expansion_factor
)
x = torch.randn(1, 1024, 512)
out = gau(x) # (1, 1024, 512)
Vanilla MLP
O = ? ( X W u ) W o X ∈ R n × d , W u ∈ R d × e , W o ∈ R e × d \boldsymbol{O}=\phi(\boldsymbol{X}\boldsymbol{W}_u)\boldsymbol{W}_o\\ \boldsymbol{X}\in\mathbb{R}^{n\times d},\boldsymbol{W}_u\in\mathbb{R}^{d\times e},\boldsymbol{W}_o\in\mathbb{R}^{e\times d} O=?(XWu?)Wo?X∈Rn×d,Wu?∈Rd×e,Wo?∈Re×d
Gated Linear Unit (GLU)
U = ? u ( X W u ) , V = ? v ( X W v ) ∈ R T × e O = ( U ⊙ V ) W o ?????????????????????????? ∈ R T × d \quad \boldsymbol{U}=\phi_u(\boldsymbol{X}\boldsymbol{W}_u), \quad\boldsymbol{V}=\phi_v(\boldsymbol{X}\boldsymbol{W}_v) \in \mathbb{R}^{T\times e}\\ \boldsymbol{O}=(\boldsymbol{U}\odot\boldsymbol{V})\boldsymbol{W}_o \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \in \mathbb{R}^{T\times d} U=?u?(XWu?),V=?v?(XWv?)∈RT×eO=(U⊙V)Wo???????????????????????????∈RT×d
Gated Attention Unit (GAU)
Z = ? z ( X W z ) ?????????????????????????? ∈ R T × s A = 1 n relu 2 ( Q ( Z ) K ( Z ) ? s ) = 1 n s relu 2 ( Q ( Z ) K ( Z ) ? ) , ∈ R T × T \boldsymbol{Z}=\phi_z(\boldsymbol{X}\boldsymbol{W}_z) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \in \mathbb{R}^{T\times s} \\ \boldsymbol{A}=\frac{1}{n}\text{relu}^2\left(\frac{\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}}{\sqrt{s}}\right)=\frac{1}{ns}\text{relu}^2\left(\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}\right),\in \mathbb{R}^{T\times T} Z=?z?(XWz?)??????????????????????????∈RT×sA=n1?relu2(s?Q(Z)K(Z)??)=ns1?relu2(Q(Z)K(Z)?),∈RT×T
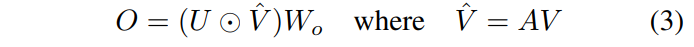
????????论文还给出了Pseudocode For FLASH-Quad and FLASH的几种试验。
https://arxiv.org/pdf/2202.10447.pdf
FLASH:可能是近来最有意思的高效Transformer设计
门控注意力单元(GAU)还需要Warmup吗?
6种注意力的数学原理和代码实现:ProbSparse Attention LogSparse Attention LSH Attention Sparse Attention Single-Headed Attention
