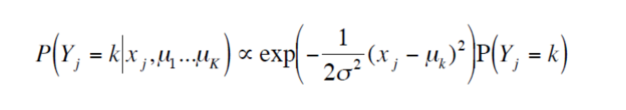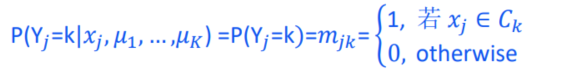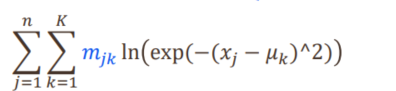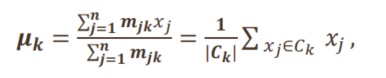[人工智能][机器学习入门]——第七课——非监督聚类

第七课——非监督聚类

非监督学习

监督学习=通过对有限的标记数据学习决策函数𝑓，从而预测未见样本的标签

非（无）监督学习=通过对原始未标记的数据学习，来揭示数据的内在性质及规律

1?? 考虑发掘数据的纵向结构， 把相似的样本聚到同簇，即对数据进行聚类

2?? 考虑发掘数据的横向结构，把高维空间的向量转化为低维空间的向量，即对数据进行降维

3?? 考虑数据的纵向与横向结构，假设数据由含有隐式结构的概率模型生成，从数据中学习该概率模型

使用无标注数据 X = { x 1 , x 2 , . . . , x N } X=\{x_1,x_2,...,x_N\} X={x1?,x2?,...,xN?} 学习或训练，无监督学习的模型是函数$z=g_{\theta }(x)$或条件概率分布$P_{\theta }(z|x)$

针对聚类问题

硬聚类，每一个样本属于某一簇$z=g_{\theta }(x)$

软聚类，每一个样本以概率属于某一簇$P_{\theta }(z|x)$

针对降维问题，$z=g_{\theta }(x)$，其中𝑧𝑖 是𝑥𝑖 的低维向量，函数 𝑔 既可以是线性函数也可以是非线性函数

针对概率模型问题，假设数据由一个概率模型生成，由训练 数据学习概率模型的结构和参数。

一、聚类简介

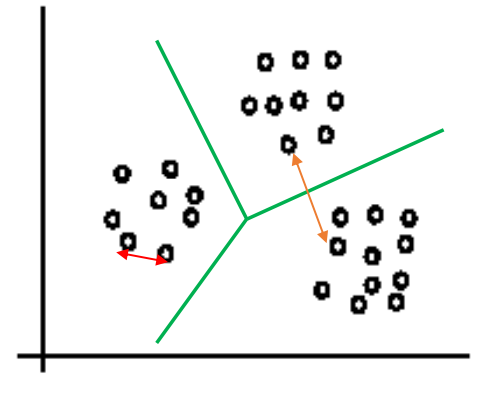
聚类clustering：聚类将同类型的样本聚为不同簇的过程

簇内距小，簇间距大：一个簇中的样本之间彼此相似，而不同簇之间的的样本不相似

无监督学习的最常见形式

聚类中的问题

簇的定义：什么是聚类对象的自然簇？

数据表示：向量空间？归一化等

“相似性/距离”：度量聚类对象之间的关系

簇的个数：事先指定？数据驱动？

聚类算法：划分聚类算法，层次聚类算法

算法的收敛性：是否收敛，收敛速度？

聚类是主观的：可以有多个聚类结果

机器学习将聚类对象转化成数值向量，从而使得相似可以通过计算距离量化

距离度量性质

• 对称性：$d(x_i,x_j)=d(x_j,x_i)$

  否则可以声称：“A和B相似，但是B和A不相似”

• 同一性：$d(x_i,x_i)=0$

  否则可以声称：“A比B更像B”

• 分离性：$d(x_i,x_j)=0当且仅当x_i=x_j$

  否则没办法将不同的目标区分开来

• 三角不等式：$d(x_i,x_j)\le d(x_i,x_k)+d(x_j,x_k)$

  否则可以声称A和C及B和C都相似，但是A和B不相似

常见距离度量

Minkowski 距离（闵氏距离）：

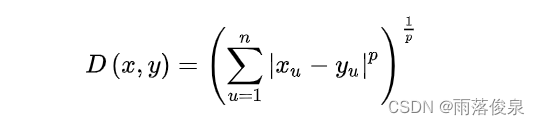
1?? 绝对距离

当p=1时，得到绝对值距离，也叫曼哈顿距离（Manhattan distance）、出租汽车距离或街区距离（city block distance）。在二维空间中可以看出，这种距离是计算两点之间的直角边距离，相当于城市中出租汽车沿城市街道拐直角前进而不能走两点连接间的最短距离。绝对值距离的特点是各特征参数以等权参与进来，所以也称等混合距离。

2?? 欧氏距离

当p=2时，得到欧几里德距离（Euclidean distance）距离，就是两点之间的直线距离（以下简称欧氏距离）。欧氏距离中各特征参数是等权的。

3?? 切比雪夫距离

令$p\to \infty$，得到切比雪夫距离——最大距离

划分式聚类

层次聚类算法

自底向上：聚合

自顶向下：分裂

划分式（ Partitional ）聚类算法

通常给出随机化初始划分

对划分进行迭代优化：K-means和GMM（高斯混合模型聚类）

给定待聚类的数据及聚类的数目K, 试图基于选定的划分准则找到数据的最佳聚类结果

理想情况：枚举所有划分

全局最优

不可行：划分可能性多达$K^n$

有效的启发式方法：k-means，k-medoids

K-means聚类法

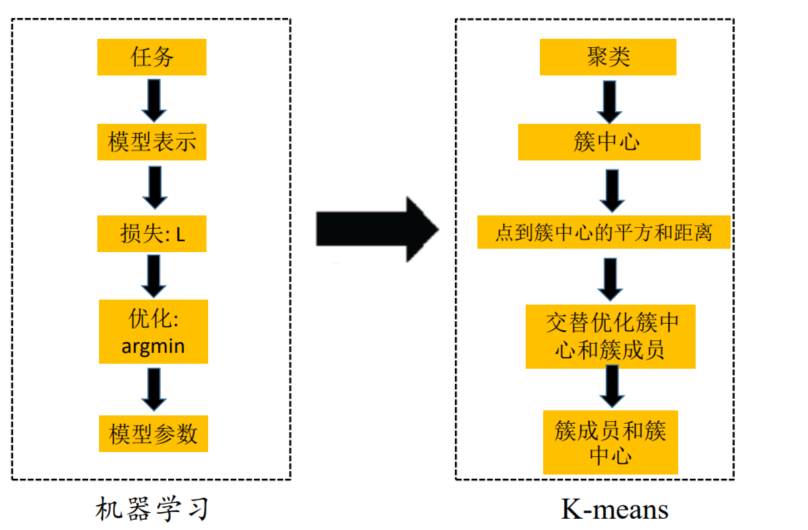
K-means是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越小，其相似度就越大。

算法步骤

📥 输入：数据 { x 1 , x 2 , … , x n } \{x_1,x_2,…,x_n\} {x1?,x2?,…,xn?}，簇的数目K

1?? 随机选择K个数据点作为簇中心 { μ 1 , μ 2 , . . . , μ K } \{\mu_1,\mu_2,...,\mu_K\} {μ1?,μ2?,...,μK?}

2?? 开始如下迭代

? 🅰? 对每个样本$x_j$进行归簇，距离哪个聚类中心最近，则将其归为哪一簇:
x j ∈ C i ? m i n t = 1 , . . . , K { ∣ ∣ x j = μ t ∣ ∣ } = ∣ ∣ x j ? μ i ∣ ∣ x_j\in C_i\Leftrightarrow \underset{t=1,...,K}{min}\{||x_j=\mu _t||\}=||x_j-\mu_i|| xj?∈Ci??t=1,...,Kmin?{∣∣xj?=μt?∣∣}=∣∣xj??μi?∣∣

? 🅱? 重新计算每个簇$C_i$的均值：${\mu }_i=\frac{1}{C_i}{\sum }_{x_j\in C_i}{x}_j$，将更新后的均值作为新的簇中心

3?? 簇中心不发生改变时中止迭代

📤 输出：簇中心 { μ 1 , μ 2 , . . . , μ K } \{\mu_1,\mu_2,...,\mu_K\} {μ1?,μ2?,...,μK?}，聚类结果 C = { C 1 , C 2 , . . . , C K } C=\{C_1,C_2,...,C_K\} C={C1?,C2?,...,CK?}

K-means的目标/损失函数

问题描述：给定无标记数据 { x 1 , x 2 , . . . , x n } \{x_1,x_2,...,x_n\} {x1?,x2?,...,xn?}，学习目标是将数据归到K个簇中： C = { C 1 , C 2 , . . . , C K } C=\{C_1,C_2,...,C_K\} C={C1?,C2?,...,CK?}，从而使得以下目标函数值最小：
$$\underset{C,\mu }{\mathrm{argmin}}\sum _{i=1}^K\sum _{x_j\in C_i}||x_j?{\mu }_i|{|}_2^2$$
希望簇内样本到簇中心的平方和距离最小，即要求簇内的样本是紧密的：这是一个非凸组合优化问题——NP hard

迭代优化

解决方法：使用迭代优化（交替优化）——固定一组，优化另一组，这个思想很重要

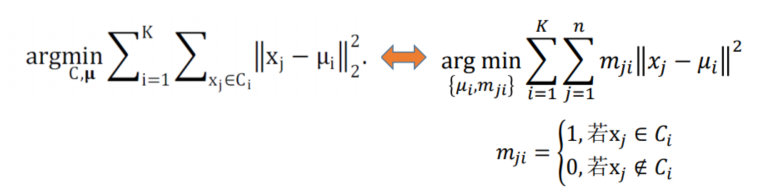
M中的m_ji项表示若第j个样本$x_j$属于第i类$C_i$则为1，否则为0，矩阵表达式如下：
$$M=?\begin{array}{cccc}{m}_{11}& m_{12}& ?& m_{1K}\\ m_{21}& m_{22}& ?& m_{2K}\\ ?& ?& ?& ?\\ m_{n1}& m_{n2}& ?& m_{nK}\end{array}?$$

使用的是硬判断

步骤：

1?? 初始化K个簇中心： { μ 1 , μ 2 , . . . , μ K } \{\mu_1,\mu_2,...,\mu_K\} {μ1?,μ2?,...,μK?}

2?? 迭代进行以下优化

更新簇成员：固定 { μ 1 , μ 2 , . . . , μ K } \{\mu_1,\mu_2,...,\mu_K\} {μ1?,μ2?,...,μK?}，优化$m_{ji}$

交换优化问题的求和顺序：
$$\min \sum _{j=1}^n\sum _{i=1}^K{m}_{ji}||x_j?{\mu }_i|{|}^2$$
由于每个样本划分簇互不影响，上式等价于对每个$x_j$，单独计算以下优化问题
min ? ∑ i = 1 K m j i ∣ ∣ x j ? μ i ∣ ∣ 2 m j i = { 1 , min ? t = 1 , . . . , K { ∣ ∣ x j ? μ t ∣ ∣ } = ∣ ∣ x j ? μ i ∣ ∣ 0 , 其 他 \min\sum_{i=1}^Km_{ji}||x_j-\mu_i||^2\\ m_{ji}=\begin{cases}1,&\min_{t=1,...,K}\{||x_j-\mu_t||\}=||x_j-\mu_i||\\ 0,&其他\end{cases} mini=1∑K?mji?∣∣xj??μi?∣∣2mji?={1,0,?mint=1,...,K?{∣∣xj??μt?∣∣}=∣∣xj??μi?∣∣其他?

更新簇中心：固定$m_{ji}$(类成员)，优化${\mu }_i$

等价于对每个簇中心${\mu }_i$，单独计算以下优化问题
$$\min \sum _{j=1}^n{m}_{ji}||x_j?{\mu }_i|{|}^2$$
令上述优化问题的梯度=0，可以得到：
$$\sum _{j=1}^n{m}_{ji}(x_j?{\mu }_i)=0?{\mu }_i=\frac{{\sum }_{j=1}^n{m}_{ji}{x}_j}{{\sum }_{j=1}^n{m}_{ji}}=\frac{1}{|C_i|}\sum _{x_j\in C_i}{x}_j$$
即在簇$C_i$中所有点$x_j$加和然后除以簇大小

算法复杂性

算法分析

聚类中心初值的选择

聚类结果依赖初值的选择：有些初值导致较差的聚类结果

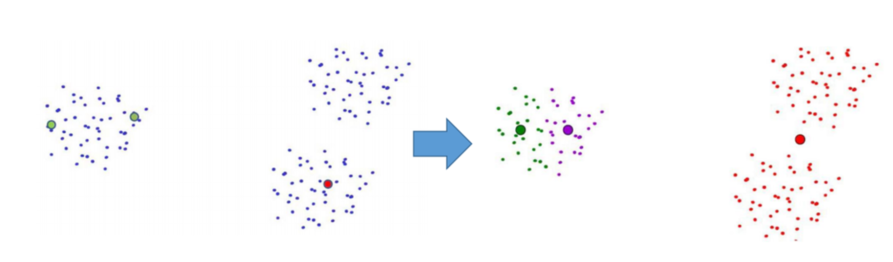
这是由于目标函数非凸导致：有多个最优解，求到的解不是全局的最优

实际中：

通过启发式方法选择好的初值：例如要求种子点之间有较大的距离

尝试多个初值，选择平方误差和最小的一组聚类结果

聚类数目K的选择

利用拐点法：目标函数的值和 k 的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的最佳聚类数。k=2时，对应肘部，故选择k值为2

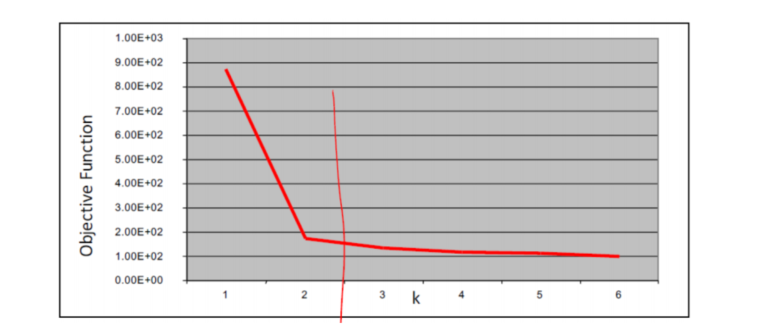
局限性

K-means不适合对形状不是超维椭圆体（或超维球体）的数据

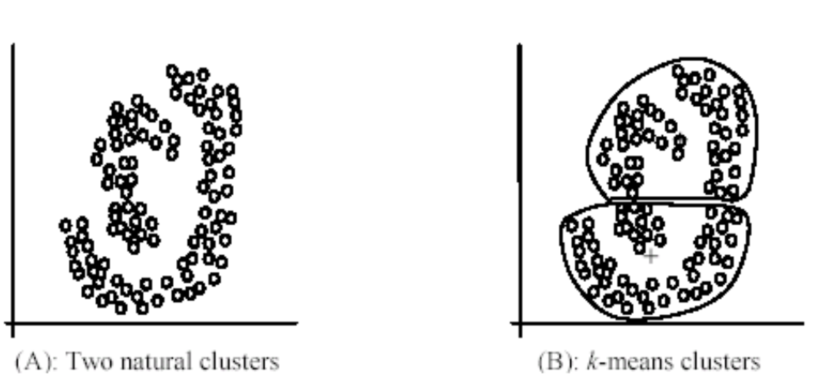
二、GMM聚类算法

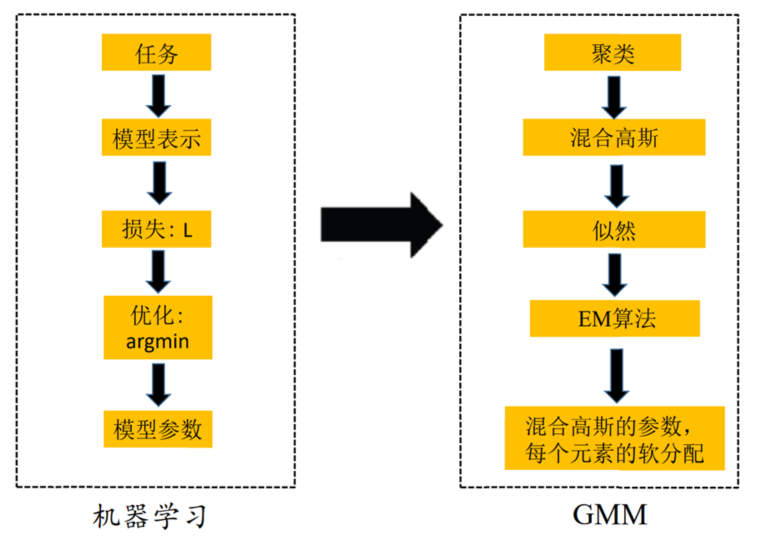
概述

K-means是判别式模型，属于硬判断，每个样本仅属于一簇

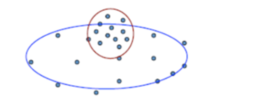
簇与簇之间有重叠区域

样本以概率属于某个簇

如何建模？

为解决以上问题，使用概率模型

允许簇与簇之间的区域重叠

有表示模型，容易泛化

属于软判断，每个样本可以属于多个簇

是生成式模型

样本由K个混合概率分布模型生成
KaTeX parse error: No such environment: align at position 8: \begin{?a?l?i?g?n?}? &P(X)=\sum_{i=…

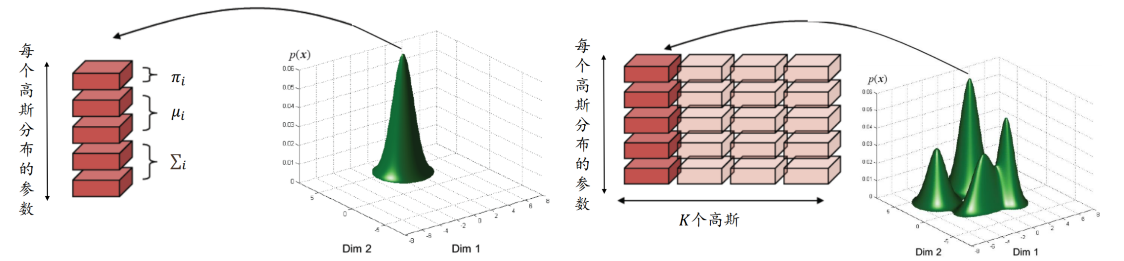
混合高斯分布

K个混合成分

第i个分布为高斯分布$N({\mu }_i,{\Sigma }_i)$

每个数据由以下生成过程产生：

P ( x j ) = ∑ i = 1 K P ( Y = i ) P ( x j ∣ Y = i ) P ( X = x j ∣ Y = i ) = 1 ( 2 π ) p / 2 1 ∣ Σ i ∣ 1 / 2 e x p { ? 1 2 ( x j ? μ i ) T Σ i ? 1 ( x j ? μ i ) } P(\pmb x_j)=\sum_{i=1}^KP(Y=i)P(\pmb x_j|Y=i)\\ P(X=\pmb x_j|Y=i)=\frac{1}{(2\pi)^{p/2}}\frac{1}{|\pmb\Sigma_i|^{1/2}}exp\{-\frac{1}{2}(\pmb x_j-\pmb\mu_i)^T\pmb\Sigma_i^{-1}(\pmb x_j-\pmb\mu_i)\} P(xxxj?)=i=1∑K?P(Y=i)P(xxxj?∣Y=i)P(X=xxxj?∣Y=i)=(2π)p/21?∣ΣΣΣi?∣1/21?exp{?21?(xxxj??μ?μ??μi?)TΣΣΣi?1?(xxxj??μ?μ??μi?)}

GMM聚类步骤

1?? 拟合高斯混合分布：估计K个参数 { μ i , Σ i } \{\mu_i,\Sigma_i\} {μi?,Σi?}——关键步骤
P ( x j ) = ∑ i = 1 K π i P ( x j ∣ y = i ) = ∑ i = 1 K π i P ( x j ∣ μ i , Σ i ) 其 中 P ( x j ∣ μ i , Σ i ) = 1 ( 2 π ) p / 2 1 ∣ Σ i ∣ 1 / 2 exp ? { ? 1 2 ( x j ? μ i ) T Σ i ? 1 ( x j ? μ i ) } 隐 变 量 π i = P ( y = i ) 。 P(x_j)=\sum_{i=1}^K\pi_iP(x_j|y=i)=\sum_{i=1}^K\pi_iP(x_j|\mu_i,\Sigma_i)\\ 其中P(x_j|\mu_i,\Sigma_i)=\frac{1}{(2\pi)^{p/2}}\frac{1}{|\Sigma_i|^{1/2}}\exp\{-\frac{1}{2}(x_j-\mu_i)^T\Sigma_i^{-1}( x_j-\mu_i)\}\\ 隐变量\pi_i=P(y=i)。 P(xj?)=i=1∑K?πi?P(xj?∣y=i)=i=1∑K?πi?P(xj?∣μi?,Σi?)其中P(xj?∣μi?,Σi?)=(2π)p/21?∣Σi?∣1/21?exp{?21?(xj??μi?)TΣi?1?(xj??μi?)}隐变量πi?=P(y=i)。

2?? 利用贝叶斯定理
$$P(y_j=i|x_j)=\frac{P(y_j=i)P(x_j|y_j=i)}{P(x_j)}=\frac{{\pi }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}{{\sum }_{i=1}^K{\pi }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}$$
3?? 对每个样本$x_j$，选择使后验概率最大的簇标记
$$i^{?}=\underset{i=1,2,?,K}{\mathrm{argmax}}P(y_j=i|x_j)$$

拟合高斯分布

GMM(Gaussian Mixture Model)

1?? 假设每一簇的数据服从一个高斯分布，对高斯分布的参数进行初始化

2?? 开始如下迭代：样本归簇、更新高斯分布的参数

3?? 参数不发生变化，停止迭代

最简单GMM：每个混合成分仅均值不同，具有相同的协方差矩阵${\sigma }^{2}I$

一般GMM：每个混合成分的均值和协方差矩阵均不同

极大似然估计（MLE），最大化如下对数似然函数的值

$$\ln (\prod _{j=1}^{n}P(x_j))=\ln (\prod _{j=1}^n\sum _{i=1}^K{\pi }_{i}P(x_j))$$
参数： θ = { π i , μ i , Σ i , i = 1 , 2 , . . . , K } \theta=\{\pi_i,\mu_i,\Sigma_i,i=1,2,...,K\} θ={πi?,μi?,Σi?,i=1,2,...,K}

对数里面有连加，不好求解——目标函数较为复杂，难以通过梯度上升处理

使用如下的EM算法

三、EM算法

聚类中数据不存在标签，因此需要添加隐标签

概述

处理隐变量分布的一种通用方法

可解释为在缺失（隐）变量数据下，最大似然估计的一种优化方法

迭代进行两个步骤

1?? E步（期望步）：基于当前参数${\theta }^t$，计算隐变量后验概率，进而计算对数似然期望值

2?? M步（最大化步）：更新参数，寻找能使E步产生的似然期望最大化的参数值

非魔法：只能找到局部最优

EM不直接对𝜃做极大似然估计，而是借助隐变量 y，生成 𝚯序列：
Θ = { θ ( 1 ) , θ ( 2 ) , . . . , θ ( t ) } \Theta=\{\theta^{(1)},\theta^{(2)},...,\theta^{(t)}\} Θ={θ(1),θ(2),...,θ(t)}
在EM的每一迭代步，执行
$${\theta }^{(t+1)}=\underset{\theta }{\mathrm{argmax}}\int P(y|X,{\theta }^{(t)})\ln P(X,y|\theta )dy$$

为了收敛，需要满足：

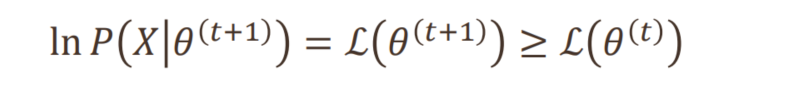
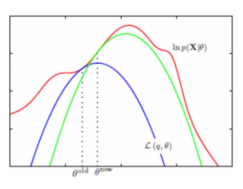
通俗地讲

为了求红色的目标函数的最优值

E步：先初始化参数${\theta }_1$，构造一个蓝色的函数，其方便求最优值

M步：求蓝色函数的最优值的参数${\theta }_2$

重复迭代：绿色……

EM推导

基于MLE估计最佳参数 ${\theta }_{MLE}$，有

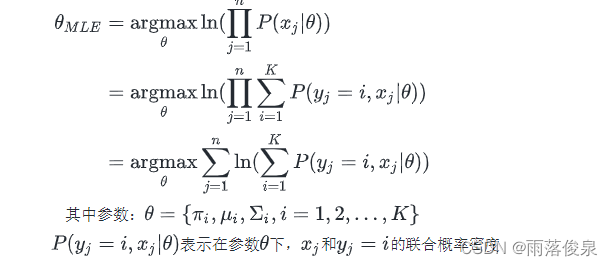
1?? E步：期望步——基于当前参数${\theta }^t$，计算隐变量后验概率，进而计算对数似然期望值

E步主要是计算对数联合概率$\ln P(x,y|\theta )$在后验概率$P(y|x,{\theta }^t)$ 分布下的期望，

EM的一次迭代为：

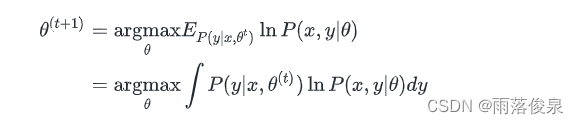
给定一组参数${\theta }^t$，计算隐变量后验概率(第j个样本在第i个簇的概率值)$P(y_j=i|x_j,{\theta }^t)$，由贝叶斯定理
$$P(y_j=i|x_j,{\theta }^t)=\frac{P(y_j=i)P(x_j|y_j=i)}{P(x_j)}=\frac{{\pi }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}{{\sum }_{i=1}^K{\pi }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}$$
通过Jensen不等式的性质构造出原目标函数的下界
$$\begin{gathered} \sum _{j=1}^n\sum _{i=1}^{K}P(y_j=i|x_j,{\theta }^t)\ln P(y_j=i,x_j|\theta )=\sum _{j=1}^n\sum _{i=1}^K{p}_{ji}\ln P(y_j=i,x_j|\theta ) \\ 其中p_{ji}=P(y_j=i|x_j,{\theta }^t) \end{gathered}$$
连加号移到了外面，同时加了个系数$p_{ji}$

$p_{ji}$由当前${\theta }^t$求出，求解上述目标函数可得新的${\theta }^{t+1}$,求解的过程由M步完成

2?? M步：最大化步——更新参数，寻找能使E步产生的似然期望最大化的参数值

对目标函数关于${\mu }_i$求偏导，则有

类似地，可以求得

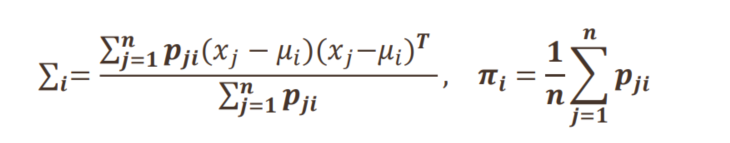
其中：
$$p_{ji}=P(y_j=i|x_j,{\theta }^t)=\frac{P(y_j=i)P(x_j|y_j=i)}{P(x_j)}=\frac{{\pi }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}{{\sum }_{i=1}^K{\pi }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}$$

算法再述

对于原来的目标函数

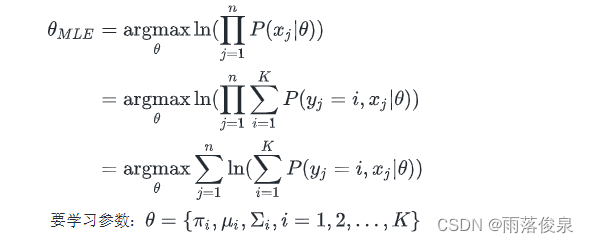
E步

给定一组参数${\theta }^t$，计算隐变量后验概率(第j个样本在第i个簇的概率值)$P(y_j=i|x_j,{\theta }^t)$，
$$P(y_j=i|x_j,{\theta }^t)=\frac{P(y_j=i)P(x_j|y_j=i)}{P(x_j)}=\frac{{\pi }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}{{\sum }_{i=1}^K{\pi }_{i}P(x_j|{\mu }_i,{\Sigma }_i)}$$
并构造新的目标函数：
∑ j = 1 n ∑ i = 1 K P ( y j = i ∣ x j , θ t ) ln ? P ( y j = i , x j ∣ θ ) = ∑ j = 1 n ∑ i = 1 K p j i ln ? P ( y j = i , x j ∣ θ ) 其 中 p j i = P ( y j = i ∣ x j , θ t ) 其 中 P ( y j = i , x j ∣ θ ) = P ( y j = i ) P ( x j ∣ y j = i , θ ) = π i P ( x j ∣ y j = i , θ ) P ( x j ∣ y j = i , θ ) = 1 ( 2 π ) p / 2 1 ∣ Σ i ∣ 1 / 2 exp ? { ? 1 2 ( x j ? μ i ) T Σ i ? 1 ( x j ? μ i ) } \sum_{j=1}^n\sum_{i=1}^KP(y_j=i|x_j,\theta^t)\ln P(y_j=i,x_j|\theta)=\sum_{j=1}^n\sum_{i=1}^Kp_{ji}\ln P(y_j=i,x_j|\theta)\\ 其中p_{ji}=P(y_j=i|x_j,\theta^t)\\ 其中P(y_j=i,x_j|\theta)=P(y_j=i)P(x_j|y_j=i,\theta)=\pmb \pi_iP(x_j|y_j=i,\theta)\\P(x_j|y_j=i,\theta)=\frac{1}{(2\pi)^{p/2}}\frac{1}{|\Sigma_i|^{1/2}}\exp\{-\frac{1}{2}(x_j-\mu_i)^T\Sigma_i^{-1}( x_j-\mu_i)\}\\ j=1∑n?i=1∑K?P(yj?=i∣xj?,θt)lnP(yj?=i,xj?∣θ)=j=1∑n?i=1∑K?pji?lnP(yj?=i,xj?∣θ)其中pji?=P(yj?=i∣xj?,θt)其中P(yj?=i,xj?∣θ)=P(yj?=i)P(xj?∣yj?=i,θ)=πππi?P(xj?∣yj?=i,θ)P(xj?∣yj?=i,θ)=(2π)p/21?∣Σi?∣1/21?exp{?21?(xj??μi?)TΣi?1?(xj??μi?)}

M步

对目标函数关于${\mu }_i,{\Sigma }_i,{\pi }_i$求偏导

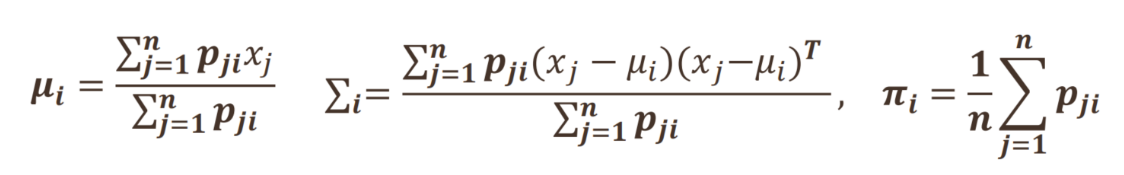
从而更新了参数

直观分析

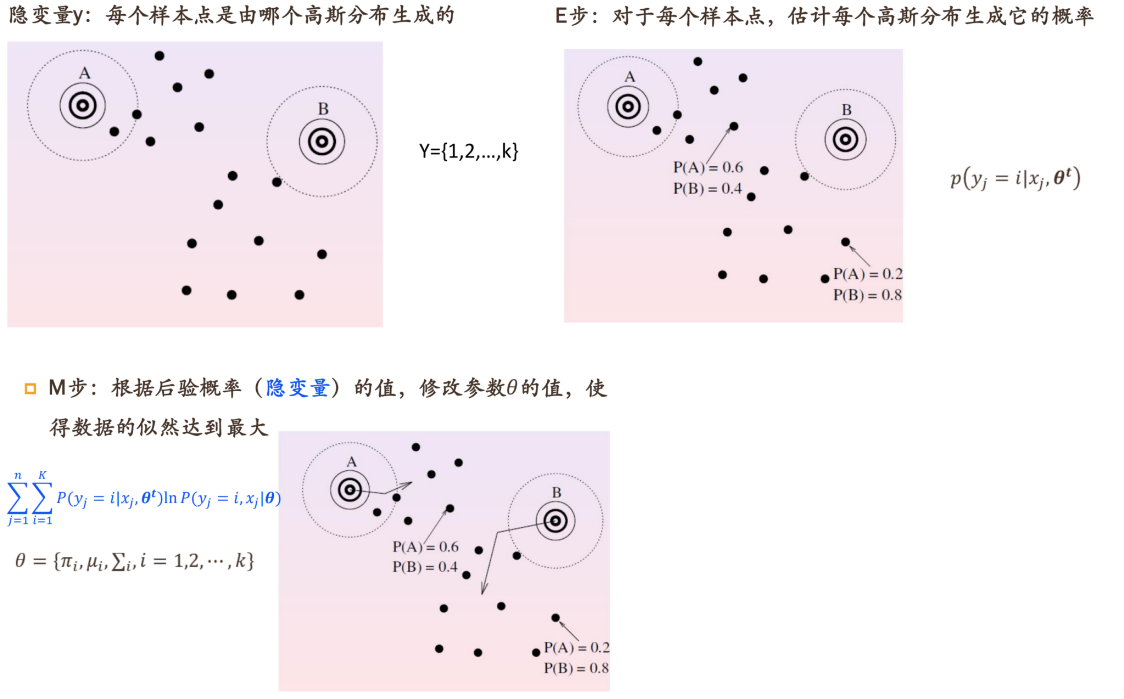
举例说明

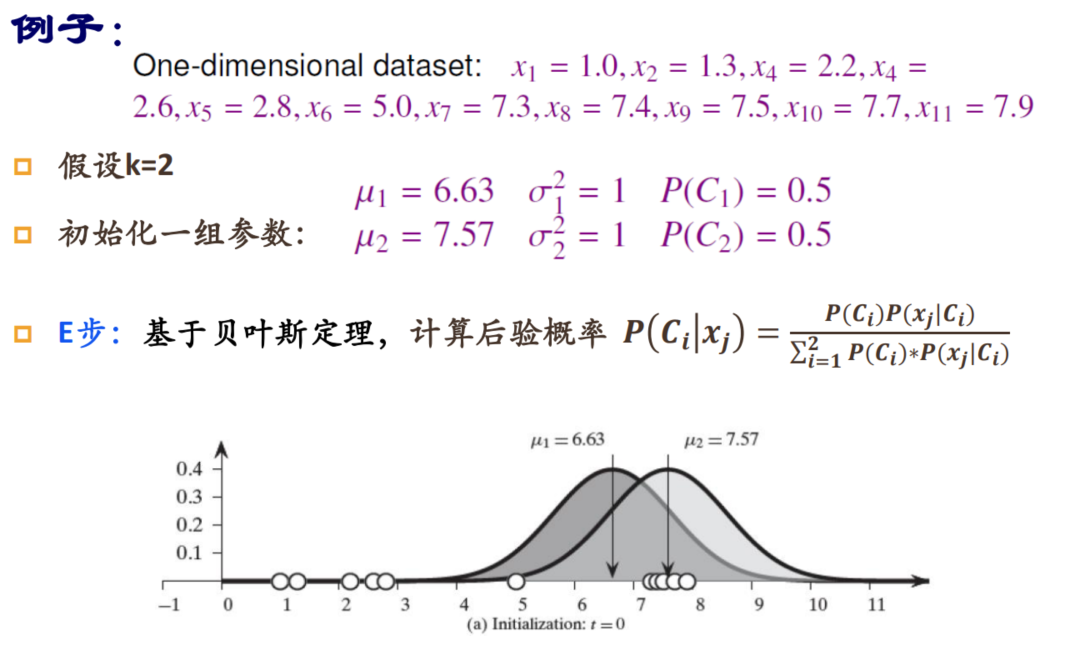
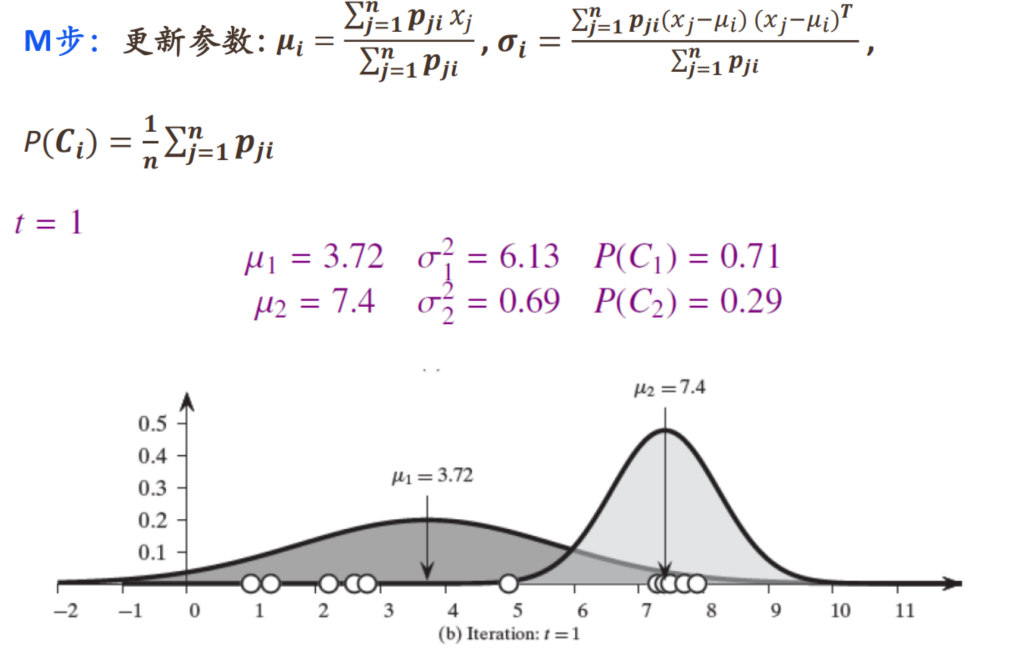
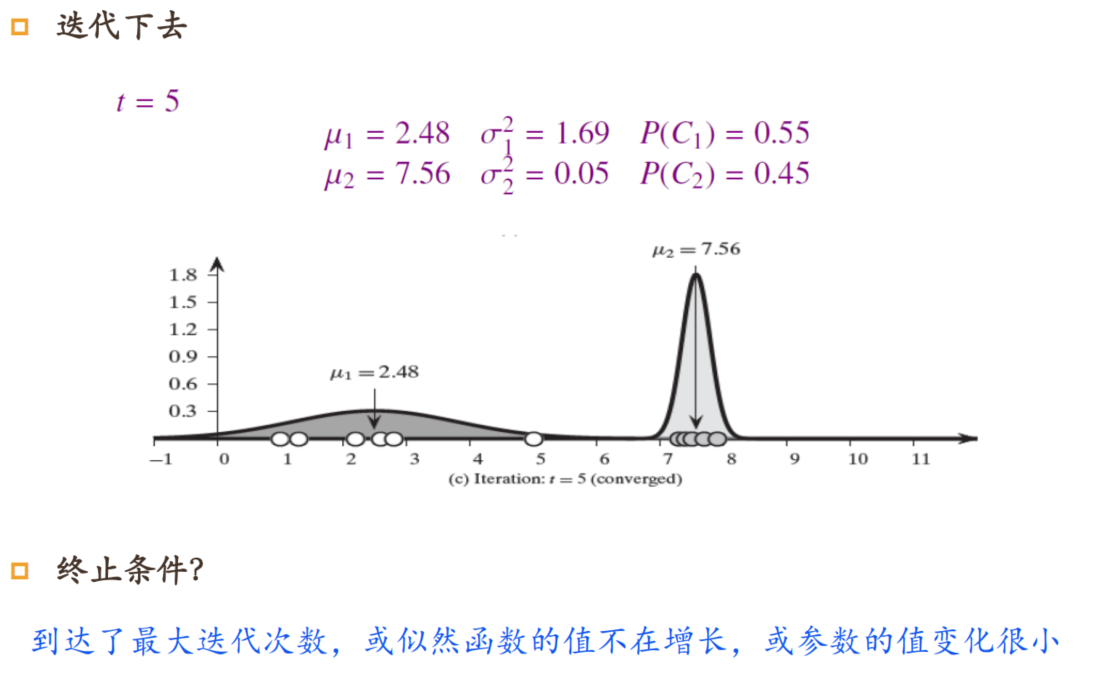
代码实现

import matplotlib.pyplot as plt
import numpy as np
import math

# 高斯分布函数
def gaussian(x, u, sigma_2):
    y = 1/((2*math.pi)**(1/2)*(np.sqrt(sigma_2))) * \
        np.exp(-0.5 * (x-u) * (x-u) / sigma_2)
    return y


# 计算后验概率
def cal_posteriori(i, x_j, pi, u, sigma, k):
    s = sum([pi[l]*gaussian(x_j, u[l], sigma[l]) for l in range(k)])
    temp = pi[i]*gaussian(x_j, u[i], sigma[i])
    return temp/s

# EM算法
def EM(x, k, u, sigma, pi, epoch):
    n = len(x)
    gamma = np.zeros((n, k))
    while epoch > 0:
        epoch -= 1
        # E步：计算后验概率
        gamma = \
            [
                [
                    cal_posteriori(i, x[j], pi, u, sigma, k)
                    for i in range(k)
                ]for j in range(n)
            ]
        # M步，更新参数
        u =\
            [
                sum([gamma[j][i]*x[j] for j in range(n)]) /
                sum([gamma[j][i] for j in range(n)])
                for i in range(k)
            ]

        for i in range(k):
            A = sum([gamma[j][i]*(x[j]-u[i])*(x[j]-u[i]) for j in range(n)])
            B = sum([gamma[j][i] for j in range(n)])
            sigma[i] = A/B
        pi = [sum([gamma[j][i] for j in range(n)])/n for i in range(k)]
    # 存储分类后的x
    C = [[] for j in range(k)]

    for j in range(n):
        lmbda = 0
        for i in range(k):
            if gamma[j][i] > gamma[j][lmbda]:
                lmbda = i
        # 分类
        C[lmbda].append(x[j])

    for i in range(k):
        print('C{}={}'.format(i+1, C[i]))

    return (C, u, sigma, pi)


x = [1.0, 1.3, 2.2, 2.6, 2.8, 5.0, 7.3, 7.4, 7.5, 7.7, 7.9]
k = 2  # 两类
u = [6, 7.5]  # 初始均值
sigma = [1, 1]  # 初始sigma
pi = [0.5, 0.5]
epoch = 20

C, u, sigma, pi = EM(x, k, u, sigma, pi, epoch)

# 绘制图像
x_2 = np.linspace(-5, 11, 5000)
plt.figure()
for i in range(k):
    u_i = u[i]
    sigma_i = sigma[i]
    y = gaussian(x_2, u_i, sigma_i)
    plt.plot(x_2, y)
plt.legend(['u1={:.2f},sigma1={:.2f},P(C1)={:.2f}'.format(
            u[0],  sigma[0],  pi[0]), 'u2={:.2f},sigma2={:.2f},P(C2)={:.2f}'.format(
            u[1],  sigma[1],  pi[1])])
for i in range(len(C[0])):
    plt.scatter(C[0][i], 0, s=16, c='blue', alpha=1)
for i in range(len(C[1])):
    plt.scatter(C[1][i], 0, s=16, c='red', alpha=1)
plt.show()

运行结果

C1=[1.0, 1.3, 2.2, 2.6, 2.8, 5.0]
C2=[7.3, 7.4, 7.5, 7.7, 7.9]

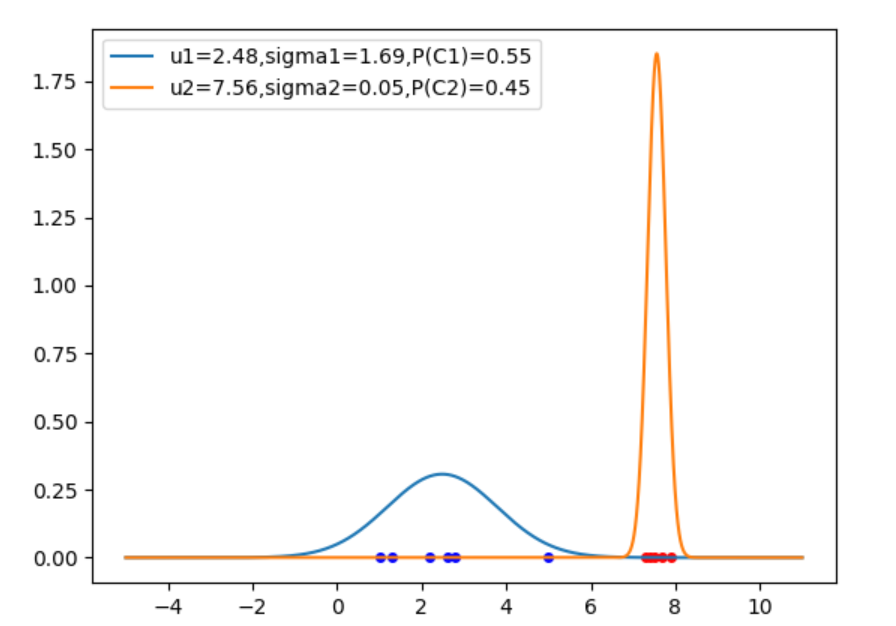
四、GMM和K-means比较

K-means是EM算法的特例：每个高斯的协方差相同且已知，只学习参数${\mu }_k$ (1D)

假设在第t步已学到了K个聚类中心 { μ 1 ( t ) , μ 2 ( t ) , . . . , μ k ( t ) } \{\mu_1^{(t)},\mu_2^{(t)},...,\mu_k^{(t)}\} {μ1(t)?,μ2(t)?,...,μk(t)?} ,第t +1步迭代

E步：计算$x_j$属于第k类的概率

构造目标函数：
$$\sum _{j=1}^n\sum _{i=1}^{K}P(y_j=i|x_j,{\theta }^t)\ln P(y_j=i,x_j|\theta )$$

M步：

比较

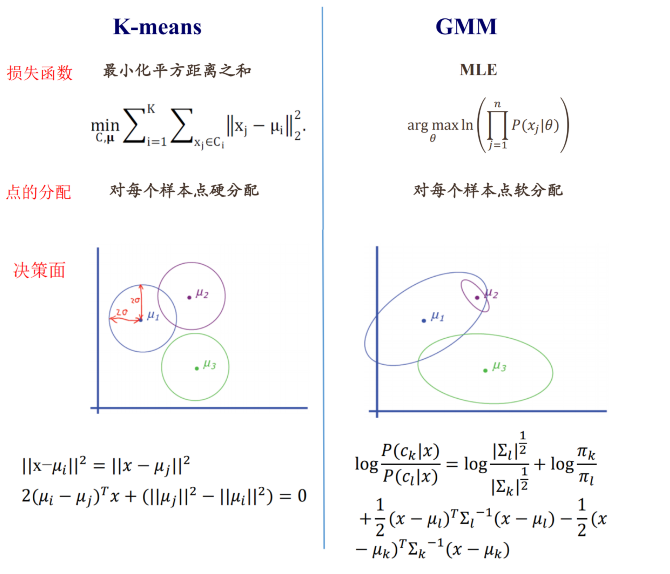
GMM缺点

假设数据服从混合高斯分布

EM算法中的参数过多，对初始参数值比较敏感。可以使 用k-means对均值和先验概率赋初值

与k-means一样，选择聚类数目K至关重要

GMM 缺点：计算复杂度比 k-means 高

参考资料

[1]庞善民.西安交通大学机器学习导论2022春PPT

[2]周志华.机器学习.北京:清华大学出版社,2016

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖