一. 平移
① 平移的原理
平移就是将图像中的所有的点按照平移量水平或者垂直的移动.
假设要水平右侧移动100个像素,向下移动50个像素,则原图像和目标图像的对应关系为:
dst(x,y) = src(x + 100,y + 50)就是一个坐标变换,将原来的位置(0,0)的像素值,赋值给位置是(100,50)的位置,然后后面的像素都按照这种规则替换
可以转换为
dst(x,y) = src(x * 1 + y * 0 + 100,x * 0 + y * 1 +50)
表示为矩阵就是:
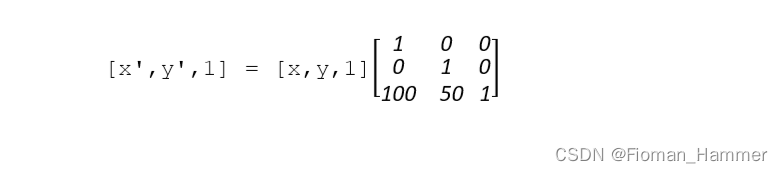
设tx和ty分别为水平方向和垂直方向偏移量,水平向右为正,垂直向下为正,所以平移的转换矩阵为:
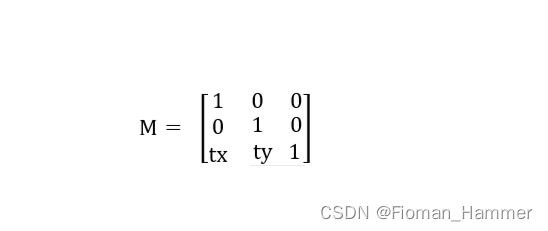
② 平移实现
平移也是一种仿射变换,所有的仿射变换都使用同一个函数
wrapAffine函数原型:
void warpAffine( InputArray src, OutputArray dst,
InputArray M, Size dsize,
int flags = INTER_LINEAR,
int borderMode = BORDER_CONSTANT,
const Scalar& borderValue = Scalar());
参数说明:
src:源图像dst:输出图像M:变换矩阵flags:变换的时候使用的线性插值算法boardMode:边界像素填充模式boardValue:边界填充像素值,当boardMode为const的时候,才会用到这个值
关于线性插值的几种方式:
其中flags的可以取的值如下:
enum InterpolationFlags
{
INTER_NEAREST = 0, // 最近邻插值法
INTER_LINEAR = 1, // 双线性插值法
INTER_CUBIC = 2,
INTER_AREA = 3,
INTER_LANCZOS4 = 4,
INTER_LINEAR_EXACT = 5,
INTER_NEAREST_EXACT = 6,
INTER_MAX = 7,
WARP_FILL_OUTLIERS = 8,
WARP_INVERSE_MAP = 16
};
最近邻插值算法的原理:
最近邻插值,是指将目标图像中的点,对应到原图像中后,根据距离,找到最相邻的整数点的像素值,作为该点的额像素值输出
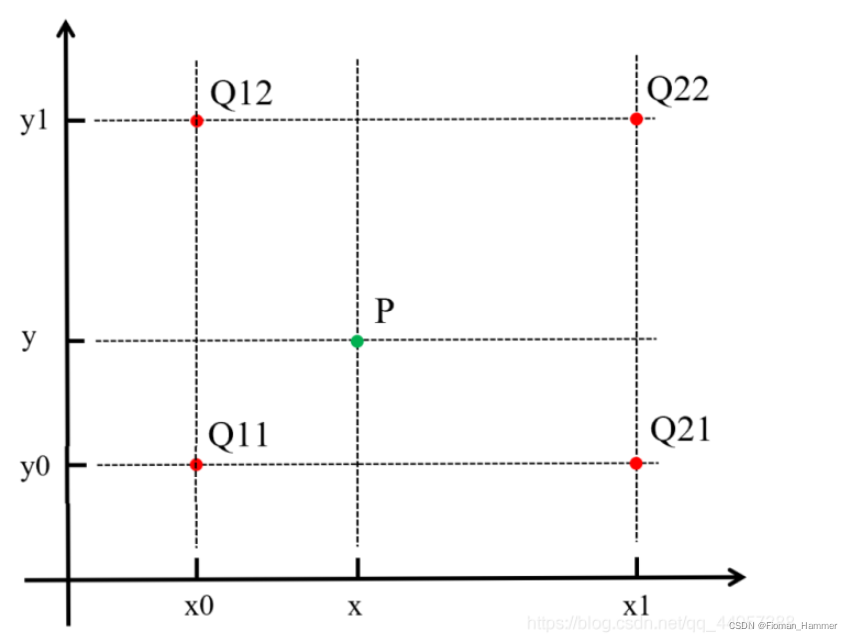
如上图所示,目标图像中某点投影到原图像中的位置为点P,点P是小数,其周围四个整数点位Q11,Q12,Q22,Q21,因为Q11离P最近,所以可以知道f§ = f(Q11)
举个例子,创建一个2*2的图像矩阵,里面存放(1,2,3,4)
如果偏移0.7个像素,向右和向下同时偏移.则目标图像的点位分别为
dst(0,0) = src(-0.7,-0.7) = src(-1,-1) = 0
dst(0,1) = src(-0.7,0.3) = src(-1,0) = 0
dst(1,0) = src(0.3,-0.7) = src(0,-1) = 0
dst(1,1) = src(0.3,0.3) = src(0,0) = 1
下面写代码验证一下:
#include "MyOpencv.h"
int main(void)
{
Mat imageSrc = Mat::zeros(Size(2, 2), CV_8UC1);
int rows = imageSrc.rows;
int cols = imageSrc.cols;
for (int row = 0; row < rows; row++)
{
uchar *pCurrent = imageSrc.ptr<uchar>(row);
for (int col = 0; col < cols; col++)
{
*pCurrent++ = row * 2 + col + 1;
}
}
for (int row = 0; row < rows; row++)
{
uchar *pCurrent = imageSrc.ptr<uchar>(row);
for (int col = 0; col < cols; col++)
{
cout << int( * pCurrent++ )<< " ";
}
cout << endl;
}
Mat dst;
// 注意Size是宽和高(对应的是列和行) 2行3列
Mat M = Mat::zeros(Size(3, 2), CV_32FC1);
Size newSize = imageSrc.size();
M.at<float>(0, 0) = 1;
M.at<float>(0, 2) = 0.7f;
M.at<float>(1, 1) = 1;
M.at<float>(1, 2) = 0.7f;
// 现在是将图像向右向下平移0.7个像素
cv::warpAffine(imageSrc, dst, M, newSize, INTER_NEAREST);
cout << "平移之后,最近邻插值法的计算结果: " << endl;
for (int row = 0; row < rows; row++)
{
uchar *pCurrent = dst.ptr<uchar>(row);
for (int col = 0; col < cols; col++)
{
cout << int(*pCurrent++) << " ";
}
cout << endl;
}
return 0;
}
结果:
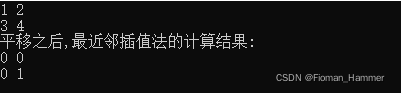
可以更改下平移的方向,比如把平移改成-0.7,则得到的结果推导一下:
dst(0,0) = src(0.7,0.7) = src(1,1) = 4
dst(0,1) = src(0.7,1.7) = src(1,2) = 0
dst(1,0) = src(1.7,0.7) = src(2,1) = 0
dst(1,1) = src(1.7,1.7) = src(2,2) = 0
结果:

最近邻插值法的优缺点:
最近邻插值法速度比较快,但是放大后的图像有严重的马赛克,会出现明显的块状效应,缩小后的图像有严重的失真.
双线性插值法原理:
先看看线性插值
- 使用连接两个已知量的直线来确定这两个已知量之间的一个未知量的值.
- 公式
f(x) = k * x + b
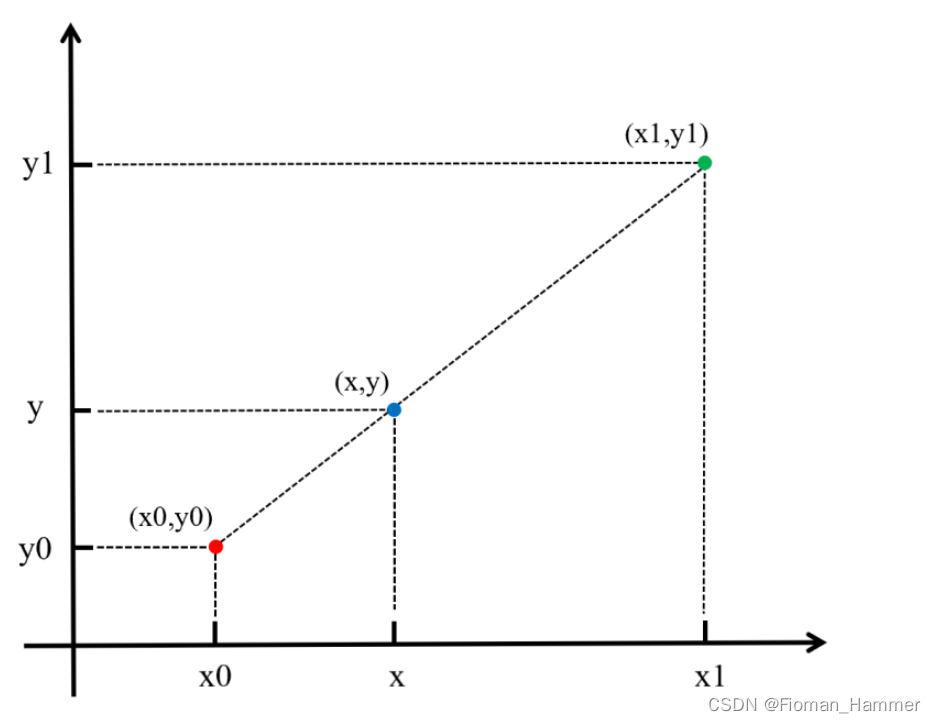
线性插值多项式:
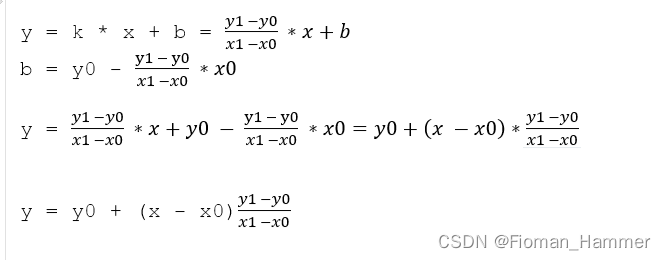
即使x不在x0和x1之间,这个公式也是成立的.这种情况下,叫做线性外插.
线性插值的误差: 线性插值其实就是拉格朗日插值有两个结点的情况.
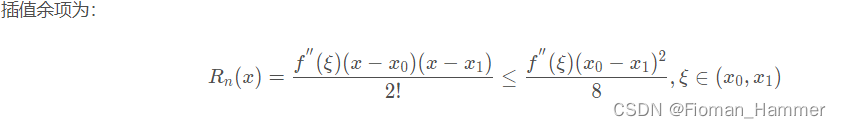
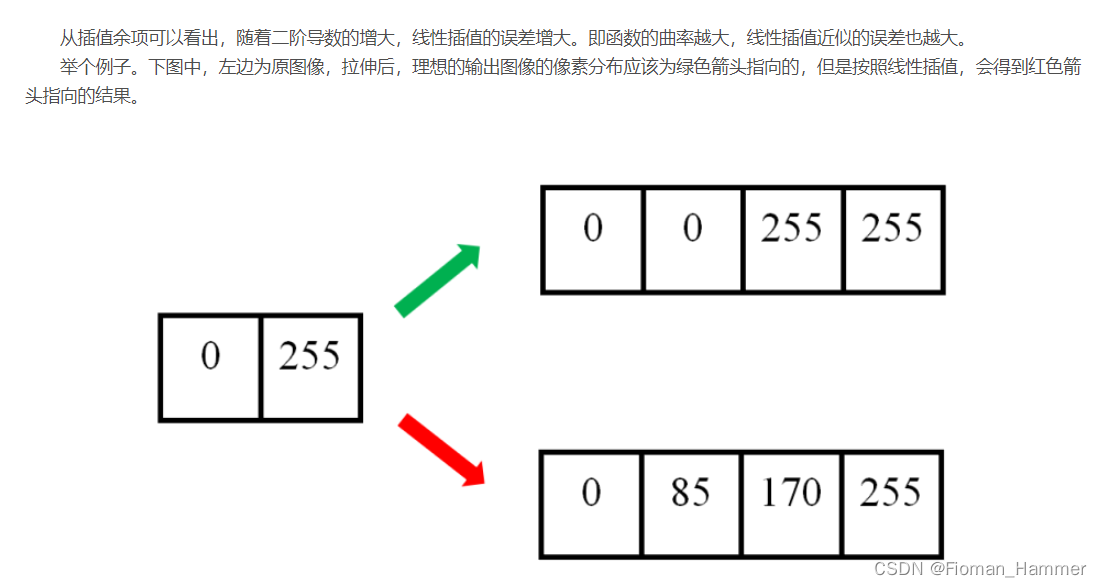
双线性插值:
f(x,y) = ax + by + cxy + d
双线性插值是线性插值在二维时的推广,在两个方向上共做了三次线性插值.定义了一个双曲抛物面与四个已知点拟合.具体操作为在X方向上进行两次线性插值计算,然后再Y方向上进行一次插值计算.
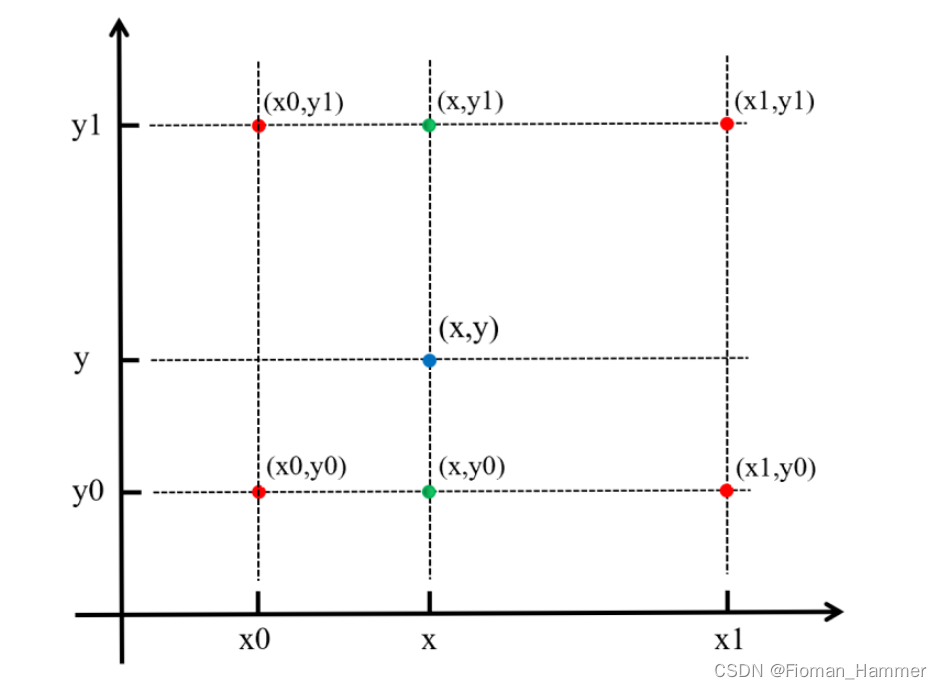
x方向的插值算法,其实是根据距离的权重去计算的,距离的越近,权重越大,距离的越远,权重越小
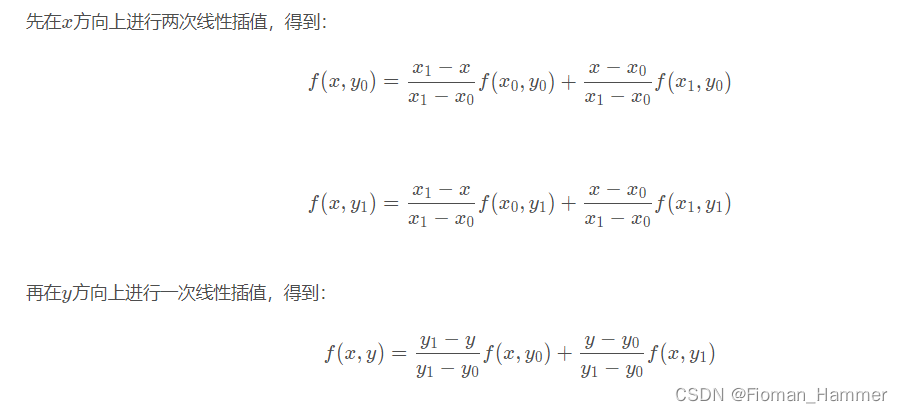
其实就是按照(x,y)到四个已知点的距离,然后根据权重去乘以对应的像素值,显示x方向上,再然后是y方向上.
举例:
现在我们算一算Size(3,3) = [10,20,30,40,50,60] 像素,向右下平移0.7个像素之后的结果:
dst(0,0) = src(-0.7,-0.7)
它的四个点分别为(-1,-1),(0,-1),(-1,0),(0,0)
先做X方向上的线性插值
f(x,y0) = f(-1,0) * 0.7 + f(0,0) * 0.3 = 10 * 0.3 = 3
f(x,y1) = f(-1,0) * 0.7 + f(0,-1) * 0.3 = 0
f(x,y) = 3 * 0.3 + 0 * 0.7 = 0.9 = 1(这里四舍五入)
dst(0,1) = src(-0.7,0.3)
它的四个点分别为(-1,0),(0,0),(-1,1),(0,1)
f(x,y0) = f(-1,0)0.7 + f(0,0) * 0.3 = 3
f(x,y1) = f(-1,1) * 0.7 + f(0,1) * 0.3 = 20 0.3 = 6
f(x,y) = 3 * 0.7 + 6 * 0.3 = = 3.9 = 4
验证:
#include "MyOpencv.h"
int main(void)
{
Mat imageSrc = Mat::zeros(Size(3, 3), CV_8UC1);
int rows = imageSrc.rows;
int cols = imageSrc.cols;
for (int row = 0; row < rows; row++)
{
uchar *pCurrent = imageSrc.ptr<uchar>(row);
for (int col = 0; col < cols; col++)
{
*pCurrent++ = (row * 2 + col + 1) * 10;
}
}
for (int row = 0; row < rows; row++)
{
uchar *pCurrent = imageSrc.ptr<uchar>(row);
for (int col = 0; col < cols; col++)
{
cout << int( * pCurrent++ )<< " ";
}
cout << endl;
}
Mat dst;
// 注意Size是宽和高(对应的是列和行) 2行3列
Mat M = Mat::zeros(Size(3, 2), CV_32FC1);
Size newSize = imageSrc.size();
M.at<float>(0, 0) = 1;
M.at<float>(0, 2) = 0.7f;
M.at<float>(1, 1) = 1;
M.at<float>(1, 2) = 0.7f;
// 现在是将图像向右向下平移0.7个像素
cv::warpAffine(imageSrc, dst, M, newSize, INTER_LINEAR);
cout << "平移之后,最近邻插值法的计算结果: " << endl;
for (int row = 0; row < rows; row++)
{
uchar *pCurrent = dst.ptr<uchar>(row);
for (int col = 0; col < cols; col++)
{
cout << int(*pCurrent++) << " ";
}
cout << endl;
}
return 0;
}
结果:
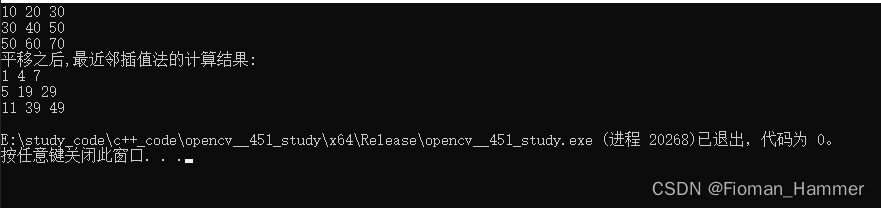
可以看到结果是正确的.
双三次插值算法INTER_CUBIC
双三次插值算法是基于周围的4*4=16个像素点,通过计算16个像素点的权重,累计得到增加点的像素值.
具体的过程就不讲了.
区域插值 INTER_AREA
区域插值共分为三种情况,图像放大的时候类似于双线性插值,图像缩小(x,y轴同时缩小)又分为两种情况,此情况下可以避免波纹出现.因此对图像进行缩小的时候,为了避免出现波纹现象,推荐采用区域插值算法.
二. 旋转
① 旋转原理
设点(x0,y0)逆时针旋转θ之后对应的点位(x,y),之前的这个点的角度为α,则旋转之后的(x,y)的坐标
x = r * cos(α +θ) = r * cos α * cosθ - r * cos α * cosθ = x0 * cosθ - y0 * sinθ
y = r * sin(α + θ) = r * sinα * cosθ + r * cosα * sinθ = x0 * sin θ + y0 * cosθ
所以旋转矩阵为
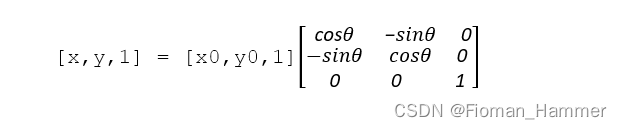
Opencv提供了具有可调旋转中心的缩放旋转,因此可以在任何的位置旋转和缩放.
旋转也是仿射变换的一种,所以操作的函数还是warpAffine,但是它的变换矩阵,不像平移那么简单,所以Opencv提供了一个专门求旋转变换矩阵的函数
② 旋转实现
函数原型:
Mat getRotationMatrix2D(Point2f center, double angle, double scale);
参数解释:
center:图像的旋转中心angle:旋转角度.正数表示逆时针旋转,负数表示顺时针旋转scale:缩放系数
#include "MyOpencv.h"
int main(void)
{
Mat imageSrc = Mat::zeros(Size(800, 800), CV_8UC3);
int rows = imageSrc.rows;
int cols = imageSrc.cols;
// 画一个矩形300 * 300的
cv::rectangle(imageSrc, Rect(200, 200, 300, 300), Scalar(0, 0, 255), -1, LINE_4);
// 然后逆时针旋转45度,并且缩小一倍,按照图像中心旋转
Mat M = getRotationMatrix2D(Point(cols / 2, rows / 2), 45, 1);
Mat dst;
cv::warpAffine(imageSrc, dst, M, Size(800, 800), INTER_AREA);
imshow("Original", imageSrc);
imshow("Rotated45ImageCenter", dst);
// 按照左上角进行旋转
M = getRotationMatrix2D(Point(200, 200), 45, 1);
cv::warpAffine(imageSrc, dst, M, Size(800, 800), INTER_AREA);
imshow("Roateed45LeftTop", dst);
waitKey(0);
return 0;
}
三.翻转(镜像)
① 翻转原理
- 翻转也称为镜像变换,反转后图像原图像是对称的
- 反转分为绕X轴反转,绕Y轴反转,绕X轴和Y轴同时反转三种情况
几种翻转对应的情况:
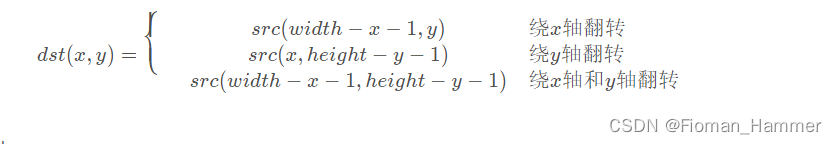
② 反转实现
函数原型:
void flip(InputArray src, OutputArray dst, int flipCode);
参数说明:
src:原图像dst:目标图像flipCode:反转方式: 0表示沿x轴反转, >0例如1表示沿y轴反转, <0比如-1表示沿x轴y轴反转
#include "MyOpencv.h"
int main(void)
{
Mat imageSrc = Mat::zeros(Size(800, 800), CV_8UC3);
Mat roiMat = imageSrc(Range(0, 399), Range(0, 399));
roiMat = Scalar(0, 0, 255); // 左上角红色
roiMat = imageSrc(Range(0, 399), Range(400, 799));
roiMat = Scalar(255, 0,0); // 右上角蓝色
roiMat = imageSrc(Range(400, 799), Range().all());
roiMat = Scalar(125, 125, 125); // 下面全部是灰色
imshow("Original", imageSrc);
// 上下镜像,代表绕着x轴进行翻转,y坐标进行镜像替换
Mat dst;
flip(imageSrc, dst, 0);
imshow("Flip_X", dst);
// 左右镜像,代表绕着y轴进行翻转,x坐标进行镜像替换
flip(imageSrc, dst, 1);
imshow("Flip_Y", dst);
// 上下左右同时镜像, 沿着x和y一起翻转
flip(imageSrc, dst, -1);
imshow("Flip_XY", dst);
waitKey(0);
return 0;
}
四. 缩放
① 几何变换的基本概念
图像的集合变换改变了像素的空间位置,建立一种原图像像素与变换后图像像素之间的映射关系,通过这种映射不安息能够实现下面两种计算:
1. 原图像任意像素计算该像素在变换后图像的坐标位置
2. 变换后图像的任意像素在原图像的坐标位置
对于第一种计算,只要给出原图像上的任意像素坐标,就能通过对应的映射关系获取该像素在变换后图像的坐标位置.将这种输入图像坐标映射到输出的拖成称为向前映射,反过来,知道任意变换图像上的像素坐标,计算其在原图像的像素坐标,将输出图像映射到输入的过程称为向后映射.在使用向前映射处几何变换时却有一些不足,通常会有两个问题: 映射不完全,映射重叠
1. 映射不完全:
输入图像的像素总数小于输出图像,这样输出图像中的一些像素找不到再原图像中的映射.
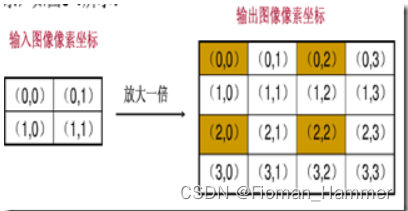
上图只有(0,0),(0,2),(2,0),(2,2)四个坐标根据映射关系在原图中找到对应的像素,其余的12个坐标没有有效值.
2.映射重叠
根据映射关系,输入图像的多个像素映射到输出图像的同一个像素上.

上图左上角的四个像素(0,0),(0,1),(1,0),(1,1)都会映射到输出图像(0,0)上,那么(0,0)究竟是取哪个像素值呢?
要解决上述两个问题,可以使用向后映射,使用输出图像的坐标反过来推算该坐标对应于原图像中的坐标位置.这样,输出图像的每个像素都可以通过映射关系在原图像找到唯一对应的像素,而不会出现映射不完全和映射重叠.所以,一般使用向后映射来处理图像的几何变换.向前映射之所以会出现问题,一般是因为图像的像素总数发生了变化,对于图像的像素总数不发生变化的情况,向前映射也是有效的
② 图像缩放原理
图像的缩放指的是图像的尺寸变大或者变小的过程,也就是增加或者减小原图像数据的像素的个数.
简单的来说,就是通过增加或者删除像素点来改变图像的尺寸.当图像缩小的时候,图像会变得更加清晰,当图像放大的时候,图像质量会有有所下降,因此需要进行插值处理.
设水平缩放系数为sx,垂直缩放系数为sy,(x0,y0)为缩放前坐标,(x,y)为缩放后坐标,其缩放的坐标映射关系:

矩阵表示形式:
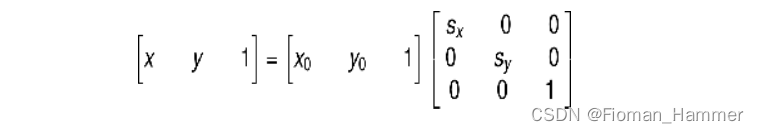
这是向前映射,在缩放的过程改变了图像的大小,使用向前映射会出现映射重叠和映射不完全的问题,所以这里更关系的是向后映射,也就是输出图像通过向后映射关系找到其在原图像中的对应的像素.
向后映射关系:
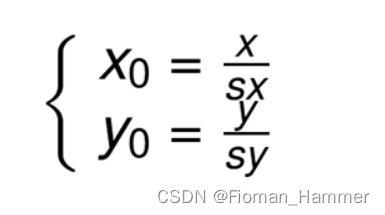
③ 图像缩放实现
函数原型:
void resize( InputArray src, OutputArray dst,
Size dsize, double fx = 0, double fy = 0,
int interpolation = INTER_LINEAR );
参数解释:
src:输入图像dst:输出图像dsize:输出图像的尺寸,如果是0,会按照Size(round(fx * src.cols),round(fy*src.rows))fx:x轴方向的缩放比例,当是0的时候,会按照dsize.width/src.cols进行计算fy:y轴方向的缩放比例,但是0的时候,胡先找dsize.height/src.rows进行计算interpolation:插值方式,一般缩小使用INTER_AREA放大使用INTER_LINEAR
#include "MyOpencv.h"
int main(void)
{
Mat imageSrc = Mat::zeros(Size(800, 800), CV_8UC3);
cv::rectangle(imageSrc, Rect(100, 100, 300, 300), Scalar(0, 255, 0), -1, LINE_4);
// 按照固定的尺寸进行缩放
Size newSize = Size(400, 600);
Mat dst;
resize(imageSrc, dst, newSize,0,0,INTER_AREA);
imshow("Original", imageSrc);
imshow("Resize(400,400)", dst);
// 按照x轴和y轴进行缩放
resize(imageSrc, dst, Size(), 0.2, 0.5, INTER_AREA);
imshow("Resize(0.5,0.5)", dst);
// 如果指定了尺寸,后面再指定fx和fy也灭有用了
resize(imageSrc, dst, Size(200, 200), 1.5, 1.5, INTER_AREA);
imshow("Resize(200,200)", dst);
waitKey(0);
return 0;
}
