1.软件版本
MATLAB2019a
2.本算法理论知识
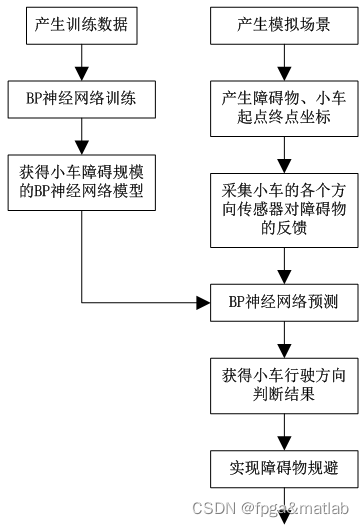
BP(Back Propagation)神经网络,其本质是一种基于误差反馈传播的神经网络算法。从结构上讲,BP神经网络是由一个信息的正向传播网络和一个误差的反向传播网络两个模块构成。BP神经网络的结构如下图所示:
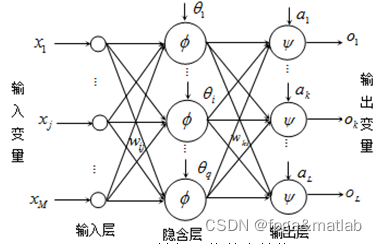
???? ????从图1的结构可知,BP神经网络主要由输入层,隐含层以及输出层三个部分构成。来自外界的信息通过输入层传输进入到隐含层进行处理,并由输出层输出处理结果。当BP神经网络的输出结果和其期望结果之间的误差较大的时候,则进入反向传播阶段,并进行进行审计网络权值的修正,直到输出结果和期望结果误差满足一定条件为止。
3.部分源码
clc;
clear;
close all;
warning off;
addpath 'func\'
%小车行驶步进
lambda = 0.1;
Ns = 32;
%传感器有效半径
Sense_radius = 2;
%定义一些变量,用于循环过程中的赋值
xs = zeros(2,Ns);
G1(:,1) = zeros(Ns,1);
G2(:,1) = zeros(Ns,1);
G3(:,1) = zeros(Ns,1);
Jd(:,1) = zeros(Ns,1);
for m=2:Ns
Jd(m,1)=Jd(m-1,1)+(pi/180)*(360/Ns);
end
%障碍物个数
N = 18;
%场景大小
Len = 25;
xmin = [0;0];
xmax = [Len;Len];
%障碍物和场景的间隔
SIZE = 6;
figure(1);
%产生障碍物
[xobstacle,yobstacle,R] = func_obstacles(N,SIZE,Len);
%起点和终点
X_start = 1;
Y_start = 1;
%起点和终点
X_end = 20;
Y_end = 20;
hold on
%画图
plot(X_start,Y_start,'rs');%画图
hold on
plot(X_end,Y_end,'rs');
Pend =[X_end;Y_end];
x(:,1) =[X_start;Y_start];
x(:,2) =[X_start;Y_start];
x(:,3) =[X_start;Y_start];
axis([0,Len,0,Len]);
axis square
text(X_start+1,Y_start+1,'START');
text(X_end+1,Y_end+1,'END');
hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%根据样本数据进行训练
%注意,这里缺少大量的测试样本,故暂用自己编写数据进行模拟
NN = 10;
for ii = 1:NN
tmps1 = (randperm(3)-2);
data1(ii) = tmps1(1);
end
A =[30*rand(1,10);30*rand(1,10);data1+30*rand(1,10);20*rand(1,10)]';
B =[data1]';
pstudy = A;
ptest = B/100;
trnData = pstudy;
chkData = ptest;
%创建BP神经网络
net = newff(trnData',chkData',20) ;
%设置训练参数
net.trainparam.show = 50 ;%显示
net.trainparam.epochs = 500 ;%迭代次数
net.trainparam.goal = 1e-20;%优化目标
net.trainParam.lr = 0.01 ;%学习参数
%开始训练神经网络
net = train(net,trnData',chkData') ;
figure(1);
%实时计算机器人三个传感器和障碍物的距离
TIME = 400;
Vs = [];
Tes = [];
Xs = zeros(1,TIME);
Ys = zeros(1,TIME);
x(:,4:TIME)= zeros(2,TIME-3);
%根据时间开始循环
for time = 1:TIME
time
%计算四个输入
if time <= 3
x(:,time)= min(x(:,time),xmax);
x(:,time)= max(x(:,time),xmin);
Xs(time) = X_start;
Ys(time) = Y_start;
Theta = atan((Y_end-Y_start)/(X_end-X_start));
else
x(:,time)= min(x(:,time),xmax);
x(:,time)= max(x(:,time),xmin);
%计算alpha,机器人运动方向与目标方向之间的夹角
%计算alpha,机器人运动方向与目标方向之间的夹角
if X_end-Xs(time-1) == 0
tmps1 = inf;
else
tmps1 =(Y_end-Ys(time-1))/(X_end-Xs(time-1));
end
if Xs(time-1)-Xs(time-2) == 0
tmps2 = inf;
else
tmps2 =(Ys(time-1)-Ys(time-2))/(Xs(time-1)-Xs(time-2));
end
%目标方向 %运动方向
alpha = atan(tmps1) - atan(tmps2);
%先计算障碍物和机器人的距离,然后将这些距离划分为四类,dr,d,dl和反方向的,如果没有,那么认为距离为inf
dr = [];
dl = [];
d = [];
vdr = [];
vdl = [];
vd = [];
for kk = 1:N
%计算距离,障碍物和小车当前位置的间距
dist(kk) = sqrt((xobstacle(kk)-Xs(time-1))^2 + (yobstacle(kk)-Ys(time-1))^2)-R(kk);
if xobstacle(kk)-Xs(time-1) == 0
vdist(kk) = 1;
else
vdist(kk) = sign((yobstacle(kk)-Ys(time-1))/(xobstacle(kk)-Xs(time-1)));
end
if dist(kk)>0
%计算各个距离和机器人运动方向的夹角
if xobstacle(kk)-Xs(time-1) == 0
tmps3 = inf;
else
tmps3 =(yobstacle(kk)-Ys(time-1))/(xobstacle(kk)-Xs(time-1));
end
Beta(kk) = (atan(tmps3))*180/pi;
%根据角度差,分析哪些是dr,d,dl和反方向
%说明这个障碍物在运动方向的右边
if Beta(kk) > 15 & Beta(kk) <= 75
dr = [dr,dist(kk)];
dl = dl;
d = d;
vdr = [vdr,vdist(kk)];
vdl = vdl;
vd = vd;
end
%说明这个障碍物在运动方向的左边边
if Beta(kk) < -15 & Beta(kk) >= -75
dr = dr;
dl = [dl,dist(kk)];
d = d;
vdr = vdr;
vdl = [vdl,vdist(kk)];
vd = vd;
end
%说明这个障碍物在运动方向的前边
if Beta(kk) <= 15 & Beta(kk) >= -15
dr = dr;
dl = dl;
d = [d,dist(kk)];
vdr = vdr;
vdl = vdl;
vd = [vd,vdist(kk)];
end
end
end
for m=1:Ns
xs(:,m) = [x(1,time-1) + Sense_radius*cos(Jd(m,1));
x(2,time-1) + Sense_radius*sin(Jd(m,1))];
G1(m,1) = func_obstacle(xs(:,m),xobstacle,yobstacle);
G2(m,1) = func_goal(xs(:,m),Pend);
G3(m,1) = G1(m,1) + G2(m,1);
end
[val,bestone]=min(G3);
%如果某个方向有多个障碍物,那么选择最近的那个
%如果某个方向的距离集合为空集合,那么说明这个方向的障碍物为无穷远,直接赋值一个较大值
dr_in = min(dr);
if isempty(dr) == 1
dr_in = 1e20;
end
d_in = min(d);
if isempty(d) == 1
d_in = 1e20;
end
dl_in = min(dl);
if isempty(dl) == 1
dl_in = 1e20;
end
%代入到BP神经网络的四个变量
%调用BP神经网络的模型
YOUT = func_nn_test(dr_in,d_in,dl_in,alpha,net);
%计算速度和方向
DELTA_Theta = YOUT/10;
V = YOUT;
%更新小车坐标
x(:,time) =[x(1,time-1)+lambda*cos(Jd(bestone,1));
x(2,time-1)+lambda*sin(Jd(bestone,1))];
Deltalambda = V;
Deltatheta = DELTA_Theta;
%更新小车坐标
x(:,time) =[x(1,time)+Deltalambda*cos(Jd(bestone,1)+Deltatheta);
x(2,time)+Deltalambda*sin(Jd(bestone,1)+Deltatheta)];
%更新坐标
Xs(time) = x(1,time);
Ys(time) = x(2,time);
Tes = [Tes,Jd(bestone,1)+Deltatheta];
Vs = [Vs,Deltalambda];
end
%画图
plot(x(1,time),x(2,time),'.')
hold on
drawnow;
if sqrt((Xs(time)-X_end)^2+(Ys(time)-Y_end)^2)<0.2
break;
end
end
4.仿真分析
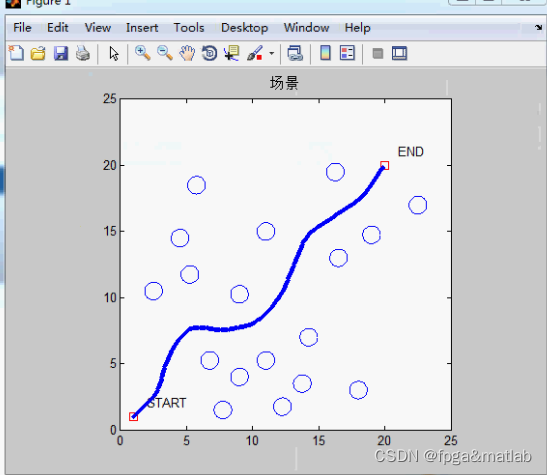
?

5.参考文献
[1]张素芹. 机器人BP神经网络避障控制模型构建及仿真[J]. 西安工业大学学报, 2015(8):678-682.A05-48
