一、机器学习中的优化思想

模型训练的目标：求解一组最适合的权重向量，令神经网络的输出结果与真实值尽量接近。

关键概念：损失函数是可以衡量真实值与预测结果的差异，评价模型学习过程中产生的损失的函数。

如果损失函数的值很小，则说明模型预测与真实值很接近，模型在数据集上表现优异，权重优秀；如果顺势函数的值很大，则说明模型预测值与真实值差异很大，模型在数据集上表现很差，权重糟糕。

二、回归：误差平方和SSE

在这里插入图片描述

from torch.nn import MSELoss
import torch

torch.random.manual_seed(420)
yhat = torch.randn(size=(50, 1), dtype=torch.float32)
y = torch.randn(size=(50, 1), dtype=torch.float32)

criterion = MSELoss() #实例化
loss = criterion(yhat, y)
#由于没有设定随机种子，所以每次运行的数字都不同
print(loss)
#tensor(2.4869)

对于MESloss来说，有一个重要的参数是reduction，reduction默认是mean，求得是平均损失，reduction设置为sum时，求的是全部样本的损失值之和。

criterion_1 = MSELoss(reduction='sum')
loss_1 = criterion_1(yhat, y)
print(loss_1)
#tensor(124.3458)
criterion_2 = MSELoss(reduction='mean')
loss_2 = criterion_2(yhat, y)
print(loss_2)
#tensor(2.4869)

三、二分类交叉熵损失函数

在这里插入图片描述

1 极大似然估计求解二分类交叉熵损失

在这里插入图片描述

我们将极大似然概率公式表示为：
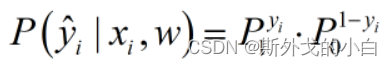
在这里插入图片描述
第i个样本预测为1的概率为p1，被预测为0的概率为p0，yi代表第i个样本的真实标签，这个标签为1的时候，p1就保留下来了，如果真实标签为0的话，p0就保留下来了。然后我们使得这个预测概率达到最大即可。
在这里插入图片描述

2 用tensor实现二分类交叉熵损失

N = 3 * pow(10, 3)
torch.random.manual_seed(420)
x = torch.rand((N, 4), dtype=torch.float32)
w = torch.rand((4, 1), dtype=torch.float32)
y = torch.randint(low=0, high=2, size=(N, 1), dtype=torch.float32)

zhat = torch.mm(x, w)
sigma = torch.sigmoid(zhat)

loss = (-1/N) * torch.sum(y * torch.log(sigma) + (1 - y) * torch.log(1 - sigma))
print(loss)

注意，在深度学习pytorch框架下，尽量使用torch中的函数，这样的话，计算速度较快

案例比较

N = 3 * pow(10, 6)
torch.random.manual_seed(420)
x = torch.rand((N, 4), dtype=torch.float32)
w = torch.rand((4, 1), dtype=torch.float32)
y = torch.randint(low=0, high=2, size=(N, 1), dtype=torch.float32)

zhat = torch.mm(x, w)
sigma = torch.sigmoid(zhat)

starttime = time.time()
loss_1 = (-1/N) * torch.sum(y * torch.log(sigma) + (1 - y) * torch.log(1 - sigma))
endtime = time.time()
print(endtime - starttime)
#0.02230215072631836

starttime = time.time()
loss_2 = (-1/N) * sum(y * torch.log(sigma) + (1 - y) * torch.log(1 - sigma))
endtime = time.time()
print(endtime - starttime)
#17.05457043647766

通过这两个例子可以看出，使用torch.sum()的计算速度远远比python自带的sum()要快得多

3 用PyTorch中的类实现二分类交叉熵损失

BCEWithLogitsLoss以及BCELoss
其中BCEWithLogitsLoss自带sigmoid函数，只需要输入预测值zhat即可
对于BCELoss来说，需要输入激活函数激活后的sigma

在N = 3 * pow(10, 6)
torch.random.manual_seed(420)
x = torch.rand((N, 4), dtype=torch.float32)
w = torch.rand((4, 1), dtype=torch.float32)
y = torch.randint(low=0, high=2, size=(N, 1), dtype=torch.float32)
zhat = torch.mm(x, w)
sigma = torch.sigmoid(zhat)

#调用nn模块下的类
criterion = nn.BCELoss()
LOSS = criterion(sigma, y)
print(LOSS)
#tensor(0.8685)
criterion2 = nn.BCEWithLogitsLoss()#实例化
loss2 = criterion2(zhat, y)
print(loss2)
#tensor(0.8685)

四、多分类交叉熵损失函数

1 由二分类推广到多分类

假设样本的真实标签为1，我们就希望p1最大，同理，如果样本的真实标签为其他值，我们就希望其他的值对应的概率最大。
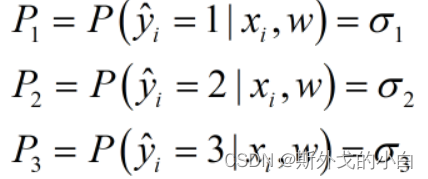
在这里插入图片描述
但是在二分类问题中，我们将y和1-y作为概率p的指数，这是因为真实标签只有0和1两种状况，但是在多分类中，我们的真实标签可能是任意整数，无法使用y的1-y这样的机构来构建似然函数，所以我们认为，如果多分类的标签也可以用0和1来表示就好了，这样我们就可以继续使用真实标签作为指数的方式。

因此我们对标签进行了one-hot编码，如下所示：
在这里插入图片描述
在矩阵中，
每一行依旧对应样本，但却由三分类衍生出了三个新的列，分别代表：真实标签是否等于1、等于2以及等于3。把标签整合为标签矩阵后，我们就可以将单个样本在总共k个分类情况整合为以下的似然函数：
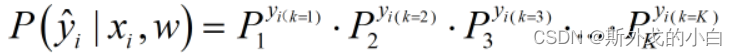
在这里插入图片描述
j为样本i所对应的真实标签的编号
虽有所有训练集的样本来说，我们可以定义如下等式来表达所有样本在特征张量X和权重向量w组成的预测函数中，预测出所有可能的预测值yhat的概率p为：

与二分类问题一致，似然函数解出来以后，我们对似然函数求对数得到：
在这里插入图片描述
这个函数就是交叉熵损失函数，不难看出，二分类交叉熵函数是多分类的一种特殊情况

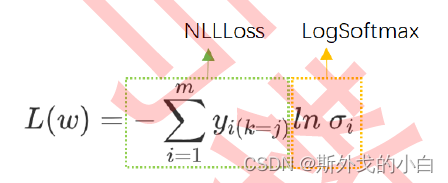
在pytorch里面直通通过nn.logsoftmax类调用这个功能，我们把对数之外的：乘以标签、加和、取负等等过程打包起来，称之为负对数似然函数（Negative Log Likelihood function），也就是说，在计算损失函数时，我们就不再需要单独的softmax函数了。

2 用PyTorch实现多分类交叉熵损失

在pytorch中实现交叉熵函数的时候，有两种方法：

调用logsoftmax和NLLLoss实现

N = 3*pow(10, 2)
torch.random.manual_seed(420)
X = torch.rand((N, 4), dtype=torch.float32)
w = torch.rand((4, 3), dtype=torch.float32, requires_grad=True)
y = torch.randint(low=0, high=3, size=(N,), dtype=torch.float32)

zhat = torch.mm(X, w)
#从这里开始调用softmax和NLLLoss
logsm = nn.LogSoftmax(dim=1) #实例化
logsigma = logsm(zhat)
criterion = nn.NLLLoss() #实例化
#由于交叉熵损失需要将标签转化为独热形式，因此不接受浮点数作为标签的输入
#对NLLLoss而言，需要输入logsigma
criterion(logsigma, y.long())
#tensor(1.1591, grad_fn=<NllLossBackward0>)

直接调用CrossEntropyLoss（）

N = 3*pow(10, 2)
torch.random.manual_seed(420)
X = torch.rand((N, 4), dtype=torch.float32)
w = torch.rand((4, 3), dtype=torch.float32, requires_grad=True)
y = torch.randint(low=0, high=3, size=(N,), dtype=torch.float32)

zhat = torch.mm(X, w)
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(zhat, y.long())
print(loss)
#tensor(1.1591, grad_fn=<NllLossBackward0>)