数据挖掘2.5——聚类
1.聚类分析概述
■ 定义
? 把数据对象集合按照相似性划分成多个子集的过程
? 每个子集是一个簇 (cluster) , 使得簇中的对象
彼此相似,但与其他簇中的对象不相似。
■ 与分类的区别
无监督学习,给的数据没有类标号信息
2.基本聚类方法
2.1 划分方法
■ 定义
将有n 个对象的数据集D划分成k个簇,并且k<n,满足如下的要求:
? 每个簇至少包含一个对象
? 每个对象属于且仅属于一个簇
■ 基本思想
? 首先创建一个初始k划分( k为要构造的划分数)
? 然后不断迭代地计算各个簇的聚类中心并依新的聚类中心调整聚类情况,直至收敛
■ 目标
? 同一个簇中的对象之间尽可能“接近” 或相关
? 不同簇中的对象之间尽可能“远离” 或不同
■ 适用性
? 这些启发式算法适合发现中小规模数据库中的球状聚
? 对于大规模数据库和处理任意形状的聚类, 这些算法需要进一步扩展
1.Kmeans算法
Kmeans算法为启发式算法,遵循的寻优原则:每次聚类保证局部最优,随后调整聚类,利用局部最优聚类的上限来不断逼近全局最优。
实例1
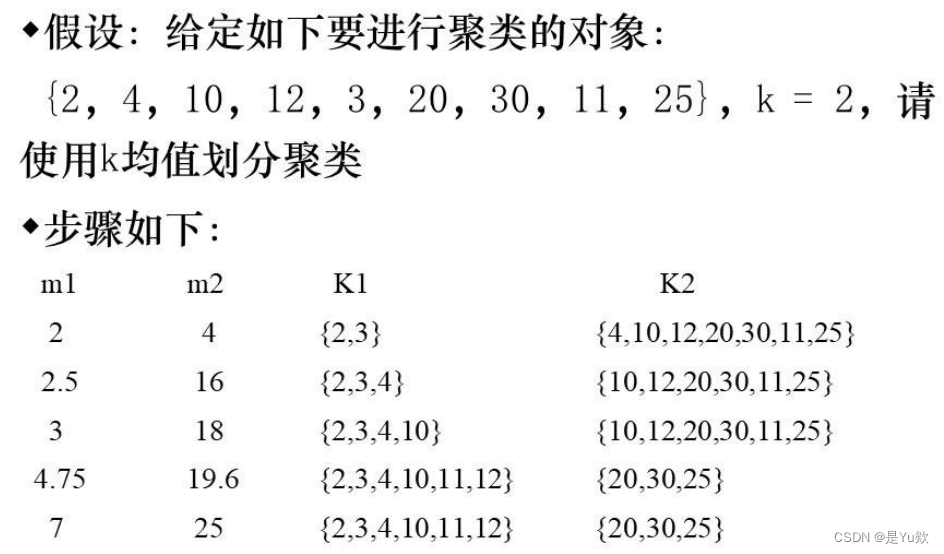
其中,m1,m2为两个聚类的中心坐标。
■ 优点
? 聚类时间快
? 当结果簇是密集的,而簇与簇之间区别明显时, 效果较好
? 相对可扩展和有效, 能对大数据集进行高效划分
■ 缺点
? 用户必须事先指定聚类簇的个数
? 常常终止于局部最优
? 只适用于数值属性聚类(计算均值有意义)
? 对噪声和异常数据也很敏感
? 不同的初始值, 结果可能不同
? 不适合发现非凸面形状的簇
■ 问题
1.初始簇影响
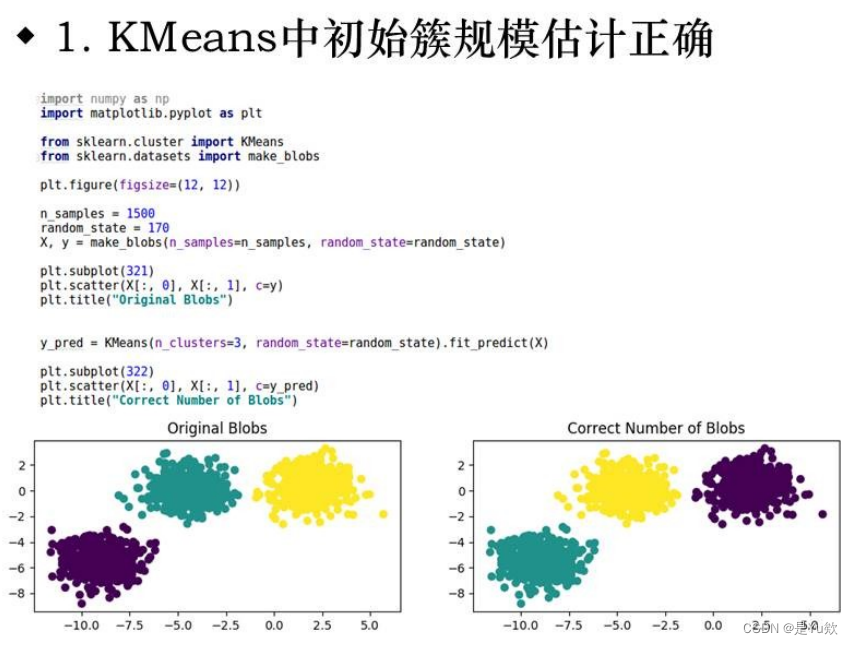
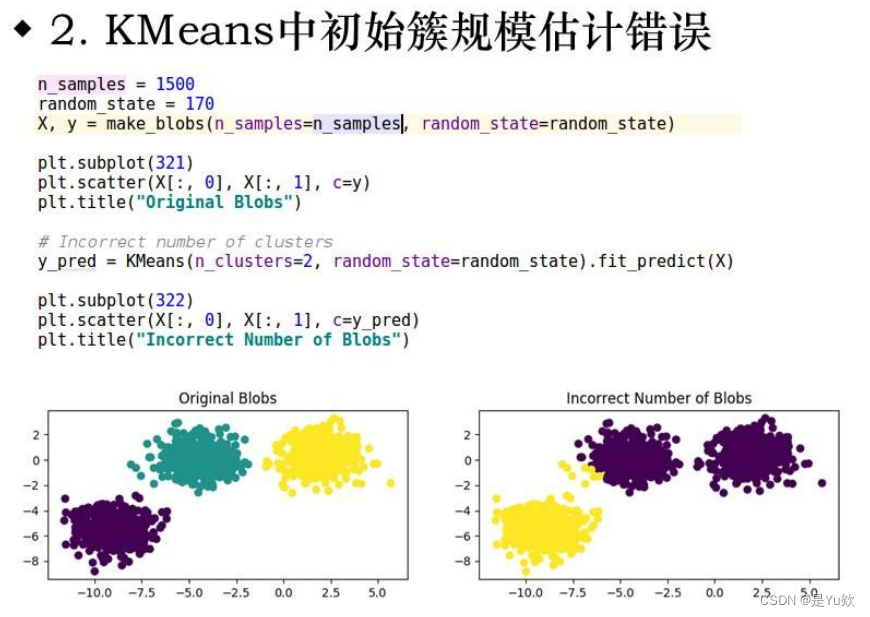
2.数据分布形状
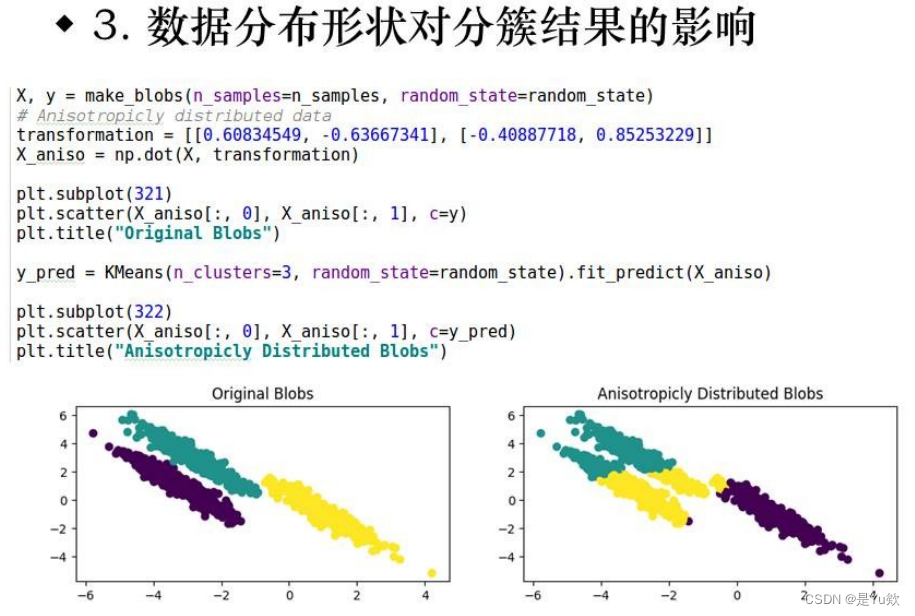
3.数据分散程度
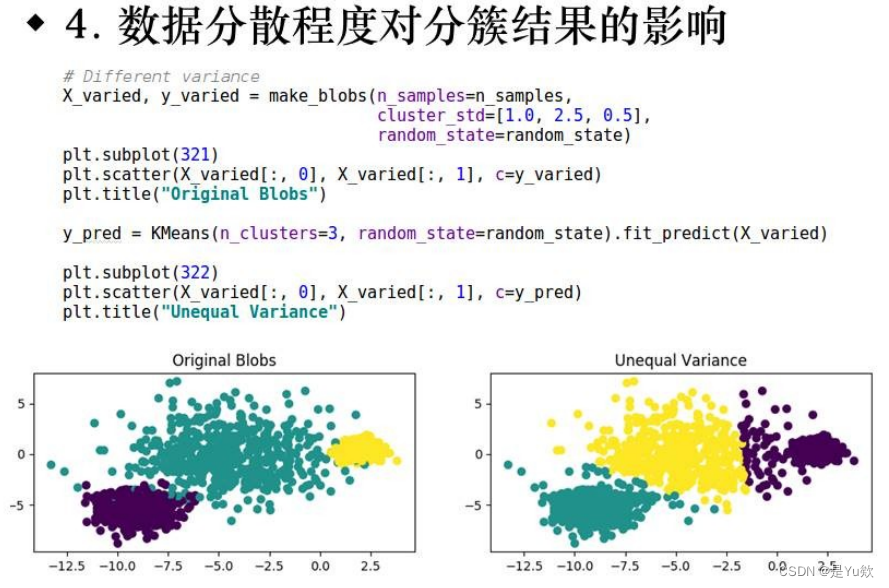
4.初始随机种子的影响
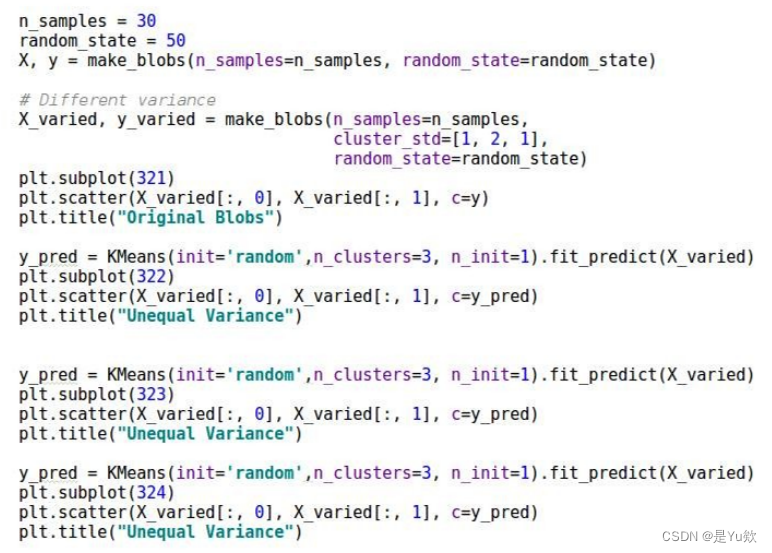
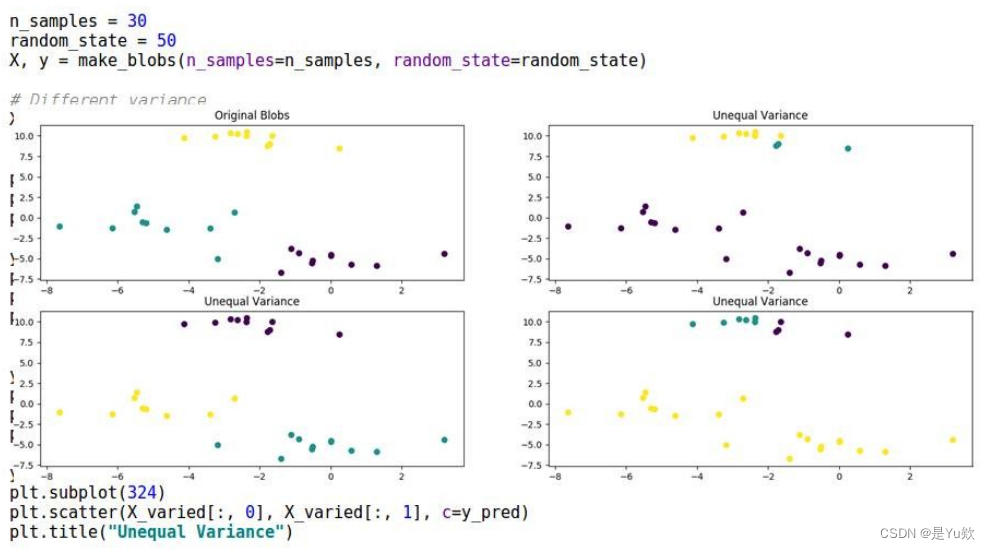
2.k-modes算法
解决数据敏感问题
3.KMeans++算法
每次选择一个与聚类中心距离最大的点作为新的聚类中心。
KMeans++效果:解决初始点选择问题。
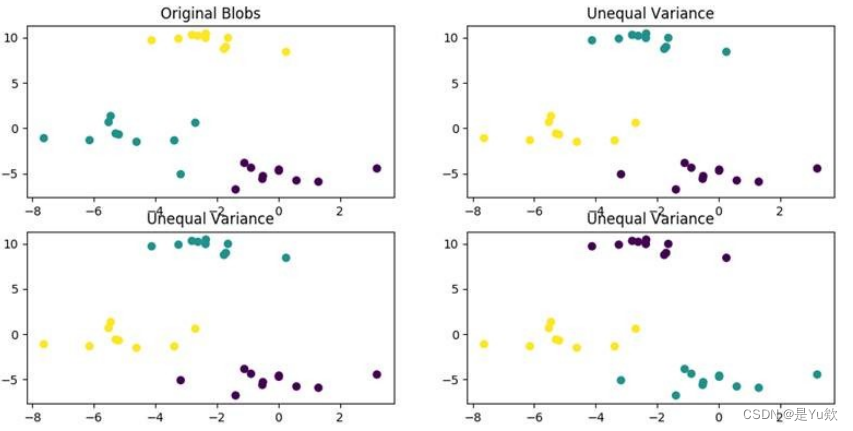
4.k-中心点
选择簇中位置最中心的实际对象为中心点,基于最小化所有对象与其的相异度之和来划分。
优点:解决对离群值敏感的问题。
划分方法聚类质量评价准则:最小化E值。
基本思想
? 首先为每个簇随意选择一个代表对象,剩余的对象根据其与代表对象的距离分配给最近的一个簇
? 然后迭代地用非代表对象来替代代表对象,以改进聚类的质量(找更好的代表对象)
? 聚类结果的质量用一个代价函数来估算,该函数评估了对象与其参照对象之间的平均相异度
PAM算法实例

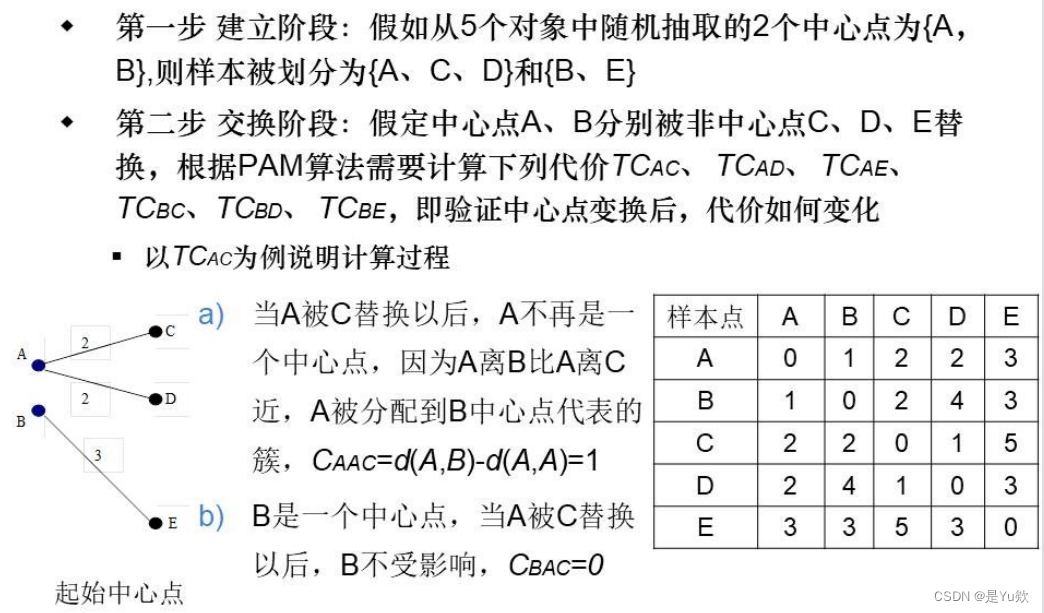
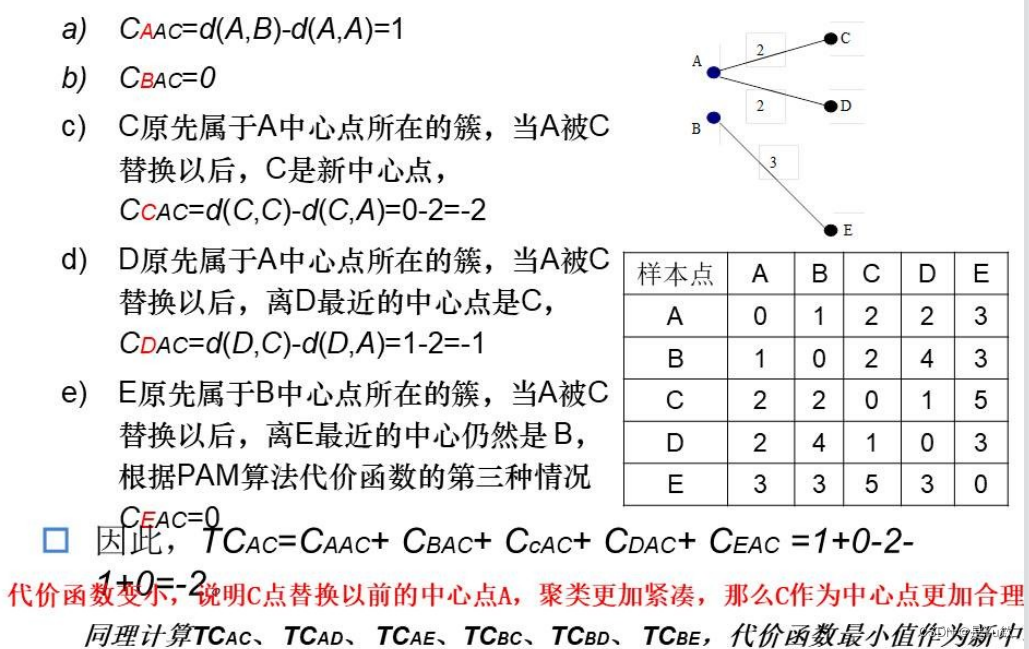
2.2 层次方法
2.3基于密度的方法
根据密度条件对邻近对象分组形成簇,簇的增长或者根据邻域密度,或者根据特定的密度函数(只要临近区域的密度超过某个阈值,就继续聚类)。
■ 主要特点
? 发现任意形状的聚类
? 处理噪音
? 一遍扫描
? 需要密度参数作为终止条件
■ 缺点
对用户定义的参数是敏感的,参数难以确定(特别是对于高维数据),设置的细微不同可能导致差别很大的聚类。全局密度参数不能刻画内在的聚类结构。
3.聚类评估
估计在数据集上进行聚类的可行性,和被聚类方法产生的结果的质量。
■ 聚类评估的任务
? 估计聚类趋势:评估数据集是否存在非随机结构。
? 确定数据集中的簇数:在聚类之前,估计簇数。
? 测定聚类质量:聚类之后,评估结果簇的质量。
