如有错误,恳请指出。
文章目录
在上一篇博文笔记中,见:【35】Sequence序列网络介绍与使用,我介绍了如何利用pytorch提供的RNN与LSTM接口,来搭建一个时序网络,那么在这篇文章中就打算用RNN网络或者LSTM网络来做一些时序预测的相关任务。
这里提供了两个例子:
- 1)使用RNN网络来预测正弦方波
- 2)使用LSTM网络来预测周期性的航班数据
其中,第一个例子是龙曲良老师授课的一个例子,第二个例子是见博客修改的,见参考资料。
在下篇文章中,还会介绍一下LSTM的其他我觉得挺好玩的应用:
- 3)使用LSTM网络来对文本分类
- 4)使用LSTM网络来对图像分类
- 5)使用LSTM网络来生成手写数字图像
1. 时序预测任务——使用RNN网络来预测正弦方波
这里设置一个简单的任务就是使用使用rnn来预测正弦曲线
1.1 导入工具包
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from matplotlib import pyplot as plt
- 设置的相关信息,取消科学计数法输出
np.set_printoptions(suppress=True)
1.2 超参数设置
num_time_steps = 50
input_size = 1
hidden_size = 16
output_size = 1
lr=0.01
1.3 模型定义
这里我设置了一个单层的RNN网络来预测下一个时序节点的波形,最后的波形预测用一个全连接层来实现。
class Net(nn.Module):
def __init__(self, ):
super(Net, self).__init__()
self.rnn = nn.RNN(
input_size=input_size,
hidden_size=hidden_size,
num_layers=1,
batch_first=True,
)
for p in self.rnn.parameters():
nn.init.normal_(p, mean=0.0, std=0.001)
self.linear = nn.Linear(hidden_size, output_size)
def forward(self, x, hidden_prev):
out, hidden_prev = self.rnn(x, hidden_prev)
# [b, seq, h]
out = out.view(-1, hidden_size)
out = self.linear(out)
out = out.unsqueeze(dim=0)
return out, hidden_prev
1.4 模型训练
model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr)
hidden_prev = torch.zeros(1, 1, hidden_size)
for iter in range(6000):
# 随机从0-3区间中挑选一个数值
start = np.random.randint(3, size=1)[0]
# 在区间中间隔采样50(num_time_steps)个数据点
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)
output, hidden_prev = model(x, hidden_prev)
hidden_prev = hidden_prev.detach()
loss = criterion(output, y)
model.zero_grad()
loss.backward()
# for p in model.parameters():
# print(p.grad.norm())
# torch.nn.utils.clip_grad_norm_(p, 10) # 梯度裁剪
optimizer.step()
if iter % 100 == 0:
print("Iteration: {} loss {}".format(iter, loss.item()))
训练结果输出:
Iteration: 0 loss 0.6180879473686218
Iteration: 100 loss 0.002067530993372202
Iteration: 200 loss 0.0033898595720529556
Iteration: 300 loss 0.0028499257750809193
Iteration: 400 loss 0.0016402869950979948
Iteration: 500 loss 0.0015365825966000557
Iteration: 600 loss 0.0007872747373767197
Iteration: 700 loss 0.0013388539664447308
Iteration: 800 loss 0.0009592065471224487
Iteration: 900 loss 0.00023990016779862344
Iteration: 1000 loss 0.0014855732442811131
Iteration: 1100 loss 0.0005326495738700032
Iteration: 1200 loss 0.0006256766500882804
Iteration: 1300 loss 0.0013620775425806642
Iteration: 1400 loss 0.0010062839137390256
Iteration: 1500 loss 0.0011015885975211859
Iteration: 1600 loss 2.126746221620124e-05
Iteration: 1700 loss 0.000390108791179955
Iteration: 1800 loss 0.0016134703764691949
Iteration: 1900 loss 0.001025702222250402
Iteration: 2000 loss 0.0015523084439337254
Iteration: 2100 loss 0.0003646172699518502
Iteration: 2200 loss 0.000642314029391855
Iteration: 2300 loss 0.0004722262092400342
Iteration: 2400 loss 5.732586942031048e-05
Iteration: 2500 loss 0.0013018838362768292
Iteration: 2600 loss 0.0008787440019659698
Iteration: 2700 loss 0.0009332495392300189
Iteration: 2800 loss 0.0007348429062403738
Iteration: 2900 loss 0.0004210669139865786
Iteration: 3000 loss 0.0004240694979671389
Iteration: 3100 loss 0.0005803901003673673
Iteration: 3200 loss 0.00195941049605608
Iteration: 3300 loss 8.851500751916319e-05
Iteration: 3400 loss 0.00030293306917883456
Iteration: 3500 loss 0.00031553610460832715
Iteration: 3600 loss 0.00031228255829773843
Iteration: 3700 loss 0.00039033975917845964
Iteration: 3800 loss 0.00020553779904730618
Iteration: 3900 loss 0.0011390189174562693
Iteration: 4000 loss 0.00015774763596709818
Iteration: 4100 loss 7.591523899463937e-05
Iteration: 4200 loss 8.699461614014581e-05
Iteration: 4300 loss 0.0004444770747795701
Iteration: 4400 loss 0.0004794316191691905
Iteration: 4500 loss 0.00047654256923124194
Iteration: 4600 loss 0.0002331874711671844
Iteration: 4700 loss 0.0003834210510831326
Iteration: 4800 loss 0.0005701710470020771
Iteration: 4900 loss 0.00010284259042236954
Iteration: 5000 loss 5.453555058920756e-05
Iteration: 5100 loss 0.00043016314157284796
Iteration: 5200 loss 0.00013311025395523757
Iteration: 5300 loss 0.0003936859138775617
Iteration: 5400 loss 0.0002417201321804896
Iteration: 5500 loss 0.00017509324243292212
Iteration: 5600 loss 0.00017528091848362237
Iteration: 5700 loss 0.00040555483428761363
Iteration: 5800 loss 0.000313715310767293
Iteration: 5900 loss 9.533046249998733e-05
1.5 模型测试
start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)
predictions = []
input = x[:, 0, :]
for _ in range(x.shape[1]):
input = input.view(1, 1, 1)
(pred, hidden_prev) = model(input, hidden_prev)
input = pred
predictions.append(pred.detach().numpy().ravel()[0])
x = x.data.numpy().ravel()
y = y.data.numpy()
plt.scatter(time_steps[:-1], x.ravel(), s=90)
plt.plot(time_steps[:-1], x.ravel())
plt.scatter(time_steps[1:], predictions)
plt.show()
输出的可视化结果:

1.6 完整代码
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from matplotlib import pyplot as plt
num_time_steps = 50
input_size = 1
hidden_size = 16
output_size = 1
lr = 0.01
class Net(nn.Module):
def __init__(self, ):
super(Net, self).__init__()
self.rnn = nn.RNN(
input_size=input_size,
hidden_size=hidden_size,
num_layers=1,
batch_first=True,
)
for p in self.rnn.parameters():
nn.init.normal_(p, mean=0.0, std=0.001)
self.linear = nn.Linear(hidden_size, output_size)
def forward(self, x, hidden_prev):
out, hidden_prev = self.rnn(x, hidden_prev)
# [b, seq, h]
out = out.view(-1, hidden_size)
out = self.linear(out)
out = out.unsqueeze(dim=0)
return out, hidden_prev
model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr)
hidden_prev = torch.zeros(1, 1, hidden_size)
# 为什么可以做的一个思考:
# 此时模型为当前的每一个输入都进行了一个输出,维度是一样的,也就是为每一个输入预测了一个输出
# 而这个输出与下一个时序就构成了损失,可以用一个损失函数就这个过程构建一个损失函数即可训练
for iter in range(6000):
start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)
# output是包含了每一个样本的一个输出值,可以考虑最后的一个输出值hidden_prev,也可以考虑整个的输出值
# 这里就是使用后者整个的时序样本的隐藏单元都作为一个训练样本
output, hidden_prev = model(x, hidden_prev)
hidden_prev = hidden_prev.detach()
# 损失函数的构建
loss = criterion(output, y)
model.zero_grad()
loss.backward()
# for p in model.parameters():
# print(p.grad.norm())
# torch.nn.utils.clip_grad_norm_(p, 10)
optimizer.step()
if iter % 100 == 0:
print("Iteration: {} loss {}".format(iter, loss.item()))
start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)
predictions = []
input = x[:, 0, :]
for _ in range(x.shape[1]):
input = input.view(1, 1, 1)
(pred, hidden_prev) = model(input, hidden_prev) # 这里的hidden_prev是训练过程中的隐藏单元
input = pred # 当前的输入作为下一层的输入,不断的进行实现时序预测
predictions.append(pred.detach().numpy().ravel()[0]) # 只通过一个输入,就可以连续不断的进行预测
# 可视化展示,这里的y其实是没什么用的
x = x.data.numpy().ravel()
y = y.data.numpy()
plt.scatter(time_steps[:-1], x.ravel(), s=90)
plt.plot(time_steps[:-1], x.ravel())
plt.scatter(time_steps[1:], predictions)
plt.show()
2. 时序任务预测——使用LSTM网络来预测周期性的航班数据
2.1 导入工具包
from sklearn.preprocessing import MinMaxScaler
import torch
import torch.nn as nn
import seaborn as sns
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
2.2 数据可视化
- 查看数据集的表格
flight_data = sns.load_dataset("flights")
flight_data.head()
| year | month | passengers | |
|---|---|---|---|
| 0 | 1949 | Jan | 112 |
| 1 | 1949 | Feb | 118 |
| 2 | 1949 | Mar | 132 |
| 3 | 1949 | Apr | 129 |
| 4 | 1949 | May | 121 |
- 查看数据集的图像波形
fig_size = plt.rcParams["figure.figsize"]
fig_size[0] = 15
fig_size[1] = 5
plt.rcParams["figure.figsize"] = fig_size
plt.title('Month vs Passenger')
plt.ylabel('Total Passengers')
plt.xlabel('Months')
plt.grid(True)
plt.autoscale(axis='x',tight=True)
plt.plot(flight_data['passengers'])
plt.show()

2.3 数据预处理
- 构建训练数据与测试数据
all_data = flight_data['passengers'].values.astype(float)
test_data_size = 12
train_data = all_data[:-test_data_size]
test_data = all_data[-test_data_size:]
print(len(train_data))
print(len(test_data))
132
12
- 归一化处理
# 使用最小/最大标量(最小值和最大值分别为-1和1)对数据进行规范化
scaler = MinMaxScaler(feature_range=(-1, 1))
# 这里因为只能对一列进行处理,所以涉及一些维度的转变
train_data_normalized = scaler.fit_transform(train_data .reshape(-1, 1))
# 将数据集转换为张量,然后将列再重新打平处理
train_data_normalized = torch.FloatTensor(train_data_normalized).view(-1)
2.4 构建数据集
# 创建用于训练的序列和相应的标签
train_window = 12
def create_inout_sequences(input_data, tw):
inout_seq = []
L = len(input_data)
for i in range(L-tw):
train_seq = input_data[i:i+tw]
train_label = input_data[i+tw:i+tw+1]
inout_seq.append((train_seq ,train_label))
return inout_seq
train_inout_seq = create_inout_sequences(train_data_normalized, train_window)
2.5 模型创建
这里普通搭建了一个单层的LSTM网络来预测时序数据
class LSTM(nn.Module):
def __init__(self, input_size=1, hidden_layer_size=200, output_size=1):
super().__init__()
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_layer_size, num_layers=1)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size),
torch.zeros(1, 1, self.hidden_layer_size))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq, self.hidden_cell)
predictions = self.linear(lstm_out.view(lstm_out.size(0), -1))
return predictions[-1]
model = LSTM()
print(model)
seq, labels = train_inout_seq[0]
print("seq.shape:{}, labels.shape:{}".format(seq.shape, labels.shape))
model(seq[:,None,None]).shape
输出结果
LSTM(
(lstm): LSTM(1, 200)
(linear): Linear(in_features=200, out_features=1, bias=True)
)
torch.Size([12]) torch.Size([1])
torch.Size([1])
2.6 模型训练
model = LSTM()
loss_function = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
epochs = 200
for i in range(epochs):
for seq, labels in train_inout_seq:
optimizer.zero_grad()
model.hidden_cell = (torch.zeros(1, 1, model.hidden_layer_size),
torch.zeros(1, 1, model.hidden_layer_size))
y_pred = model(seq[:,None,None])
single_loss = loss_function(y_pred, labels)
single_loss.backward()
optimizer.step()
if i%25 == 0 or i == (epochs-1):
print(f'epoch: {i:3} loss: {single_loss.item():10.8f}')
print("-"*80)
print("train sucess, loss:{}".format(single_loss))
epoch: 0 loss: 0.08318637
epoch: 24 loss: 0.00497702
epoch: 49 loss: 0.00723564
epoch: 74 loss: 0.00158882
epoch: 99 loss: 0.00002601
epoch: 124 loss: 0.00142831
epoch: 149 loss: 0.00005675
epoch: 174 loss: 0.00011440
epoch: 199 loss: 0.00020664
--------------------------------------------------------------------------------
train sucess, loss:0.0002066389424726367
2.7 模型测试
fut_pred = 12
test_inputs = train_data_normalized[-train_window:].tolist()
len(test_inputs), train_data_normalized.shape
# 输出: (12, torch.Size([132]))
model.eval()
# 预测十二个数值
for i in range(fut_pred):
#不断取出列表的最后12个数值来喂入模型,获取输出
seq = torch.FloatTensor(test_inputs[-train_window:])
with torch.no_grad():
model.hidden = (torch.zeros(1, 1, model.hidden_layer_size),
torch.zeros(1, 1, model.hidden_layer_size))
pred = model(seq[:,None,None]).item()
test_inputs.append(pred)
print('i:{}, pred:{}'.format(i, pred))
i:0, pred:0.454874724149704
i:1, pred:0.5675606727600098
i:2, pred:0.8822157979011536
i:3, pred:0.781266987323761
i:4, pred:0.5928680896759033
i:5, pred:0.5053937435150146
i:6, pred:0.7401428818702698
i:7, pred:1.0358431339263916
i:8, pred:1.2730270624160767
i:9, pred:1.2577072381973267
i:10, pred:1.681006669998169
i:11, pred:1.2105796337127686
转换为归一化前的数值
# 将预测出来的数据进行反归一化处理,同样的这里需要将其转换为列数据才可以反归一化转化
actual_predictions = scaler.inverse_transform(np.array(test_inputs).reshape(-1, 1))
actual_predictions.flatten().tolist()
[360.0000016912818,
342.0000002216548,
406.0000023394823,
396.00000293552876,
420.0000015050173,
472.00000518560415,
548.0000006556511,
559.0,
463.00000572204596,
407.00000227987766,
362.0000015720725,
405.00000239908695,
434.98399974405766,
460.6200530529023,
532.2040940225124,
509.2382396161557,
466.37749040126806,
446.47707664966583,
499.88250562548643,
567.1543129682541,
621.1136566996574,
617.6283966898918,
713.9290174245834,
606.9068666696548]
2.8 可视化展示
x = np.arange(120, 144, 1)
print(x)
plt.title('Month vs Passenger')
plt.ylabel('Total Passengers')
plt.grid(True)
plt.autoscale(axis='x', tight=True)
plt.plot(flight_data['passengers'])
plt.plot(x,actual_predictions)
plt.show()
[120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
138 139 140 141 142 143]
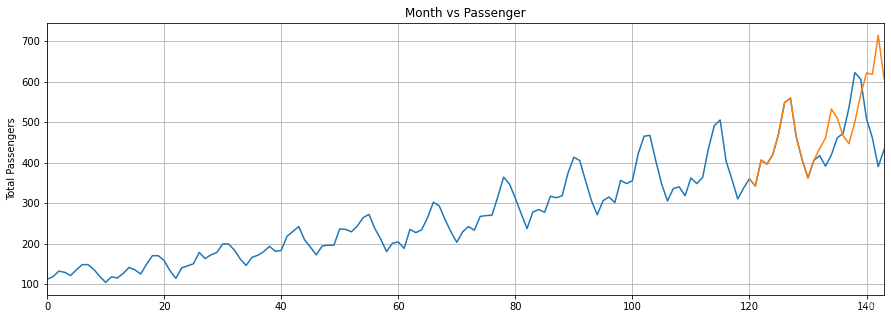
这里可以看出来,可以预测部分数据,但是显然预测的准确性不是很高,但是后面有回落的势头,所以基本的波形还是可以预测的
总结:
这里其实可以看见,在rnn与lstm训练时序数据的时候,可以有两种训练方式。
- 第一种是利用整段序列的下一个时间戳整段预测输出来与整段序列的真实标签来进行批量训练
- 第二种是利用整段序列的下一个时间戳最后一个预测点来与时间戳的样本真实点来进行单个训练
这两种方法,在上诉的两个例子中分别使用了一个,都是可行的。
参考资料:
