一、图像分割
1.图像分割：根据图像的某些局部特征（灰度级、纹理、彩色或统计特征等）的相似性和互斥性，将图像分割成若干子区域，在每个子区域内部具有相似（相同或相近）特性，而相邻子区域的特性互斥。所以图像分割是利用图像局部特征的相似性和互斥性。
2.图像分割方法分类（灰度图）：一类是利用区域间灰度的突变性，确定区域的边界或边缘的位置，即边缘检测法；零一类是利用区域内灰度的相似性将图像像素点分成若干相似的区域，称为区域生长法。
二、基于边缘点检测的图像分割
0.边缘点检测的基本原理
边缘点检测就是确定图像中有无边缘点，若有还要进一步确定其位置。
步骤如下：
首先对图像中每一个像素施以检测算子，然后根据实现确定的准则对检测算子的输出进行判定，确定该像素点是否为边缘点；
剔除某些边界点或填补边缘间断点，并将这些边缘连接成线。
边缘检测，即检测灰度级或者结构具有突变的地方，表明一个区域的终结，也是另一个区域开始的地方。这种不连续性称为边缘。不同的图像灰度不同，边界处一般有明显的边缘，利用此特征可以分割图像。图像中边缘处像素的灰度值不连续，这种不连续性可通过求导数来检测到。对于阶跃状边缘，其位置对应一阶导数的极值点，对应二阶导数的过零点(零交叉点)。因此常用微分算子进行边缘检测。本次实验采用Roberts算子、Prewitt算子、Sobel算子和各向同性Sobel算子进行边缘检测。
1.Roberts算子
Roberts算子是一种利用局部差分算子寻找边缘的算子，采用对角方向相邻两像素之差，故也被称为四分差分法，其水平方向与垂直方向梯度定义为：
水平方向与垂直方向的模板为：
用4点进行差分，以求得梯度，方法简单。其缺点是对噪声较敏感，常用于不含噪声的图像边缘点检测。
2.Prewitt算子
因为平均能减少或消除噪声， Prewitt梯度算子法就是先求平均，再求差分来求梯度。水平和垂直梯度模板分别为：
利用检测模板可求得水平和垂直方向的梯度，再通过梯度合成和边缘点判定，就可得到平均差分法的检测结果。可以消除噪声的影响。
3.Sobel算子
Sobel算子就是对当前行或列对应的值加权后，再进行平均和差分，也称为加权平均差分。水平和垂直梯度模板分别为：
Sobel算子和Prewitt算子一样，都在检测边缘点的同时具有抑制噪声的能力，检测出的边缘宽度至少为二像素。由于它们都是先平均后差分，平均时会丢失一些细节信息，使边缘有一定的模糊。但由于Sobel算子的加权作用，其使边缘的模糊程度要稍低于Prewitt算子。
代码如下：
自己实现：
F = imread(‘4.2.07.tiff’);
F = rgb2gray(F);
f=double(F);
[m,n]=size(f);
g=zeros(m,n);
for i=2:m-1
for j=2:n-1 DX=(f(i+1,j-1)-f(i-1,j-1))+2*(f(i+1,j)-f(i-1,j))+(f(i+1,j+1)-f(i-1,j+1)); DY=(f(i-1,j+1)-f(i-1,j-1))+2*(f(i,j+1)-f(i,j-1))+(f(i+1,j+1)-f(i+1,j-1));
g(i,j)=round(sqrt(DXDX+DYDY));
end
end
G=uint8(g);
也可以使用内置函数实现：
function [ G ] = Sobel( F )
%Sobel算子
if size(F,3)>1
F = rgb2gray(F);
end
F = im2double(F);
mBlock = fspecial(‘sobel’);
mImgDy = imfilter(F, mBlock, ‘replicate’);
mImgDx = imfilter(F, mBlock’,‘replicate’);
G = sqrt(mImgDy.*mImgDy+mImgDx.*mImgDx);
end
直接使用内置edge函数：
F = imread(‘4.2.07.tiff’);
F = rgb2gray(F);
G=edge(F,‘sobel’);
4.各向同性Sobel算子
Sobel算子的水平和垂直梯度分别对水平及垂直方向的突变敏感，即只有用其检测水平及垂直走向的边缘时，梯度的幅度才一样，Frei和Chen曾提出上、下、左、右权值由2改为根号2，可以使水平、垂直和对角边缘的梯度相同，即为各向同性的Sobel算子，其水平和垂直梯度的模板为：
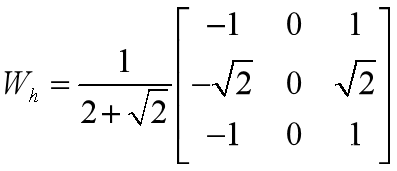
各向同性Sobel算子和普通Sobel算子相比，位置加权系数更为准确，在检测不同方向的边缘时梯度的幅度一致。
代码如下：
function [G] = IsotropicSobel(F)
%各向同性Sobel算子
f=double(F);
[m,n]=size(f);
g=zeros(m,n);
for i=2:m-1
for j=2:n-1
DX=(f(i+1,j-1)-f(i-1,j-1))+2^0.5*(f(i+1,j)-f(i-1,j))+(f(i+1,j+1)-f(i-1,j+1)); DY=(f(i-1,j+1)-f(i-1,j-1))+2^0.5*(f(i,j+1)-f(i,j-1))+(f(i+1,j+1)-f(i+1,j-1)); g(i,j)=round(sqrt(DXDX+DYDY)*4/(2+2^0.5));
end
end
G=uint8(g);
end
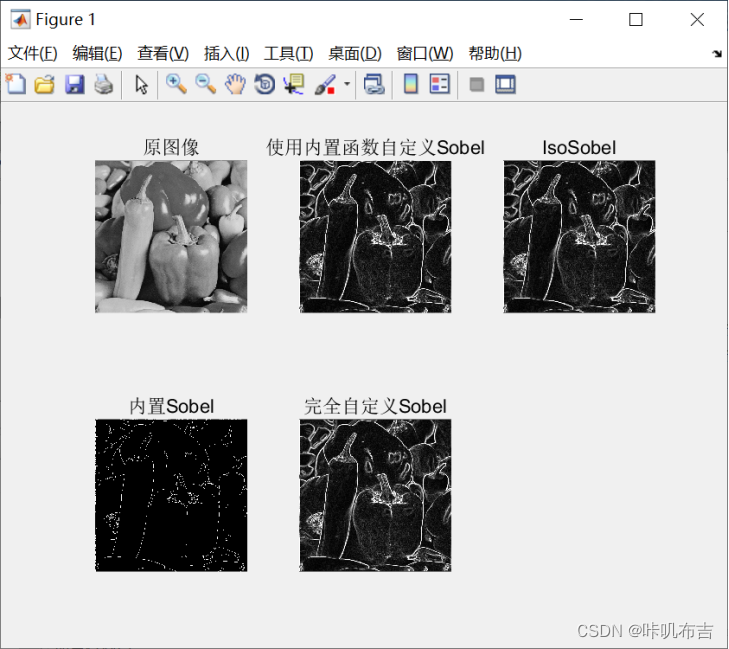
5.分析与比较
以下三幅图是使用不同数据进行处理的结果，可以看出Prewitt算子和Sobel算子优于 Roberts算子，因为它们具有减少噪声的能力，但是边缘更模糊，而Sobel算子又较Prewitt算子边缘模糊程度低。各向同性Sobel又较普通Sobel算子检测效果更好。
但是不知道为什么我自己写的与内置边缘检测函数差异较大。
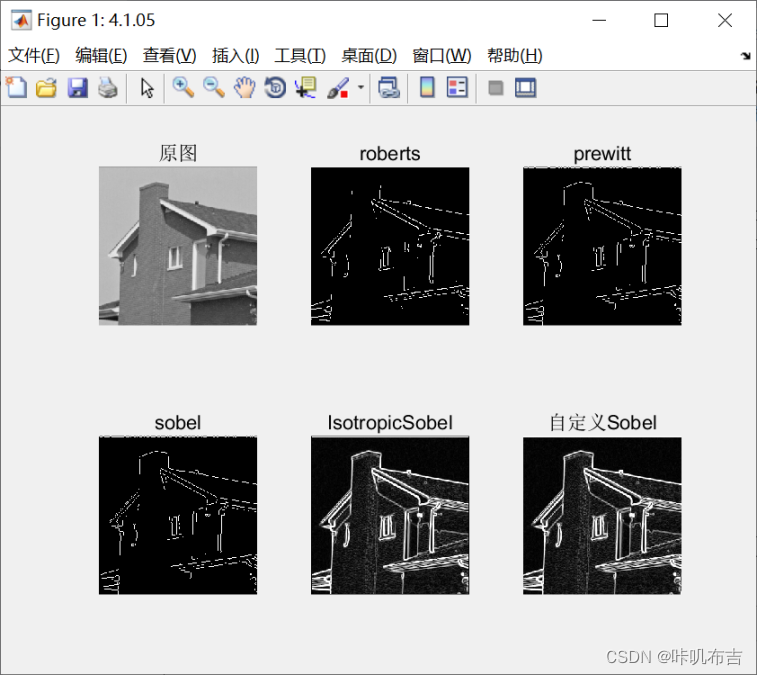
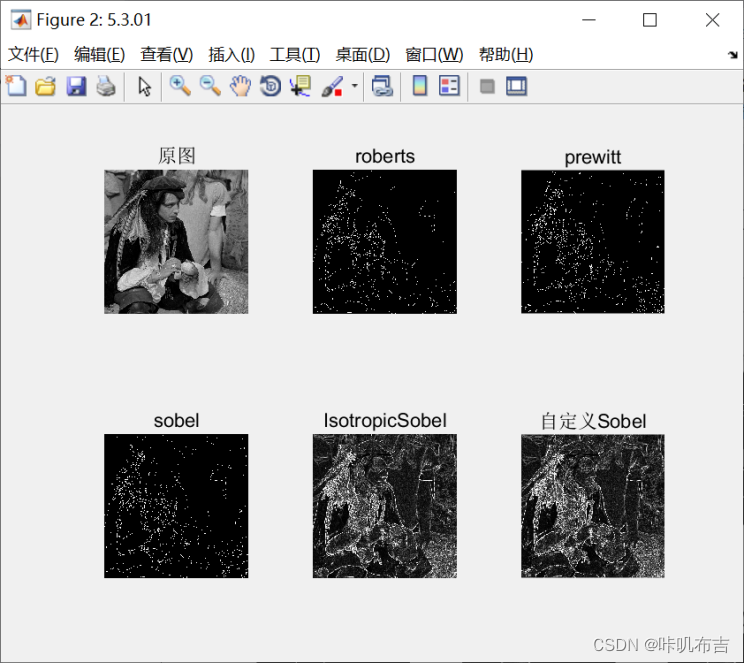
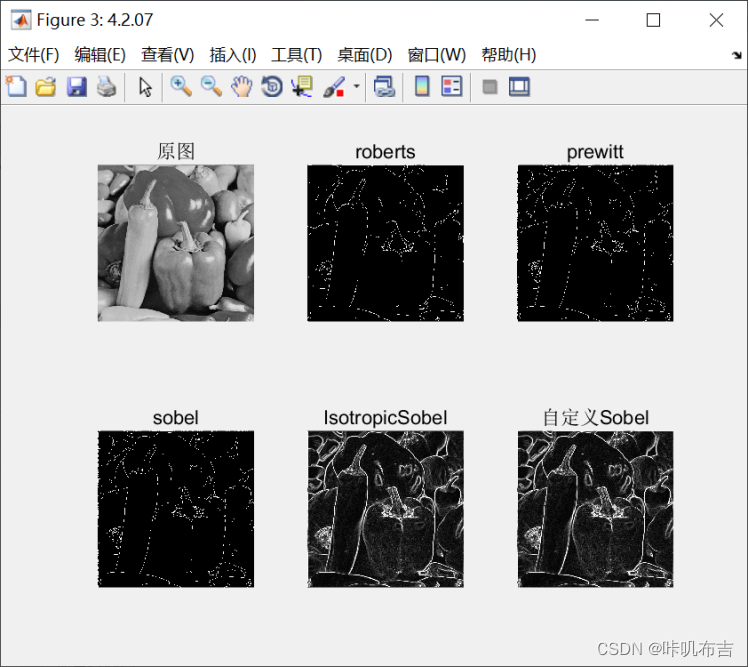
这是单Sobel算子采用不同方式实现的对比图，我并没有看出Sobel与各向同性Sobel算子分割有什么区别。
三、区域分割法
0.区域分割的基本原理
区域分割法就是利用同一区域内灰度值的相似性，将相似的区域合并，把不相似区域分开，最终形成不同的分割区域。常用的区域分割方法有区域生长法、分裂合并法及空间聚类法等几种方法。
区域生长是把图像分割成特征相似的若干小区域，比较相邻小区域的特征，若相似则合并为同一区域，如此进行直到不能合并为止，最后生成特征不同的各区域。这种分割方法也称为区域扩张法。
方法步骤：
(1)确定要分割的区域数目，并在每个区域选择或确定一个能正确代表该区域灰度取值的像素点，称为种子点 。
(2)选择有意义特征和邻域方式。
(3)确定相似性准则。
1.简单生长（像素＋像素）
按事先确定的相似性准则,生长点（种子点为第一个生长点）接收（合并）其邻域（比如4邻域）的像素点，该区域生长。接收后的像素点称为生长点，其值取种子点的值。重复该过程，直到不能生长为止，到此该区域生成。
简单生长法的相似性准则为：
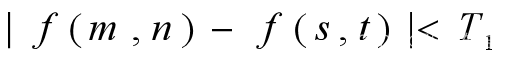
其中f(s,t)为生长点(s,t)的灰度值，f(m,n)为(s,t)的邻域点(m,n)的灰度值，T1为相似门限。f(s,t)始终取种子点的值，因此这种方法对种子点的依赖性强。
代码如下：
function J = SimpleRegionGrow(I, init_pos, reg_maxdist)
% 简单生长法
% 输入：
% I : 二维数组，数值表示灰度值，0~255
% init_pos: 指定的种子点坐标
% reg_maxdist : 阈值
% 输出：
% J : 感兴趣区域
[row, col] = size(I); % 输入图像的维数
J = zeros(row, col); % 输出
x0 = init_pos(1); % 初始点
y0 = init_pos(2);
init=I(x0,y0);
J(x0, y0) = 1; % 生长起始点设置为白色
reg_num = 1; % 符合生长条件的点的个数
count = 1; % 每次判断周围八个点中符合条件的数目
reg_choose = zeros(row*col, 2); % 记录已选择点的坐标
reg_choose(reg_num, 😃 = init_pos;
num = 1; % 第一个点
while count > 0
s_temp = 0; % 周围八个点中符合条件的点的灰度值总和
count = 0;
for k = 1 : num % 对新增的每个点遍历，避免重复
i = reg_choose(reg_num - num + k, 1);
j = reg_choose(reg_num - num +k, 2);
if J(i, j) == 1 && i > 1 && i < row && j > 1 && j < col % 已确定且不是边界上的点
% 八邻域
for u = -1 : 1
for v = -1 : 1
% 未处理且满足生长条件的点
if J(i + u, j + v) == 0 && abs(I(i + u, j + v) - init) <= reg_maxdist
J(i + u, j + v) = 1; % 对应点设置为白色
count = count + 1;
reg_choose(reg_num + count, 😃 = [i + u, j + v];
s_temp = s_temp + I(i + u, j + v); % 灰度值存入s_temp中
end
end
end
end
end
num = count; % 新增的点
reg_num = reg_num + count; % 区域内总点数
end
end
2.质心生长法（区域＋像素）
修改简单生长法的相似性准则，即相似性准则变为：
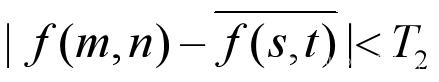
这里的是已生长区域内所有像素（所有生长点）的灰度平均值。即用已生成区域的像素灰度均值（类似质心）作为基准，这样就可以克服简单生长法中过分依赖种子点的缺陷。
代码如下：
function [ J ] = CentroidGrowthMethod( I, init_pos, reg_maxdist )
% 质心生长法
% 输入：
% I : 二维数组，数值表示灰度值，0~255
% init_pos: 指定的种子点坐标
% reg_maxdist : 阈值
% 输出：
% J : 感兴趣区域
[row, col] = size(I); % 输入图像的维数
J = zeros(row, col); % 输出
x0 = init_pos(1); % 初始点
y0 = init_pos(2);
reg_mean = I(x0, y0); % 生长起始点灰度值
J(x0, y0) = 1; % 生长起始点设置为白色
reg_sum = reg_mean; % 符合生长条件的灰度值总和
reg_num = 1; % 符合生长条件的点的个数
count = 1; % 每次判断周围八个点中符合条件的数目
reg_choose = zeros(row*col, 2); % 记录已选择点的坐标
reg_choose(reg_num, 😃 = init_pos;
num = 1; % 第一个点
while count > 0
s_temp = 0; % 周围八个点中符合条件的点的灰度值总和
count = 0;
for k = 1 : num % 对新增的每个点遍历，避免重复
i = reg_choose(reg_num - num + k, 1);
j = reg_choose(reg_num - num +k, 2);
if J(i, j) == 1 && i > 1 && i < row && j > 1 && j < col % 已确定且不是边界上的点
% 八邻域
for u = -1 : 1
for v = -1 : 1
% 未处理且满足生长条件的点
if J(i + u, j + v) == 0 && abs(I(i + u, j + v) - reg_mean) <= reg_maxdist
J(i + u, j + v) = 1; % 对应点设置为白色
count = count + 1;
reg_choose(reg_num + count, 😃 = [i + u, j + v];
s_temp = s_temp + I(i + u, j + v); % 灰度值存入s_temp中
end
end
end
end
end
num = count; % 新增的点
reg_num = reg_num + count; % 区域内总点数
reg_sum = reg_sum + s_temp; % 区域内总灰度值
reg_mean = reg_sum / reg_num; % 区域灰度平均值
end
end
3.混合生长法（区域＋区域）
混和生长法是按相似性准则进行相邻区域的合并，即相似性准则是相邻两区域的灰度均值相近，即
其中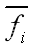
和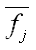
分别为相邻的第i区域和第j区域的灰度平均值。这样，就用某像素点周围区域的灰度平均值来表示该点的特性，增加了抗干扰性。
4.分析与比较
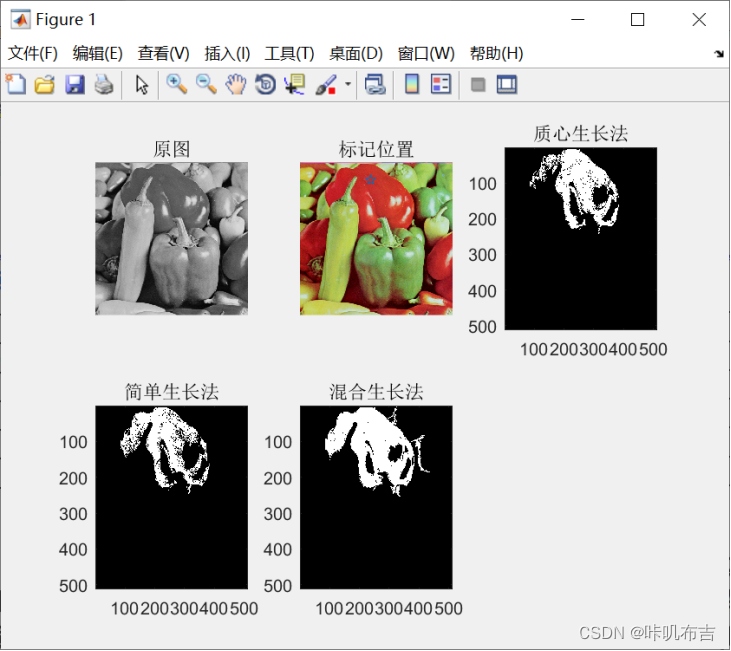
总的来说，质心生长法优于简单生长法，因为取均值可以减少对种子点的依赖。
四、附录
CentroidGrowthMethod.m
function [ J ] = CentroidGrowthMethod( I, init_pos, reg_maxdist )
% 质心生长法
% 输入：
% I : 二维数组，数值表示灰度值，0~255
% init_pos: 指定的种子点坐标
% reg_maxdist : 阈值
% 输出：
% J : 感兴趣区域
[row, col] = size(I); % 输入图像的维数
J = zeros(row, col); % 输出
x0 = init_pos(1); % 初始点
y0 = init_pos(2);
reg_mean = I(x0, y0); % 生长起始点灰度值
J(x0, y0) = 1; % 生长起始点设置为白色
reg_sum = reg_mean; % 符合生长条件的灰度值总和
reg_num = 1; % 符合生长条件的点的个数
count = 1; % 每次判断周围八个点中符合条件的数目
reg_choose = zeros(row*col, 2); % 记录已选择点的坐标
reg_choose(reg_num, :) = init_pos;
num = 1; % 第一个点
while count > 0
s_temp = 0; % 周围八个点中符合条件的点的灰度值总和
count = 0;
for k = 1 : num % 对新增的每个点遍历，避免重复
i = reg_choose(reg_num - num + k, 1);
j = reg_choose(reg_num - num +k, 2);
if J(i, j) == 1 && i > 1 && i < row && j > 1 && j < col % 已确定且不是边界上的点
% 八邻域
for u = -1 : 1
for v = -1 : 1
% 未处理且满足生长条件的点
if J(i + u, j + v) == 0 && abs(I(i + u, j + v) - reg_mean) <= reg_maxdist
J(i + u, j + v) = 1; % 对应点设置为白色
count = count + 1;
reg_choose(reg_num + count, :) = [i + u, j + v];
s_temp = s_temp + I(i + u, j + v); % 灰度值存入s_temp中
end
end
end
end
end
num = count; % 新增的点
reg_num = reg_num + count; % 区域内总点数
reg_sum = reg_sum + s_temp; % 区域内总灰度值
reg_mean = reg_sum / reg_num; % 区域灰度平均值
end
end
IsotropicSobel.m
function [G] = IsotropicSobel(F)
%各向同性Sobel算子
% 输入：灰度图像
% 输出：分割后的图像
f=double(F);
[m,n]=size(f);
g=zeros(m,n);
for i=2:m-1
for j=2:n-1
DX=(f(i+1,j-1)-f(i-1,j-1))+2^0.5*(f(i+1,j)-f(i-1,j))+(f(i+1,j+1)-f(i-1,j+1));
DY=(f(i-1,j+1)-f(i-1,j-1))+2^0.5*(f(i,j+1)-f(i,j-1))+(f(i+1,j+1)-f(i+1,j-1));
g(i,j)=round(sqrt(DX*DX+DY*DY)*4/(2+2^0.5));
end
end
G=uint8(g);
end
MixRegionGrow.m
function J = regionGrow(I,init_pos,threshold)
% 混合区域
%
% 输入：I - 原图像
% 输出：J - 输出图像
if isinteger(I)
I=im2double(I);
end
[M,N]=size(I);
x0 = init_pos(1);
y0 = init_pos(2);
x1=round(x0); %横坐标取整
y1=round(y0); %纵坐标取整
seed=I(x1,y1); %将生长起始点灰度值存入seed中
J=zeros(M,N); %作一个全零与原图像等大的图像矩阵J，作为输出图像矩阵
J(x1,y1)=1; %将J中与所取点相对应位置的点设置为白
sum=seed; %储存符合区域生长条件的点的灰度值的和
suit=1; %储存符合区域生长条件的点的个数
count=1; %记录每次判断一点周围八点符合条件的新点的数目
threshold=20; %阈值，注意需要和double类型存储的图像相符合
while count>0
s=0; %记录判断一点周围八点时，符合条件的新点的灰度值之和
count=0;
for i=1:M
for j=1:N
if J(i,j)==1
if (i-1)>0 && (i+1)<(M+1) && (j-1)>0 && (j+1)<(N+1) %判断此点是否为图像边界上的点
for u= -1:1 %判断点周围八点是否符合阈值条件
for v= -1:1
if J(i+u,j+v)==0 && abs(I(i+u,j+v)-seed)<=threshold && 1/(1+1/15*abs(I(i+u,j+v)-seed))>0.8
J(i+u,j+v)=1;
%判断是否尚未标记，并且为符合阈值条件的点
%符合以上两条件即将其在J中与之位置对应的点设置为白
count=count+1;
s=s+I(i+u,j+v); %此点的灰度之加入s中
end
end
end
end
end
end
end
suit=suit+count; %将n加入符合点数计数器中
sum=sum+s; %将s加入符合点的灰度值总合中
seed=sum/suit; %计算新的灰度平均值
end
offical.m
I1 = imread('4.1.05.tiff');
I1 =rgb2gray(I1);
% Roberts算子边缘检测
BW1=edge(I1,'roberts');
% Prewitt算子边缘检测
BW2=edge(I1,'prewitt');
% Sobel算子边缘检测
BW3=edge(I1,'sobel');
BW4=IsotropicSobel(I1);
BW5=Sobel(I1);
figure('name','4.1.05');
subplot(231),imshow(I1),title('原图');
subplot(232),imshow(BW1,[]),title('roberts');
subplot(233),imshow(BW2,[]),title('prewitt');
subplot(234),imshow(BW3,[]),title('sobel');
subplot(235),imshow(BW4),title('IsotropicSobel');
subplot(236),imshow(BW5),title('自定义Sobel');
I2 = imread('5.3.01.tiff');
% Roberts算子边缘检测
BW1=edge(I2,'roberts');
% Prewitt算子边缘检测
BW2=edge(I2,'prewitt');
% Sobel算子边缘检测
BW3=edge(I2,'sobel');
BW4 = IsotropicSobel(I2);
BW5 = Sobel(I2);
figure('name','5.3.01');
subplot(231),imshow(I2),title('原图');
subplot(232),imshow(BW1,[]),title('roberts');
subplot(233),imshow(BW2,[]),title('prewitt');
subplot(234),imshow(BW3,[]),title('sobel');
subplot(235),imshow(BW4),title('IsotropicSobel');
subplot(236),imshow(BW5),title('自定义Sobel');
I3 = imread('4.2.07.tiff');
I3 =rgb2gray(I3);
% Roberts算子边缘检测
BW1=edge(I3,'roberts');
% Prewitt算子边缘检测
BW2=edge(I3,'prewitt');
% Sobel算子边缘检测
BW3=edge(I3,'sobel');
BW4=IsotropicSobel(I3);
BW5=Sobel(I3);
figure('name','4.2.07');
subplot(231),imshow(I3),title('原图');
subplot(232),imshow(BW1,[]),title('roberts');
subplot(233),imshow(BW2,[]),title('prewitt');
subplot(234),imshow(BW3,[]),title('sobel');
subplot(235),imshow(BW4),title('IsotropicSobel');
subplot(236),imshow(BW5),title('自定义Sobel');
RegionGrowAct.m
clc;
clear;
img = imread('4.2.07.tiff');
I = rgb2gray(img);
if( exist('x','var') == 0 && exist('y','var') == 0)
figure;
subplot(231),imshow(I);title('原图');
I = double(I);
[y,x] = getpts;%鼠标取点 回车确定
x1 = round(x(1));%选择种子点
y1 = round(y(1));
end
% 质心生长法
J1 = CentroidGrowthMethod(I, [x1, y1], 10);
% 简单生长法
J2 = SimpleRegionGrow(I, [x1, y1], 10);
% 混合生长法
J3=regionGrow(I,[x1,y1],10);
subplot(232),imshow(img),title('标记位置');
hold on
plot(y, x, 'p')
hold off;
subplot(233),imagesc(J1),title('质心生长法');
subplot(234),imagesc(J2),title('简单生长法');
subplot(235),imagesc(J3),title('混合生长法');
SimpleRegionGrow.m
function J = SimpleRegionGrow(I, init_pos, reg_maxdist)
% 简单生长法
% 输入：
% I : 二维数组，数值表示灰度值，0~255
% init_pos: 指定的种子点坐标
% reg_maxdist : 阈值
% 输出：
% J : 感兴趣区域
[row, col] = size(I); % 输入图像的维数
J = zeros(row, col); % 输出
x0 = init_pos(1); % 初始点
y0 = init_pos(2);
init=I(x0,y0);
J(x0, y0) = 1; % 生长起始点设置为白色
reg_num = 1; % 符合生长条件的点的个数
count = 1; % 每次判断周围八个点中符合条件的数目
reg_choose = zeros(row*col, 2); % 记录已选择点的坐标
reg_choose(reg_num, :) = init_pos;
num = 1; % 第一个点
while count > 0
s_temp = 0; % 周围八个点中符合条件的点的灰度值总和
count = 0;
for k = 1 : num % 对新增的每个点遍历，避免重复
i = reg_choose(reg_num - num + k, 1);
j = reg_choose(reg_num - num +k, 2);
if J(i, j) == 1 && i > 1 && i < row && j > 1 && j < col % 已确定且不是边界上的点
% 八邻域
for u = -1 : 1
for v = -1 : 1
% 未处理且满足生长条件的点
if J(i + u, j + v) == 0 && abs(I(i + u, j + v) - init) <= reg_maxdist
J(i + u, j + v) = 1; % 对应点设置为白色
count = count + 1;
reg_choose(reg_num + count, :) = [i + u, j + v];
s_temp = s_temp + I(i + u, j + v); % 灰度值存入s_temp中
end
end
end
end
end
num = count; % 新增的点
reg_num = reg_num + count; % 区域内总点数
end
end
Sobel.m
function [ G ] = Sobel( F )
%Sobel算子
% 输入：灰度图像
% 输出：分割后的图像
if size(F,3)>1
F = rgb2gray(F);
end
F = im2double(F);
mBlock = fspecial('sobel');
mImgDy = imfilter(F, mBlock, 'replicate');
mImgDx = imfilter(F, mBlock','replicate');
G = sqrt(mImgDy.*mImgDy+mImgDx.*mImgDx);
end
SobelCompare.m
F = imread('4.2.07.tiff');
F = rgb2gray(F);
G1 =IsotropicSobel(F);
G3 =Sobel(F);
G2=edge(F,'sobel');
f=double(F);
[m,n]=size(f);
g=zeros(m,n);
for i=2:m-1
for j=2:n-1
DX=(f(i+1,j-1)-f(i-1,j-1))+2*(f(i+1,j)-f(i-1,j))+(f(i+1,j+1)-f(i-1,j+1));
DY=(f(i-1,j+1)-f(i-1,j-1))+2*(f(i,j+1)-f(i,j-1))+(f(i+1,j+1)-f(i+1,j-1));
g(i,j)=round(sqrt(DX*DX+DY*DY));
end
end
G4=uint8(g);
figure;
subplot(2,3,1), imshow(F), title('原图像');
subplot(2,3,2), imshow(G3), title('使用内置函数自定义Sobel');
subplot(2,3,3), imshow(G1), title('IsoSobel');
subplot(2,3,4), imshow(G2), title('内置Sobel');
subplot(2,3,5), imshow(G4), title('完全自定义Sobel');
