paper: https://www.kdd.org/kdd2016/papers/files/rfp0191-wangAemb.pdf
2016 KDD | SDNE: Structural Deep Network Embedding
摘要
网络嵌入是学习网络中顶点的低维表示的一种重要方法,目的是获取和保留网络结构。现有的网络嵌套方法几乎都采用浅层模型。然而,由于底层网络结构复杂,浅层模型无法捕捉到高度非线性的网络结构,导致网络的次优表示。因此,如何找到一种既能有效捕捉高度非线性网络结构又能保持全局和局部结构的方法是一个开放而又重要的问题。为了解决这一问题,本文提出了一种结构化深度网络嵌入方法,即SDNE。更具体地说,提出了一个半监督深度模型,该模型具有多层非线性函数,从而能够捕捉高度非线性的网络结构。然后我们提出利用一阶和二阶邻近性来共同保留网络结构。
无监督利用二阶邻近性来获取全局网络结构。而在监督中使用一阶邻近度作为监督信息,以保持局部网络结构。通过在半监督深度模型中对它们进行联合优化,该方法既能保持局部网络结构,又能保持全局网络结构,对稀疏网络具有鲁棒性。我们在五个现实网络上进行了实验,包括一个语言网络,一个引文网络和三个社会网络。结果表明,与基线相比,该方法能较好地重构原始网络,在多标签分类、链接预测和可视化三种应用中均取得显著效果。
模型
SDNE利用一阶和二阶相似度来保留网络结构。 二阶相似度作为无监督部分被用来捕获全局结构。一阶相似度作为监督部分被用来捕获局部结构。通过利用半监督的深层模型联合优化以上两个目标可以保留局部和全局网络结构。
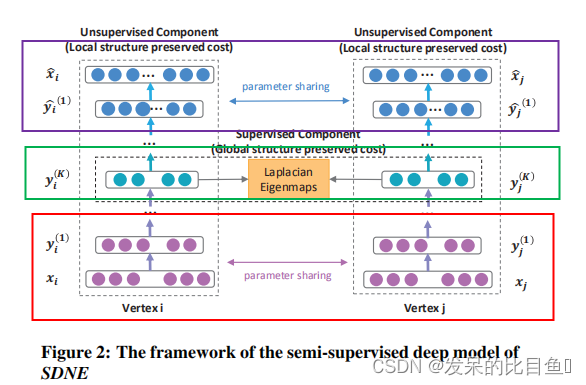
SDNE可以看成一个自编码器框架,上图中红框框部分可以看成编码器,中间绿色框框部分为编码器的输出,为节点的对应的嵌入向量,紫色框框部分为对应的解码器部分。了解了SDNE的框架组成部分之后,我们来看看各个部分是怎么设计的。
SDNE的无监督部分由深层自编码器组成。其中,编码器由多个非线性层组成,可以映射输入数据到表示空间。解码器也由多个非线性层组成。即,给定输入x,编码器每一隐藏层的输出如下:
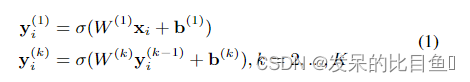
解码器重构输入
x
i
x_i
xi?为
x
^
\hat{x}
x^。因此
自编码器的目标就是最小化以下输出
x
^
\hat{x}
x^与原始输入
x
x
x的重构损失,损失函数如下:

如果使用邻接矩阵作为自编码器的输入
x
x
x,即每一行代表一个节点,因为邻接矩阵反应的是对应节点的邻居结构信息,这使得重构构成会使得有相似邻居结构的节点有相似的向量表示(即该无监督组件(自编码器)保留了网络中的二阶相似度信息)。但是,如果直接使用邻接矩阵S作为传统自编码器的输入,则模型更容易重构邻接矩阵中的零元素(因为网络的稀疏性,邻接矩阵中的零元素数目远远大于一的数目)。然而我们更关注的是邻接矩阵中代表邻居的1元素,为了解决这个问题,SDNE对非零元素的重构误差增加更多惩罚(即加了一个权重项bi,对非零元素的重构误差赋予更大的惩罚项)。新的目标函数(保留二阶相似度信息)如下:
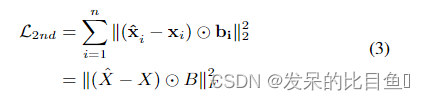
一个圈圈一个点的符号代表哈达玛积(矩阵对应位相乘),如果邻接矩阵
S
i
j
>
0
S_{ij}>0
Sij?>0,那么赋予相应的
b
i
j
=
1
b_{ij}=1
bij?=1,否则
b
i
j
=
β
>
1
b_{ij}=β>1
bij?=β>1,即更大的惩罚权重。以上便是SDNE的无监督模块,其通过二阶相似度试图保留全局网络结构。
然而,局部网络结构的保留也是必要的。以下介绍SDNE的用来保留一阶相似度的监督模块。 监督模块的一阶相似度的损失函数如下,这保证在原始网络中有连边的节点在嵌入空间中也比较相近(yi是对应的节点嵌入向量,即编码器的输出)。

SDNE总的目标函数如下(包含一阶相似度和二阶相似度):
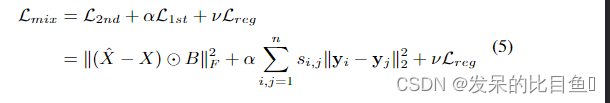
Lreg为L2正则项,惩罚神经网络的复杂性,防止模型过拟合,如下所示:
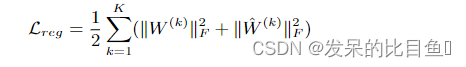

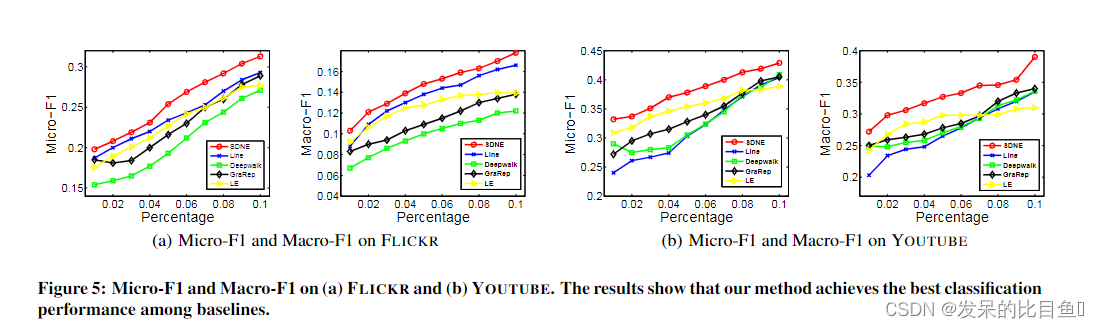
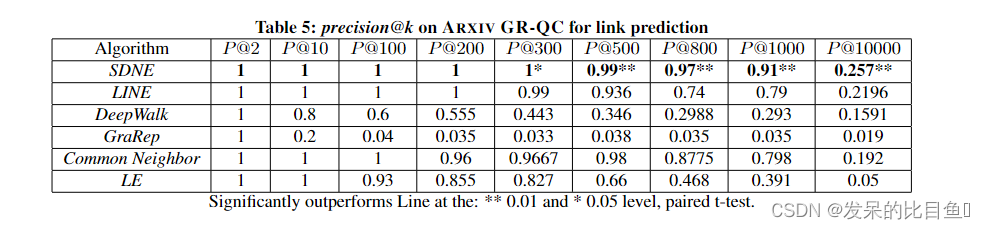
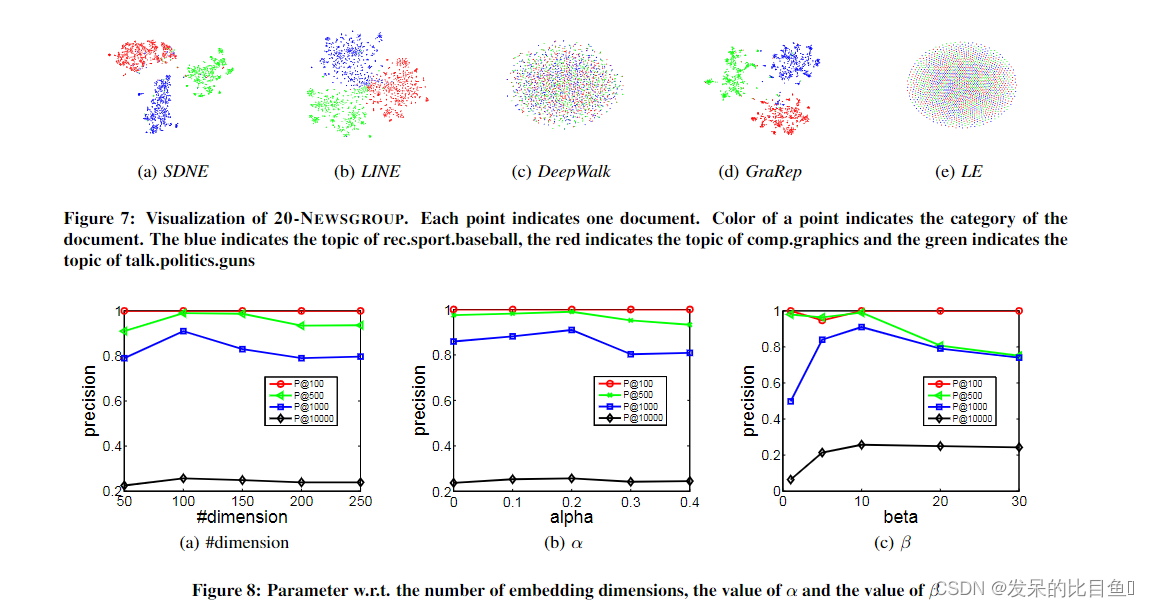
实验