DIN模型
论文地址:https://arxiv.org/pdf/1706.06978.pdf
提出DIN模型的原因:
当前CTR预估都是Embedding&MLP结构:高维稀疏输入特征按照特征组先映射成低维固定长度的embedding向量,然后拼接起来,喂给MLP网络中进行训练。这里面用户的向量表示因为是有限的固定长度,很难表示用户的多个兴趣。而在电子商务网站里面,用户可能同时对多个商品感兴趣。
在Embedding&MLP框架里面,用户的多个兴趣被压缩成一个固定有限长的向量,其实表达能力是受限的。一方面,不可能无限增大向量维度,因为可能产生过拟合,而且参数会变多,计算和存储耗时会让线上推断变的不可接受;另一方面,没有必要将所有兴趣压缩到一个相同的向量里面,因为用户的行为仅受到一部分兴趣影响,例如一个游泳爱好者点击泳镜,主要是因为上周买的泳装而不是上周买的鞋子。
论文提出的DIN能给定一个候选的item,考虑用户历史行为,自适应的计算用户的向量表示。与候选item相关性高的历史行为,对用户向量表示的贡献就大,反之就小,不同的候选item得到的用户向量不一样。
同时,还提出另外2个创新点。模型加入L2-norm,每个batch需要计算所有参数的正则结果,计算量非常大,论文提出在batch内,只对出现过的特征做正则,减少计算量。另外还提出了一个新的激活函数,是PReLU的泛化,对效果有帮助。
模型
特征输入
数据通常大多是分组的类别形式,如下,会通过one-hot或者multi-hot转变成高维稀疏的二值特征输入。
[weekday=Friday, gender=Female,visited_cate_ids={Bag,Book}, ad_cate_id=Book],
第
i
i
i个特征组编码后的向量表示为
t
i
∈
R
K
i
\mathbf t_i \in R^{K_i}
ti?∈RKi?,
K
i
K_i
Ki?表示特征i编码后的向量维度,即特征
i
i
i包含
K
i
K_i
Ki?个不同的id,
t
i
[
j
]
\mathbf t_i[j]
ti?[j]表示向量第
j
j
j维的值,
t
i
[
j
]
∈
{
0
,
1
}
\mathbf t_i[j] \in \{ 0,1\}
ti?[j]∈{0,1}
∑
j
=
1
K
i
=
k
\sum_{j=1}^{K_i} = k
∑j=1Ki??=k,当用one-hot编码,
k
=
1
k=1
k=1,当用multi-hot编码
k
>
1
k>1
k>1.
输入是由各个特征组的向量拼接起来的,假设有 M M M个特征组,则输入特征向量 x = [ t 1 , t 2 , . . . , t M ] \mathbf x = [\mathbf t_1, \mathbf t_2, ..., \mathbf t_M ] x=[t1?,t2?,...,tM?],输入特征向量的维度为 ∑ i = 1 M K i = K \sum_{i=1}^MK_i = K ∑i=1M?Ki?=K
上面的特征编码示例如下:
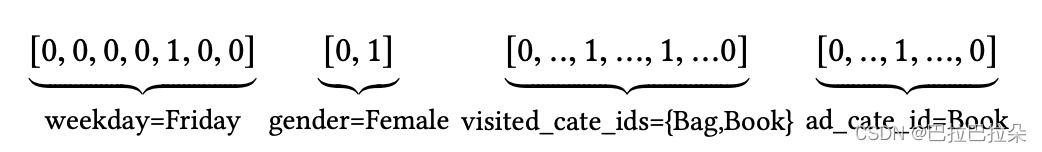
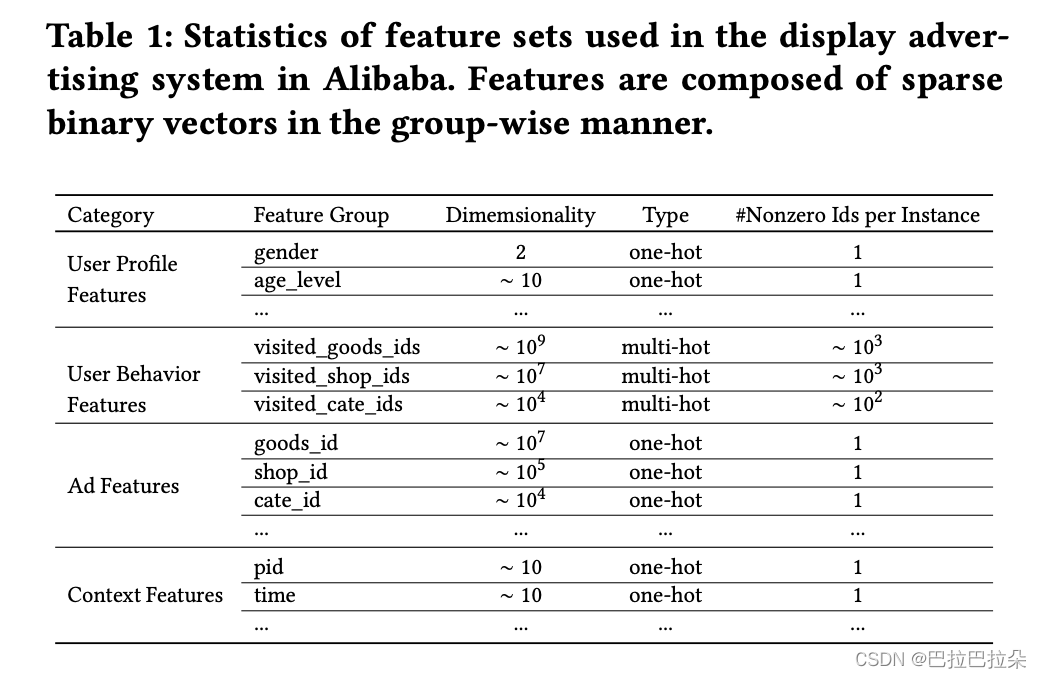
论文用到的特征有4类,如下,列举了每个特征的维度及编码类型。没有用交叉特征,用DNN来提取。
模型结构
先看下base模型
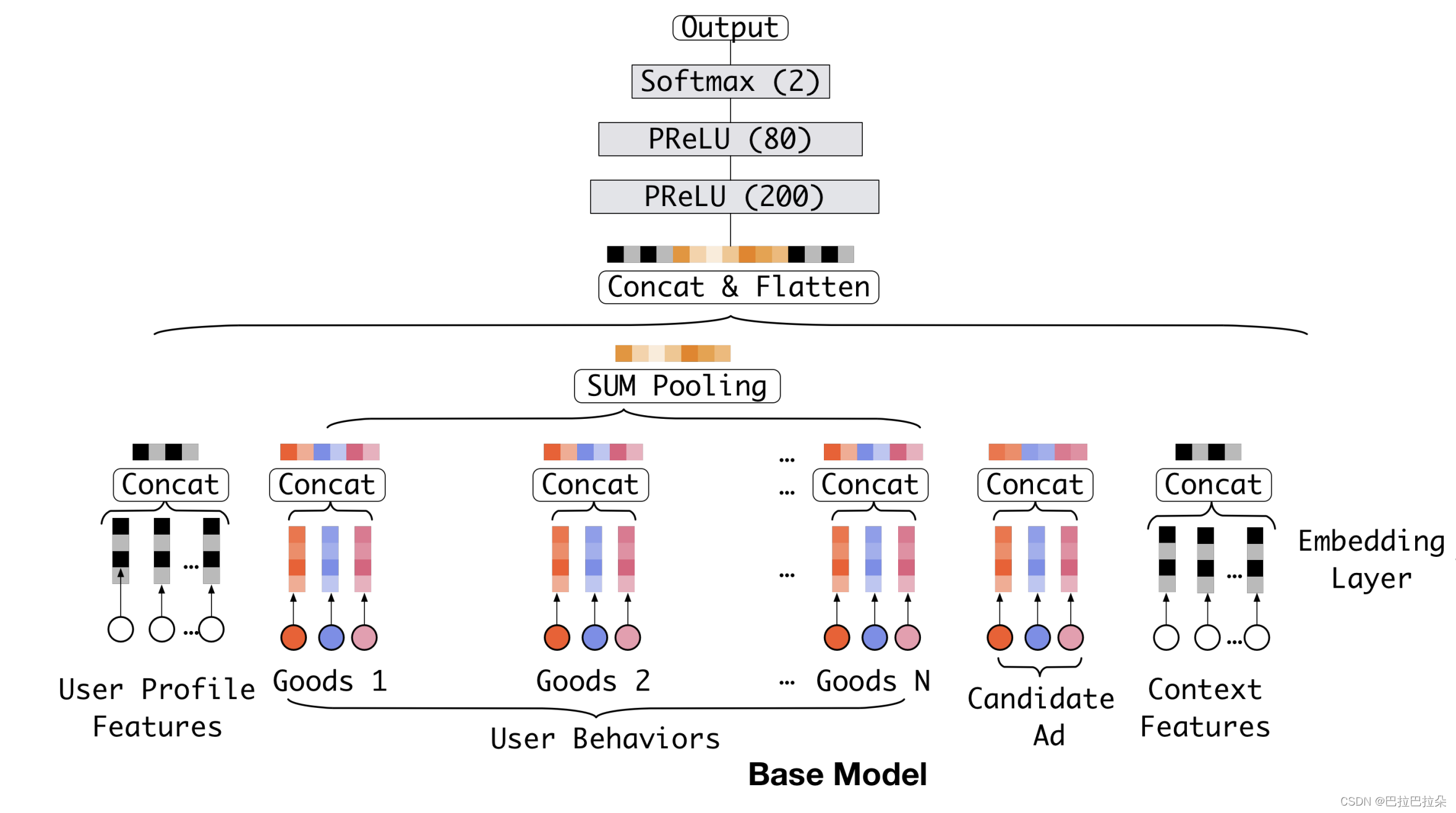
Embedding层
Embedding层是将高维稀疏输入向量转换为低维稠密输入向量。对于第 i i i个特征组的输入向量 t i \mathbf t_i ti?,Embedding转换词典 W i = [ w 1 i , w 2 i , . . . , w K i i ] ∈ R D × K i \mathbf W^i = [\mathbf w_1^i,\mathbf w_2^i, ..., \mathbf w_{K_i}^i ] \in R^{D \times K_i} Wi=[w1i?,w2i?,...,wKi?i?]∈RD×Ki?, w j i \mathbf w_j^i wji?表示维度为 D D D的Embedding向量。
若 t i \mathbf t_i ti?是one-hot向量时,当 t i [ j ] = 1 \mathbf t_i[j] = 1 ti?[j]=1,则第 i i i个特征组的输入向量 t i \mathbf t_i ti?的低维稠密向量表示 e i = w j i \mathbf e_i = \mathbf w_j^i ei?=wji?,是单个向量。
若 t i \mathbf t_i ti?是multi-hot向量时,当 t i [ j ] = 1 , j ∈ { i 1 , i 2 , . . . , i k } \mathbf t_i[j] = 1,j \in \{i_1,i_2,...,i_k \} ti?[j]=1,j∈{i1?,i2?,...,ik?},则第 i i i个特征组的输入向量 t i \mathbf t_i ti?的低维稠密向量表示 { e i 1 , e i 2 , . . . , e i k } = { w i 1 i , w i ? 1 i , . . . , w i k i } \{\mathbf e_{i_1}, \mathbf e_{i_2}, ..., \mathbf e_{i_k} \} = \{ \mathbf w_{i_1}^i, \mathbf w_{i-1}^i, ..., \mathbf w_{i_k}^i \} {ei1??,ei2??,...,eik??}={wi1?i?,wi?1i?,...,wik?i?},是一组向量。
Pooling及Concat层
MLP输入向量时固定长度的,但是像用户历史行为特征,序列长度不一致,需要处理成一个固定长度的向量,因此需要对multi-hot的稠密向量进行处理。通过sum/average pooling方式对一组向量进行处理,得到特征组
i
i
i的最终低维稠密输入向量。
e
i
=
p
o
o
l
i
n
g
(
w
i
1
i
,
w
i
?
1
i
,
.
.
.
,
w
i
k
i
)
\mathbf e_i = pooling(\mathbf w_{i_1}^i, \mathbf w_{i-1}^i, ..., \mathbf w_{i_k}^i)
ei?=pooling(wi1?i?,wi?1i?,...,wik?i?)
然后所有的低维稠密输入向量进行拼接作为MLP的输入向量。
Loss
L
=
?
1
N
∑
(
x
,
y
)
∈
S
y
log
?
p
(
x
)
+
(
1
?
y
)
log
?
(
1
?
p
(
x
)
)
L=-\frac {1} {N} \sum_{(\mathbf x, y) \in S} y \log p(\mathbf x) + (1-y) \log (1-p(\mathbf x))
L=?N1?(x,y)∈S∑?ylogp(x)+(1?y)log(1?p(x))
p
(
x
)
p(\mathbf x)
p(x)是网络最后softmax后的输出,
y
∈
{
0
,
1
}
y \in \{0,1\}
y∈{0,1}表示label
DIN
base模型的缺陷:不论候选item是啥,用户的输入Embedding向量时一样的,没法表达用户的兴趣多样性。
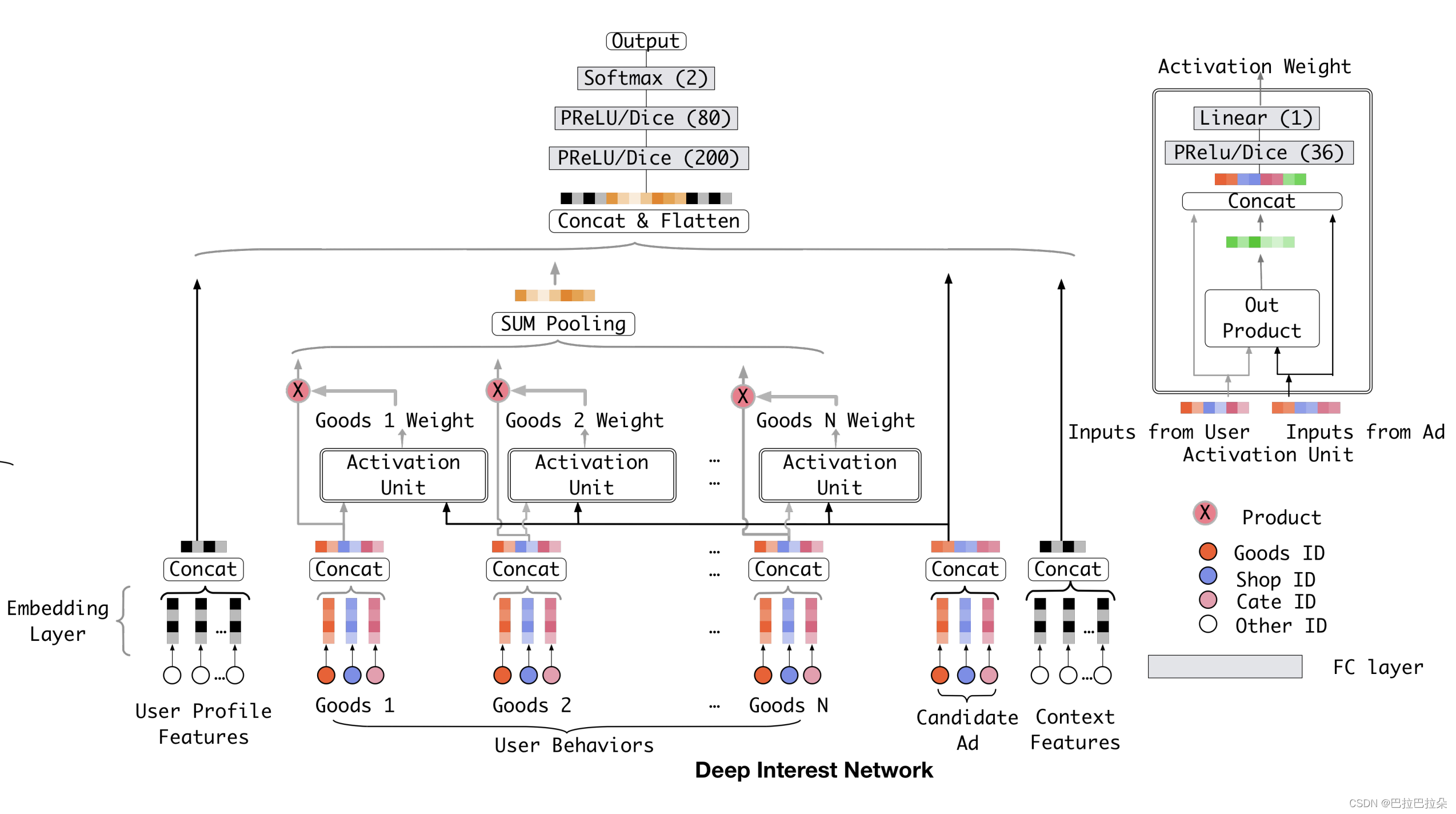
DIN引入了一个局部激活单元,其他结构一样。
局部激活单元
这个单元用在用户历史行为特征上面。和base模型的差别是将pooling操作改为Attention操作,将原先的多个历史行为Embedding的sum或者max操作改为按照与候选item的相关性对各个Embedding进行加权和操作。
假设候选item的Embedding输入向量是
v
A
\mathbf v_A
vA?,用户历史行为特征最后的结果向量
v
U
(
A
)
\mathbf v_U(A)
vU?(A)
v
U
(
A
)
=
f
(
v
A
,
e
1
,
e
2
,
.
.
.
,
e
H
)
=
∑
j
=
1
H
a
t
t
e
n
t
i
o
n
(
e
j
,
v
A
)
=
∑
j
=
1
H
w
j
e
j
\mathbf v_U(A) = f(\mathbf v_A,\mathbf e_1, \mathbf e_2, ..., \mathbf e_H ) = \sum_{j=1}^H attention(\mathbf e_j,\mathbf v_A) = \sum_{j=1}^H \mathbf w_j \mathbf e_j
vU?(A)=f(vA?,e1?,e2?,...,eH?)=j=1∑H?attention(ej?,vA?)=j=1∑H?wj?ej?
{ e 1 , e 2 , . . . , e H } \{\mathbf e_1, \mathbf e_2, ..., \mathbf e_H\} {e1?,e2?,...,eH?}是用户历史行为的一组Embedding,长度为 H H H
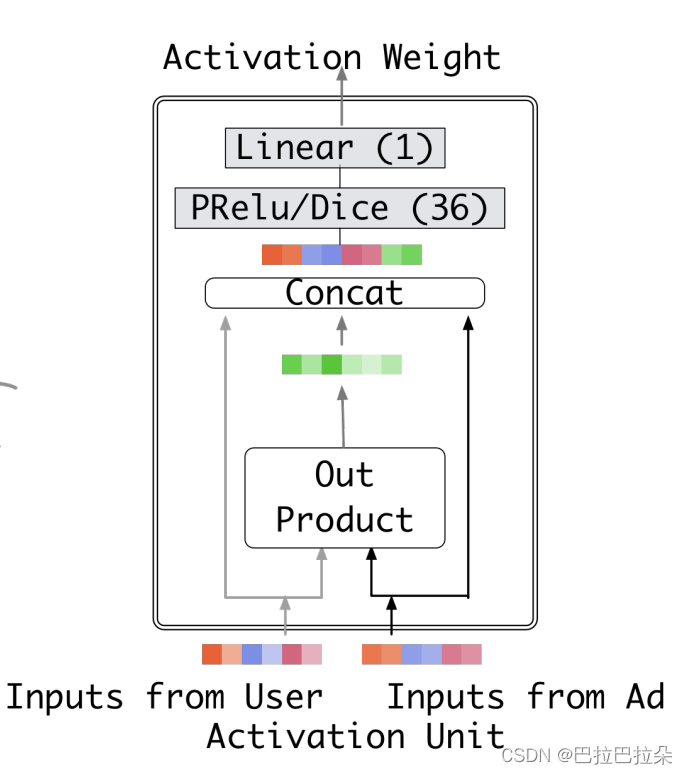
attention计算即局部激活单元,如下,用户向量和候选item向量计算out product(element-wise product),然后和用户向量、item向量拼接在一起,经过PRelu或者Dice激活函数,输入到一个单层网络,得到在给定item向量时用户向量的权重(相关性)结果。举例说明,如果用户历史序列有裙子,当候选是裙子时,裙子这个历史行为与当前候选item相关性高,计算得到的权重就大,那么最后用户历史行为特征Embedding结果中,裙子Embedding共享的就大(因为是各个历史行为的加权和
∑
j
=
1
H
w
j
e
j
\sum_{j=1}^H \mathbf w_j \mathbf e_j
∑j=1H?wj?ej?),其实就是Attention的核心思想。
Mini-batch Aware Regularization
提出原因:L2正则防止过拟合,但是每个batch里面都计算一次所有参数的正则,当参数量巨大时,会非常耗时。
通过仅计算batch内出现过的feature的正则,减少计算。Embedding词典
W
∈
R
D
×
K
\mathbf W \in R^{D \times K}
W∈RD×K参数最多,
W
\mathbf W
W的
l
2
l_2
l2?正则如下
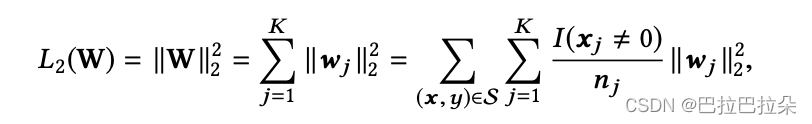
指示函数
I
(
x
j
≠
0
)
I(\mathbf x_j \neq 0)
I(xj??=0)表示输入样本
x
\mathbf x
x是否包含特征
j
j
j,
n
j
n_j
nj?表示特征
j
j
j在所有样本出现的次数。在batch中,正则如下
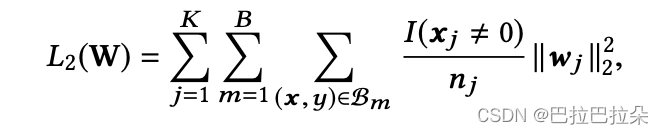
让
a
m
j
=
m
a
x
(
x
,
y
)
∈
B
m
I
(
x
j
)
a_{mj} = max_{(\mathbf x, y) \in B_m} I(\mathbf x_j)
amj?=max(x,y)∈Bm??I(xj?)表示batch
B
m
B_m
Bm?里面特征
j
j
j至少出现过一次
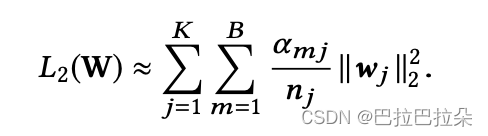
这样参数更新如下
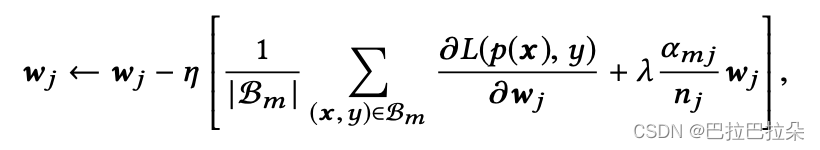
Dice激活函数
PReLU在值为0时有个突变点
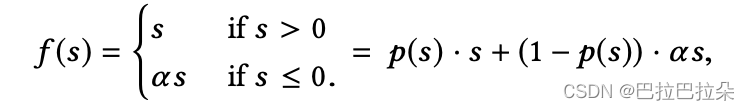
改为连续的,激活函数依赖于batch内数据的分布,
?
=
1
0
?
8
\epsilon = 10^{-8}
?=10?8是个常量,当均值和方差为0时,退化为PReLU。
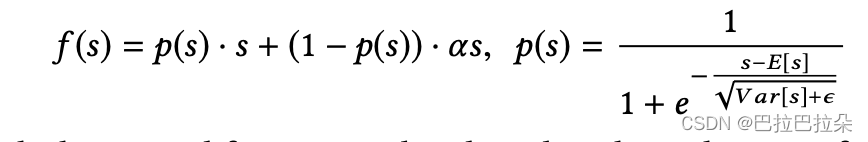
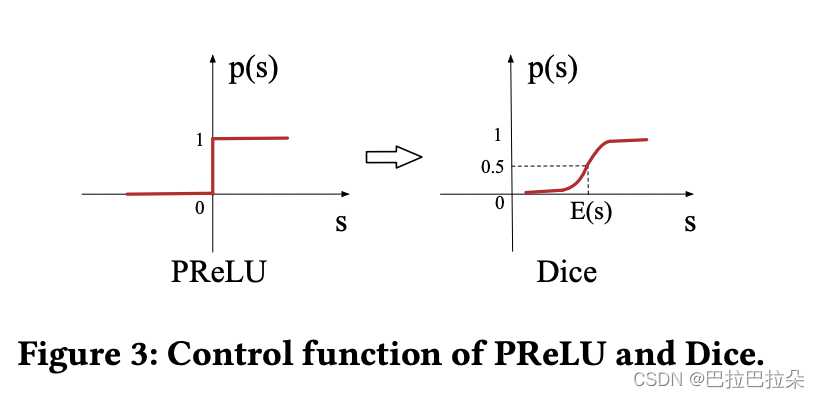
对比如下:
评估指标
使用GAUC,原因:GAUC能消除不同用户的差别,活跃用户和非活跃用户差别很大,使用曝光或者点击进行消除,按照曝光或者点击的权重进行加权。
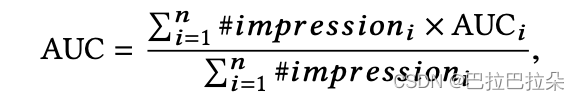
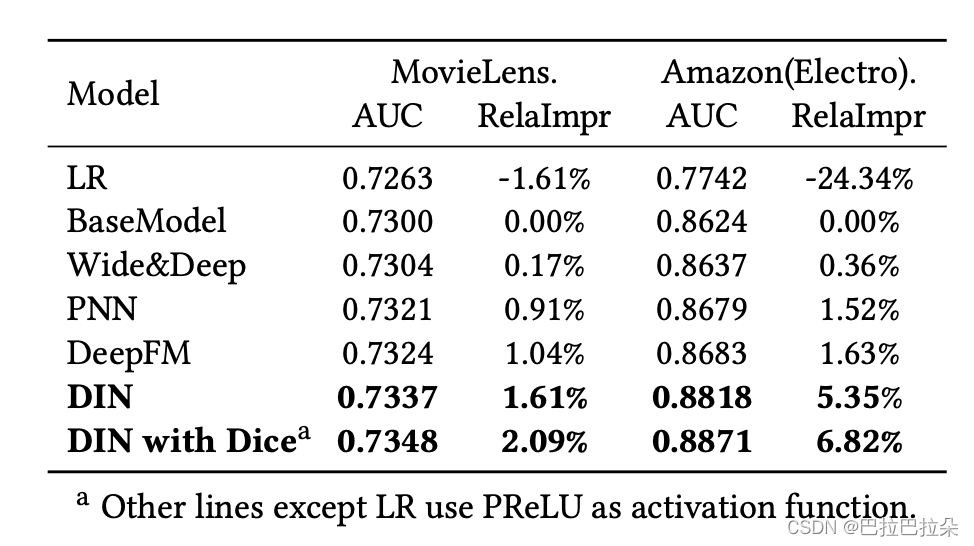
实验效果