一、噪音过滤
降维的目的之一是希望抛弃对模型带来负面影响的特征,同时,带有效信息的特征的方差应该是远大于噪音的,所以相比噪音,有效的特征所带来的信息不会在PCA当中大量抛弃。inverse_transform能够在不恢复原始数据的情况下,将降维后的数据返回到原本的高维空间。(即能够实现:“保证维度,但是去除方差很小的特征所带来的信息”)。我们可以利用·inverse_transform来实现噪音的过滤。
寻找确定关键特征是降噪的前提,只保留关键特征,其他都可以看做是噪音。
-
重要参数:n_components,svd_solver,random_state
-
三个重要属性:components_,explained_variance_以及explained_variance_ratio_
-
接口:fit,transform,fit_transform以及inverse_transform
1、案例:手写图像识别加噪与降噪
# 1. 导入所需要的库和模块
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
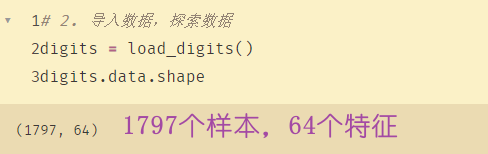
# 2. 导入数据,探索数据
digits = load_digits()
digits.data.shape
set(digits.target.tolist())

# 3. 定义画图函数
def plot_digits(data):
fig, axes = plt.subplots(4,10,figsize=(10,4)
,subplot_kw = {"xticks":[],"yticks":[]}
)
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8,8),cmap="binary")
plot_digits(digits.data)

# 4. 为数据加上噪音
np.random.RandomState(42)
noisy = np.random.normal(digits.data,2)
plot_digits(noisy)
为手写数据加上噪音之后的图片:

# 5. PCA降维
pca = PCA(0.5).fit(noisy) #改变参数
X_dr = pca.transform(noisy)
X_dr.shape

# 6. 逆转降维结果,实现降噪
without_noise = pca.inverse_transform(X_dr)
plot_digits(without_noise)
plt.show()
使用inverse_transform降噪后:

原来没有噪声的时候的维度:
without_noise.shape
2、案例:手写图像识别寻找最佳维度
# 1. 导入需要的模块和库
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# 2. 导入数据,探索数据
data = pd.read_csv(r"digit recognizor.csv")
X = data.iloc[:,1:]
y = data.iloc[:,0]
X.shape

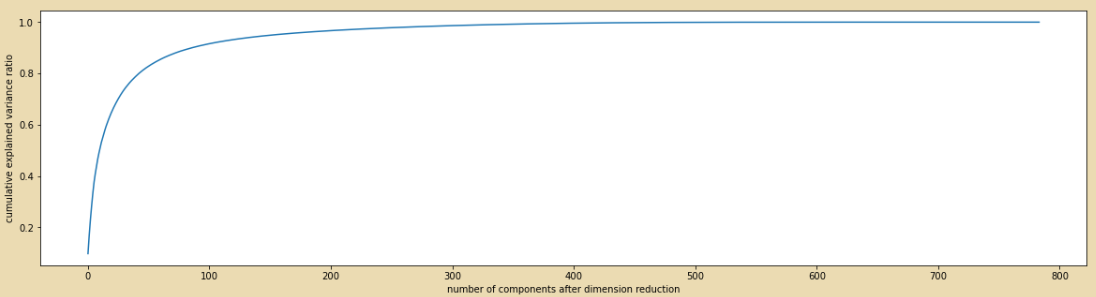
# 3. 画累计方差贡献率曲线,找最佳降维后维度的范围
pca_line = PCA().fit(X) #PCA,不填n_components,使用X.shape中的最小值
plt.figure(figsize=[20,5])
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))
plt.xlabel("number of components after dimension reduction") #降维后的特征书目
plt.ylabel("cumulative explained variance ratio") #累计可解释性方差累计曲线
plt.show() #0-200之间
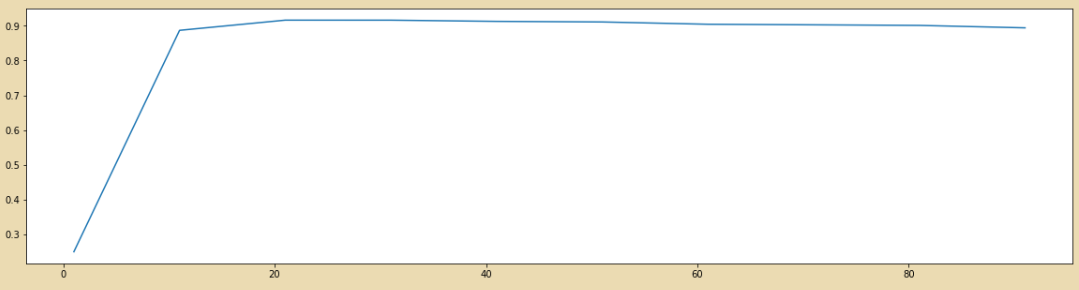
# 4. 降维后维度的学习曲线,继续缩小最佳维度的范围
score = []
for i in range(1,101,10): #取得0-100,用随机森林来跑
X_dr = PCA(i).fit_transform(X)
once = cross_val_score(RFC(n_estimators=10,random_state=0) #默认为10,保持稳定。
,X_dr,y,cv=5).mean() #5次交叉验证的值,取平均值
score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,101,10),score)
plt.show()
# 5. 细化学习曲线,找出降维后的最佳维度
score = []
for i in range(10,25): #再截取
X_dr = PCA(i).fit_transform(X)
once = cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()
score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10,25),score)
plt.show()
# 6. 导入找出的最佳维度进行降维,查看模型效果
X_dr = PCA(21).fit_transform(X) #取23、21
cross_val_score(RFC(n_estimators=100,random_state=0),X_dr,y,cv=5).mean()

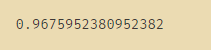
# 7. 更换模型
from sklearn.neighbors import KNeighborsClassifier as KNN
cross_val_score(KNN(),X_dr,y,cv=5).mean()
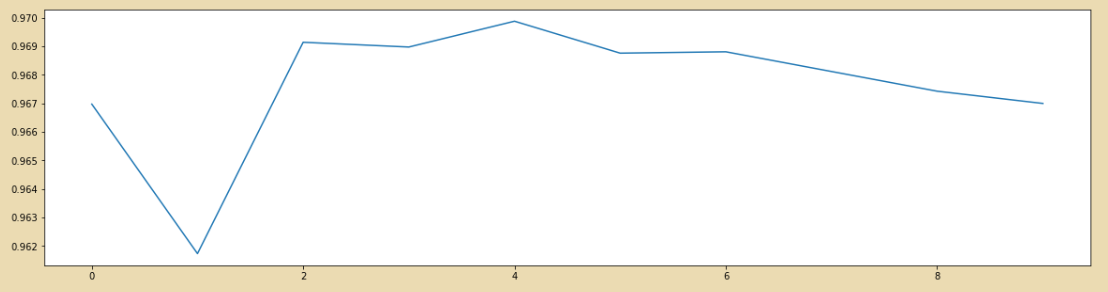
# 8. KNN的k值学习曲线
score = []
for i in range(10):
X_dr = PCA(23).fit_transform(X)
once = cross_val_score(KNN(i+1),X_dr,y,cv=5).mean()
score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10),score)
plt.show()
# 9. 定下超参数后,模型效果如何,模型运行时间如何?
cross_val_score(KNN(4),X_dr,y,cv=5).mean()

3、模拟PCA过程
##自适应求K值
import numpy as np
import cv2 as cv
# 数据中心化
def Z_centered(dataMat):
rows, cols = dataMat.shape
meanVal = np.mean(dataMat, axis=0) # 按列求均值,即求各个特征的均值
meanVal = np.tile(meanVal, (rows, 1))
newdata = dataMat - meanVal
return newdata, meanVal
# 最小化降维造成的损失,确定k
def Percentage2n(eigVals, percentage):
sortArray = np.sort(eigVals) # 升序
sortArray = sortArray[-1::-1] # 逆转,即降序
arraySum = sum(sortArray)
tmpSum = 0
num = 0
for i in sortArray:
tmpSum += i
num += 1
if tmpSum >= arraySum * percentage:
return num
# 得到最大的k个特征值和特征向量
def EigDV(covMat, p):
D, V = np.linalg.eig(covMat) # 得到特征值和特征向量
k = Percentage2n(D, p) # 确定k值
print("保留99%信息,降维后的特征个数:" + str(k) + "\n")
eigenvalue = np.argsort(D)
K_eigenValue = eigenvalue[-1:-(k + 1):-1]
K_eigenVector = V[:, K_eigenValue]
return K_eigenValue, K_eigenVector
# 得到降维后的数据
def getlowDataMat(DataMat, K_eigenVector):
return DataMat * K_eigenVector
# 重构数据
def Reconstruction(lowDataMat, K_eigenVector, meanVal):
reconDataMat = lowDataMat * K_eigenVector.T + meanVal
return reconDataMat
# PCA算法
def PCA(data, p):
dataMat = np.float32(np.mat(data))
# 数据中心化
dataMat, meanVal = Z_centered(dataMat)
# 计算协方差矩阵
# covMat = Cov(dataMat)
covMat = np.cov(dataMat, rowvar=0)
# 得到最大的k个特征值和特征向量
D, V = EigDV(covMat, p)
# 得到降维后的数据
lowDataMat = getlowDataMat(dataMat, V)
# 重构数据
reconDataMat = Reconstruction(lowDataMat, V, meanVal)
return reconDataMat
def main():
imagePath = '96014.jpg'
image = cv.imread(imagePath)
image = cv.cvtColor(image, cv.COLOR_BGR2GRAY)
rows, cols = image.shape
print("降维前的特征个数:" + str(cols) + "\n")
print(image)
print('----------------------------------------')
reconImage = PCA(image, 0.6) # 通过改变保留信息的程度来看这个图片的特征值
reconImage = reconImage.astype(np.uint8)
print(reconImage)
cv.imshow('test', reconImage)
cv.waitKey(0)
cv.destroyAllWindows()
if __name__ == '__main__':
main()
4、模拟SVD过程
def svd(img, topk_percent=0.1):
"""
使用svd对图片降维,可作为一种数据增强手段
每列作为一个向量,先构建方阵,再求特征值 特征向量,取前N个主成分,再重构图像
:param img: 输入图像
:param topk_percent: 图像恢复率,
:return: img after svd
"""
img_src = img[...] #img要三维的?
if len(img.shape) == 3:
img_src = cv2.cvtColor(img_src, cv2.COLOR_BGR2GRAY)
h, w = img_src.shape
data = np.asarray(img_src, np.double)
# 以下两种方式都可以
# method 1
U, s, V = np.linalg.svd(data)
K = round(len(s) * topk_percent)
S = np.diag(s)
major_data = np.dot(U[:, :K], np.dot(S[:K, :K], V[:K, :]))
# # method 2
# feat_values, feat_vectors = np.linalg.eig(np.dot(data.T, data))
# feat_index = np.argsort(np.sqrt(feat_values), axis=0)[::-1]
# S = np.diag(feat_values)
# V = feat_vectors[:, feat_index]
# S_inv = np.asmatrix(S).I
# V_inv = np.asmatrix(V).I
# U = np.dot(np.dot(data, V), S_inv)
# K = round(S.shape[0] * topk_percent)
# major_data = np.dot(np.dot(U[:, :K], S[:K, :K]), V_inv[:K, :])
rebuild_img = np.asarray(major_data, np.uint8)
cv2.imshow('1', rebuild_img)
cv2.waitKey(0)
return rebuild_img
def pca(img, topk_percent=0.1):
"""
使用pca对图片降维,可作为一种数据增强手段
每列作为一个向量,先0均值化,再求协方差矩阵的特征值和特征向量,取前N个主成分,再重构图像
:param img: 输入图像
:param topk_percent: 图像恢复率,
:return: img after pca
"""
img_src = img[...]
if len(img.shape) == 3:
img_src = cv2.cvtColor(img_src, cv2.COLOR_BGR2GRAY)
print(img_src.shape)
h, w = img_src.shape
data = np.asarray(img_src, np.double)
# 计算每列的mean
_mean = np.mean(data, axis=0)
data -= _mean
# 以 列为变量计算方式,计算协方差矩阵
data_cov = np.cov(data, rowvar=False)
feat_values, feat_vectors = np.linalg.eig(data_cov)
feat_index = np.argsort(np.sqrt(feat_values), axis=0)[::-1]
V = feat_vectors[:, feat_index]
K = round(len(feat_values) * topk_percent)# 重建图像
major_data = np.dot(np.dot(data, V[:, :K]), V[:, :K].T) + _mean
rebuild_img = np.asarray(major_data, np.uint8)
cv2.imshow('0', rebuild_img) #参数错误1应该为0
cv2.waitKey(0)
return rebuild_img
