文章目录
惯性导航算法
前言:对于姿态、速度和位置的解算,我们一般都是先推出连续时间的微分方程,然后对其进行数值求解,然后得到一个离散化的,可用计算机执行的,更新算法
惯导机械编排算法
预备知识
惯性导航中的常用坐标系
地心惯性坐标系(i),地心地固坐标系(e),导航坐标系(n),载体坐标系(b)
地球表面导航的主要状态量
位置:地心->载体
速度:地速
姿态:b系相对于n系(或e系)
导航状态量的表示
位置、速度、加速度和角速度等状态量用向量来表示,准确的
表达涉及三种坐标系

1.要注意,不能混淆向量与向量的坐标,向量的坐标只是向量的一种表示/描述;而向量是唯一的。
2.姿态不能用向量表示
位置向量

速度向量

姿态
欧拉角
方向余弦矩阵
四元数
旋转矢量(描述姿态变化)
角速度向量
任意坐标系b 相对于参考坐标系R 的转动角速度向量,在坐标
系p 下的投影,可写成如下向量符号

反对称矩阵
反对称矩阵是向量的另一种表达形式

IMU 的增量输出
实际的中高精度的惯导,输出的不是陀螺输出角速度和加速度计输出比力,而是陀螺输出角增量,加速度计输出速度增量,是一个短时间内的积分
速度增量和角度增量输出
采样定理: 带宽vs. 数据率(香农采样定律,也就是采样率fs要大于被测信号带宽的2倍2*BW,否则就不能用离散化的采样来恢复原来的信号;这样就能在把连续时间变化的信号离散化的过程中的损失降到最小)
连续时间vs. 离散时间
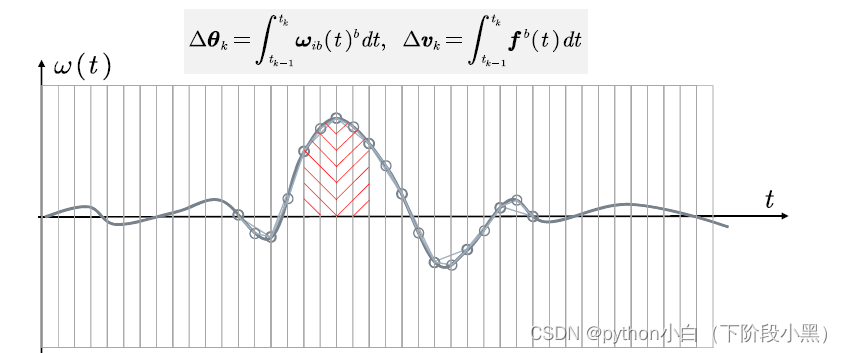
上图(纵轴为角速度)表示,采样率增大(加密)就可以降低在离散化中的精度损失,因此必须要极高采样率,但是这样会极大的增加工作量(而且对硬件和功耗要求也很高);因此,前辈们就想到了,在采集的时候,就先把那一段时间的角增量,也就是那一小块的面积计算出来(把积分的过程提前),然后后面处理的时候直接相加,就能得到姿态,因此,惯导的输出一般都采用增量的形式
圆锥效应(对应姿态计算补偿), 划桨效应(对应速度计算补偿),涡卷效应(对应位置计算补偿)
上面三个效应补偿,可以应对,由于离散化,造成的三维解算的损失

有些厂家,在实际应用时,用到的确实是增量,但是为了输出数据信息的直观性,就将增量除以了时间t,表示成了平均角速度和平均比力,这个需要注意。本质上仍然是增量。
惯导机械编排原理
捷联惯导利用陀螺的原始测量值计算载体姿态矩阵,通
过姿态矩阵把加速度计测量的载体的沿载体坐标系轴向
的比力信息转换到特定的坐标系中(如导航坐标系),
然后进行导航解算。
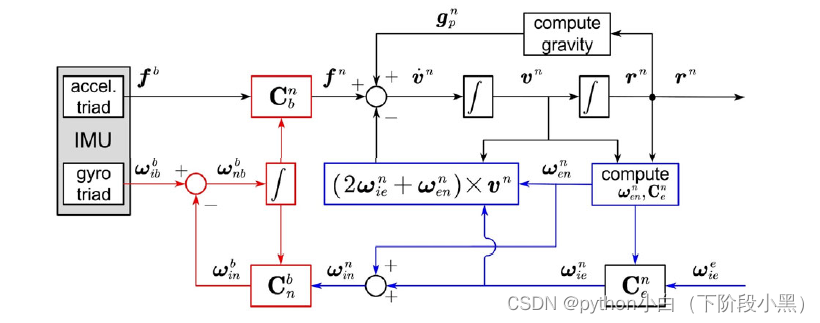
惯性导航姿态算法
欧拉角
姿态及其作用
1.姿态(attitude)描述的是一个坐标系的轴系相对于另一
个坐标系的轴系之间的角度关系(方向)
2.坐标系可以看成刚体,而姿态是描述刚体的六参数(三
个坐标和三个轴向角度)中的三个。描述姿态需要三个
独立参数
3.在惯性导航中,姿态主要用于比力、角速度及其它向量
的投影变换(例如从载体坐标系变换到导航坐标系)
欧拉角
欧拉证明任意两个正交坐标系之间的相对朝向关系可以通过一组不少于3的角度来描述。这三次旋转的转角称为一组欧拉角,因最早由欧拉(Leonhard Euler )提出而得名。
注:三个姿态角就是一组欧拉角
欧拉旋转定理
在运动学里,欧拉旋转定理表明,在三维空间里,假设一个刚体在做一个旋转的时候,刚体内部至少有一点固定不动,则此位移等价于一个绕着包含那固定点的固定轴(这个固定轴所在的矢量,就是等效旋转矢量)的旋转。
注:等效旋转矢量就是基于欧拉旋转定理提出的
欧拉角组
1.在三维欧氏空间里,任何两个正交坐标系都可以用坐标变换
把它们联系起来,而坐标变换又可以用坐标旋转来得到。
2.一个动坐标系相对参考坐标系的方位,可以完全由动坐标系
依次绕三个不同的转轴的转角来确定。
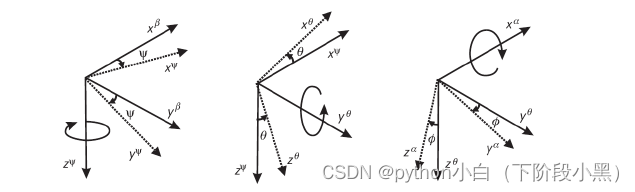
3.在给定一组欧拉角表示两个坐标系间的姿态关系时,一定要同时指定对应的转轴顺序才有意义。
常用姿态角的定义

