[人工智能] 2022.05.17

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 2022.05.17 - 2022.05.22 -> 正文阅读

[人工智能]2022.05.17 - 2022.05.22

2022-05-17

防御对抗攻击：Gotta Catch ’Em All: Using Honeypots to Catch Adversarial Attacks on Neural Networks (CCS '20: Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications SecurityOctober 2020)
论文背景
??深度神经网络 (DNN) 容易受到对抗性攻击(主要的攻击方法：FGSM，PGD，CW，Elastic Net，BPDA，SPSA 暂时没有深入调研攻击方式，后面会陆续给出几种攻击方式的原理)，只要提供经过训练的模型，就可以修改输入从而产生错误输出。这些修改后的对抗样本能有效欺骗在不同训练数据不同子集上的训练模型。事实证明，对抗性攻击对部署在现实环境中的模型有效，例如无人驾驶汽车、面部识别和物体识别系统。针对对抗性攻击已有的防御方法主要有两种 “对抗训练(Adversarial training)” 和 “梯度掩蔽(Gradient masking)” 。
??对抗训练：在对抗性训练中，防御者通过将对抗性示例合并到训练数据集中来为模型接种疫苗以抵御给定的攻击。这种 “对抗性” 训练过程降低了模型对特定已知攻击的敏感性。
??梯度掩蔽：防御者训练一个具有小梯度的模型，使得模型对输入空间上小的变化具有鲁棒性(例如对抗性干扰)，“防御性蒸馏” 就是该方法的一个例子，首先正常训练得到模型一 $\mathcal{F}_\theta$ ，然后使用 $\mathcal{F}_\theta$ 输出的分类概率作为输入训练得到模型二 $\mathcal{F}^\prime_\theta$ , 用 $\mathcal{F}^\prime_\theta$ 替代 $\mathcal{F}_\theta$ 达到梯度掩蔽的目的。
??但是 (1) “对抗训练” 可以使用新的攻击或对已知攻击的不同参数来攻破。(2) “梯度掩蔽" 可以从对抗样本的生成上小的调整可以克服这种防御。
整体框架
图一是
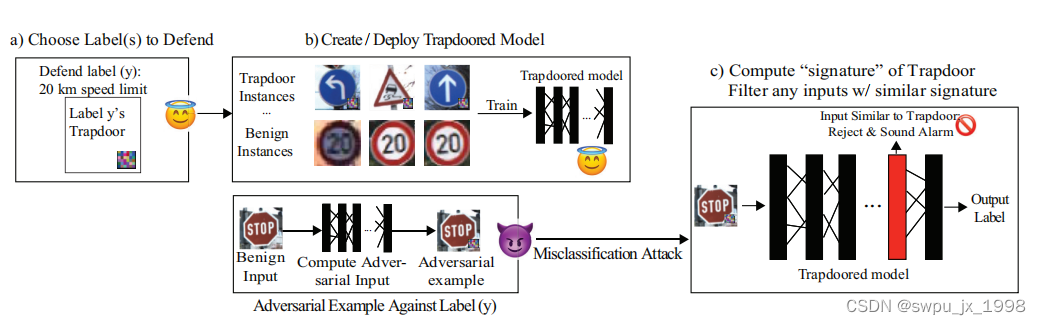
作者提出了一种新的 “陷门防御(trapdoor defense)”
a) 选择需要防御的目标标签。b) 为每个目标标签创建不同的陷门并将它们嵌入到模型中。为每个嵌入式陷门部署模型并计算激活签名。 c) 可以访问模型的对手构建了一个对抗样本。在运行时，模型将每个输入的神经元激活特征与陷门的特征进行比较。因此，它识别出攻击并发出警报。

2022-05-18

Fast Gradient Sign Method(FGSM)方法

??作者Goodfellow 在其对对抗样本的线性解释的理论下提出了该方法。首先来看作者提出的对抗样本的线性解释
??因为样本输入特征(input feature)的精度有限(一般图像的每个像素是8bits, 样本中所有低于1/255的信息都会被丢弃)，所以当样本 $x$ 中每个元素值添加的扰动值 $\eta$ 小于样本输入特征精度时，分类器无法将样本 $x$ 和对抗样本 $\hat{x}=x + \eta$ 区分开。对于分类器而言，如果 $\epsilon$ 是一个足够小以至于被舍弃掉的值，那么只要 $\|\eta\|_\infin < \epsilon$ ，分类器将认为 $x$ 和 $\hat{x}$ 属于同一个类。然后考虑权重向量 $\omega^T$ 和对抗样本 $\hat{x}$ 的点积 $\omega^T\hat{x} = \omega^T(x + \eta) = \omega^Tx + \omega^T\eta$ 。那么扰动使得结果增加了 $\omega^T\eta$ ，作者为了最大化 $\omega^T\eta$ , 让 $\eta=sign(\omega)$ 。假设权重向量 $\omega$ 有 $n$ 个维度，且权重向量中元素的平均量值是 $m$ ，那么结果将增加 $\epsilon mn(\Rightarrow \omega^T\eta \le nm\epsilon)$ 。虽然 $\|\eta\|_\infin$ 不会随着维度 $n$ 的变化而变化，但是由 $\eta$ 导致的增量 $\epsilon mn$ 会随着维度 $n$ 线性增长。那么对于一个高维度的问题，一个样本中大量维度的无限小的干扰加在一起就可以对输出造成很大的变化。所以对抗样本的线性解释表明，对线性模型而言，如果其输入样本有足够大的维度，那么线性模型也容易受到对抗样本的攻击。
??作者利用对抗样本的线性解释提出了一个快速产生对抗样本的方式，也即 Fast Gradient Sign Method(FGSM) 方法。假设模型的参数值为 $\theta$ ，模型的输入是 $x$ ， $y$ 是模型对应的label值， $J(\theta,x,y)$ 是训练神经网络的损失函数。对某个特定的模型参数 $\theta$ 而言，FGSM方法将损失函数近似线性化，从而获得保证无穷范数限制的最优的扰动(即 $\|\eta\|_\infin < \epsilon$ )，扰动值具体为：
$\eta = \epsilon sign(\nabla_xJ(\theta,x,y))$
代码实现：在tensorflow的预训练模型实现对抗攻击

import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np

mpl.rcParams['figure.figsize'] = (8, 8)
mpl.rcParams['axes.grid'] = False

#让我们加载预训练的 MobileNetV2 模型和 ImageNet 类名。

pretrained_model = tf.keras.applications.MobileNetV2(include_top=True,
                                                     weights='imagenet')
pretrained_model.trainable = False

# ImageNet 的标签对象
decode_predictions = tf.keras.applications.mobilenet_v2.decode_predictions

# 将图像转化为 MobileNetV2 的输入格式
def preprocess(image):
  image = tf.cast(image, tf.float32)
  image = tf.image.resize(image, (224, 224))
  image = tf.keras.applications.mobilenet_v2.preprocess_input(image)
  image = image[None, ...]
  return image

# 根据预测结果提取图形标签
def get_imagenet_label(probs):
  return decode_predictions(probs, top=1)[0][0]


image_path = tf.keras.utils.get_file('YellowLabradorLooking_new.jpg', 'https://storage.googleapis.com/download.tensorflow.org/example_images/YellowLabradorLooking_new.jpg')
image_raw = tf.io.read_file(image_path)
image = tf.image.decode_image(image_raw)

image = preprocess(image)
image_probs = pretrained_model.predict(image)

plt.figure()
plt.imshow(image[0] * 0.5 + 0.5)  # To change [-1, 1] to [0,1]
_, image_class, class_confidence = get_imagenet_label(image_probs)
plt.title('{} : {:.2f}% Confidence'.format(image_class, class_confidence*100))
plt.show()

# 实现快速梯度符号法
# 第一步是创建扰动，用于扭曲原始图像，从而产生对抗性图像。如前所述，对于此任务，梯度是相对于图像进行的。
loss_object = tf.keras.losses.CategoricalCrossentropy()

def create_adversarial_pattern(input_image, input_label):
  with tf.GradientTape() as tape:
    tape.watch(input_image)
    prediction = pretrained_model(input_image)
    loss = loss_object(input_label, prediction)

  # Get the gradients of the loss w.r.t to the input image.
  gradient = tape.gradient(loss, input_image)
  # Get the sign of the gradients to create the perturbation
  signed_grad = tf.sign(gradient)
  return signed_grad

# 获取输入图片的标签的one-hot编码
labrador_retriever_index = np.argmax(image_probs)
label = tf.one_hot(labrador_retriever_index, image_probs.shape[-1])
label = tf.reshape(label, (1, image_probs.shape[-1]))

perturbations = create_adversarial_pattern(image, label)
plt.imshow(perturbations[0] * 0.5 + 0.5);  # To change [-1, 1] to [0,1]
plt.show()

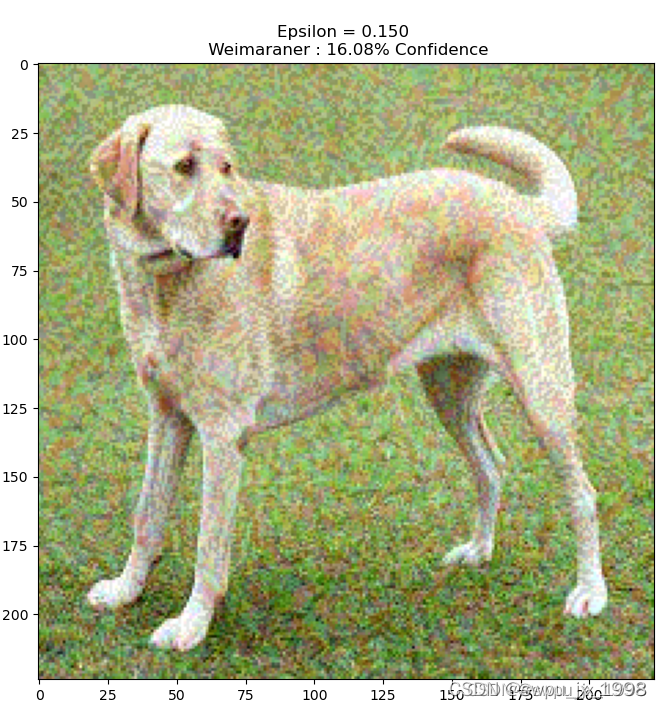
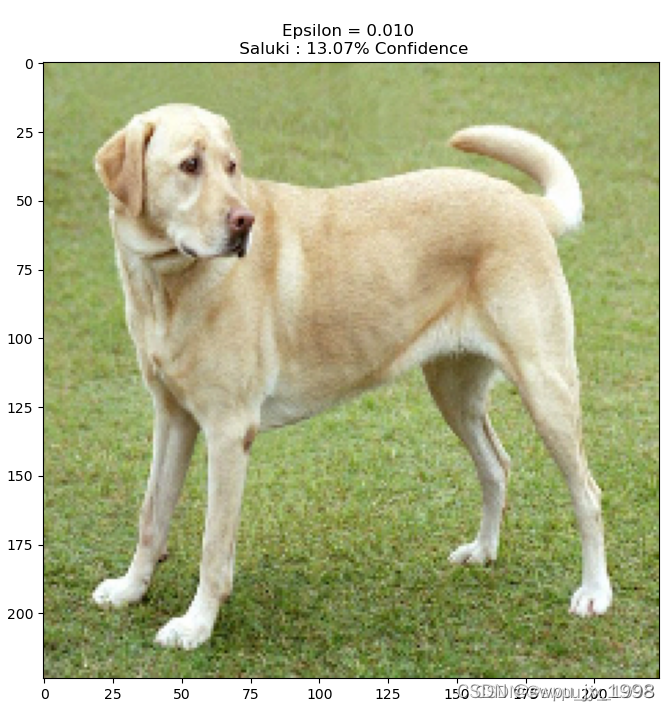
# 让我们尝试不同的 epsilon 值并观察生成的图像。您会注意到，随着 epsilon 值的增加，欺骗网络变得更加容易。然而，这是一种权衡，导致扰动变得更加可识别。
def display_images(image, description):
  _, label, confidence = get_imagenet_label(pretrained_model.predict(image))
  plt.figure()
  plt.imshow(image[0]*0.5+0.5)
  plt.title('{} \n {} : {:.2f}% Confidence'.format(description,
                                                   label, confidence*100))
  plt.show()

epsilons = [0, 0.01, 0.1, 0.15]
descriptions = [('Epsilon = {:0.3f}'.format(eps) if eps else 'Input')
                for eps in epsilons]

for i, eps in enumerate(epsilons):
  adv_x = image + eps*perturbations
  adv_x = tf.clip_by_value(adv_x, -1, 1)
  display_images(adv_x, descriptions[i])

2022-05-19

Projected Gradient Descent (PGD/BIM)方法

??BIM 是Goodfellow和Kurakin等人对FGSM的扩展。一般有FGSM生成的对抗样本成功率与步长 $\epsilon$ 密切相关， $\epsilon$ 太大，整体图形效果不好， $\epsilon$ 太小，又无法实现对抗攻击，于是，他们通过每一次迭代仅生成很小的扰动，经过多次迭代得到最后的结果，以此来拓展FGSM。定义如下
$\rm{Clip}_{x,\epsilon} \{x^\prime\} = \rm{min}\{255, x+\epsilon, \rm{max}\{0, x-\epsilon,x^\prime\}\},$
其中 $\rm{Clip}_{x,\epsilon} \{x^\prime\}$ 限制了生成的对抗样本扰动在图像的正常像素范围之类。采用下面的迭代步骤：

$x_0 = x\\ \vdots \\ x^\prime_{n+1} = \rm{Clip}_{x,\epsilon}\{x_n + \alpha\rm{sign}\it{(\nabla_xJ(\theta,x,y))}\},$
式子中的 $\alpha=1$ 则表示每一次迭代对每个像素的值更改了1
??FGSM等同于迭代一次的BIM，上述方法通过增加损失函数值的大小，迫使标签变化，没有明确指定往哪个标签偏移，主要是针对非目标攻击。

代码实现：使用pytorch训练一个手写字母识别模型（这部分代码省略）然后生成对抗样本

#adv_examples:需要生成对抗样本的目标样本；adv_target: 目标原始标签
#epochs表示迭代的次数，即公式中的 n；model:训练好的手写字母识别模型
def train_adv_bim(
        model: nn.Module, loss_fct: callable, adv_examples: torch.Tensor, adv_targets: torch.Tensor,
        epochs: int = 10, alpha: float = 1.0, clip_eps: float = (1 / 255) * 8
):
    return train_adv_examples(
        model, loss_fct, adv_examples, adv_targets,
        epochs=epochs, alpha=alpha, do_clip=True, clip_eps=clip_eps, minimize=False
    )


def train_adv_examples(
        model: nn.Module, loss_fct: callable, adv_examples: torch.Tensor, adv_targets: torch.Tensor,
        epochs: int = 10, alpha: float = 1.0, clip_eps: float = (1 / 255) * 8, do_clip: bool = False, minimize: bool = False
):
    model.eval()
    for e in range(epochs):
        adv_examples.requires_grad = True
        model.zero_grad()

        adv_out = model(adv_examples)
        loss = loss_fct(adv_out, adv_targets)
        loss.backward()

        adv_grad = adv_examples.grad
        adv_examples = adv_examples.detach()

        adv_sign_grad = adv_examples + alpha * adv_grad.sign()
        adv_examples = clip(adv_examples, adv_sign_grad, clip_eps)
    return adv_examples

def clip(x, x_, eps):
    mask = torch.ones_like(x)
    lower_clip = torch.max(torch.stack([mask * 0, x - eps, x_]), dim=0)[0]
    return torch.min(torch.stack([mask, x + eps, lower_clip]), dim=0)[0]

混淆矩阵：左图为原始图，右图为对应的对抗样本

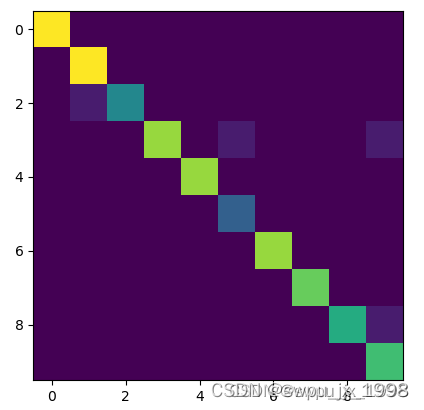
原始图与对抗样本的对比：左图为原始图，右图为对抗样本

?? ?? ?? ?? ?? ??Carlini and Wagner Attack (CW) 方法

…

Elastic Net 方法

…

Backward Pass Differentiable Approximation (BPDA) 方法

…

Simultaneous Perturbation Stochastic Approximation (SPSA) 方法

…

2022-05-20

??理论上来说，trapdoor 是为特定的标签 $y_t$ 设计的特有的扰动，用 $\Delta$ 表示，这样模型会把任何包含 $\Delta$ 的输入 $x$ 都分类为 $y_t$ , 也就是说 $\mathcal{F}_{\theta}(x + \Delta) = y_t, \forall x$ 。对于攻击者来说，如果其目标是 $y_t$ , 那么就需要找到一个扰动 $\epsilon$ 使得 $\mathcal{F}_{\theta}(x + \epsilon) = y_t\not=\mathcal{F}_{\theta}(x)$ , 进一步说，就是使得优化函数的损失最小，即 $\rm{min} \it{J(y_t,\mathcal{F}_\theta(x+\epsilon))}$ 。如果一个模型已经注入了 $\Delta$ , 那么攻击者的优化函数会收敛到靠近 trapdoor 的损失函数的邻域内。下图是一个正常模型和trapdoored模型的损失函数的假设图，trapdoor 在A和B之间创造了一个大的局部最小值，攻击者的损失函数会收敛到这个局部最小值（这一部分的理论证明会在后面给出，下面先来看看具体的做法）

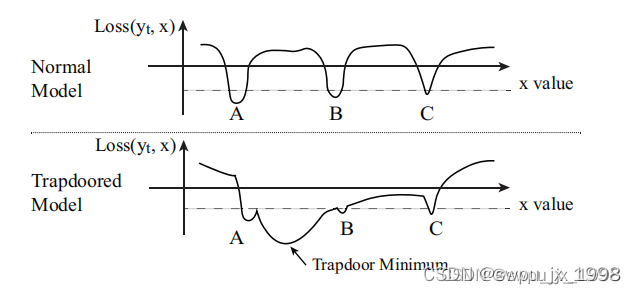
Defending a Single Label

Step 1: Embedding Trapdoors

??首先通过将陷门扰动注入随机选择的正常输入并将它们与标签 $y_t$ 关联而生成的新实例来扩充原始训练数据集，从而创建陷门训练数据集。新实例定义如下
$x^\prime = x + \Delta := \mathcal{I}(x, \it{M}, \it{\delta}, k),$
其中 $x^{\prime}_{i,j,c} = (1-m_{i,j,c}) \cdot x_{i,j,c} + m_{i,j,c}\cdot \delta_{i,j,c}$ , 这里 $\mathcal{I}(\cdot)$ 是注入函数， $\Delta = (M,\delta,k)$ 是 $y_t$ 的扰动。 $\delta, M$ 和 $x$ 具有相同的形状， $\delta$ 是扰动模式，是一个随机值矩阵。 $M$ 是 $\; mask$ ，指定了扰动应该覆盖原始图像的程度， $M$ 中的每一个元素 $m_{i,j,c} \in [0,1]$ 。文中设置 $m_{i,j,c} \in \{0, k\}$ , $k < < 1$ 。 $k$ 称为 $\; ratio$ (覆盖比例) 。

Step 2: Training the Trapdoored Model

??trapdoor model的目标是对于干净的图片能达到很高的准确率，同时把任何包含 $\Delta=(M,\delta,k)$ 的图片分类为 $y_t$ 。这一优化目标和向神经网络注入一个后门的过程很相似。
$\underset{\theta}{\rm{min}}\; J(y,\mathcal{F}_{\theta}(x)) + \lambda\cdot J(y_t, \mathcal{F}_{\theta}(x+\Delta)) \\ \forall x \in \mathcal{X} \; \rm{where} \; \it{y} \not= y_t,$
其中 $y$ 是 $x$ 的真实标签。训练好一个trapdoor model 后，定义 $\Delta$ 的 $“trapdoor\; signature”$ 表示如下
$\mathcal{S}_{\Delta} = \mathbf{E}_{x\in \mathcal{X},y_t \not=\mathcal{F}_{\theta}(x)}g(x + \Delta),$
其中 $\mathbf{E}(\cdot)$ 表示期望， $g(\cdot)$ 是模型对输入 $x$ 的特征表示，文中作者应用的是模型的最后一层 softmax 层的输入。 $\mathcal{S}_{\Delta}$ 的定义分析在后面会给出。下图简单的描述了 $\mathcal{S}_{\Delta}$ 的计算过程。

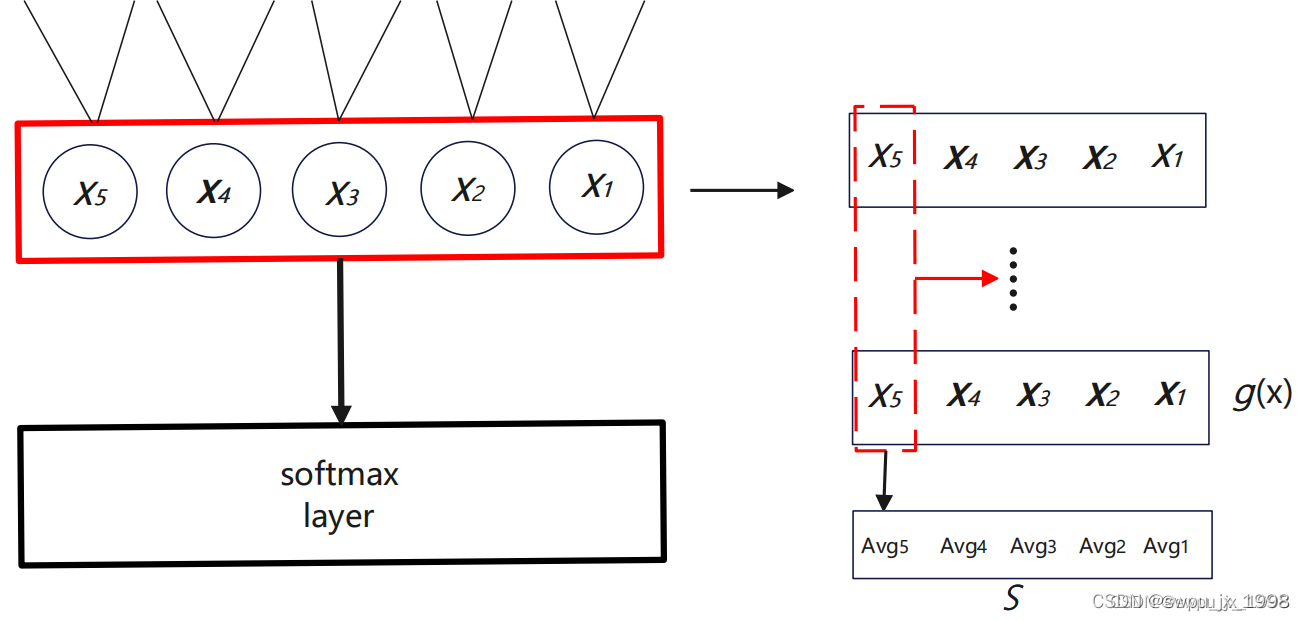
Step 3: Detecting Adversarial Attacks

??对于目标 $y_t$ 的对抗样本 $x+\epsilon$ 输入到训练好的trapdoor model，可以得到 $\epsilon)$ ，通过比较 $\epsilon)$ 和 $\mathcal{S}_{\Delta}$ 的相似程度来检测对抗样本。文中使用 cosine 相似度来衡量二者之间的相似性，即 $cos(g(x+\epsilon),\mathcal{S}_{\Delta})$ 。如果相似度超过一个预设的阈值 $\phi_t$ ，那么就认为是对抗样本。文中通过计算已知良性图像和陷门图像之间相似度的统计分布来配置 $\phi_t$ 。 $\; choose \; \phi_t\; to \; be \; the \; k^{th}\; percentile \; value \; of \; this \; distribution, \; where \; 1-\frac{k}{100}\; is \; the \; desired \; false \; positive \; rate \;"$ (关于 $\phi_t$ 的设置暂时还没看懂，需要结合代码来理解)。

Defending Multiple Labels

??通过单个标签的防御可以扩展到多标签的防御。另 $\Delta_t = (M_t,\delta_t,k_t)$ 代表标签 $y_t$ 。相应的用于训练保护所有标签的陷阱模型的优化函数定义为
$\underset{\theta}{\rm{min}}\; J(y,\mathcal{F}_{\theta}(x)) + \lambda\cdot \sum_{ y_t\in \mathcal{Y}, y_t\not=y}J(y_t,\mathcal{F}_{\theta}(x + \Delta_t))$