[人工智能]机器学习问题汇总（回归+聚类）

回归

1. L1和L2正则化的区别

正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或惩罚项。正则化项是模型复杂度的单调递减函数，模型越复杂，正则化值就越大。

正则化一般具有如下形式：
$min\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)$
其中，第1项是经验风险，第2项是正则化项，$\lambda \ge 0$为调整两者之间关系的系数。

$L_1$正则化可以是参数向量的$L_1$范数：
$L(\omega )=\frac{1}{N}{\sum }_{i=1}^N(f(x_i;\omega )?y_i{)}^2+\lambda \Vert \omega {\Vert }_1$

$L_2$正则化可以是参数向量的$L_2$范数：
$L(\omega )=\frac{1}{N}{\sum }_{i=1}^N(f(x_i;\omega )?y_i{)}^2+\frac{\lambda }{2}\Vert \omega {\Vert }^2$

用$L_1$损失函数的好处：
鲁棒性更强，对异常值更不敏感。
用$L_2$损失函数的好处：
计算方便，可以直接求导获得取最小值时各个参数的取值。

2. Loss Function有哪些，怎么用？

统计学习常用的损失函数有以下几种：
1）0-1损失函数

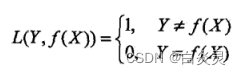
2）平方损失函数
$L(Y,f(X))=(Y?f(X){)}^2$

3）绝对损失函数
$L(Y,f(X))=|Y?f(X)|$

4）对数损失函数或对数似然损失函数
$L(Y,P(Y|X))=?logP(Y|X)$

3. 线性回归的表达式

线性模型用向量形式写成$f(x)={\omega }^{T}x+b$

4. 线性回归的损失函数

损失函数：
$$\begin{gathered} ({\omega }^{?},b^{?})=ar{g}_{(w,b)}min{\sum }_{i=1}^m(f(x_i)?y_i{)}^2 \\ =ar{g}_{(w,b)}min{\sum }_{i=1}^m(y_i?\omega x_i?b{)}^2 \end{gathered}$$

5. 哪些传统的回归机器学习模型

线性回归、岭回归、套索回归

聚类

1. DBSCAN原理

几个概念的定义：
1）$??$邻域：对$x_j\in D$，其$??$邻域包含样本集$D$中与$x_j$的距离不大于$?$的样本，即$N_{?}(x_j)=x_j\in D|dist(x_i,x_j)\le ?$
2）核心对象：若$x_j$的$??$邻域至少包含$MinPts$个样本，即$|N_{?}(x_j)|\ge MinPts$，则$x_j$是一个核心对象
3）密度直达：若$x_j$位于$x_i$的$??$邻域中，且$x_i$是核心对象，则成$x_j$由$x_i$密度直达
4）密度可达：对$x_i$与$x_j$，若存在样本序列$p_1,p_2,...,p_n$，其中$p_1=x_i,p_n=x_j$且$p_{i+1}$由$p_i$密度直达，则称$x_j$由$x_i$密度可达
5）密度相连：对$x_i$与$x_j$，若存在$x_k$使得$x_i$与$x_j$均由$x_k$密度可达，则称$x_i$与$x_j$密度相连。

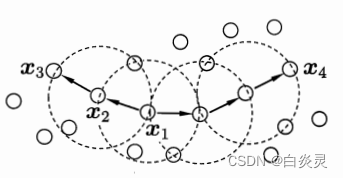
这里，$MinPts=3$，虚线显示出$??$邻域，$x_1$是核心对象，$x_2$由$x_1$密度直达，$x_3$由$x_1$密度可达，$x_3$与$x_4$密度相连。

1）DBSCAN通过检查数据集中每点的$??$来搜索簇，如果点p的$??$邻域包含的点多于$MinPts$个，则创建一个以p为核心对象的簇。
2）然后，DBSCAN迭代地聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并。
3）当没有新的点添加到任何簇时，该过程结束。

2. DBSCAN算法伪代码

3. DBSCAN的优缺点

优点：
基于密度定义，相对抗噪声，能处理任意形状和大小的簇
缺点：
1）当簇的密度变化太大时，会有麻烦
2）对于高维问题，密度定义是个比较麻烦的问题

4. k-means算法流程

5. KMeans原理

给定样本集 D = { x 1 , x 2 , . . . , x m } D=\{x_1,x_2,...,x_m\} D={x1?,x2?,...,xm?}，“k-均值”算法针对聚类所得簇划分 C = { C 1 , C 2 , . . . , C k } C=\{C_1,C_2,...,C_k\} C={C1?,C2?,...,Ck?}最小化平方误差：
$E={\sum }_{i=1}^k{\sum }_{x\in C_i}\Vert x?{\mu }_i{\Vert }_2^2$

其中${\mu }_i=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$是簇$C_i$的均值向量。

上式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，$E$值越小则簇内样本相似度越高。

6. KMeans的K怎么确定

1）肘部法
肘部法所使用的聚类评价指标：
数据集中所有样本点到其簇中心的距离之和的平方，肘部法选择的是误差平方和突然变小时对应的$k$值。

2）轮廓系数
对于第$i$个对象，计算它到簇中所有其他对象的平均距离，记作$a_i$
对于第$i$个对象和不包含该对象的任意簇，计算该对象到给定簇中所有对象的平均距离，关于所有的簇，找出最小值，记作$b_i$

样本点$i$的轮廓系数：
$s(i)=\frac{b(i)?a(i)}{max(a(i),b(i))}$

轮廓系数$S$越接近于1，聚类效果越好。

7. Kmeans的优缺点

优点：
1）算法简单
2）适用于球形簇
3）二分k均值等变种算法运行良好，不受初始化问题的影响
缺点：
1）不能处理非球形簇、不同尺寸和不同密度的簇
2）对离群点、噪声敏感

8. DBSCAN与k-means比较

1）k均值聚类是基于划分的聚类，DBSCAN是基于密度的聚类
2）k均值聚类需要指定聚类簇数k，并且初始聚类中心对聚类的影响很大。DBSCAN对噪声不敏感，需要指定邻域距离阈值$?$和$MinPts$，可以自动确定簇个数
3）k均值很难处理非球型的簇和不同尺寸的簇，DBSCAN可以处理不同尺寸或形状的簇，不太受噪声、离群点的影响。但是面对不同密度的簇时，两种算法的性能都很差。

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系