[人工智能]【聚类算法】DBSCAN算法及其Python实现

一：DBSCAN算法

（1）快速入门BCSCAN算法

如下是一组未被聚类的数据

可以用肉眼进行大致划分

• 绿色为第一类
• 蓝色为第二类
• 灰色为离群点

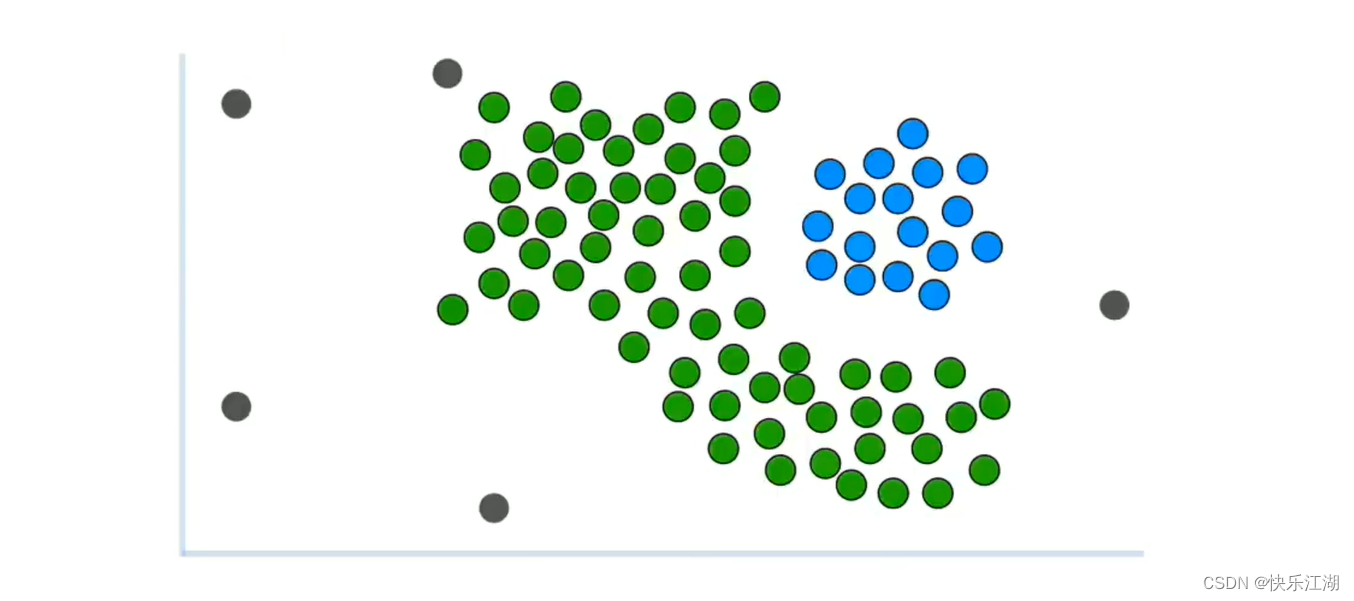
这种非凸数据是无法用K-Means算法进行区分的，如果使用则效果会是这样

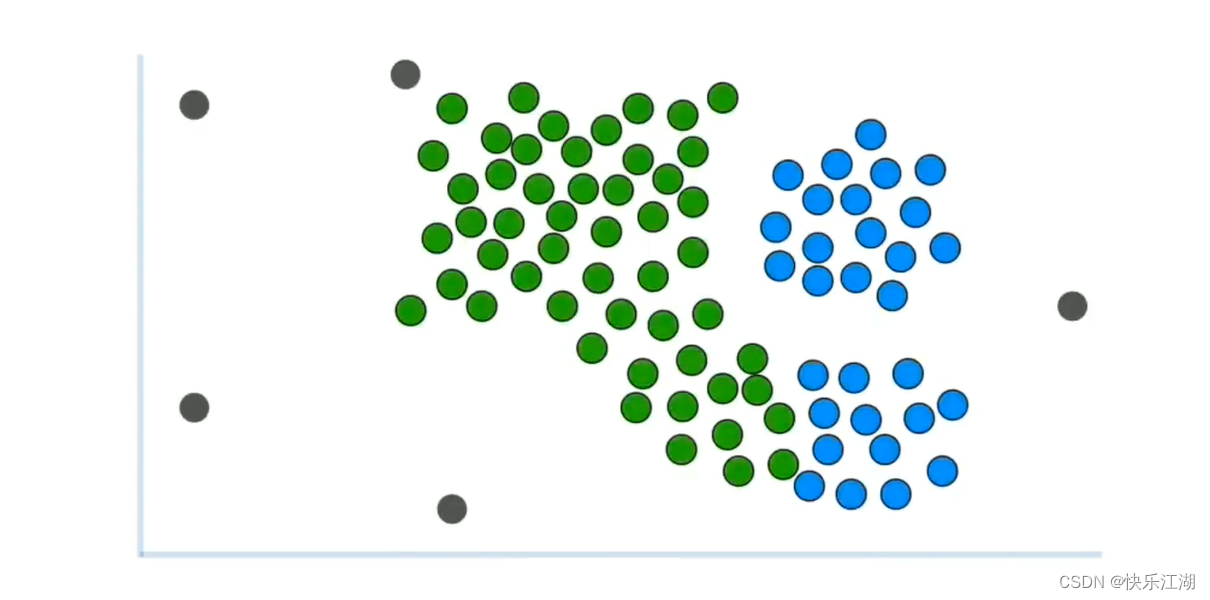
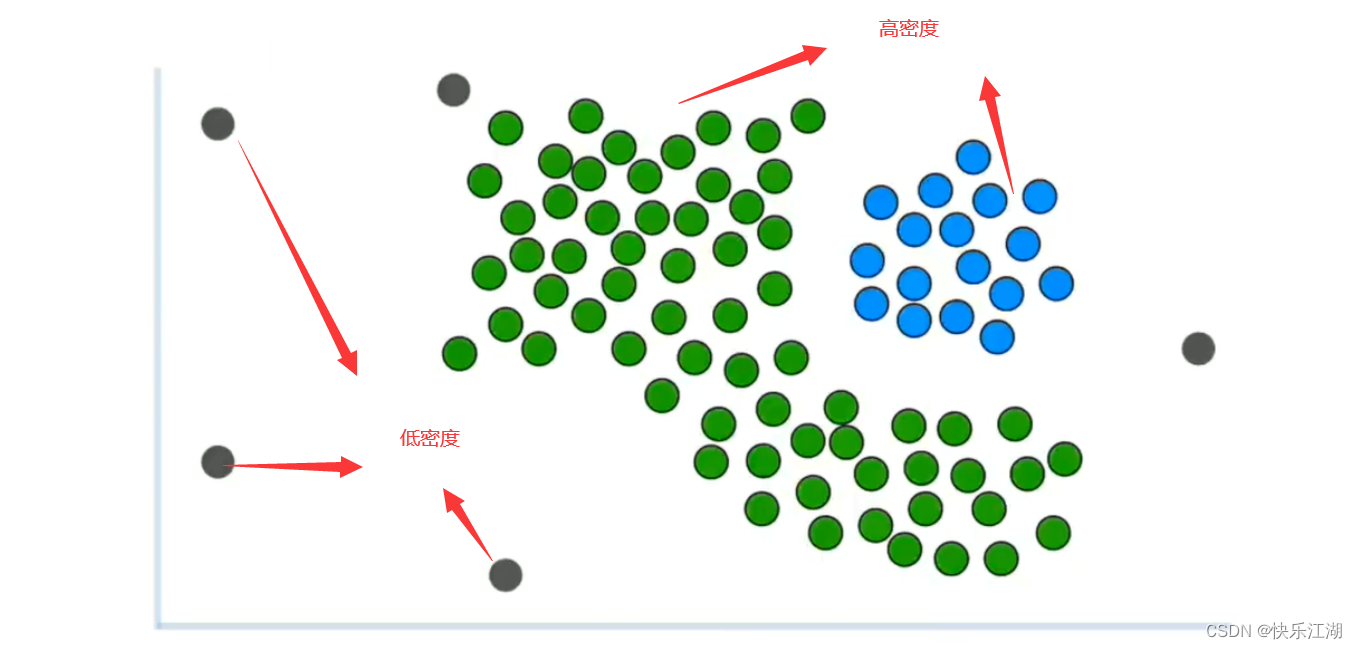
而本节的DBSCAN算法可以解决这个问题。DBSCAN算法通过密度来识别簇

• 簇通常位于高密度区域
• 离群值通常位于低密度区域

核心点是DBSCAN算法中非常重要的点，一个点是否能够成为核心点关键在于该点周围的临近点个数是否大于等于某个$r$值（称为半径，需要自己提前设定）

• 例如下图，定义这个$r$值为4，那么第1-4个点可以作为核心点，但第5-6个点不可以

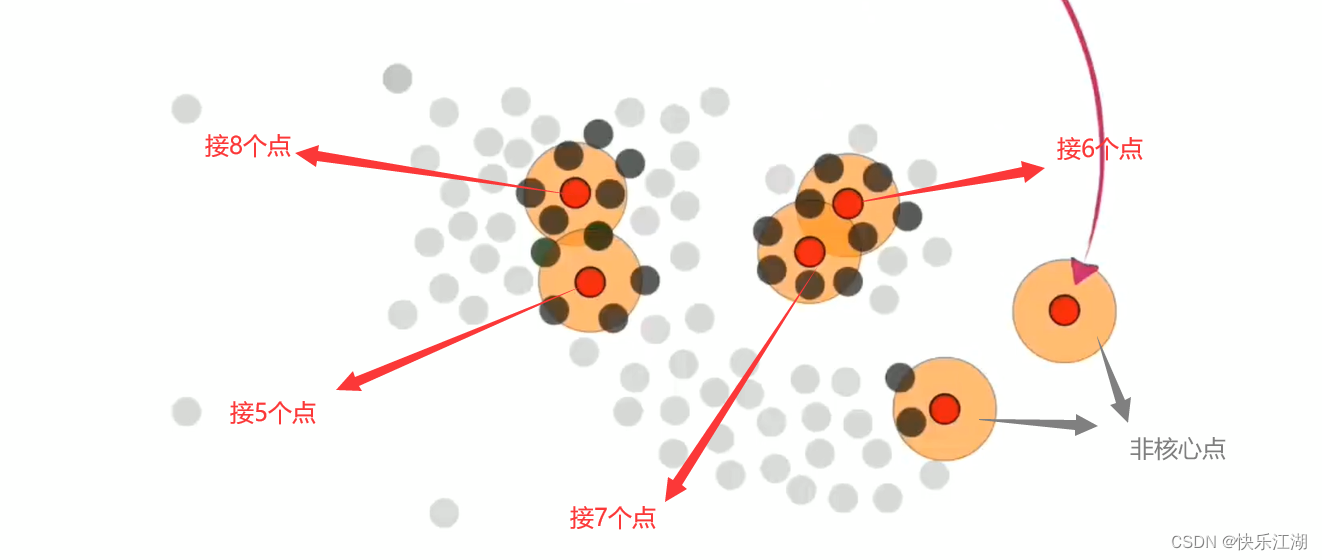
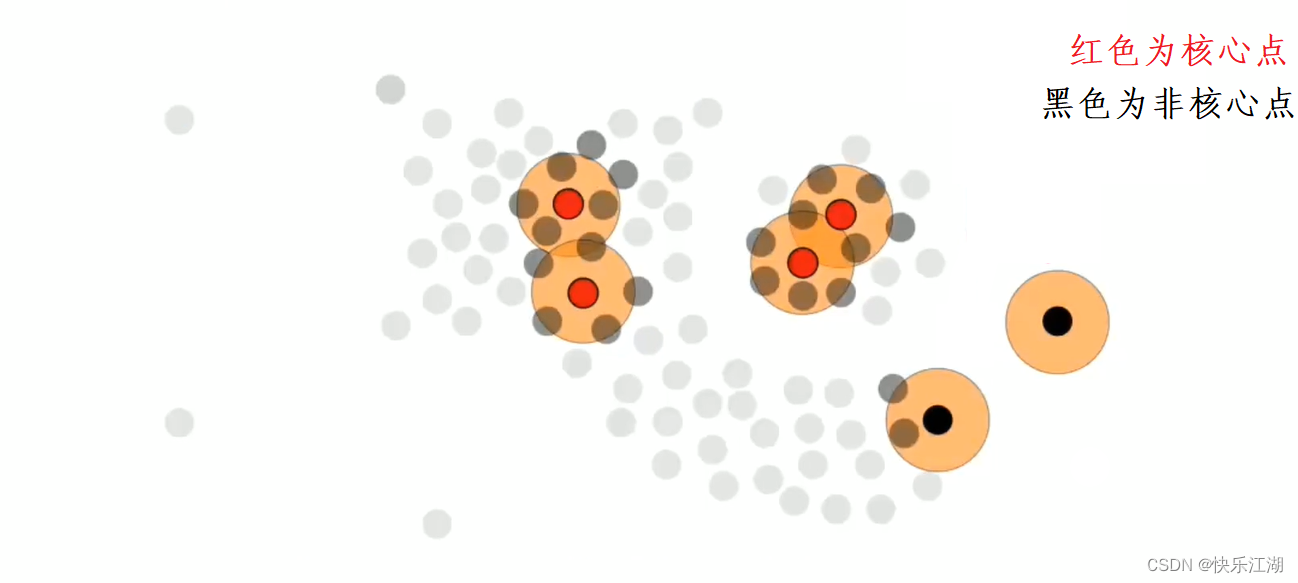
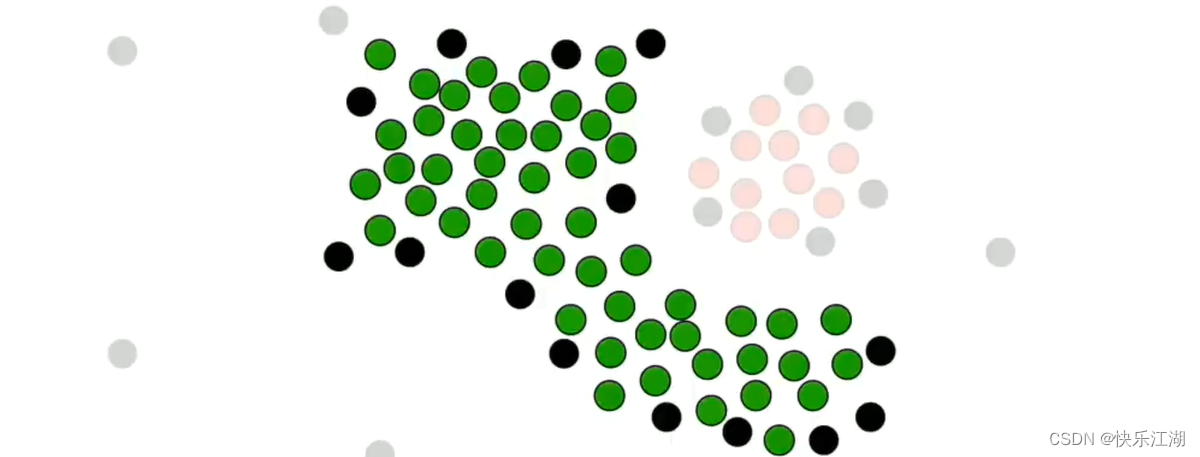
接着，我们挑选这组数据的所有核心点和非核心点

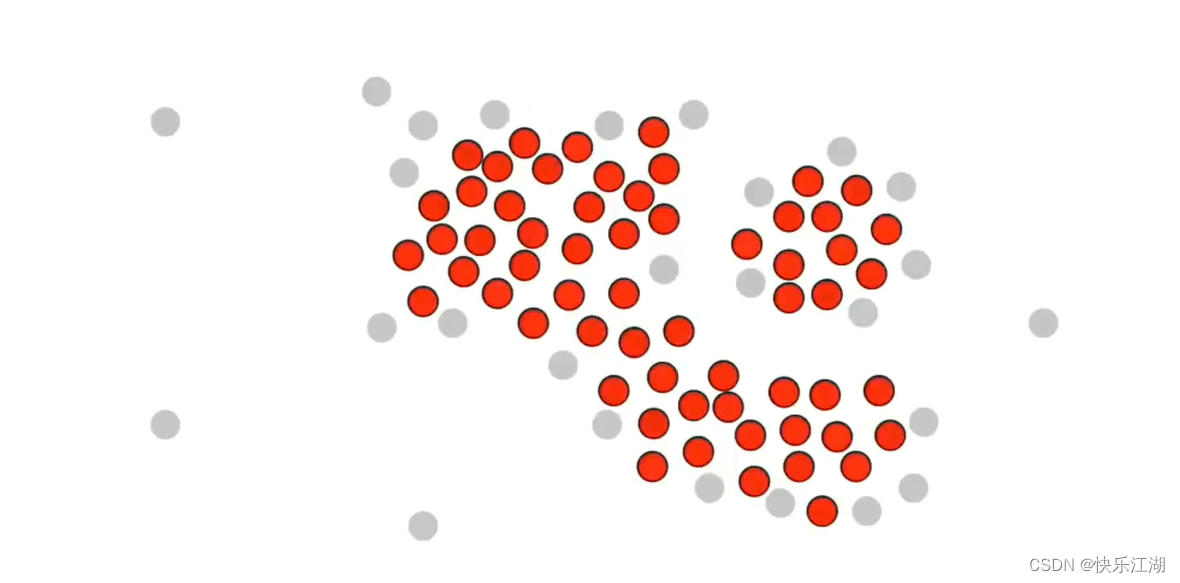
然后在核心点中随机选取一个并标记为绿色，然后把该绿色点周围的所有核心点都加入到该簇中，也标记为绿色

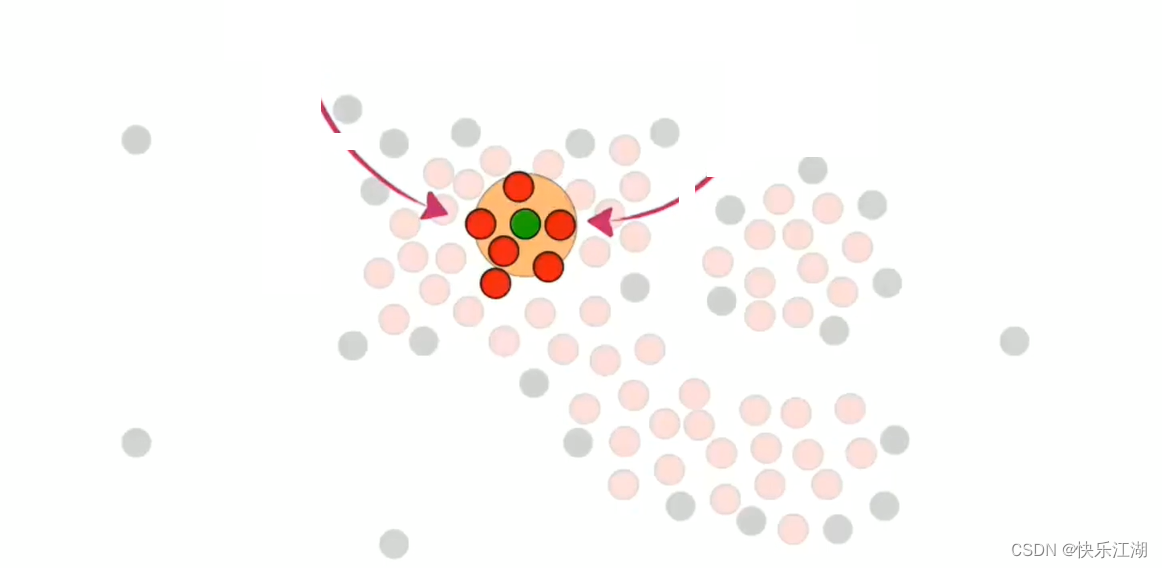
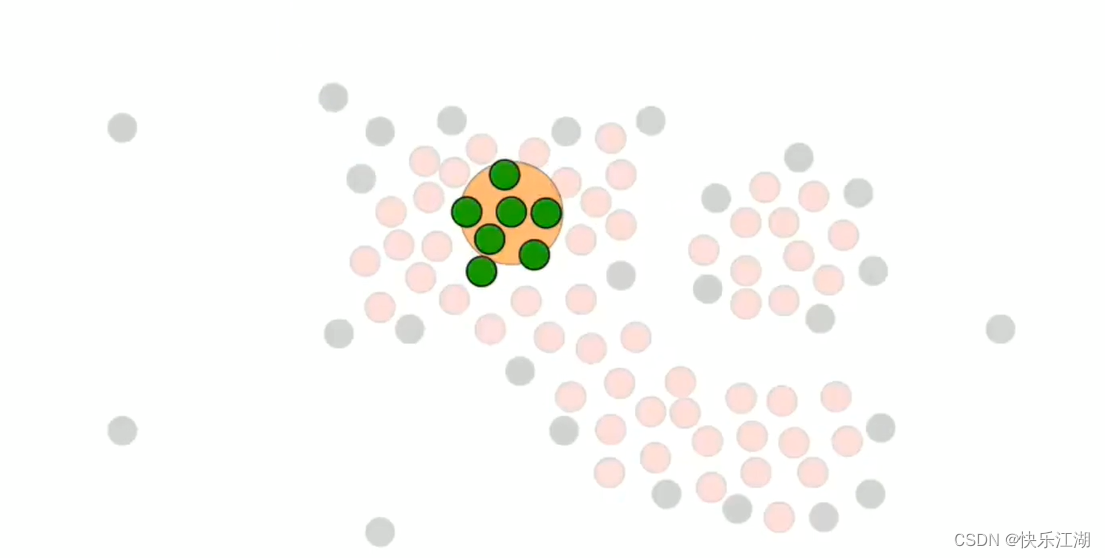
然后对其他绿色点执行重复操作

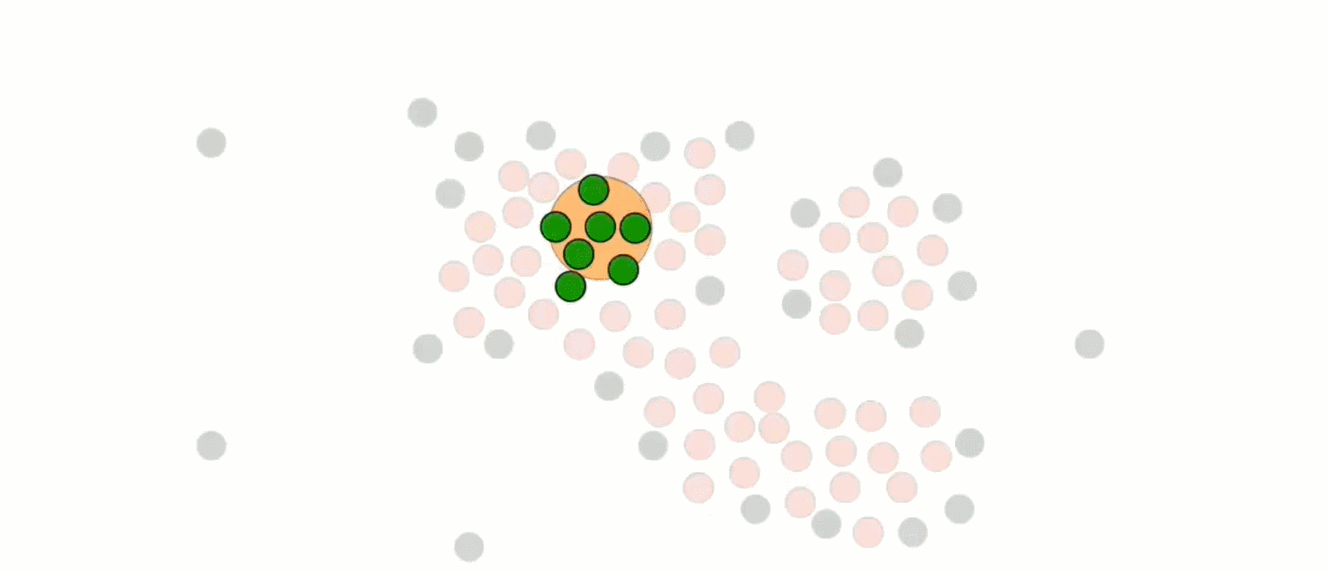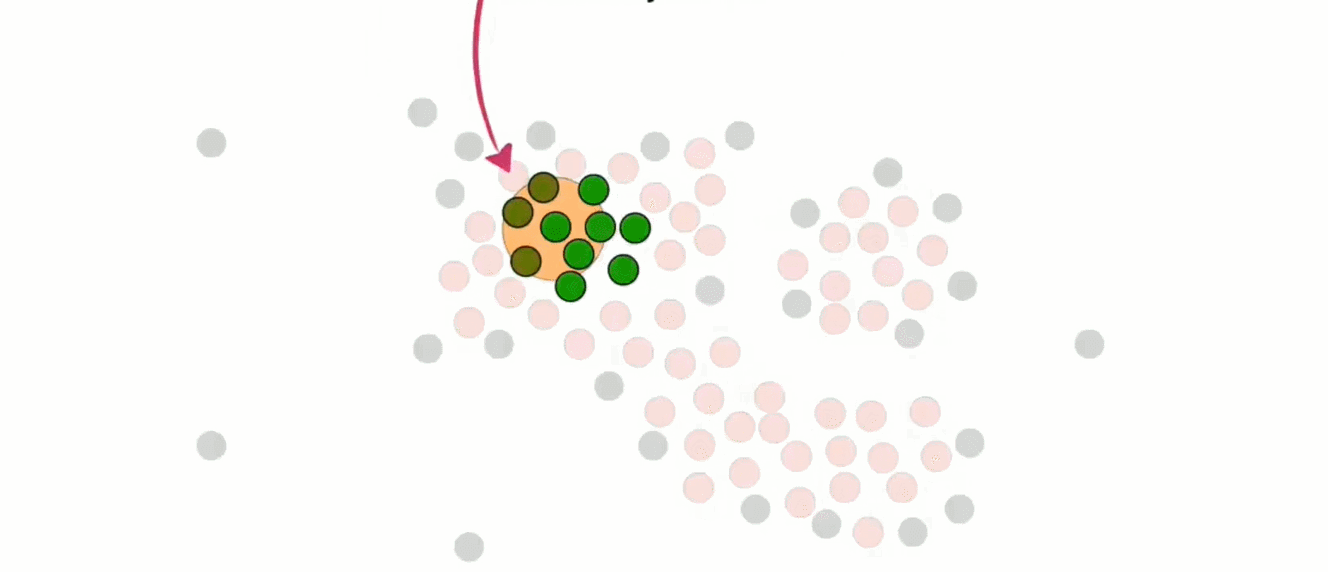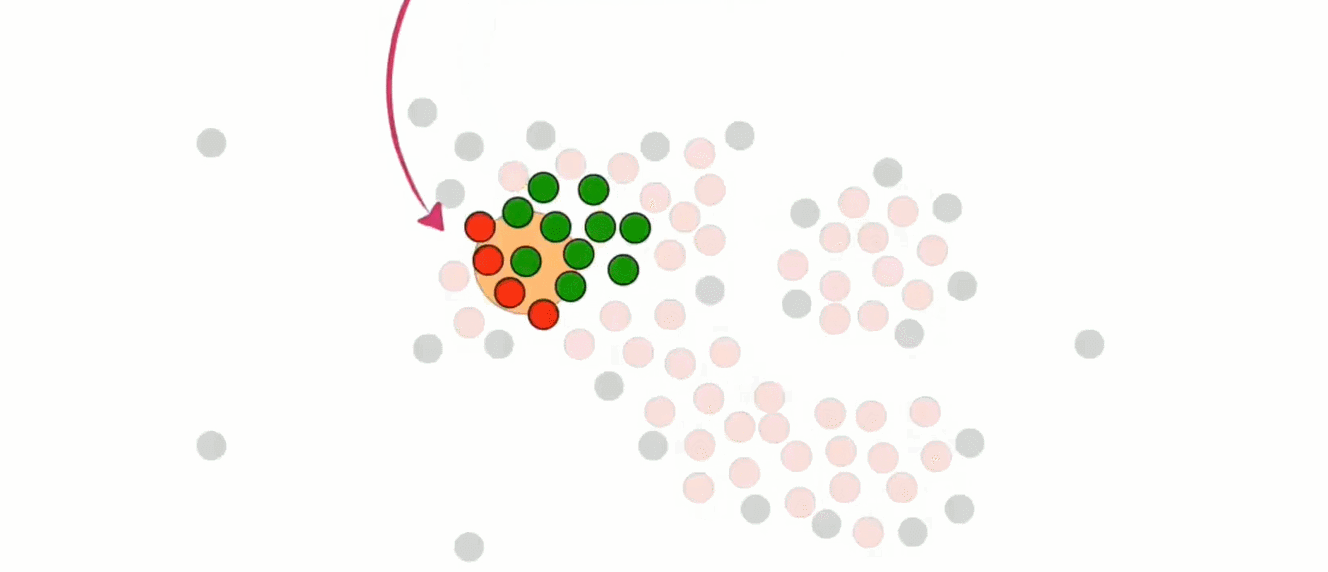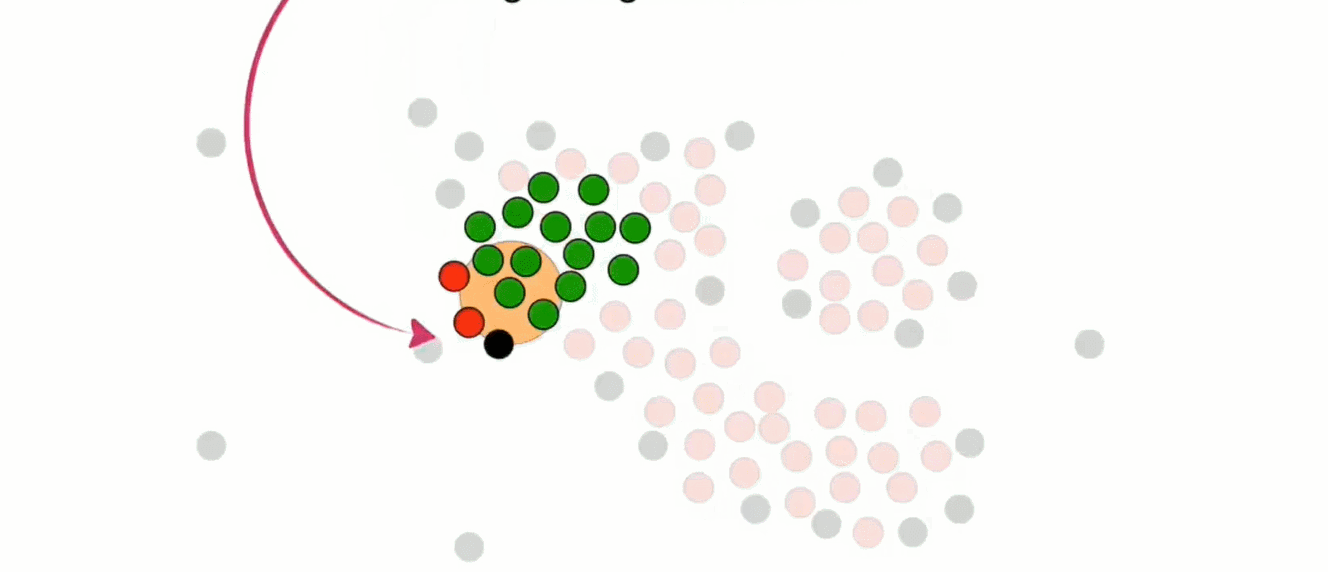
在处理时，如果同时喷到了核心点和非核心点，则暂时只把核心点加入其中

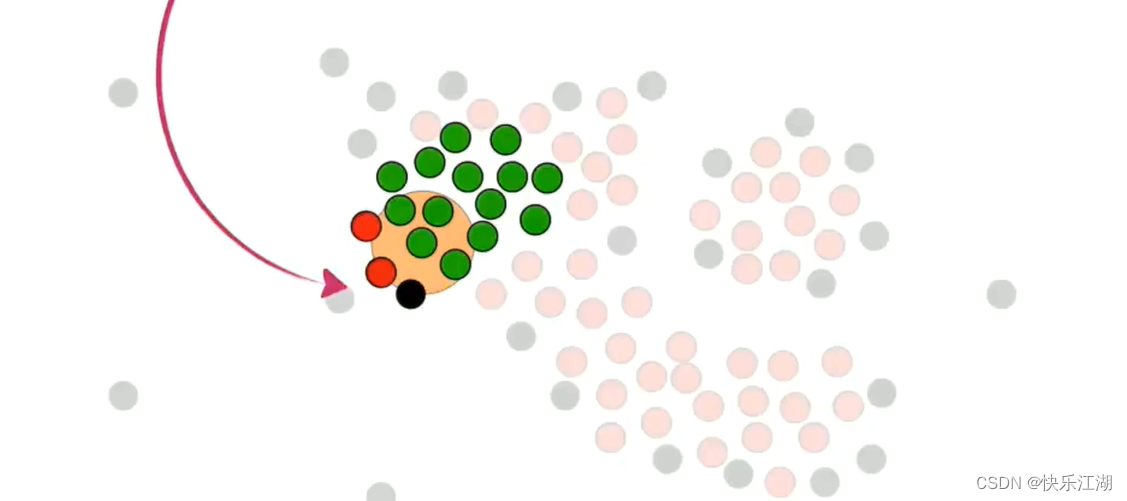
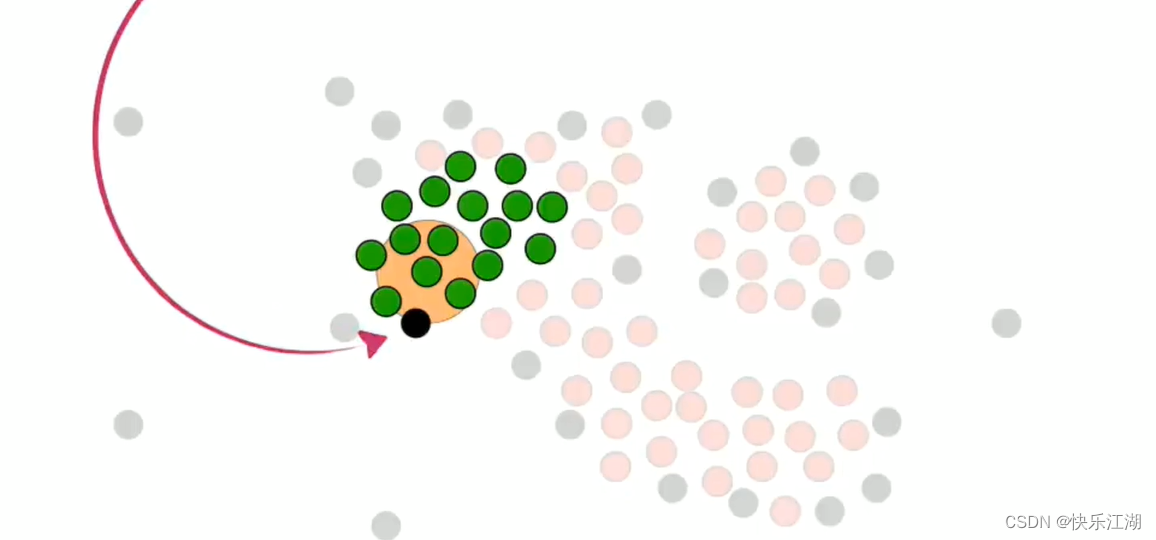
依据这个策略，进行扩展

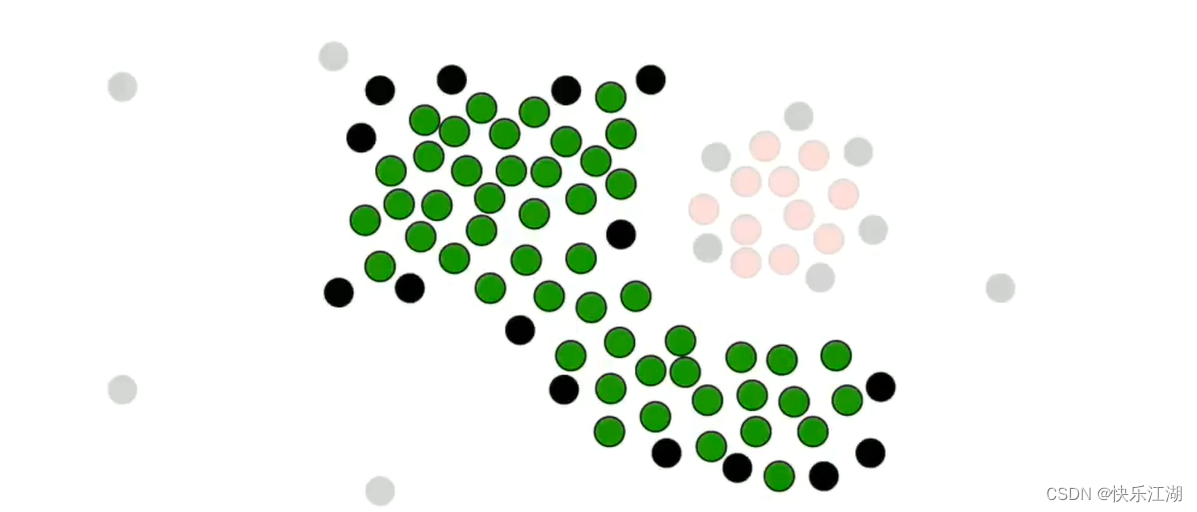
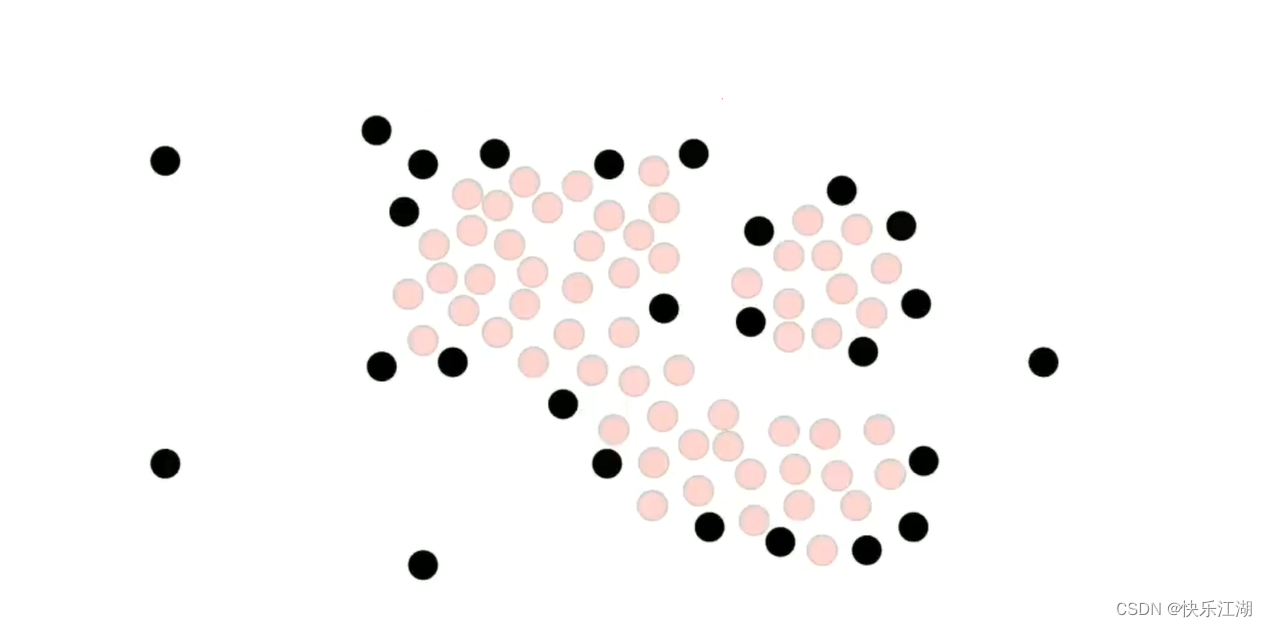
然后处理非核心点。如下对于这个非核心点，其周围存在属于第一个簇的核心点，所以他可以并入

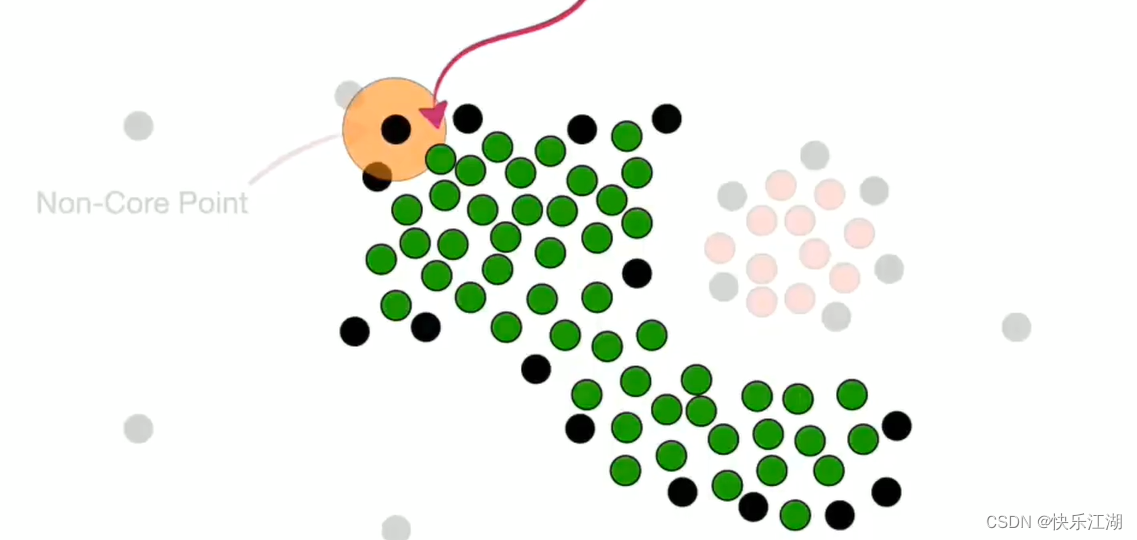
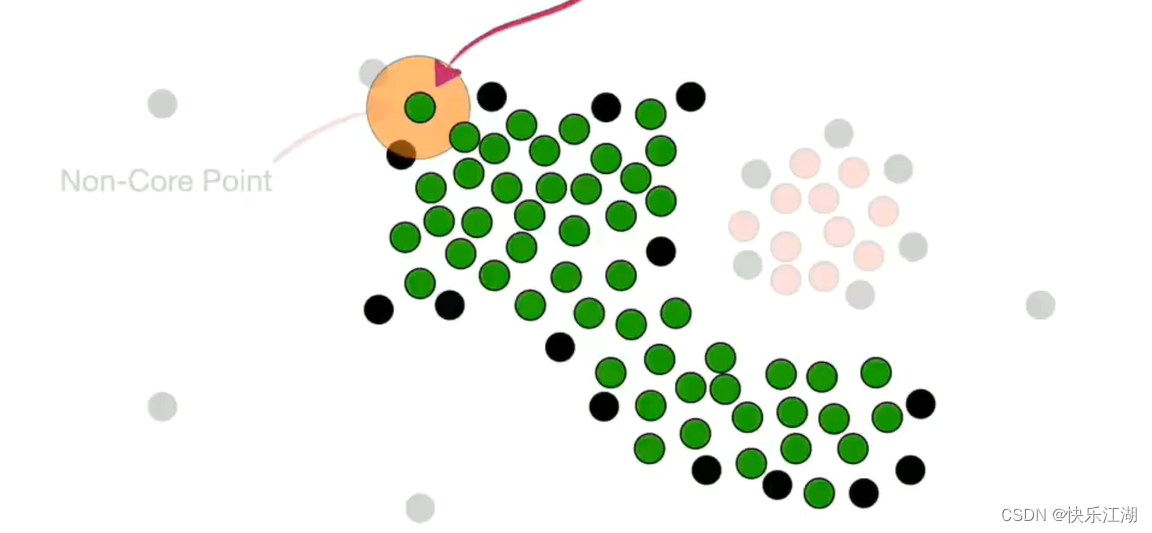
但是该非核心点上面的那个点现在就不可以并入了，或者说这就是它的边界

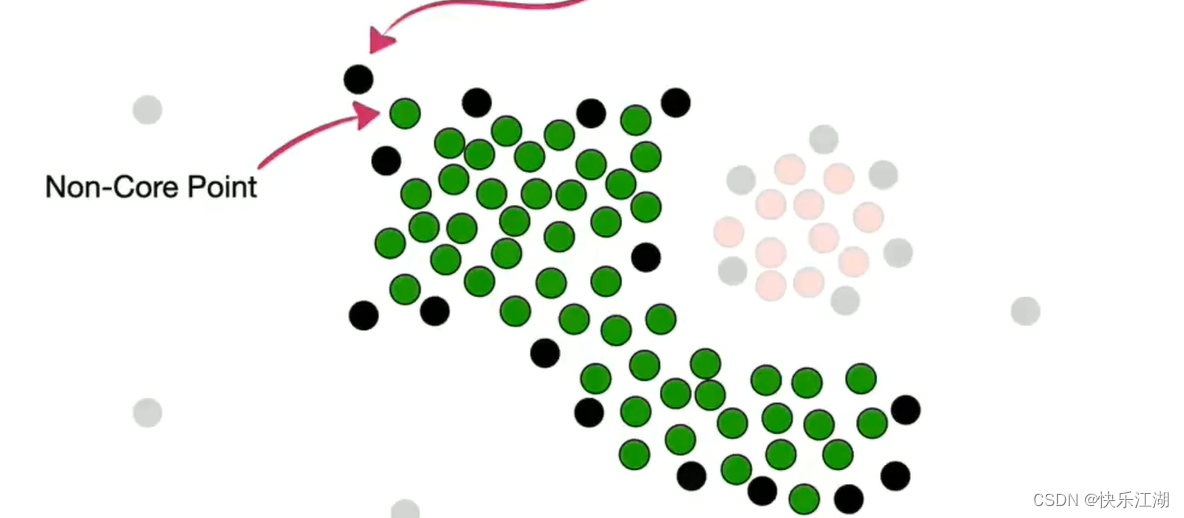
按照这个规则把所有非核心点并入，第一个簇完毕

（2）算法简介

A：基本概念

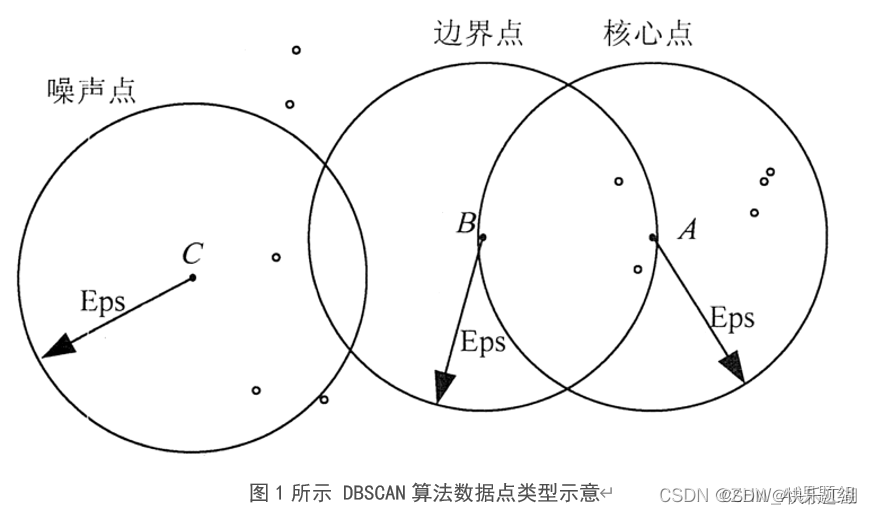
基本概念：DBSCAN全称为Density-Based Spatial Clustering of Applications with Noise，也即基于密度的带有噪声点的聚类方法。该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据中发现任意形状的簇，它将簇定义为密度相连的点的最大集合；在DBSCAN算法中将数据点分为以下3类

• 核心点： 如果一个对象在其半径Eps内含有超过MinPts数目的点，则该对象为核心点
• 边界点： 如果一个对象在其半径Eps内含有点的数量小于MinPts，但是该对象落在核心点的邻域内，则该对象为边界点
• 噪声点： 如果一个对象既不是核心点也不是边界点，则该对象为噪声点

其中Eps和MinPtS是DBSCAN算法中的两个重要参数

• Eps：定义密度时的邻域半径
• MinPts：定义核心点时的阈值

如下图所示，假设MinPts设置为5，箭头表示Eps范围，则：

• $A$是核心点：因为在其Eps邻域内有7个点
• $B$是边界点：因为它落在了$A$的Eps邻域内
• $C$是噪声点：没有落在任何核心点的邻域内

B：直接密度可达、密度可达、密度相连

直接密度可达：如果点$p$在核心点$q$的$Eps$邻域内，则称数据对象$p$从数据对象$q$出发是直接密度可达的

• 注意是$p$直接可达$q$，但不能是$q$直接可达$p$，除非$q$也是核心点

密度可达：如果存在数据对象链($p_1$, $p_2$, … , $p_n$ , $p_{n+1}$)，其中$p_{i+1}$是从$p_i$关于$Eps$和$MinPts$直接密度可达的，则称数据对象$p_n$是从数据对象$p_1$关于$Eps$和$MinPts$密度可达的

• 实际上直接密度可达的“传播”

密度相连：若从某核心点$p$出发，点$q$和点$k$都是密度可达的，那么$q$和$k$就是密度相连的

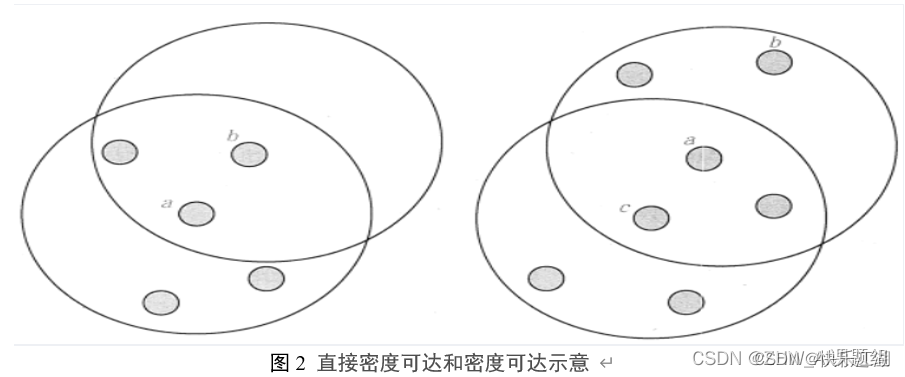
如下图：

• 左图：点$a$为核心点，点$b$为边界点，所以$a$直接密度可达$b$（但$b$不直接可达$a$，$b$不是核心点）
• 右图： $c$直接密度可达$a$，$a$直接密度可达$b$，所以$c$密度可达$b$

（3）算法流程

A：流程

DBSCAN输入为

• 参数$D$：输入的数据集
• 参数$\epsilon$：邻域半径
• 参数$MinPts$：密度阈值

其中$\epsilon$和$MinPts$这两个参数的选择非常重要，选择时可以参考如下方法，但是在实际使用时通常时多次尝试即可

• $\epsilon$：可以根据距 $K$距离来设定，找出 突变点（$K$距离：对于给定的数据集$P$= { p 1 , p 2 , . . . , p n } \{p_{1}, p_{2} , ... , p_{n}\} {p1?,p2?,...,pn?}，计算点$p(i)$到数据集$D$的子集$S$中所有点之间的距离，距离按从小到大的顺序排序，则$d(k)$就称之为$K距离$）
• $MinPts$：一般情况下小一点合适

算法流程如下，整体来说还是很容易理解的

B：演示

现在以下面的样本数据为例，演示DBSCAN算法工作流程

• $\epsilon$= 3
• $MinPts$ = 3

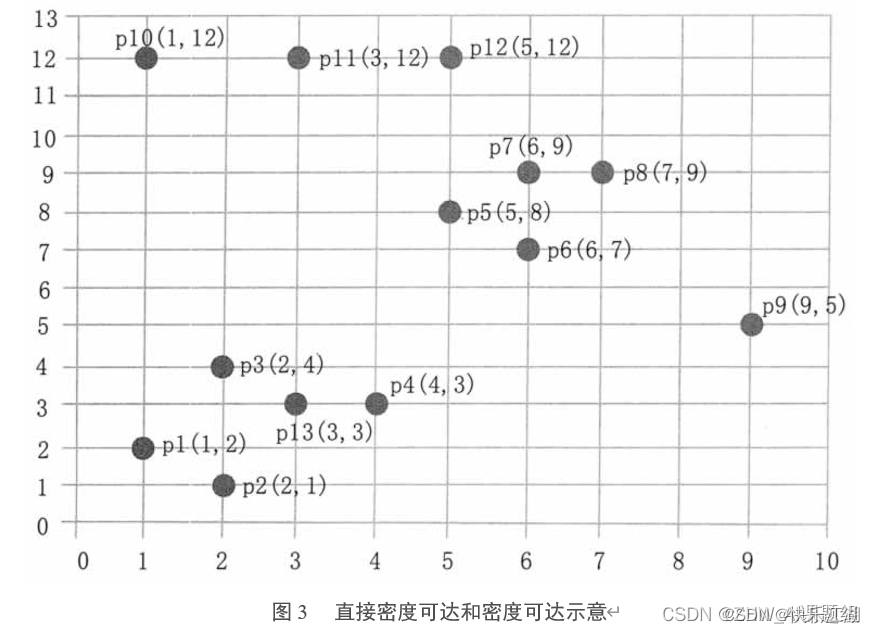
步骤①： 顺序扫描数据集样本点，首先取到$p1(1,2)$

1. 计算每一点到$p1$的距离，例如$d(p1,p2)=1.414$
2. 根据每个样本点到$p1$的距离和所设邻域$\epsilon$= 3，得到$p1$的$Eps$邻域为 { p 1 , p 2 , p 3 , p 13 } \{p1, p2, p3, p13\} {p1,p2,p3,p13}
3. 所设$Minpts$=3，而$p1$的$Eps$邻域有4个点，所以$p1$为核心点
4. 因此以$p1$为核心点建立簇$C_1$，找出所有从$p1$密度可达的点（$p1$邻域内的点都是$p1$直接密度可达的点，所以都属于$C_1$）
5. $p2$的邻域为$(p1,p2,p3,p4,p13)$，且$p1$直接密度可达$p2$、$p2$直接密度可达$p4$，所以$p1$密度可达$p4$，因此$p4$也属于$C_1$
6. $p3$、$p4$、$p13$也是核心点，其其邻域的点已经都在$C_1$中了
7. 于是，以$p1$为核心点出发的那些密度可达的对象全部处理完毕，得到簇$C_1$，包含对象$(p1,p2,p3,p4,p13)$

步骤②： 继续顺序扫描数据样本点，取到$p5(5,8)$

1. 计算$p5$邻域，其$Eps$邻域为$(p5,p6,p7,p8)$，由于有4个点，所以$p5$是核心点
2. 以$p5$为核心点建立簇$C_2$，找出所有从$p5$密度可达的点，得到簇$C_2$，包含点$(p5,p6,p7,p8)$

步骤③： 继续顺序扫描数据集样本点取到$p9(9,5)$

• $p9$其$Eps$邻域内只有一个点，所以不是核心点

步骤④： 继续顺序扫描数据集样本点取到$p10(1,12)$

• 同理，$p10$并不是核心点

（4）Python实现

A：算法代码

import random
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd


def dbscan(data_set, eps, min_pts):
    examples_nus = np.shape(data_set)[0]  # 样本数量
    unvisited = [i for i in range(examples_nus)]  # 未被访问的点
    visited = []  # 已被访问的点
    # cluster为输出结果，表示对应元素所属类别
    # 默认是一个长度为examples_nus的值全为-1的列表，-1表示噪声点
    cluster = [-1 for i in range(examples_nus)]

    k = - 1  # 用k标记簇号，如果是-1表示是噪声点
    while len(unvisited) > 0:  # 只要还有没有被访问的点就继续循环
        p = random.choice(unvisited)  # 随机选择一个未被访问对象
        unvisited.remove(p)
        visited.append(p)

        nighbor = []  # nighbor为p的eps邻域对象集合，密度直接可达
        for i in range(examples_nus):
            if i != p and np.sqrt(np.sum(np.power(data_set[i, :]-data_set[p, :], 2))) <= eps:  # 计算距离，看是否在邻域内
                nighbor.append(i)

        if len(nighbor) >= min_pts:  # 如果邻域内对象个数大于min_pts说明是一个核心对象
            k = k+1
            cluster[p] = k  # 表示p它属于k这个簇

            for pi in nighbor:  # 现在要找该邻域内密度可达
                if pi in unvisited:
                    unvisited.remove(pi)
                    visited.append(pi)

                    # nighbor_pi是pi的eps邻域对象集合
                    nighbor_pi = []
                    for j in range(examples_nus):
                        if np.sqrt(np.sum(np.power(data_set[j]-data_set[pi], 2))) <= eps and j != pi:
                            nighbor_pi.append(j)

                    if len(nighbor_pi) >= min_pts:  # pi是否是核心对象，通过他的密度直接可达产生p的密度可达
                        for t in nighbor_pi:
                            if t not in nighbor:
                                nighbor.append(t)
                if cluster[pi] == -1:  # pi不属于任何一个簇，说明第pi个值未改动
                    cluster[pi] = k
        else:
            cluster[p] = -1  # 不然就是一个噪声点
    return cluster

B：可视化输出代码

• 以下面的三个圆圈数据集为例

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from DBSCAN import dbscan

#  数据处理
data_types = [0.0000000e+00, 1.0000000e+00, 2.0000000e+00, 3.00E+00]
raw_data = pd.read_csv('./threecircles.csv', header=None)
raw_data.columns = ['X', 'Y', 'Type']
x_axis = 'X'
y_axis = 'Y'

examples_num = raw_data.shape[0]  # 样本数量
train_data = raw_data[[x_axis, y_axis]].values.reshape(examples_num, 2)  # 搞成数组

#  K距离图绘制函数
def select_minpts(data_set, k):
    k_dist = []
    for i in range(data_set.shape[0]):
        dist =  (((data_set[i] - data_set)**2).sum(axis=1)**0.5)
        dist.sort()
        k_dist.append(dist[k])
    return np.array(k_dist)

#  参数选择

# k = 3  # 取2*2-1
# k_dist = select_minpts(train_data, k)  # K距离
# k_dist.sort()  # 排序（默认升序）
# plt.plot(np.arange(k_dist.shape[0]), k_dist[::-1])  # 绘制K距离图，绘图时从大到小
# plt.show()

eps = 0.07  # 邻域半径
min_pts = 4  # 核心对象
cluster = dbscan(train_data, eps, min_pts)
print(cluster)

plt.figure(figsize=(15, 7), dpi=80)

# 第一幅图已知标签
plt.subplot(1, 2, 1)

for data_types_index in data_types:
    plt.scatter(raw_data[x_axis][raw_data['Type'] == data_types_index], raw_data[y_axis][raw_data['Type'] == data_types_index], label=str(data_types_index))
plt.title('label know')
plt.legend()


# 第二幅图聚类结果
plt.subplot(1, 2, 2)

class1_X = []
class1_Y = []
class2_X =[]
class2_Y =[]
class3_X =[]
class3_Y =[]
noise_X = []  # 噪声点
noise_Y = []  # 噪声点

for index, value in enumerate(cluster):
    if value == 0:
        class1_X.append(raw_data[x_axis][index])
        class1_Y.append(raw_data[y_axis][index])
    elif value == 1:
        class2_X.append(raw_data[x_axis][index])
        class2_Y.append(raw_data[y_axis][index])
    elif value == 2:
        class3_X.append(raw_data[x_axis][index])
        class3_Y.append(raw_data[y_axis][index])
    elif value == -1:
        noise_X.append(raw_data[x_axis][index])
        noise_Y.append(raw_data[y_axis][index])


plt.scatter(class1_X, class1_Y, c='g', label='class1')
plt.scatter(class2_X, class2_Y, c='r', label='class2')
plt.scatter(class3_X, class3_Y, c='blue', label='class3')
plt.scatter(noise_X, noise_Y, c='black', label='noise')
plt.title('DBSCAN')
plt.legend()
plt.show()

（5）聚类效果展示

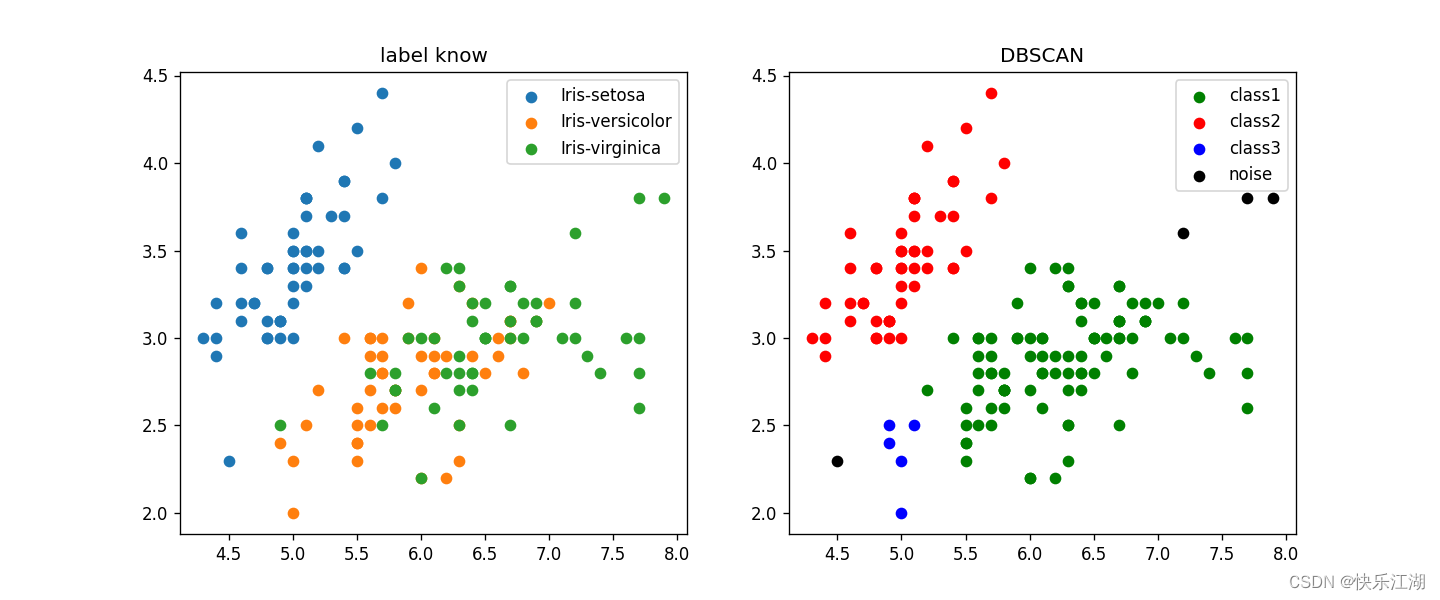
①：鸢尾花数据集

• eps = 0.35
• min_pts = 4

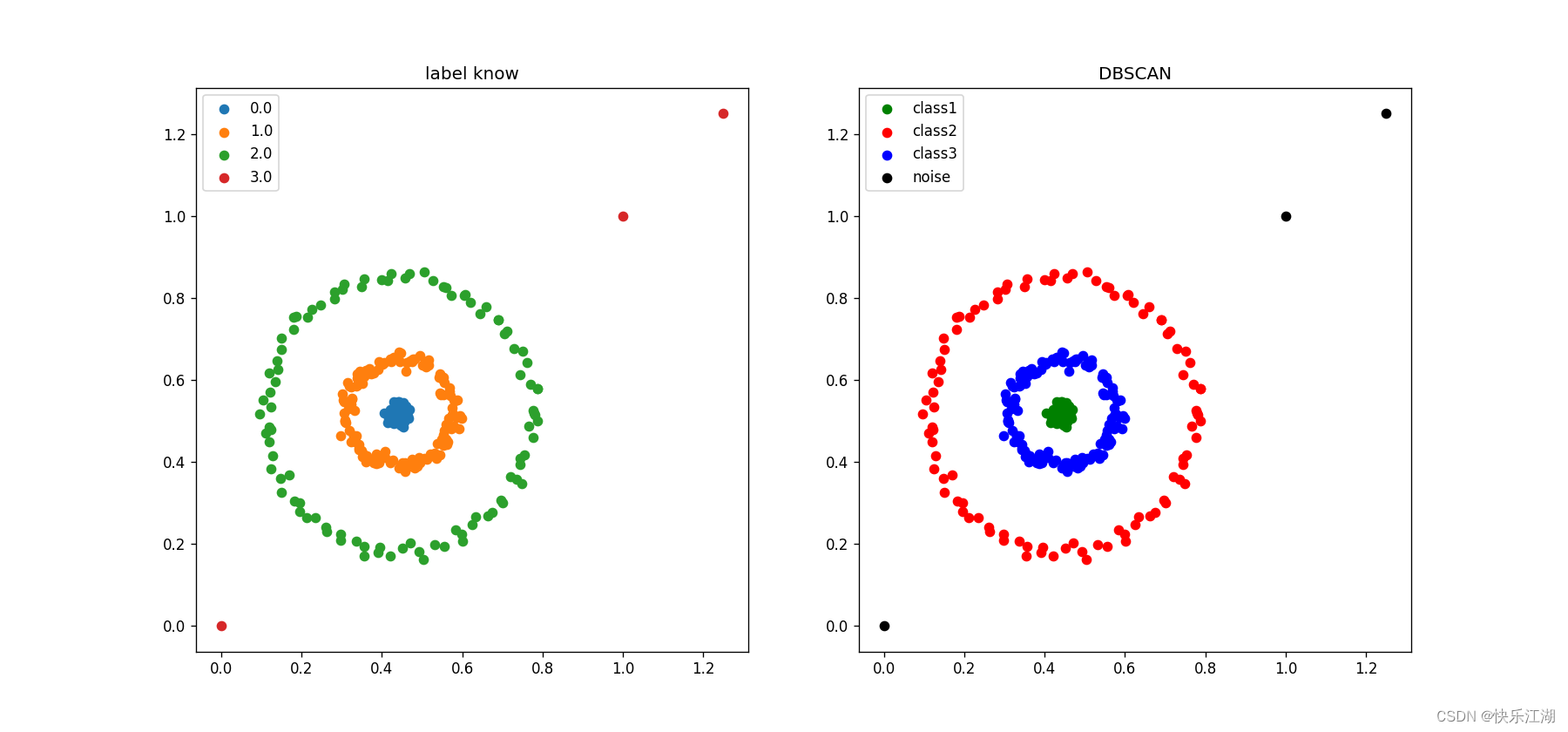
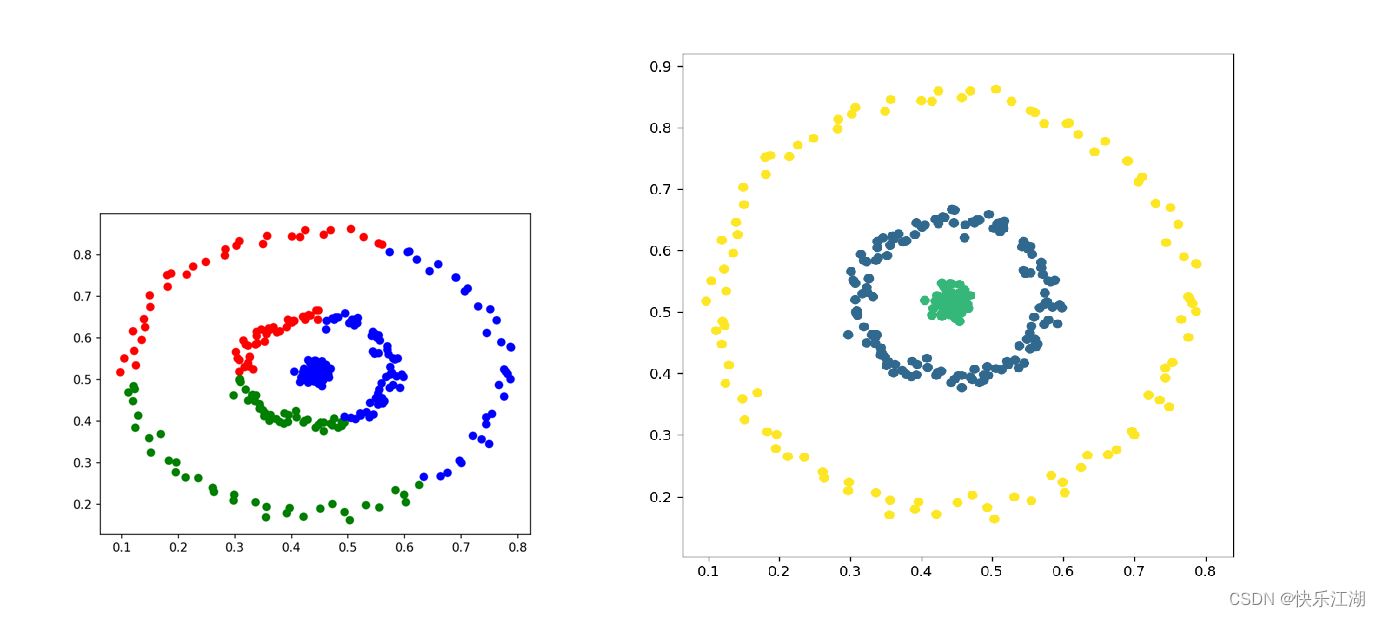
②：三个圆圈数据集（K-Means实现效果差）

• eps = 0.07
• min_pts = 4

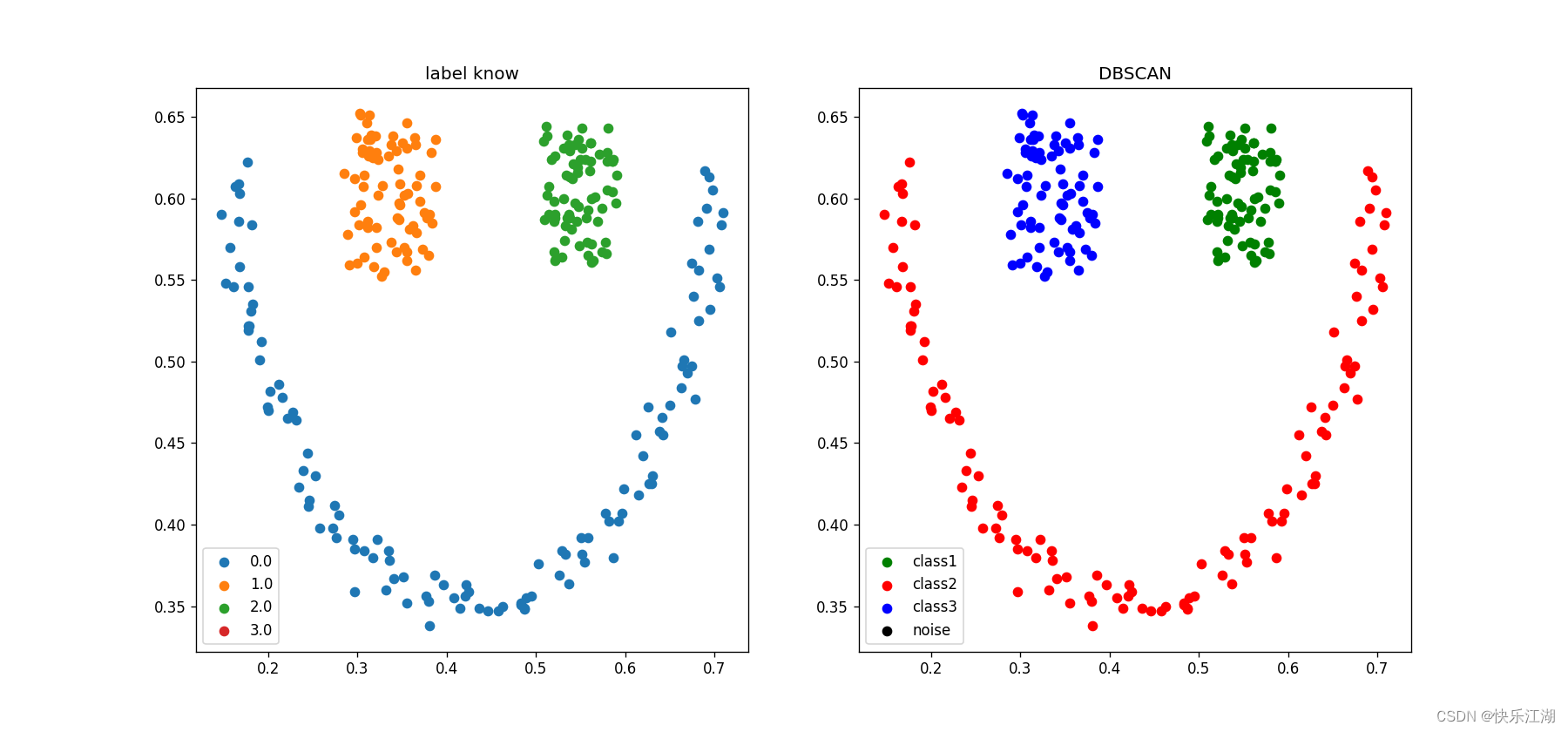
③：笑脸数据集（K-Means实现效果差）

• eps = 0.05
• min_pts = 4

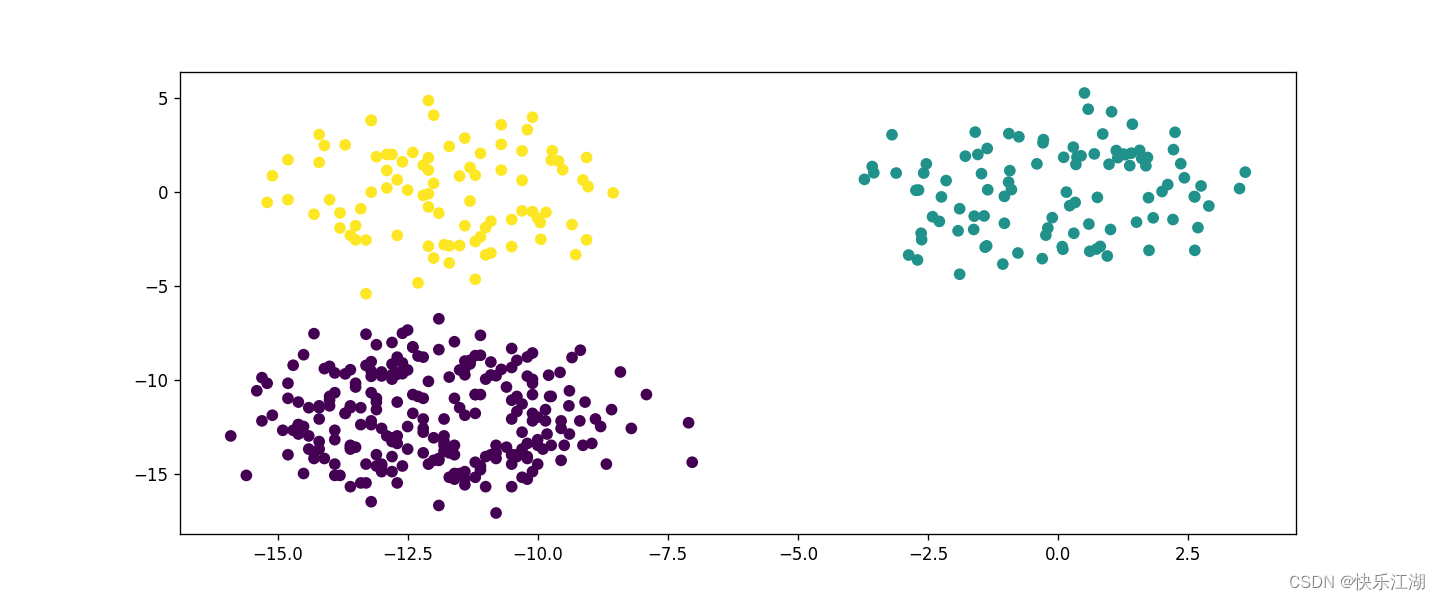
④：人造数据集

• 438个数据，分为三类（提前不知道标签）
• eps = 1.8
• min_pts = 4

⑤：西瓜数据集

• eps = 0.08
• min_pts = 2

二：DBSCAN算法探讨

（1）算法优缺点

A：优点

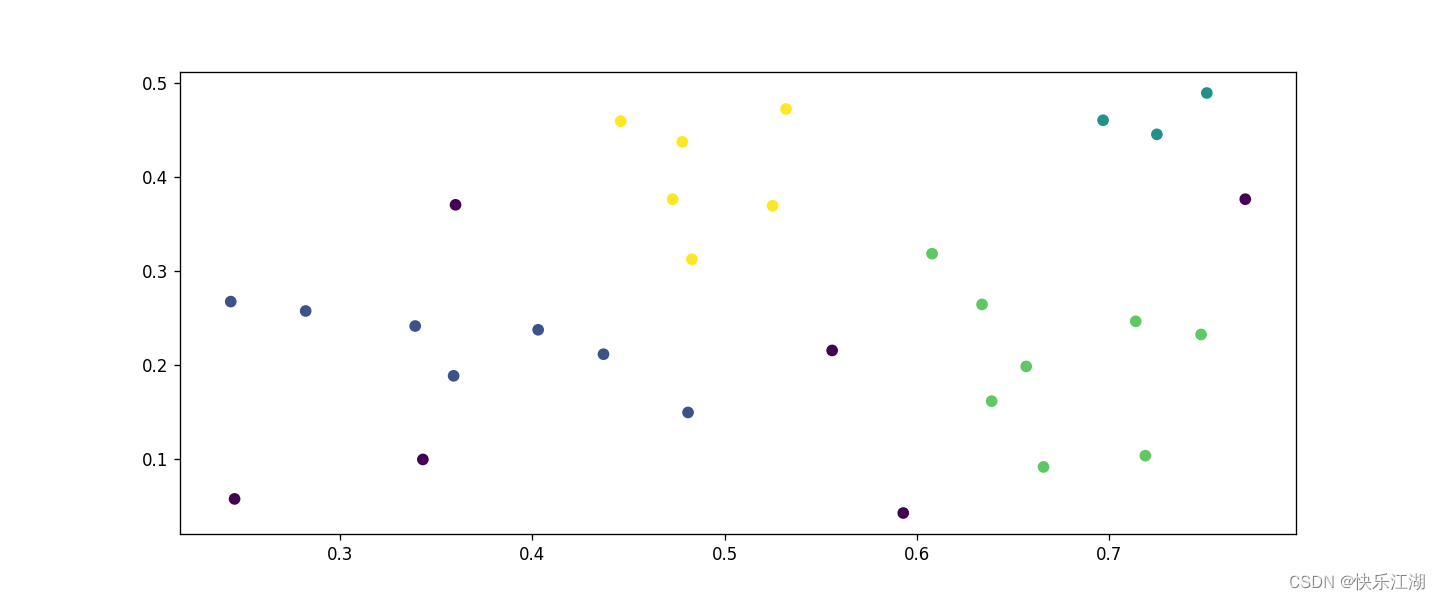
①：可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集

②：可以在聚类的同时发现异常点，对数据集中的异常点不敏感

③：不需要指定簇数，并且多次实验结果往往是相同的

B：缺点

①：如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合

②：调参相较于K-Means复杂一点，不同参数组合对聚类效果有很多影响

（2）参数选择

A：参数选择原则（快速）

• min_pts：一般选择维度+1或者维度×2即可
• eps：如果所分的类少了，那就把eps调小一点；如果所分的类多了，那就把eps调大一点

B：调参确定

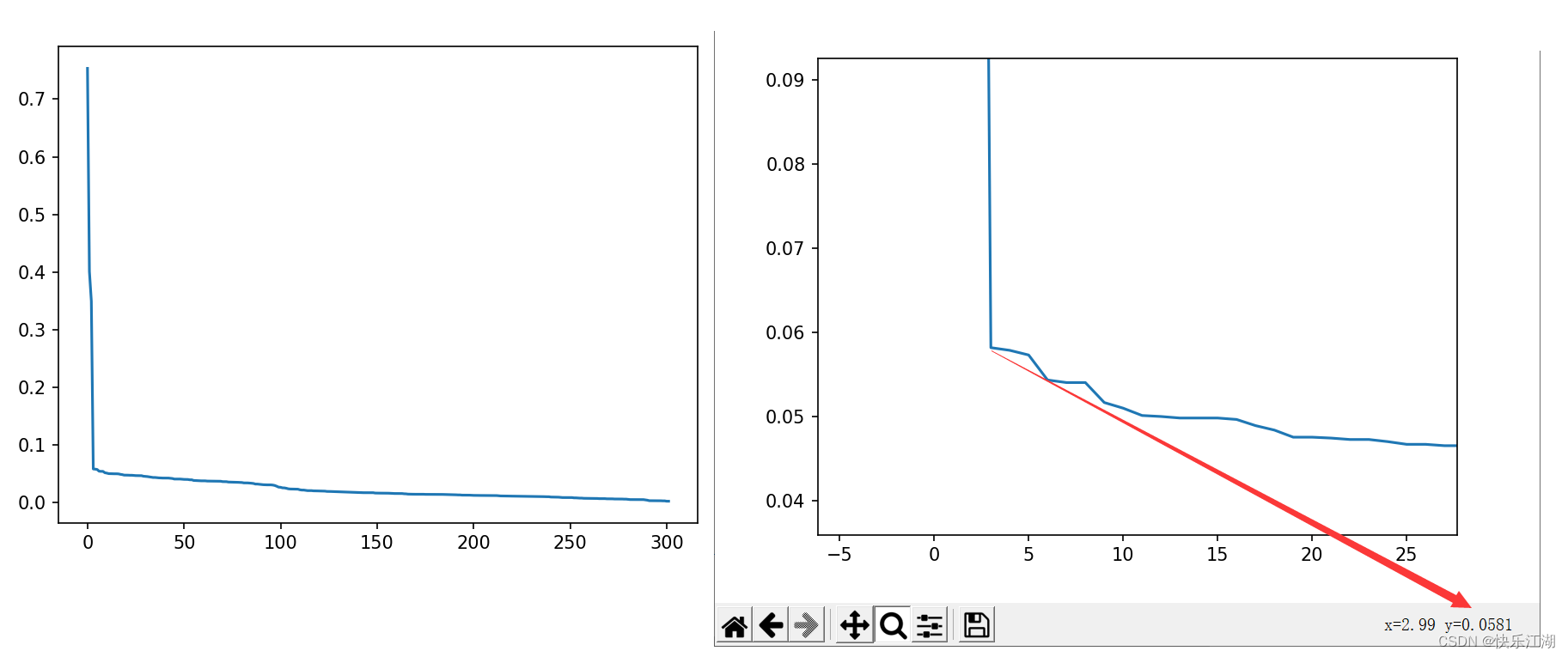
前面说过，eps可以根据K-dist图（K距离图）确定。这里的K-dist是指，从某个点$P$到第$K$个与它最近的点的距离的值，然后将这些距离从小到大排序后绘图，称为K-dist图，其中拐点位置即为eps的值

• 因为在拐点位置往往遇到了边界点或者噪声点

调参步骤如下

1. 确定K值，一般取2*维度-1
2. 绘制K-dist图
3. 拐点位置（波动最大的地方）为eps（可以取多个拐点尝试）
4. min_pts可以取K+1

k = 3  # 取2*2-1
k_dist = select_minpts(train_data, k)  # K距离图
k_dist.sort()  # 排序（默认升序）
plt.plot(np.arange(k_dist.shape[0]), k_dist[::-1])  # 绘图时从大到小
plt.show()

如下eps建议取0.0581

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系