公众号原文
ArcGIS与地理加权回归GWR【一】https://mp.weixin.qq.com/s/fMPYxO3G7ff2192ZQICN-A
开个新坑啊,写一写关于地理加权回归基础的东西(深了我也不会啊),希望也能用通俗的语言来记录一下我以前学习空间统计过程中的理解。

1. 传统线性回归
不管你有没有系统学习过,对于线性回归,相信多少都有那么点了解。回归分析实质上就是研究一个或多个自变量X对一个因变量Y的影响关系情况,如研究各地房价影响因素。X1-Xn是n个自变量,β0-βn是未知参数,可以使用最小二乘法进行估计,即β0-βn的最小二乘估计(那个β尖符号)。当自变量为1个时,是一元线性回归,自变量为2个及以上时,称为多元线性回归。
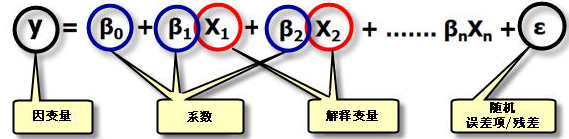
我也不会去深入巴拉一堆我也不专业的数学问题,地理加权回归正是在线性回归的基础上扩展而来,所谓青出于蓝而胜于蓝,那地理加权回归比传统的线性回归蓝在哪啊

一般线性回归都是全局的,由于空间自相关(地理学第一定律)和空间异质性(地理学第二定律)的存在,传统的回归模型不适用于处理地理空间数据。而GWR是在多元线性回归的基础上将数据的地理位置引入到回归系数之中。
2. 全局和局部
然后说明一下”全局回归“和”局部回归“
线性回归可分为全局回归和局部回归,全局回归假定估计系数在全局内是平稳的,回归系数并不随着空间位置的改变而改变,如多元线性回归模型。好比经常说我们疫情防控整体稳中向好(WinWinWin);局部回归认为回归系数是局部光滑的,在全局内回归系数是不同的,有多个值的,好比稳中向好中也有个别地方爆发。如地理加权回归。简单的理解如下图,左边就是全局,右边就是局部。
外地想起四川便是标志性的熊猫与火锅,但在各地市眼里都很有特色
3. 地理篇
来看看地理加权回归中的“地理”,地理位置,没错,地理学第二定律登场:空间异质性,地理现象的空间变化以及变化的差异性,即不可控的空间变化规律。

单纯的举个例子,房价。在一个城市影响房价的因素是多样的,比如在A处,因为紧邻CBD房子卖的贵,在B处的老破小因为旁边有个好学校卖的也贵,在C因为依山傍水环境好所以房子卖的还贵,所以在A处,紧邻CBD这个因素对房价解释度就很强,环境或者学校在A处反而没太有什么关系。

(可能会有人想到对房价产生影响的某些社会经济因素在一个区域的影响力是一样的或者变化非常小可以忽略不计,而某些因素又是变化,这就属于混合地理加权回归模型了,在此请不要想太多)。
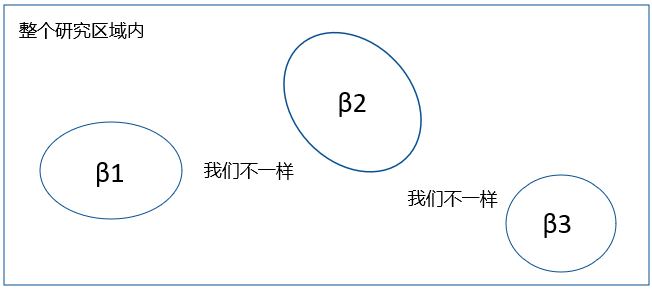
因此,在实际问题研究中我们经常发现回归参数在不同地理位置上往往表现为不同,也就是说回归参数随地理位置变化,这时如果仍然采用全局空间回归模型(全局假设β是不会变得),得到的回归参数估计将是回归参数在整个研究区域内的平均值,如上所说某一个因素在ABC等不同的地理位置对房价的影响是不同的,假如采用全局空间回归模型,便忽略了数据的空间位置属性,只反映平均意义下因变量与自变量的相关关系,而不能有效反映回归关系的空间非平稳性的特征。

如果两个变量之间的关系(可用回归系数表达)存在空间异质性,也就是在不同的地方有不同的回归系数,统计学将这种变量关系的空间异质性称之为空间非平稳性
所以地理加权回归应运而生,它考虑了空间关系的影响。
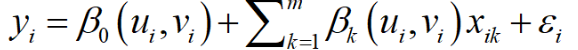
其中(ui,vi)为第i个采样点的坐标;βk(ui,vi)是第i个采样点上第k个回归参数,为空间地理位置函数,通过房价例子来看,加入地理位置函数可以反映房屋价格随地理位置的变化而变化的规律。
4. 加权篇
根据地理学第一定律,”所有事物之间都有关系,但是相近的事物关联更紧密“。
因为地理加权回归中的回归参数在每个数据采样点上都是不同的,所以不能直接利用参数回归方法估计其中的未知参数,我们需要对每个采样点都进行一个估计,有多少采样点就估计多少个β。100个点就估计100个β,β1-βn的估计便是加权最小二乘,这个权重便是W(u0, v0),为什么要考虑空间权重呢,它的作用就是衡量回归点要借用周围哪些样本点去进行估计,换句话说,空间权重决定了(如下图底部蓝色的圆圈)圈的大小。这个圈范围大了,那就变得与传统线性回归一样了,范围小了呢样本点太少就没有意义了。
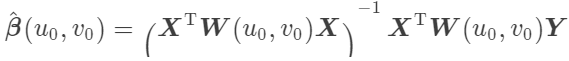
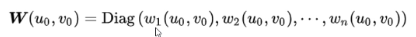
传统的线性回归估计是没有上式中W(u0, v0)这个空间权重矩阵的,所以没有考虑到距离对于采样点之间的相互影响,也就是没有体现地理学第一定律。
?
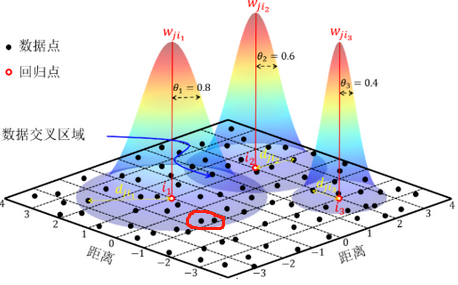
图中红圈的两个点本来就很近,假如被划分到两个不同的局部区域中,这样的话他们两个之间的相互影响关系都没有被考虑进去。图片来源是基于地理加权回归算法的中国台风设计风速区划图文章
所以根据数据所处空间位置,以不同数据点和回归点的空间距离为基础,对各数据点赋予不同的权重,离得近得样点在计算时候占的权重更大,离得远的样点占的权重小而后建立局部区域的加权回归方程。
根据地理学第一定律,GWR模型计算权重的基本原则为“距离越近,赋予的权重值越高;反之,权重值越低”。然后权重的具体计算(就是上图中的锥形),是通过关于空间距离的单调减函数实现,称之为核函数。有全局(Global)函数,距离阈值(Box-Car)函数,指数(Exponential)函数,高斯(Gaussian)函数,双重平方(Bi-square)函数(一般都是这两种),三次立方(Tri-cube)函数。
5. 带宽篇
带宽与核函数紧密相关。带宽(就是上图中的那个θ)变大,锥形就比较平缓,权重衰减的就慢,带宽变小,锥形就比较陡峭,权重衰减的很快。如何确定带宽下次再说啦。
水平有限,有些过程没有表达很清楚,特别是加权,如有错误欢迎指正和补充。
?
