Codes are available at https: //github.com/JUGGHM/OREPA_CVPR2022.
Abstract
Structural re-parameterization has drawn increasing attention in various computer vision tasks. It aims at improving the performance of deep models without introducing any inference-time cost. Though efficient during inference, such models rely heavily on the complicated training-time blocks to achieve high accuracy, leading to large extra training cost. In this paper, we present online convolutional reparameterization (OREPA), a two-stage pipeline, aiming to reduce the huge training overhead by squeezing the complex training-time block into a single convolution. To achieve this goal, we introduce a linear scaling layer for better optimizing the online blocks. Assisted with the reduced training cost, we also explore some more effective re-param components. Compared with the state-of-the-art re-param models, OREPA is able to save the training-time memory cost by about 70% and accelerate the training speed by around 2×. Meanwhile, equipped with OREPA, the models outperform previous methods on ImageNet by up to +0.6%. We also conduct experiments on object detection and semantic segmentation and show consistent improvements on the downstream tasks.
结构重参数化的目的是在不引入任何推理时间为代价的情况下提高深度模型的性能。
虽然这种模型在推理过程中效率很高,但它严重依赖于复杂的训练时间块来获得较高的精度,导致了大量的额外训练成本。
本文提出了一种两阶段的在线卷积重参数化 (OREPA) 方法,旨在通过将复杂的训练时间块压缩成单个卷积来减少巨大的训练开销。
为了实现这一目标,引入了一个线性缩放层,以更好地优化在线 blocks。在降低训练成本的同时,本文还探索了一些更有效的重新参数化组件。
与最先进的 re-param 模型相比,OREPA 能够节省约 70%的训练时间内存成本,训练速度提高约2倍。同时,配备了 OREPA 的模型在性能上比先前的工作也有所提升。
? Introduction??
精度与模型效率之间的权衡问题已被广泛讨论。一般来说,精度较高的模型通常需要更复杂的 blcok (complicated block),更宽或更深的结构。然而,这样的模型往往过于笨重,难以部署,尤其是在硬件性能有限、需要实时推断的情况下。考虑到效率,更小、更紧凑(compacter)和更快的模型是首选。
为了获得部署友好的模型(deploy-friendly model)并保持较高的精度,提出了基于结构重参数化的方法[14,16,17,19],以自由提高性能。在这些方法中,模型在训练阶段(training phase)和推理阶段(inference phase)具有不同的结构。具体来说,这些方法使用复杂的训练阶段拓扑(complicated training-phase topologies),即重新参数化的块(re-parameterized blocks),以提高性能。训练完成后,通过等效变换将复杂的块压缩成单一的线性层。压缩模型通常具有整洁的架构,例如,通常是类似 VGG 或类似 ResNet 的结构。从这个角度来看,重新参数化策略可以在不引入额外推理时间开销(inference-time cost)的情况下提高模型性能。
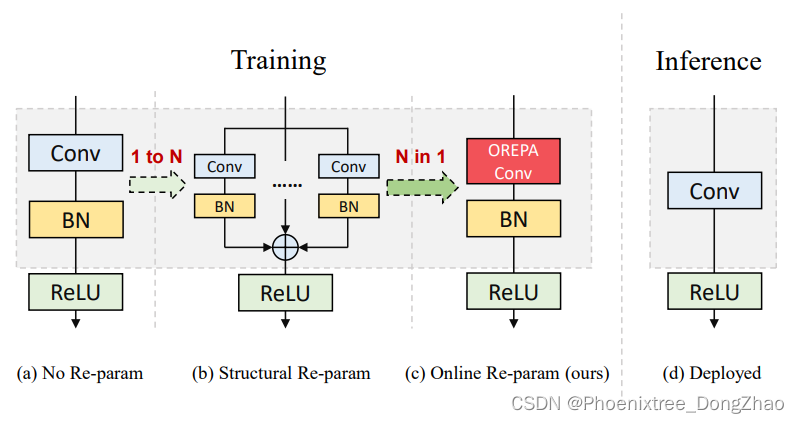
重新参数化普遍认为,归一化(范数)层(normalization (norm) layer)是重参数模型的关键组成部分。在重参数块 (图 1(b)) 中,总是在每个计算层之后添加一个范数层。可以观察到,去除这些规范层会导致严重的性能下降。然而,在考虑效率的同时,使用规范层却意外地给训练阶段带来了巨大的计算开销。在推理阶段,可以将复杂的数据块压缩成一个卷积层。但是,在训练过程中,范数层是非线性的,即它们以其标准差分割特征,这阻止了合并整个块。因此,存在大量的中间计算操作 (intermediate computational operations,大型 FLOPS) 和缓冲特性映射 (buffered feature maps,高内存使用)。更糟糕的是,高昂的训练预算(high training budget)使得探索更复杂和可能更强的重新参数块变得困难。自然,下面的问题就出现了
???? Why does normalization matter in re-param????
为什么规范化在重参数中很重要?
通过分析和实验,本文认为范数层中的比例因子(scaling factors)最重要(counts most),因为它们能够多样化不同分支的优化方向(diversify the optimization direction of different branches)。
?Figure 1. Comparison of (a) a vanilla convolutional layer, (b) a typical re-param block, and (c) our online re-param block in the training phase. All of these structures are converted to the same (d) inference-time structure.
基于观察结果,本文提出了在线重参数化 (Online Re-Parameterization, OREPA) (图 1 (c)),这是一个两阶段的 pipeline,能够简化复杂的训练时间重参数块(training-time re-param blocks)。
第一阶段,块线性化(block linearization),去除所有非线性范数层,并引入线性缩放层( linear scaling layers)。这些层具有与规范层类似的属性,它们多样化不同分支的优化(diversify the optimization of different branches)。此外,这些层是线性的,在训练时可以合并为卷积层。
第二阶段,块压缩(block squeezing),将复杂的线性块简化为单个卷积层。OREPA 通过减少中间计算层(intermediate computational layers)造成的计算和存储开销(computational and storage overhead),显著降低了训练成本(shrinks the training cost),而对性能的影响很小。此外,该算法的高效率使其可以探索更为复杂的重参数化拓扑(reparameterized topologies)。为了验证这一点,本文进一步提出了几个重新参数化的组件(re-parameterized components),以获得更好的性能。
? Online Re-Parameterization??
整体研究过程
首先,分析关键组成部分,即重参数化模型中的规范化层。在此基础上,提出了在线重参数化(OREPA) 方法,旨在大大减少重参数化模型的训练时间预算。OREPA 能够将复杂的训练时间块简化为单个卷积层,并保持较高的精度。OREPA 的总体流程如图 2 所示,包括?区块线性化阶段 和 区块挤压阶段。
接下来,通过分析多分支拓扑,更深入地探讨了重新参数化的有效性,并证明了所提出的线性缩放层和归一化层具有相似的效果。
最后,随着培训预算的减少,进一步探索了一些更强的重参数化的组件,略微增加了成本。
?Figure 2. An overview of the proposed Online Re-Parameterization (OREPA), a two-stage pipeline. In the first stage (Block Linearization), we remove all the non-linear components in the prototype re-param block. In the second stage (Block Squeezing), we merge the block to a single convolutional layer (OREPA Conv). Through the steps, we significantly reduce the training cost while keep the high performance.
1. 重参数化模型中的规范化层(Preliminaries: Normalization in Re-param)
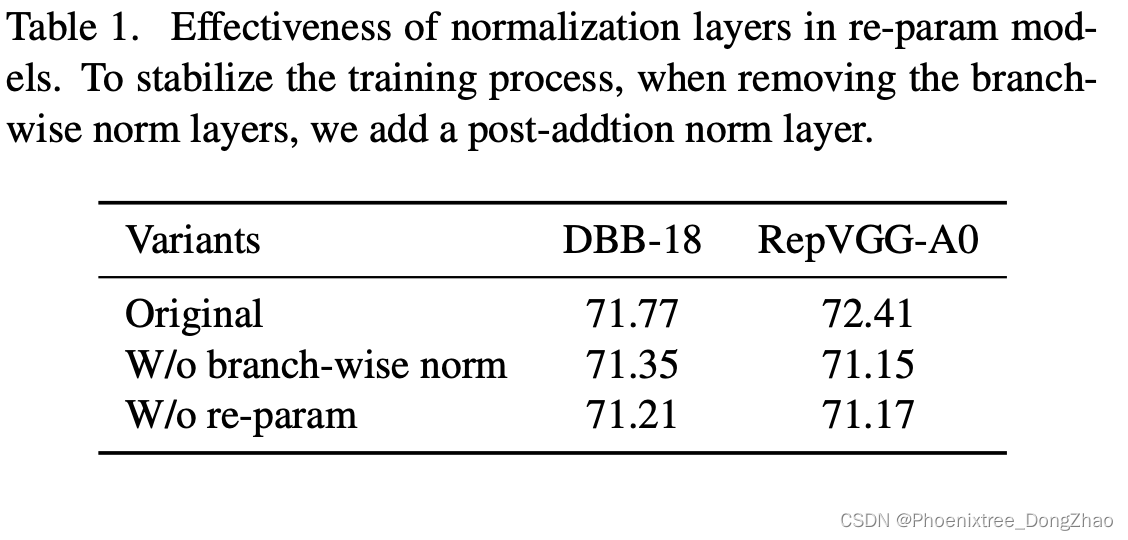
中间归一化层(intermediate normalization layers)是多分支结构再参数化的关键组成部分。以SoTA 模型 DBB[16]和 RepVGG[17] 为例,去除这些层会导致严重的性能下降(cause severe performance degradation),如表 1 所示。这一观测结果也得到了 Ding 等人的实验支持(experimentally supported) [16,17]。因此,认为中间规范化层对于重新参数化模型的性能至关重要。然而,中间规范层的使用意外地带来了更高的训练预算(unexpectedly brings higher training budgets)。注意到在推理阶段,重参数化块中的所有中间操作都是线性的,因此可以合并成(merged into)一个卷积层,从而得到一个简单的结构。但在训练过程中,范数层是非线性的,即它们将 feature map 除以其标准差。因此,中间操作需要单独计算,这会导致更高的计算和内存开销。更糟糕的是,如此高的成本将阻止社区探索更强大的训练模块(would prevent the community from exploring stronger training blocks)。
2. 区块线性化阶段 (Block Linearization)
中间规范化层阻止(prevent)在训练期间合并单独的层。然而,由于性能问题,直接删除它们并非易事(non-trivial)。为了解决这个难题(To tackle this dilemma),本文引入了基于通道的线性缩放操作(channel-wise linear scaling operation)作为归一化的线性替代(alternative of)。
缩放层包含一个可学习的向量,用于在通道维度上缩放特征图。线性伸缩层与规范化层具有相似的效果,它们都鼓励多分支向不同方向优化(be optimized towards diverse directions),这是重参数化中性能改进的关键。
除了对性能的影响,线性缩放层可以在训练期间合并,使在线重参数化成为可能。
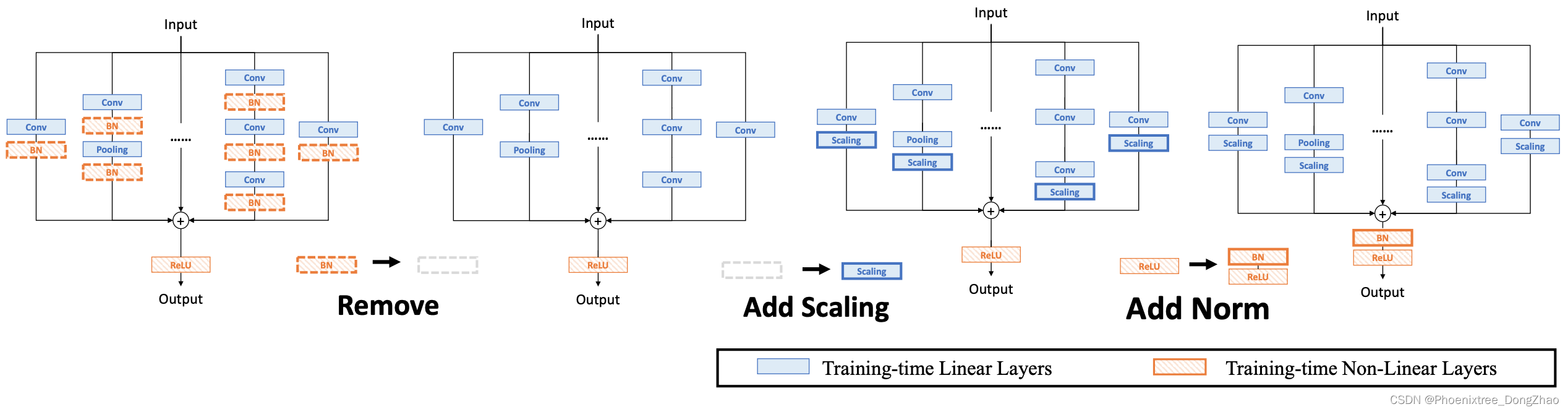
基于线性缩放层,本文对重参数化块进行修改,如图 3 所示。
具体来说,块线性化阶段包括以下三个步骤。
首先,去除所有非线性层,即重参数化块中的规范化层。
其次,为了保持优化多样性(maintain the optimization diversity),在每个分支的末端添加了一个尺度层,即归一化的线性选择。
最后,为了稳定训练过程,在添加所有分支之后添加一个后归一化层。一旦完成线性化阶段,在re-param 块中只存在线性层,这意味着可以在训练阶段合并块中的所有组件。
Figure 3. Three steps of block linearization. i) We first remove all the training-time non-linear normalization layers in the ra-param block. ii) Second, we add a linear scaling layer at the end of each branch to diversify the optimization directions. iii) Last, we add a post-normalization layer right after each block to stabilize training.
3. 区块挤压阶段 (Block Squeezing)
得益于块线性化(Benefiting from block linearization),得到了一个线性块。本节描述了将训练时间线性块压缩到单个卷积核中的标准程序。
块压缩步骤将在中间特征映射上的操作,这是计算和内存昂贵的(computation and memory expensive),转换为在内核上的操作,这是更经济的(economic)。这意味着在计算和内存方面都减少了从 O(H × W) 到 O(KH × KW) 的额外训练成本(extra training cost),其中 (H, W), (KH, KW) 是特征映射和卷积核的空间形状。
一般来说,无论线性重参数块有多复杂,以下两个属性始终有效。
? 区块中的所有线性层,例如,深度卷积,平均池化,以及前面提出的线性缩放,可以用一个退化的卷积层(degraded convolutional layer)表示,并具有相应的一组参数。
? 块可以由一系列并行分支表示,每个分支由一系列卷积层组成。
有了以上两个性质,如果能将 i) 一个多层 (即顺序结构) 和 ii) 一个多分支 (即并行结构) 简化为一个卷积,就可以挤压一个块。
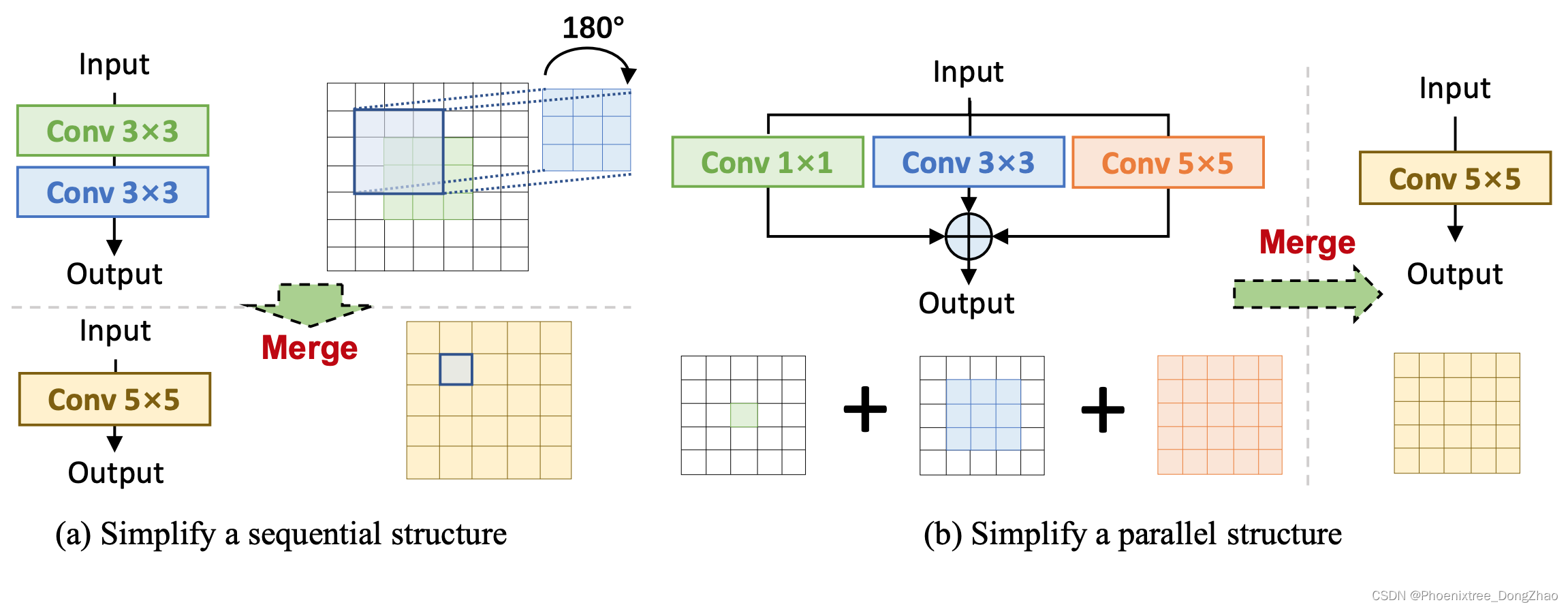
在接下来的部分,将展示如何简化顺序结构 (图4(a)) 和并行结构 (图4(b))。
Figure 4. Simplification of sequential and parallel structures. Such simplifications convert the heavy computations on the feature maps to the lighter ones on the convolutional kernels.?
定义卷积的符号:令 Ci, Co 表示 K_H × K_W 大小的二维卷积核的输入和输出通道数。
X∈R^{Ci×H×W}, Y∈R^{Co×H ' ×W '} 表示输入和输出张量。
省略了这里的偏差,卷积过程用 ? (式1)表示。
简化顺序结构
考虑一个由??表示的卷积层堆栈(a stack of),其中Wj∈R^{Cj×Cj?1×KHj×KWj} 满足 C0 = Ci, CN = Co。
根据结合律 (the associative law),这些层可以按照下式挤进 (be squeezed into) 一个卷积内核:
Wj 表示第 j 层的重量。
简化并行结构
并行结构的简化是微不足道的(trivial)。根据卷积的线性特性,可以根据下式多个分支合并到一个:
Wm 是 m 分支的重量,??是统一的重量。
值得注意的是,当合并不同大小的内核时,需要对齐不同内核的空间中心,例如,1×1 内核应该与3×3 内核的中心对齐。
训练开销:从特征到内核
无论块有多复杂,它必须由不超过多分支和多层的子拓扑组成。因此,根据上述两种化简规则,可以将其简化为单个化简。最后,可以得到一体化的端到端映射权值,并且在训练过程中只进行一次卷积。
实际可以将中间特征映射上的运算 (卷积、加法) 转换为卷积核上的运算。因此,将重参数块的额外训练成本从 O(H × W) 降低到 O(K_H × K_W)。
‘
4. 多分支拓扑(Gradient Analysis on Multi-branch Topology)
为了理解为什么块线性化步骤是可行的,即为什么缩放层是重要的,我们对统一权重重参数化的优化进行了分析。
结论是,对于去除规范层的分支,利用伸缩层可以使其优化方向多样化,并防止其退化为单一的。
证明过程可以参考原文(我也没读,用到的时候再研究吧)。
5. 更强的重参数化的组件(Block Design)
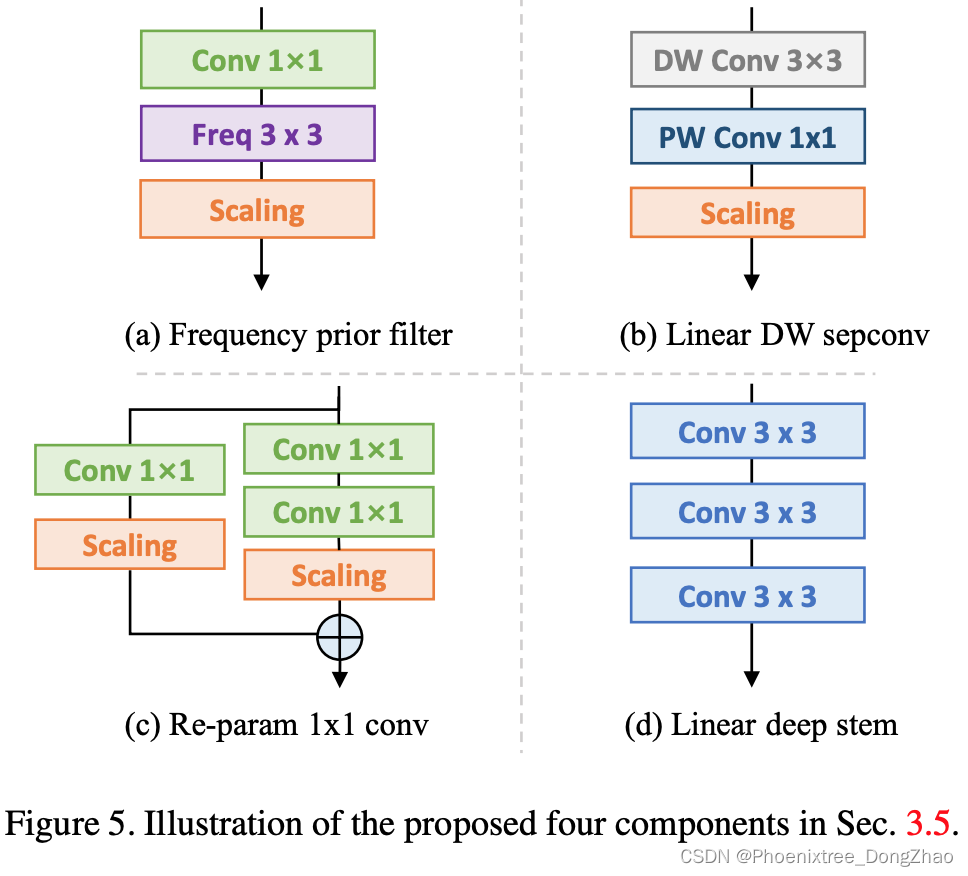
由于提出的 OREPA 大大节省了训练成本,它能够允许我们探索更复杂的训练块。因此,通过线性化最先进的模型 DBB[16],并插入以下组件?(图5),设计了一种新的重参数化模型,即 OREPA-ResNet。
Frequency prior filter
在前面的工作[16]中,在块中使用池层。Qin et al.[31] 认为池化层是频率滤波器的一种特殊情况。为此,本文添加了一个 Conv1×1 - Frequency Filter 分支。
Linear depthwise separable convolution
本文稍微修改了深度可分卷积[10],去掉了中间的非线性激活层,使其在训练时可以合并。
Re-parameterization for 1×1 convolution
以前的工作主要集中在 3×3 卷积层的重参数,而忽略了1×1 层。本文建议重新参数化 1×1 层,因为它们在瓶颈结构中发挥着重要作用[21,4]。具体来说,添加了一个额外的 Conv1×1 - Conv1×1 分支。
Linear deep stem
大型卷积核通常被放置在最开始的层,例如 7×7 stem 层[21],目的是获得更大的接收野。Guo 等人将 7×7 conv 层替换为堆叠的 3×3 层,以获得更高的精度[19]。然而,由于高分辨率,堆叠在最开始层的卷积需要更大的计算开销。值得注意的是,可以用本文提出的线性缩放层挤压堆叠的deep stem 至 7×7 conv 层,可以大大降低训练成本,同时保持较高的精度。
?
对于 OREPA-ResNet 中的每个块 (图6):
i),添加一个频率先验滤波器(Frequency prior filter)和一个线性深度可分离卷积。
ii) 将所有 stem 层 (即初始的 7×7 卷积) 替换为提出的线性 deep stem。
iii) 在瓶颈[21]块中,除了 i) 和 ii),还将原来的 1×1?卷积分支替换为提议的 Rep-1×1 块。
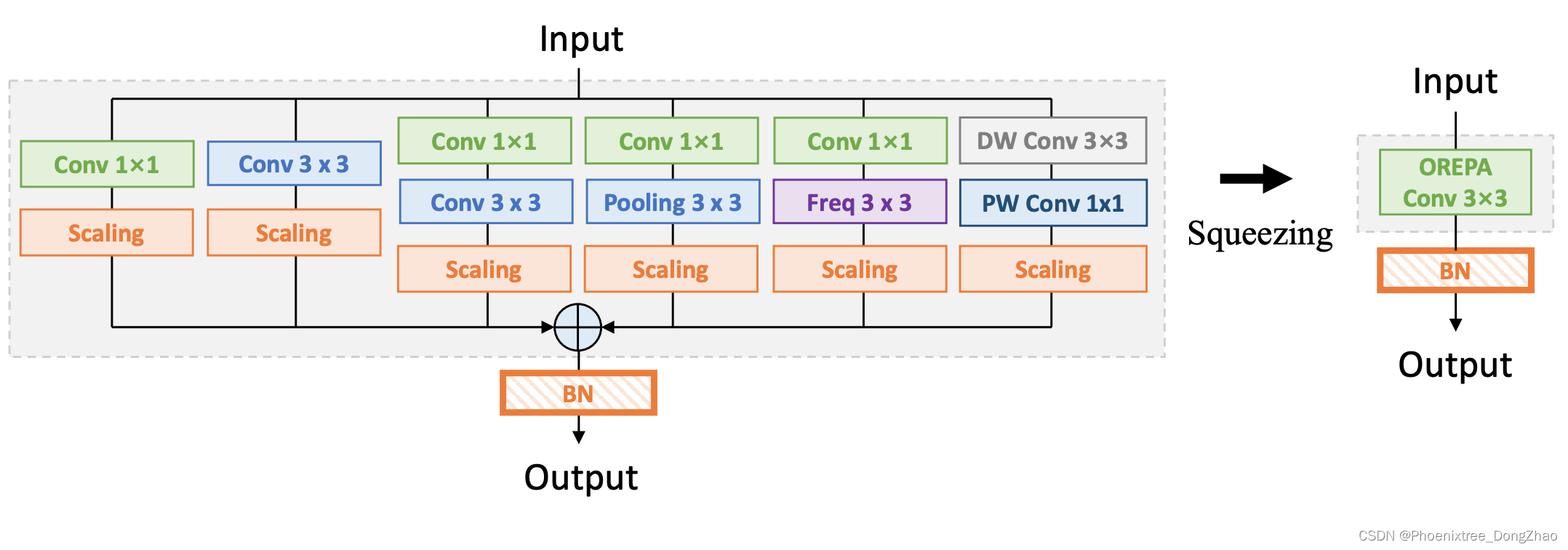
Figure 6. The design of the proposed OREPA block, corresponding to a 3×3 convolution during training and inference.?
-----------------------------
结构重参数化
结构重参数化近年来受到越来越多的重视,并应用于许多计算机视觉任务,如紧凑模型设计 [18],体系结构搜索 [9,43] 和剪枝 [15]。重新参数化是指通过参数的等效变换,可以将不同的体系结构相互转换。例如,1x1 卷积的一个分支和 3x3 卷积的一个分支,可以转换成 3x3 卷积的一个分支[17]。在训练阶段,多分支 [14,16,17] 和多层 [19,5] 拓扑被设计用来替代传统的线性层 (如 conv 或全连接层[1]) 用于增强模型。Cao 等人 [5] 在训练中讨论了如何合并深度可分卷积核。在推理过程中,将训练时间较长的复杂模型转换为简单模型,以提高推理速度。虽然受益于复杂的训练时间拓扑,目前的重新参数化方法 [14,16,19] 的训练需要不可忽略的额外计算成本。当块为了更强的表示而变得更复杂时,GPU 的内存利用率和用于训练的时间会变得越来越大,最终达到不可接受的程度。与以往的 re-param 方法不同,本文更注重训练成本。本文提出了一种通用的在线卷积重参数化策略,使训练时间结构重参数化成为可能。