文章目录
一. 图像直方图
① 什么是图像直方图
加入图像是灰度图像,则其直方图就是灰度级的函数,描述的是每种灰度级像素的个数,反应到图像上就是每种灰度出现的频率.横坐标是灰度级,纵坐标是出现的频率(对于图形来说,就是这个灰度级在图像中出现的次数)

非归一化的直方图数学表达:

其中rk为图像的灰度值,比如常见的是0~255之间的某个值,nk为图像中灰度级为rk的像素的个数.
归一化的直方图
什么叫归一化,就是把灰度出现的次数换算成0~1之间,其实从另外一个角度来说,归一化之后,就变成了灰度级的密度分布,就是某个灰度级在图像中出现的概率.

其中MN就是像素的总数,M和N表示图像的行数和列数
② 灰度图像的直方图的绘制
计算直方图
函数原型:
1)void cv::calcHist(const Mat *images,
int nimages,
const int* channels,
InputArray mask,
OutputArray hist,
int dims,
const int* histSize,
const float* ranges,
bool uniform = true,
bool accumulate =false)
2)void cv::calcHist(const Mat *images,
int nimages,
const int* channels,
InputArray mask,
SparseMat& hist,
int dims,
const int* histSize,
const float* ranges,
bool uniform = true,
bool accumulate =false)
3)void cv::calcHist(InputArrayOfArrays Images,
const std::vector<int>& channels,
InputArray mask,
OutputArray hist,
const std::vector<int>& histSize,
const std::vector<int>& ranges,
bool accumulate = false)
参数说明:
images:表示图像列表,这些图像必须具有相同的深度信息CV_8U,CV_16U或者CV_32F,并且这些图像的大小相同,这些图像可以有任意的通道数量.nimages:表示输入图像的图像个数channels:表示的是通道索引列表.0,1,2来表示.怎么理解这个参数,下面会解释mask:可选掩码,如果图像不为空,则此参数必须为8位和图像大小相同,掩码中的非零元素标记需要再直方图中统计的数据元素hist:输出计算得到的直方图,是一个密集或者稀疏矩阵dims:输出的直方图的维度,灰度为1,彩色为3.histSize:直方图横坐标的区间数,就是直方图横坐标的范围ranges:统计像素值的区间,范围如0~255表示统计0到255的数组uniform:是否进行均匀统计,也就是说每个竖条的高度是否相等.accumulate:多个图像时,是否累计计算像素值的个数.
channels:参数的理解:
直方图的统计都是针对单通道图片的额,所以如果出现了多通道的图片,那就对其单个铜套分别依次统计,如果是多幅图片,那就把所有图片的通道按顺序编号(从0开始),然后channels就存储相应的通道序号即可.
现在说单幅图片的,如果只有一张图片,则你要同时统计BGR通道的,这个时候你传入的channels = {0,1,2},如果你只要统计一个通道的,你可以直接channels = {0} 或者 {1} 或者 {2}
再比如你有两幅图片img1(三通道),img2(单通道)
则channels = {0,1,2,0} 相当于是先统计图像1的三个通道分别统计,然后img2只统计单通道的.
还有一个模棱两可的说法就是那个ranges的区间问题,如果设置为(0,255),就统计不到255像素的值,我们来写个例子验证一下.
#include"MyOpencv.h"
int main(void)
{
Mat imageSrc = Mat::zeros(Size(3, 3), CV_8UC1);
imageSrc.at<uchar>(0, 0) = 255;
imageSrc.at<uchar>(0, 1) = 255;
imageSrc.at<uchar>(0, 2) = 128;
imageSrc.at<uchar>(1, 0) = 128;
imageSrc.at<uchar>(1, 1) = 128;
imageSrc.at<uchar>(1, 2) = 255;
const int channels[] = {0}; // 第0幅图的第0个通道
Mat hist;
int dims = 1; // 设置直方图的维度
const int histSize[] = { 256 }; // bin的个数,就是竖条的个数
float pranges[] = { 0,255 }; // 取值区间,这里到底包不包括255
const float *ranges[] = { pranges };
calcHist(&imageSrc, 1, channels, Mat(), hist, dims, histSize, ranges, true,false);
cout << hist.at<float>(0) << endl;
cout << hist.at<float>(128) << endl;
cout << hist.at<float>(255) << endl;
imshow("Original", imageSrc);
waitKey(0);
return 0;
}
结果是:

所以那里的pranges = {a,b} 是一个前闭后开的区间,应该写成 {0,256},换成{0,256}之后的结果:

绘制一个灰度图的直方图:
#include "MyOpencv.h"
int main(void)
{
Mat imageSrc = imread("test_11.bmp", IMREAD_GRAYSCALE);
if (imageSrc.empty())
{
cout << "图像出错,图像不存在!" << endl;
return -1;
}
imshow("Original", imageSrc);
// 获取灰度图像直方图
int histSize = 256;
float ranges[] = { 0,256 };
const float *histRanges = { ranges };
int channels[1] = { 0 };
Mat hist;
calcHist(&imageSrc, 1, channels, Mat(), hist, 1, &histSize, &histRanges, true, false);
// 创建直方图显示图像
int histH = 300;
int histW = 512;
int binW = histW / histSize;
Mat histImage(histH, histW, CV_8UC3, Scalar(0, 0, 0));
normalize(hist, hist, 0, histH, NORM_MINMAX, -1, Mat());
for (int i = 1; i < histSize; i++)
{
line(histImage, Point((i - 1) * binW, histH - cvRound(hist.at<float>(i - 1))),
Point((i)*binW, histH - cvRound(hist.at<float>(i))), Scalar(255, 0, 0), 2, 8, 0);
}
imshow("histImage", histImage);
waitKey(0);
return 0;
}
结果:

normalize 归一化函数讲解:
void normalize( InputArray src, InputOutputArray dst, double alpha = 1, double beta = 0,
int norm_type = NORM_L2, int dtype = -1, InputArray mask = noArray());
该函数归一化输入数组使得它的范数或者是数值范围在一定的范围内.
参数解释:
-
src:输入数组 -
dst:输出数组,支持原地运算 -
alpha:归一化的数据的最小值 -
beta:归一化数据的最大值,不用于范数归一化模式 -
normType: 归一化的类型NORM_MINMAX:数组的数值被平移或者缩放到一个指定的范围,线性归一化,一般比较常用NORM_INF:无穷范数NORM_L1:归一化数组L1-范数(绝对值的和)NORM_L2:归一化数组的(欧几里德)L2-范数
-
dtype:为负数时,输出数据类型和输入数据类型一致,否则和src通道数一致,depth = CV_MAT_DEPTH(dtype)define CV_CN_SHIFT 3 #define CV_DEPTH_MAX (1 << CV_CN_SHIFT) #define CV_MAT_DEPTH_MASK (CV_DEPTH_MAX - 1) #define CV_MAT_DEPTH(flags) ((flags) & CV_MAT_DEPTH_MASK)
到底是个啥,我也没搞清楚
mask:掩膜,用于指示函数是否仅仅对指定的元素进行操作
归一化的公式:
线性转换之下: NORM_MINMAX
简单的解释就是计算在之前的范围内的跨度,也就是比重,然后把它落到新的区间内,根据比重计算跨度,然后再加上新区间的初始位置.
dst(i,j) = [src(i,j) - min(src)] / (max(src) - min(src)) * (maxNew - minNew) + minNew
其中maxNew = 设置的参数beta,minNew = 设置的参数alpha
③ 彩色图像的直方图的绘制
#include "MyOpencv.h"
int main(void)
{
Mat imageSrc = imread("test_12.bmp", IMREAD_COLOR);
imshow("Original", imageSrc);
// 通过channels来控制直方图
int histSize = 256;
float range[] = { 0,256 };
const float *histRange = { range };
Mat bHist, gHist, rHist;
int numbins = 256;
int channels[1] = { 0 };
int dimsOut = 1;
calcHist(&imageSrc, 1, channels, Mat(), bHist, dimsOut, &histSize, &histRange, true, false);
channels[0] = 1;
calcHist(&imageSrc, 1, channels, Mat(), gHist, dimsOut, &histSize, &histRange, true, false);
channels[0] = 2;
calcHist(&imageSrc, 1, channels, Mat(), rHist, dimsOut, &histSize, &histRange, true, false);
int width = 512;
int height = 300;
Mat histImage(Size(width, height), CV_8UC3, Scalar(20, 20, 20));
// 归一化处理
normalize(bHist, bHist, 0, height, NORM_MINMAX);
normalize(gHist, gHist, 0, height, NORM_MINMAX);
normalize(rHist, rHist, 0, height, NORM_MINMAX);
// 计算每个像素的刻度值
int binStep = cvRound(float(width) / float(numbins));
for (int i = 1; i < numbins; i++)
{
line(histImage, Point(binStep * (i - 1), height - cvRound(bHist.at<float>(i - 1))),
Point(binStep * (i), height - cvRound(bHist.at<float>(i))),
Scalar(255, 0, 0));
line(histImage, Point(binStep * (i - 1), height - cvRound(gHist.at<float>(i - 1))),
Point(binStep * (i), height - cvRound(gHist.at<float>(i))),
Scalar(0, 255, 0));
line(histImage, Point(binStep * (i - 1), height - cvRound(rHist.at<float>(i - 1))),
Point(binStep * (i), height - cvRound(rHist.at<float>(i))),
Scalar(0, 0, 255));
}
imshow("BgrHist", histImage);
waitKey(0);
return 0;
}
结果:

二. 直方图均衡化
① 直方图均衡化原理详解
直方图均衡化的作用是图像增强,它的原理是如下的:
设输入图像为二元函数f(x,y),输出图像为二元函数g(x,y),一般来说,灰度值分布比较平均的图像,通常对比度都比较高.比如下图:
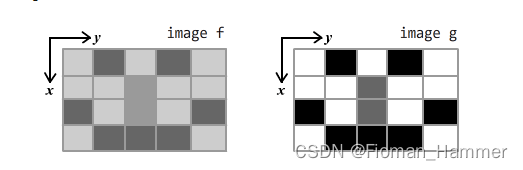
那么如何做才能实现均衡化呢? 先说一下直方图均衡化的目标
让均衡化的图像大致的像素出现次数大致的满足一种均匀分布,具体是怎么做的呢?
分成两步:
- 第一是使用累计概率密度,计算出来累计的概率密度
- 让累计的概率密度乘以像素范围即可得到当前像素级的均衡化的像素值
累计概率密度计算公式:
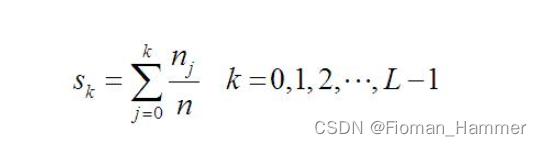
n是图像的像素数的总和,nj是当前的灰度级的像素的个数.L是图像中可能的灰度级总数,一般常用的是256.
好多资料到这里就完了,但是其实上面只是计算除了它的均衡化之后的概率密度,最后还要乘以(L-1),才是最终的均衡化的结果
dst(val) = sk * (L - 1) = sk * 255(一般图像的灰度级都是256)
例如一个4*4的图像:

经过公式计算得到:

写程序验证一下:
#include "MyOpencv.h"
int main(void)
{
Mat original = Mat::ones(Size(4, 4), CV_8UC1) * 255;
original.at<uchar>(0, 1) = 128;
original.at<uchar>(0, 2) = 200;
original.at<uchar>(0, 3) = 50;
original.at<uchar>(1, 0) = 50;
original.at<uchar>(1, 1) = 200;
original.at<uchar>(1, 3) = 50;
original.at<uchar>(2, 1) = 200;
original.at<uchar>(2, 2) = 128;
original.at<uchar>(2, 3) = 128;
original.at<uchar>(3, 0) = 200;
original.at<uchar>(3, 1) = 200;
original.at<uchar>(3, 3) = 50;
cout << "Original = " << endl;
cout << original << endl;
Mat dst;
equalizeHist(original, dst);
cout << "dst = " << endl;
cout << dst << endl;
return 0;
}
结果:

结果好像跟我们预测的不太一样,为什么呢? 原来在直方图均衡化的操作的时候,如果图像太小,会有特殊的处理.源码看的不是很明白,最终的计算方式肯定就是这样的
② 直方图均衡化案例:

代码示例:
#include "MyOpencv.h"
void draw_hist(Mat &hist, int type, string name)
{
// 归一化并且绘制直方图
int histWith = 512;
int histHeight = 400;
int step = 2;
Mat histImage = Mat::zeros(Size(histWith, histHeight), CV_8UC3);
normalize(hist, hist,0,histHeight,type,-1,Mat());
for (int i = 1; i < hist.rows; i++)
{
line(histImage, Point(step * (i - 1), cvRound(histHeight - hist.at<float>(i - 1))),
Point(step * i, cvRound(histHeight - hist.at<float>(i))),
Scalar(255, 255, 255));
}
imshow(name, histImage);
}
int main(void)
{
Mat imageSrc = imread("test_14.bmp", IMREAD_GRAYSCALE);
imshow("Original", imageSrc);
Mat dst;
equalizeHist(imageSrc, dst);
imshow("EqualizeRes", dst);
// 计算直方图并且绘制直方图
const int channels[1] = { 0 };
float inRanges[2] = { 0,256 };
const int dimOut = 1;
int histSize = 256;
const float *ranges = { inRanges };
Mat hist1, hist2;
calcHist(&imageSrc, 1, channels, Mat(), hist1, dimOut, &histSize, &ranges);
calcHist(&dst, 1, channels, Mat(), hist2, dimOut, &histSize, &ranges);
draw_hist(hist1, NORM_MINMAX, "hist_01");
draw_hist(hist2, NORM_MINMAX, "hist_02");
waitKey(0);
return 0;
}
结果:
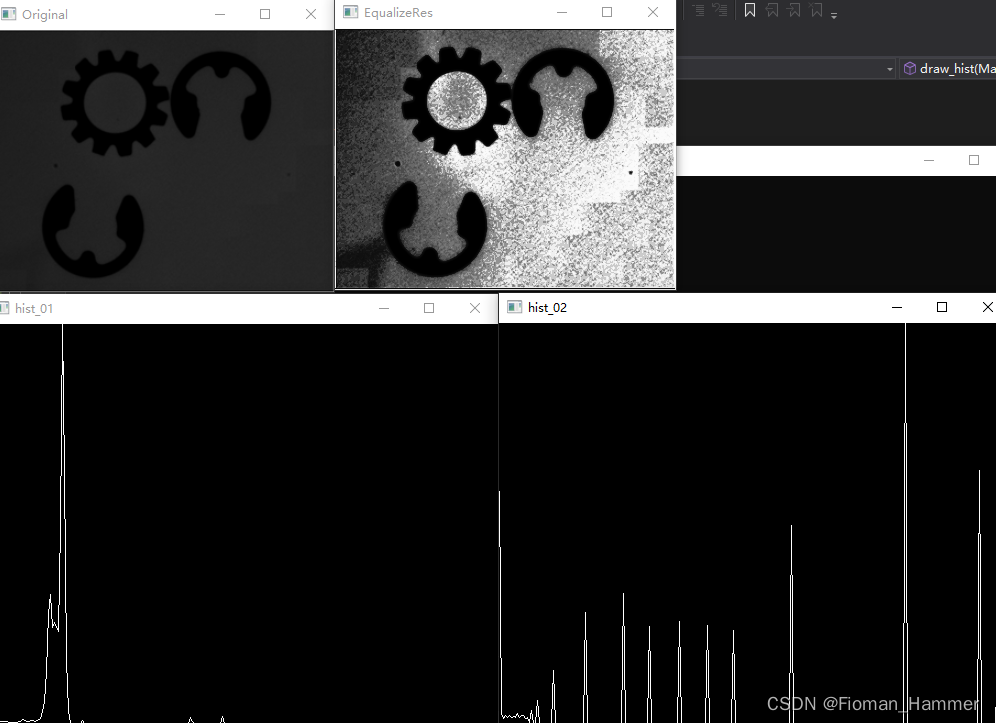
三. 直方图匹配
① 直方图匹配的原理
直方图匹配和直方图的均衡化类似,都是对直方图的分部形式进行更改.只是直方图的均衡化的目的是把直方图改成均匀分部的形式,而直方图的匹配(直方图规定化)后的直方图是可以随意指定的,即在执行直方图匹配操作的时候,首先要找到变换后的灰度直方图分布形式,进而确定变换函数.直方图匹配操作能够有目的的增强某个灰度区间,相比于直方图均衡化操作,该算法虽然多了一个输入,但是其变换后的结果也更具有灵活性.
由于不同的图像的像素数目不同,为了使两个图像直方图能够匹配,需要使用概率形式去表示每个灰度值在图像上的所占用的比例.理想状态下,经过图像直方图匹配操作后图像直方图分布形式应该与目标分布一致,因此两者之间的累计概率分布也是一致的.累计概率为小于等于某一灰度值的像素数目占所有像素的比例.我们使用Vs表示原图像直方图的各个灰度级的累计概率,用Vs表示匹配后直方图的各个灰度级累计概率.那么确定由原图像中灰度值n映射成r的条件如式:

为了更清楚的说明直方图的匹配过程,下图给出了一个示例:

示例中目标直方图灰度值为2以下的概率都是0,灰度值3的累积概率为0.16,灰度值4的累积概率为0.35,原图像直方图灰度值为0时概率为0.19.0.19距离0.16的距离小于距离0.25的距离,因此需要将原图像中灰度值0匹配成灰度值3.同样,原图像灰度值1的累积概率为0.43,其距离目标直方图灰度值4的累积概率0.35的距离为0.08,二距离目标直方图灰度值5的累积概率0.64的距离为0.21,因此需要将原图像中灰度值1匹配成灰度值4.
这个寻找灰度值匹配的过程是直方图匹配算法的关键,在代码实现中我们可以通过构建原直方图累积概率与目标直方图累积概率之间的差值表,寻找原直方图中灰度值n的累积概率与目标直方图中所有灰度值累积概率差值的最小值,这个最小值对应的灰度值r就是n匹配后的灰度值.
② 直方图匹配的实现
#include "MyOpencv.h"
void draw_hist(Mat &hist, int type, string name)
{
// 归一化并且绘制直方图
int histWith = 512;
int histHeight = 400;
int step = 2;
Mat histImage = Mat::zeros(Size(histWith, histHeight), CV_8UC3);
normalize(hist, hist, 1, 0, type, -1, Mat());
for (int i = 1; i < hist.rows; i++)
{
rectangle(histImage, Point(step * (i - 1), histHeight - 1),
Point(step * i - 1, histHeight - cvRound(20 * histHeight * hist.at<float>(i - 1)) - 1),
Scalar(255, 255, 255), -1);
}
imshow(name, histImage);
}
int main(void)
{
Mat img1 = imread("test_18.bmp", IMREAD_GRAYSCALE);
Mat img2 = imread("test_19.bmp", IMREAD_GRAYSCALE);
Mat hist1, hist2;
const int channels[1] = { 0 };
float inRanges[2] = { 0,256 };
const float *ranges = { inRanges };
int histSize = 256;
int dimsOut = 1;
calcHist(&img1, 1, channels, Mat(), hist1, dimsOut, &histSize, &ranges);
calcHist(&img2, 1, channels, Mat(), hist2, dimsOut, &histSize, &ranges);
// 归一化两张图像
draw_hist(hist1, NORM_INF, "HIST_01");
draw_hist(hist2, NORM_INF, "HIST_02");
// 计算两张图的直方图的累积概率
float hist1CDF[256] = { hist1.at<float>(0) };
float hist2CDF[256] = { hist2.at<float>(0) };
for (int i = 1 ;i < 256; i++)
{
hist1CDF[i] = hist1CDF[i - 1] + hist1.at<float>(i);
hist2CDF[i] = hist2CDF[i - 1] + hist2.at<float>(i);
}
// 构建累积概率误差矩阵
float diffCDF[256][256];
for (int i = 0; i < 256; i++)
{
for (int j = 0; j < 256; j++)
{
diffCDF[i][j] = fabs(hist1CDF[i] - hist2CDF[j]);
}
}
// 生成LUT映射表
Mat lut(1, 256, CV_8U);
for (int i = 0; i < 256; i++)
{
// 查找源灰度级为i的映射灰度
// 和i的劣迹概率差值最小的规定化灰度
float min = diffCDF[i][0];
int index = 0;
for (int j = 1; j < 256; j++)
{
if (min > diffCDF[i][j])
{
min = diffCDF[i][j];
index = j;
}
}
lut.at<uchar>(i) = (uchar)index;
}
Mat result, hist3;
LUT(img1, lut, result);
imshow("待匹配的图像", img1);
imshow("匹配的模板图像", img2);
imshow("直方图匹配结果", result);
calcHist(&result, 1, channels, Mat(), hist3, dimsOut, &histSize, &ranges);
draw_hist(hist3, NORM_MINMAX, "hist3");
waitKey(0);
return 0;
}
结果:

