在生物神经网络中，每个神经元与其他神经元相连，当它“兴奋”时，就会向相连的神经元发送化学物质，从而改变这些神经元内的电位；如果某神经元的电位超过了一个“阈值”，那么它就会被激活，即“兴奋”起来，向其他神经元发送化学物质。

1943 年，McCulloch 和 Pitts 将上述情形抽象为上图所示的简单模型，这就是一直沿用至今的 M-P 神经元模型。把许多这样的神经元按一定的层次结构连接起来，就得到了神经网络。

?一个简单的神经元如下图所示：

1.2 单层神经网络

单层神经网络是最基本的神经元网络形式，由有限个神经元构成，所有神经元的输入向量都是同一个向量。由于每一个神经元都会产生一个标量结果，所以单层神经元的输出是一个向量，向量的维数等于神经元的数目。

示意图如下：

1.3 感知机

感知机由两层神经网络组成，输入层接收外界输入信号后传递给输出层（输出+1正例，-1反例），输出层是 M-P 神经元。

感知机的作用：

把一个n维向量空间用一个超平面分割成两部分，给定一个输入向量，超平面可以判断出这个向量位于超平面的哪一边，得到输入时正类或者是反类，对应到2维空间就是一条直线把一个平面分为两个部分

1.4 多层神经网络

多层神经网络就是由单层神经网络进行叠加之后得到的，所以就形成了层的概念，常见的多层神经网络有如下结构：

输入层（Input layer），众多神经元（Neuron）接受大量输入消息。输入的消息称为输入向量。

输出层（Output layer），消息在神经元链接中传输、分析、权衡，形成输出结果。输出的消息称为输出向量。

隐藏层（Hidden layer），简称“隐层”，是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有一层或多层。隐层的节点（神经元）数目不定，但数目越多神经网络的非线性越显著，从而神经网络的强健性（robustness）更显著。

示意图如下：

概念：全连接层

全连接层：当前一层和前一层每个神经元相互链接，我们称当前这一层为全连接层。

思考：假设第N-1层有m个神经元，第N层有n个神经元，当第N层是全连接层的时候，则N-1和N层之间有多少个参数w，这些参数可以如何表示？

从上图可以看出，所谓的全连接层就是在前一层的输出的基础上进行一次Y=Wx+b的变化(不考虑激活函数的情况下就是一次线性变化，所谓线性变化就是平移(+b)和缩放的组合(*w))

1.5 激活函数

在前面的神经元的介绍过程中我们提到了激活函数，那么他到底是干什么的呢？

假设我们有这样一组数据，三角形和四边形，需要把他们分为两类

通过不带激活函数的感知机模型我们可以划出一条线, 把平面分割开

假设我们确定了参数w和b之后，那么带入需要预测的数据，如果y>0,我们认为这个点在直线的右边，也就是正类（三角形），否则是在左边（四边形）。

但是可以看出，三角形和四边形是没有办法通过直线分开的，那么这个时候该怎么办？

可以考虑使用多层神经网络来进行尝试，比如在前面的感知机模型中再增加一层

?

?对上图中的等式进行合并，我们可以得到：

上式括号中的都为w参数，和公式y = w_1x_1 + w_2x_2 +b完全相同，依然只能够绘制出直线。所以可以发现，即使是多层神经网络，相比于前面的感知机，没有任何的改进。

但是如果此时，我们在前面感知机的基础上加上非线性的激活函数之后，输出的结果就不在是一条直线。

如上图，右边是sigmoid函数，对感知机的结果，通过sigmoid函数进行处理

如果给定合适的参数w和b，就可以得到合适的曲线，能够完成对最开始问题的非线性分割

所以激活函数很重要的一个作用就是增加模型的非线性分割能力

常见的激活函数有：

看图可知：

sigmoid 只会输出正数，以及靠近0的输出变化率最大

tanh和sigmoid不同的是，tanh输出可以是负数

Relu是输入只能大于0,如果你输入含有负数，Relu就不适合，如果你的输入是图片格式，Relu就挺常用的，因为图片的像素值作为输入时取值为[0,255]。

激活函数的作用除了前面说的增加模型的非线性分割能力外，还有

提高模型鲁棒性

缓解梯度消失问题

加速模型收敛等

2 深度学习三部曲

不管多么复杂的网络都包含这三步骤:正向传播、反向传播、梯度下降

2.1 正向传播

?正向传播过程：x1,x2,x3经过运算传递到下一层A11,A12,A13,A14,再经过运算传递到下一层，直到传递到输出层A31。y_hat是A31的拷贝。

解释：全连接网络后一层神经元会链接上一层所有神经元，上面图并没有体现出来，一是为了简便，二是因为在实际传播过程中，可以人为控制传递哪些神经元。

正向传播细节：

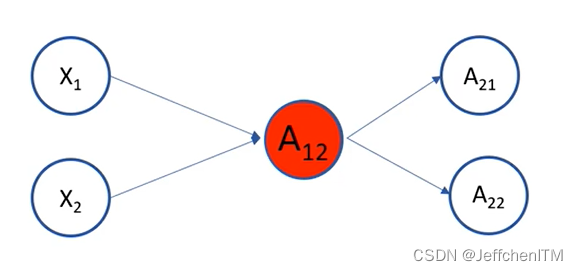
?以A12为例

? ? ? ? 输入：X1 ,? X2

? ? ? ? 输出：只有一个值，但把这个值传递给了2个神经元

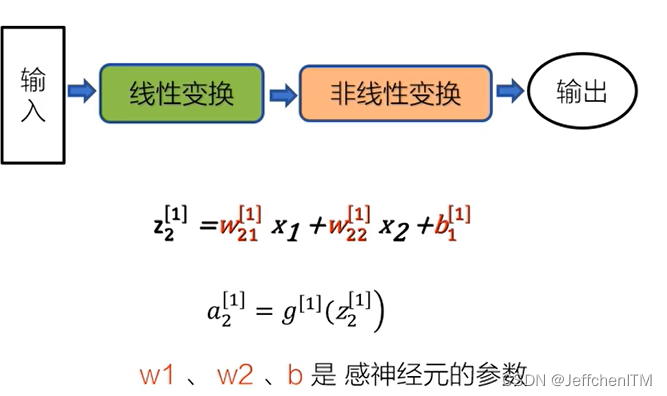
?内部运算包含2个部分：线性变换和非线性变换

?值得注意的是在正向传播的时候，w和b是已知值，所谓训练模型就是找到合适的参数值。

2.2 反向传播

在正向传播过程中，w和b被视为已知量
在反向传播过程中，w和b被视为未知量

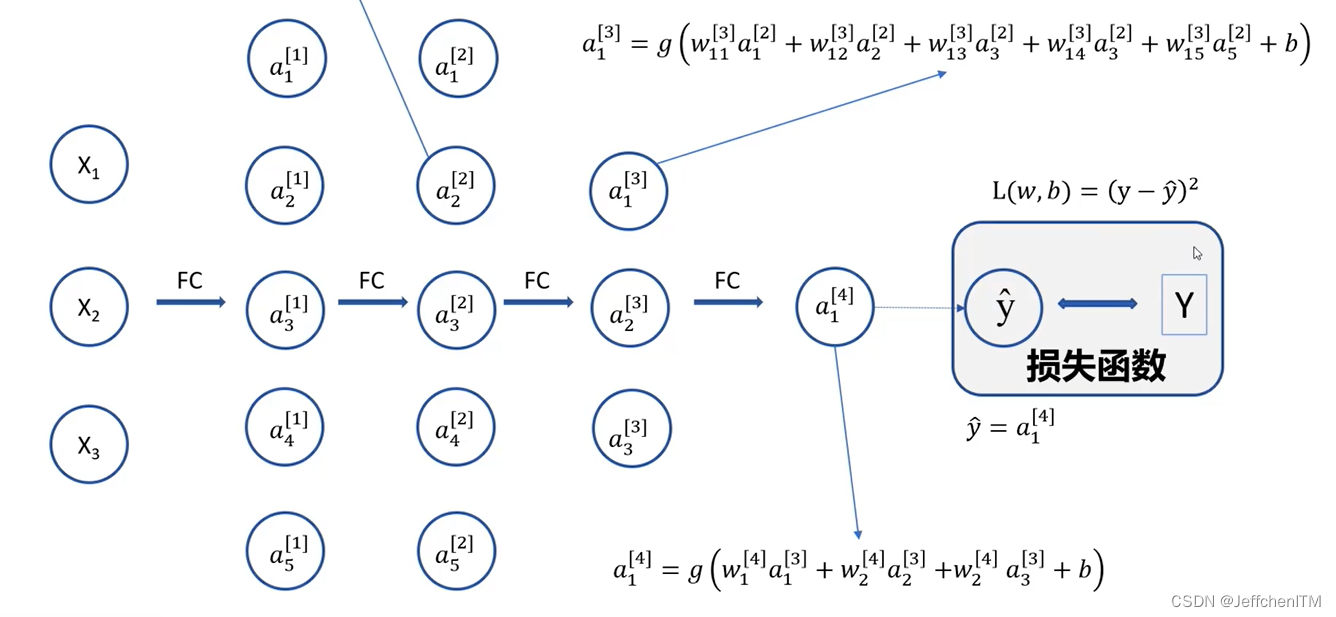
?如上图所示，每一层的输出都可以通过层层嵌套最终表示成 w和b的关系式，为下面反向传播做准备。

?以第二层a2（上图正方形框住的神经元）为例，L是损失函数表达式，我们要求该处的偏导值，第一步需要先求L对a2的偏导，需要通过第三层的三个神经元，具体公示如下：

通过该公式我们可以求得?L对a2的偏导值，接着再去求L对w和b的偏导值，公式如下：

?所有的神经元都需要经理类似的过程，这便是反向传播过程。

2.3 梯度下降

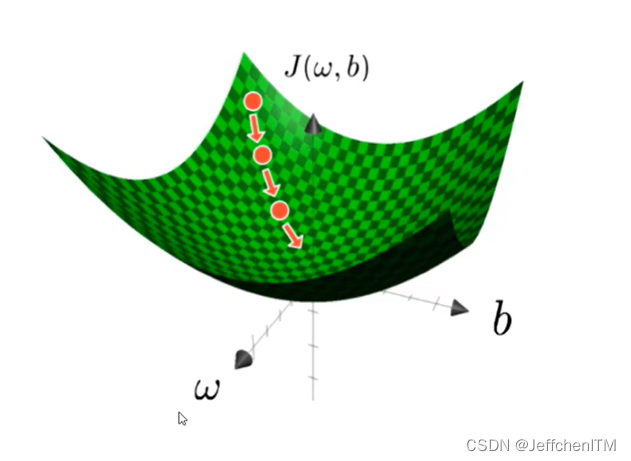
深度学习算法运行的最终目标是寻找损失函数J（w,b）的最小值

寻找最小值的方法便是梯度下降

梯度下降的核心作用是更新参数

梯度下降的核心思想是不断地尝试，一步一步试出这个最小值

梯度下降的过程如下

参数更新过程的理解

学习率的设置：

学习率是比较重要的超参数，通常学习率不能太大也不能太小

太大---容易导致不收敛

太小---则会学习的太慢

两种情况产生的后果如下图所示

3?常见的优化算法介绍

3.1??梯度下降算法（batch gradient descent BGD）

每次迭代都需要把所有样本都送入，这样的好处是每次迭代都顾及了全部的样本，做的是全局最优化,但是有可能达到局部最优。

3.2???随机梯度下降法 (Stochastic gradient descent SGD)

针对梯度下降算法训练速度过慢的缺点，提出了随机梯度下降算法，随机梯度下降算法算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。

3.3?小批量梯度下降 (Mini-batch gradient descent MBGD)

SGD相对来说要快很多，但是也有存在问题，由于单个样本的训练可能会带来很多噪声，使得SGD并不是每次迭代都向着整体最优化方向，因此在刚开始训练时可能收敛得很快，但是训练一段时间后就会变得很慢。在此基础上又提出了小批量梯度下降法，它是每次从样本中随机抽取一小批进行训练，而不是一组，这样即保证了效果又保证的速度。

3.4?动量法

mini-batch SGD算法虽然这种算法能够带来很好的训练速度，但是在到达最优点的时候并不能够总是真正到达最优点，而是在最优点附近徘徊。

另一个缺点就是mini-batch SGD需要我们挑选一个合适的学习率，当我们采用小的学习率的时候，会导致网络在训练的时候收敛太慢；当我们采用大的学习率的时候，会导致在训练过程中优化的幅度跳过函数的范围，也就是可能跳过最优点。我们所希望的仅仅是网络在优化的时候网络的损失函数有一个很好的收敛速度同时又不至于摆动幅度太大。

所以Momentum优化器刚好可以解决我们所面临的问题，它主要是基于梯度的移动指数加权平均，对网络的梯度进行平滑处理的，让梯度的摆动幅度变得更小。