[人工智能]PyTorch----激活函数

什么是激活函数？

• 在神经网络中我们经常使用线性运算来解决分类问题，这就需要激活函数来解决非线性问题

• 传统的全连接网络是让数据不断的通过线性函数和激活函数层，从而得到最终的预测结果。

Sigmoid函数

sigmoid函数是最经典、最早使用的激活函数，公式如下：

$\rho =\frac{1}{1+e^{?z}}$

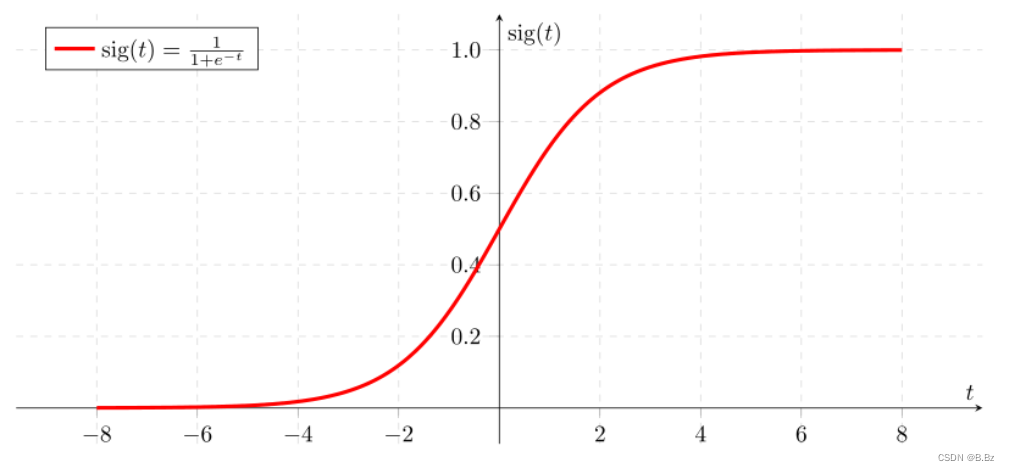
• 激活函数Sigmoid在定义域内处处可以求导，当输入一个较小或者较大的数据时，该函数的导数会变得很小，梯度趋近于0。
• 如果每次梯度值都减小，神经网络具有很多层，当梯度穿过很多层，会逐渐趋近于0，出现梯度消失现象,模型无法继续收敛，sigmoid函数以前被广泛使用，现在很少被人使用。

import torch
import torch.nn as nn
# 实现方式1
x = torch.tensor([-1.0,1.0,2.0,3.0])
output = torch.sigmoid(x)
print(output)
# 实现方式2
s = nn.Sigmoid()
output = s(x)
print(output)

Tanh激活函数

• Tanh是双曲函数中的双曲正切函数.在数学中, 双曲正切函数都是由双曲正弦函数和双曲余弦函数推导而来

• $tanh(x)=\frac{e^x?e^{?x}}{e^x+e^{?x}}$

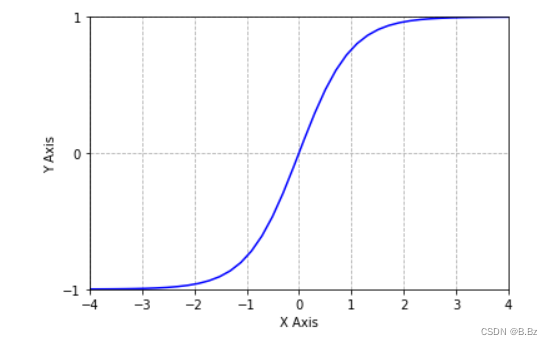
• 和Sigmoid函数很相似，但是Tanh函数的输出范围为(-1，1)，Sigmoid函数的输出范围为（0，1）。
• PyTorch中同样有两种实现方式

import torch
import torch.nn as nn
# 方式1
output = torch.tanh(x)
print(output)
# 方式2
t = nn.Tanh()
output = t(x)
print(output)

ReLU激活函数

• 双曲正切函数和Sigmoid函数都差不多，都有梯度消失的现象，解析式中也存在幂运算，计算的时间也慢。

• 为了解决梯度消失的问题，线性修正单元函数(Rectified Linear Units，简称ReLU) 就被发明了出来。

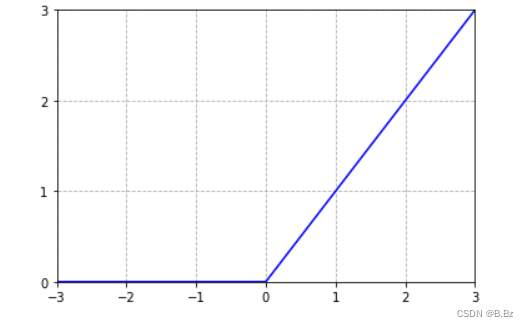
ReLU函数是现在最常用的激活函数之一：

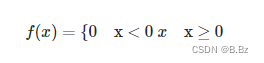
• x为常数，当x<0时，ReLU全部取值为0，梯度也为0，减少了梯度运算的成本。

• 当x>=0时，ReLU的取值为x，梯度始终为固定的一个值，解决了梯度消失的问题。
  

import torch
import torch.nn as nn
# 方式1
output = torch.relu(x)
print(output)
# 方式2
t = nn.ReLU()
output = t(x)
print(output)

总结

• 解决二分类问题, 我们一般会将最后一层设置为Sigmoid函数层. 因此, 从Sigmoid函数图像可以看出,该函数范围为(0,1) 这样可以很好的表示概率值。

• 如果在神经网络内部(隐藏层)需要使用激活函数,一般会使用ReLU函数或者ReLU函数的改进来进行激活。

• 如果是二分类问题,那么在神经网络最后一层加上Sigmoid函数层。

• 如果是多分类问题,那么会在神经网络最后一层加上Softmax函数层。

• Softmax函数通常和交叉熵函数一起使用。

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系