均方误差/MSE/二次损失/L2损失

$MSE=\frac{1}{N}\sum_{i = 1}^{N}(y-\bar{y})^2\\ 如果y和\bar{y}是向量，那么(y-\bar{y})^2=(\sqrt{\sum_{i = 1}^{m}(y_i-\bar{y_i})^2})^2$

理论上N表示batch_size，但在实现上通常还会再除以一个y向量的维度，这样并不会改变梯度方向和优化方向**

y = torch.tensor([1,2,3,0,2])
y = F.one_hot(y, 4)

out = torch.randn(5, 4)

F.mse_loss(y, out)
Out[21]: tensor(2.0983)
    
torch.mean(torch.square(y - out))
Out[21]: tensor(2.0983)
    
torch.square((y-out).norm(2)) / (4*5)
Out[21]: tensor(2.0983)

平均绝对误差/MAE/L1损失

$MAE=\frac{1}{N}\sum_{i = 1}^{N}|y-\bar{y}|\\ 如果y和\bar{y}是向量，那么|y-\bar{y}|=\sqrt{\sum_{i = 1}^{m}(y_i-\bar{y_i})^2}$

使用平方误差MSE更容易收敛，但使用绝对误差MAE对异常值更稳健

理论上N表示batch_size，但在实现上通常还会再除以一个y向量的维度，这样并不会改变梯度方向和优化方向**

y = torch.tensor([1,2,3,0,2])
y = F.one_hot(y, 4)

out = torch.randn(5, 4)

F.l1_loss(y.float(), out)
Out[25]: tensor(1.0248)
    
torch.mean(torch.abs(y-out))
Out[27]: tensor(1.0248)
    
(y-out).norm(1) / (4*5)
Out[28]: tensor(1.0248)

交叉熵损失/Cross Entropy

熵

熵越小信息量越大越不稳定惊喜度越大
$连续：Entropy=-\int plog_2p\\ 离散：Entropy=-\sum_{i}p_ilog_2p_i$

交叉熵

$H(p,q)=-\sum_{i}p_ilog_2q_i\\ H(p,q)=H(p)+KL(p||q)\\ 注：H(p,q)和H(p)可以直接计算，KL(p||q)通过H(p,q)-H(p)来计算\\ 对于独热编码，其熵为0，例如H(p:[0,1,0])=-(0*log_20+1*log_21+0*log_20)=0\\ H(p,q)若p为独热编码[0,1,0]，则H(p,q)=KL(p||q)=-log_2q_1，若p,q相同则H(p,q)=0\\ 所以其可以作为分类任务的目标函数(p为label，q为out)，H(p,q)越小p和q越接近$

$特别的，对于二分类任务：\\ H(p,q)=-(plog_2q+(1-p)log_2(1-q))\\ 其中，p为真实是正例的概率，q是预测是正例的概率。$

理论上对数以2为底，但是实践上通常对数以e为底，这样并不会改变梯度方向和优化方向**

Pytorch中 CrossEntropyLoss = LogSoftmax + NLLLoss

NLLLoss(negative log likelihood loss)
$H(p,q)=-\sum_{i}p_ilogq_i\\ 先对q做softmax:H(p,q)=-\sum_{i}p_ilog\frac{exp(q_i)}{\sum_{j}exp(q_j)}\\ 假设p为one\_hot且p_k\neq0，则\\ H(p,q)=-log\frac{exp(q_k)}{\sum_{j}exp(q_j)}=-q_k+log\sum_{j}exp(q_j)$

$CrossEntropyLoss:H(p,q)=-log\frac{exp(q_k)}{\sum_{j}exp(q_j)} =-q_k+log\sum_{j}exp(q_j)\\ LogSoftmax(x_i)=log\frac{exp(x_i)}{\sum_{j}exp(x_j)}\\ NLLLoss(p,q)=-q_k\:\:\:\:(p为one\_hot且p_k\neq0)$

out
Out[91]: 
tensor([[-1.9675, -0.0030,  1.4072,  0.6208],
        [-1.1345, -0.5482,  0.9298,  1.0552],
        [ 1.1224,  1.8556,  0.0283,  1.6605],
        [ 0.5614, -0.2457, -0.4221, -1.6666],
        [ 0.8162, -0.9078, -1.0052, -0.2580]])
y
Out[92]: tensor([1, 2, 3, 0, 2])
    
#  LogSoftmax
torch.log(F.softmax(out, dim=1))
Out[94]: 
tensor([[-3.9250, -1.9605, -0.5503, -1.3367],
        [-2.9760, -2.3897, -0.9117, -0.7864],
        [-1.6350, -0.9018, -2.7290, -1.0969],
        [-0.6564, -1.4636, -1.6399, -2.8844],
        [-0.5198, -2.2438, -2.3413, -1.5941]])

F.log_softmax(out, dim=1)
Out[95]: 
tensor([[-3.9250, -1.9605, -0.5503, -1.3367],
        [-2.9760, -2.3897, -0.9117, -0.7864],
        [-1.6350, -0.9018, -2.7290, -1.0969],
        [-0.6564, -1.4636, -1.6399, -2.8844],
        [-0.5198, -2.2438, -2.3413, -1.5941]])

# NLLLoss
-out[[0,1,2,3,4], y]
Out[106]: tensor([ 0.0030, -0.9298, -1.6605, -0.5614,  1.0052])
    
F.nll_loss(out, y, reduction='none')
Out[107]: tensor([ 0.0030, -0.9298, -1.6605, -0.5614,  1.0052])
    
# CrossEntropyLoss
# 不加reduction='none'则取均值
F.cross_entropy(out, y, reduction='none')
Out[108]: tensor([1.9605, 0.9117, 1.0969, 0.6564, 2.3413])
    
F.nll_loss(F.log_softmax(out, dim=1), y, reduction='none')
Out[109]: tensor([1.9605, 0.9117, 1.0969, 0.6564, 2.3413])
    
- out[[0,1,2,3,4], y] + torch.log(torch.sum(torch.exp(out), dim=1))
Out[111]: tensor([1.9605, 0.9117, 1.0969, 0.6564, 2.3413])

Info NCE

对比学习，有的称为自监督学习/无监督学习（实际上自监督学习是无监督学习的一种形式）。目标就是聚类。

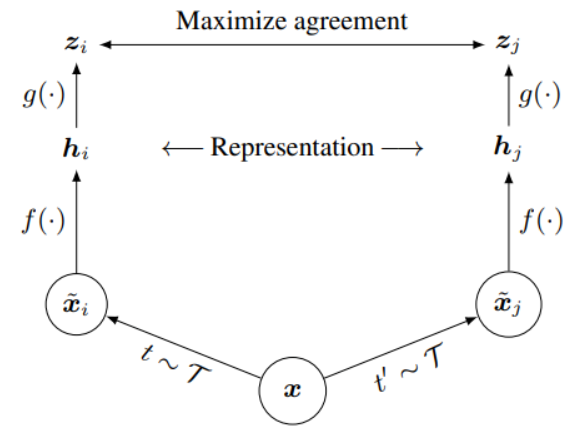
代理任务（pretext task）+目标函数（objective function）

代理任务定义正负样本（实际上就是为样本生成一个label），目标函数最大化一致。

例如上图：代理任务对于同一样本x生成xi和xj两个样本；特征提取；MLP映射；优化损失。

Information Noise Contrastive Estimation，该损失函数在数学上比CrossEntropyLoss仅多一个温度系数
$Info\_NCE=-log\frac{exp(q·k_+/\tau)}{\sum_{j}exp(q·k_j/\tau)}\\ q\:k均为特征向量,k_+和q同类，k_j(j\neq+)和q不同类$

例如现有batch_size个图片x，通过代理任务（例如旋转，裁剪等操作）生成两种图片x_q和x_k（均为batch_size个，共2*batch_size个图片）。经过特征图提取，MLP映射之后得到q shape[batch_size, feature_len]，k shape[batch_size, feature_len]。q和k对应位置的特征向量表示的是同一张图片（同类），通过Info NCE可以最大化其相关性，同时最小化与其他负例的相关性。
$处理1：q_i有k_i\:1个正例，k_j(j\neq i)\:(b-1)个负例，q·k^T得到[b, b]的矩阵，\\ 第i行的主对角线元素为q_i与对应的k_+的相关性分数\\\\ 处理2：q_i有q_i,k_i\:2个正例，q_j,k_j(j\neq i)\:(2b-2)个负例，[q,k]·[q,k]^T得到[2b, 2b]的矩阵，\\ 第i行（i\in[1,batch\_size]）的第b+i个元素为q_i与对应的k_+的相关性分数\\ 第i行（i\in[batch\_size+1,2*batch\_size]）的第b+i个元素为q_i与对应的k_+的相关性分数\\$

import torch
from torch.nn import functional as F

# 温度系数
tau = 1
batch_size = 4
feature_len = 10
q = torch.randn(batch_size, feature_len)
k = torch.randn(batch_size, feature_len)


# 处理1
# k+在每一行的位置
position_positive = torch.arange(batch_size)
# cross_entropy不加reduction='none'则包含取均值的操作即 batch_size行共batch_size个值取均值
info_nce = F.cross_entropy(q@k.t()/tau, position_positive)

# 处理2
# k+在每一行的位置
position_positive = torch.cat((torch.arange(batch_size) + batch_size, torch.arange(batch_size)))
qk = torch.cat((q, k), dim=0)
info_nce = F.cross_entropy(qk@qk.t()/tau, position_positive)