简介
k 近邻算法,kNN
- 采用测量不同特征值之间的距离方法进行分类
(1)只选择样本数据集中前k个最相似的数据,这就是 k-近邻算法中k的出处,通常k<20;
(2)选择k个最相似数据中出现次数最多的分类,作为新数据的分类;
(3)适用数据范围:数值型和标称型;
- 优缺点
(1)优点:精度高、对异常值不敏感、无数据输入假定。
(2)缺点:计算复杂度高、空间复杂度高,无法给出数据的内在含义。
- 对未知类别属性的数据集中的每个点依次执行以下操作:
(1)计算已知类别数据集中的点与当前点之间的距离;
(2)按照距离递增次序排序;
(3)选取与当前点距离最小的 k 个点;
(4)确定前 k 个点所在类别的出现频率;
(5)返回前 k 个点出现频率最高的类别作为当前点的预测分类。
sample code(基于mimist手写数字数据集)
import numpy as np
import struct
from numpy import *
import operator
import matplotlib.pyplot as plt
from os import listdir
feature_num = 3
dataSetNum = 1000
"""
训练集文件 60000个
TRAINING SET IMAGE FILE (train-images-idx3-ubyte):
[offset] [type] [value] [description]
0000 32 bit int 0x00000803(2051) magic number
0004 32 bit int 60000 number of images
0008 32 bit int 28 number of rows
0012 32 bit int 28 number of columns
0016 unsigned byte ?? pixel
0017 unsigned byte ?? pixel
"""
train_images_idx3_ubyte_file = 'MNIST_data/train-images.idx3-ubyte'
"""
训练集标签文件
TRAINING SET LABEL FILE (train-labels-idx1-ubyte):
[offset] [type] [value] [description]
0000 32 bit int 0x00000801(2049) magic number (MSB first)
0004 32 bit int 60000 number of items
0008 unsigned byte ?? label
0009 unsigned byte ?? label
"""
train_labels_idx1_ubyte_file = 'MNIST_data/train-labels.idx1-ubyte'
test_images_idx3_ubyte_file = 'MNIST_data/t10k-images.idx3-ubyte'
test_labels_idx1_ubyte_file = 'MNIST_data/t10k-labels.idx1-ubyte'
"""
解析idx3文件的通用函数
param idx3_ubyte_file: idx3文件路径
return: 数据集
"""
def decode_idx3_ubyte(idx3_ubyte_file):
bin_data = open(idx3_ubyte_file, 'rb').read()
offset = 0
fmt_header = '>iiii'
magic_number, num_images, num_rows, num_cols = struct.unpack_from(fmt_header, bin_data, offset)
if 1:
num_images = dataSetNum
print('魔数:%d, 图片数量: %d张, 图片大小: %d*%d' % (magic_number, num_images, num_rows, num_cols))
image_size = num_rows * num_cols
offset += struct.calcsize(fmt_header)
fmt_image = '>' + str(image_size) + 'B'
print(fmt_image, offset, struct.calcsize(fmt_image))
images = np.empty((num_images, num_rows* num_cols))
for i in range(num_images):
if (i + 1) % 10000 == 0:
print('已解析 %d, offset:%d' % (i + 1, offset))
images[i] = np.array(struct.unpack_from(fmt_image, bin_data, offset)).reshape((1, 784))
offset += struct.calcsize(fmt_image)
return images
"""
解析idx1文件的通用函数
:param idx1_ubyte_file: idx1文件路径
:return: 数据集
"""
def decode_idx1_ubyte(idx1_ubyte_file):
bin_data = open(idx1_ubyte_file, 'rb').read()
offset = 0
fmt_header = '>ii'
magic_number, num_images = struct.unpack_from(fmt_header, bin_data, offset)
if 1:
num_images = dataSetNum
print('魔数:%d, 图片数量: %d张' % (magic_number, num_images))
offset += struct.calcsize(fmt_header)
fmt_image = '>B'
labels = np.empty(num_images)
for i in range(num_images):
if (i + 1) % 10000 == 0:
print('已解析 %d, offset:%d' % (i + 1, offset))
labels[i] = struct.unpack_from(fmt_image, bin_data, offset)[0]
offset += struct.calcsize(fmt_image)
return labels
"""
:param idx_ubyte_file: idx文件路径
:return: n*row*col维np.array对象,n为图片数量
"""
def load_train_images(idx_ubyte_file=train_images_idx3_ubyte_file):
return decode_idx3_ubyte(idx_ubyte_file)
"""
:param idx_ubyte_file: idx文件路径
:return: n*1维np.array对象,n为图片数量
"""
def load_train_labels(idx_ubyte_file=train_labels_idx1_ubyte_file):
return decode_idx1_ubyte(idx_ubyte_file)
def load_test_images(idx_ubyte_file=test_images_idx3_ubyte_file):
return decode_idx3_ubyte(idx_ubyte_file)
def load_test_labels(idx_ubyte_file=test_labels_idx1_ubyte_file):
return decode_idx1_ubyte(idx_ubyte_file)
def classify0 (inX,dataSet,labels,k):
dataSetSize = dataSet.shape[0]
diff1 = tile(inX, (dataSetSize,1)) - dataSet
diff2 = diff1**2
diff3 = diff2.sum(axis=1)
diff4 = diff3**0.5
diff = diff4.argsort()
classCount={}
for i in range (k):
voteIlabel = labels[diff[i]]
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
sortedClassCount = sorted( classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
def handwritingClassTest():
train_images = load_train_images()
train_labels = load_train_labels()
test_images = load_test_images()
test_labels = load_test_labels()
errorCount = 0.0
mTest = len(test_labels)
for i in range(mTest):
classifierResult = classify0(test_images[i], train_images, train_labels, feature_num)
print("the classifier came back with: %d, the real answer is: %d" %(classifierResult, test_labels[i]))
if (classifierResult != test_labels[i]): errorCount += 1.0
print("\nthe total number of errors is: %d, error rate is: %f" % (errorCount, (errorCount/float(mTest))))
if __name__ == '__main__':
if 1:
handwritingClassTest()
else:
train_images = load_train_images()
train_labels = load_train_labels()
test_images = load_test_images()
test_labels = load_test_labels()
for i in range(2):
print(test_labels[i])
image_array=np.array(test_images[i]).reshape(28,28)
plt.imshow(image_array, cmap='gray')
plt.pause(0.000001)
plt.show()
print('done')
决策树
- 通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得对各个子数据集有一个最好的分类的过程。
(1)决策树的典型算法有ID3,C4.5,CART等
(2)适用数据范围:数值型和标称型;
- 优缺点
(1)优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
(2)缺点:可能会产生过度匹配问题。
- 决策树构造:
(1)特征的选择:划分数据集
?? [1] 划分数据集原则:通过信息增益将无序的数据变得更加有序
(2)决策树的生成:由训练样本集生成决策树的过程。
(3)决策树的剪枝:决策树的剪枝是对上一阶段生成的决策树进行检验、校正和修下的过程
?? [1] 主要是用测试数据集中的数据校验决策树生成过程中产生的初步规则,将那些影响预衡准确性的分枝剪除。
- 重要概念
(1)熵(Ent):表示随机变量不确定性的度量
?? [1]当数据量一致时,系统越有序/集中,熵值越低;系统越混乱或者分散,熵值越高。
?? [2] 熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大
?? [3] 当熵的概率由数据估计得到时,所对应的熵称为经验熵,
(2)信息增益:以某特征划分数据集前后的熵的差值,信息增益 = entroy(前) - entroy(后)
?? [1] 信息增益越大,熵被消除,不确定性越小,有更强的分类能力,应作为最优特征
sample code
from math import log
def creatDataSet():
dataSet=[
[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels=['年龄','有工作','有自己的房子','信贷情况']
return dataSet,labels
def calcShannonEnt(dataSet):
numEntries=len(dataSet)
print("numEntries: ", numEntries)
labelCounts={}
for featVec in dataSet:
currentLabel=featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1
print("labelCounts:", labelCounts)
shannonEnt=0.0
for key in labelCounts:
prob=float(labelCounts[key])/numEntries
shannonEnt-=prob*log(prob,2)
print("key:", key, ",\t shannonEnt 经验熵:", shannonEnt)
return shannonEnt
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
print("numFeatures:", numFeatures)
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
print("featList:", featList)
uniqueVals = set(featList)
print("uniqueVals:", uniqueVals)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
print("subDataSet:", subDataSet)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt((subDataSet))
print("newEntropy:", newEntropy )
infoGain = baseEntropy - newEntropy
print("第%d个特征的增益为%.3f" % (i, infoGain))
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
def splitDataSet(dataSet, axis, value):
retDataSet=[]
print("[splitDataSet] axis:", axis, " ,value:", value)
for featVec in dataSet:
if featVec[axis]==value:
reducedFeatVec=featVec[:axis]
print("[splitDataSet] reducedFeatVec:", reducedFeatVec)
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
print("[splitDataSet] retDataSet:", retDataSet)
return retDataSet
if __name__=='__main__':
dataSet,features = creatDataSet()
print("最优索引值:"+str(chooseBestFeatureToSplit(dataSet)))
朴素贝叶斯
- 基于贝叶斯定理与特征条件独立假设的分类方法,多用于文本分类,如垃圾邮件等
(1)结合先验概率和后验概率,即避免了只使用先验概率的主观偏见,也避免了单独使用样本信息的过拟合现象
(2)对于给定的训练集,首先基于特征条件独立假设 学习输入输出的联合概率分布;然后基于此模型,对给定的输入 x,利用贝叶斯定理求出后验概率最大的输出 y。
(3)通过学习得到模型的机制,所以属于生成模型
(4)适用数据范围:标称型;
- 优缺点
(1)优点
?? [1] 适用于大的数据集,数据较少的情况下仍然有效
?? [2] 可以处理多类别问题。
?? [3] 有稳定的分类效率
?? [4] 适合增量式训练
(2)缺点
?? [1] 对于输入数据的准备方式较为敏感
?? [4] 如果分类变量具有在训练数据集中未观察到的类别,则模型将指定0概率并且将无法进行预测。
- 朴素贝叶斯流程:
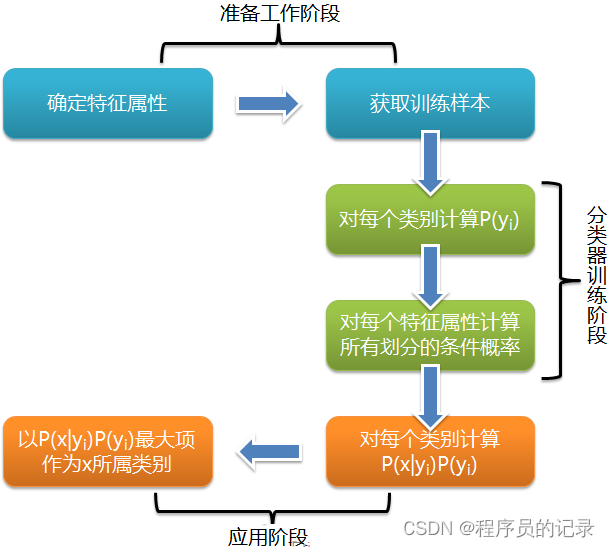
(1)零概率问题
?? [1] 原因:对文档进行分类时,要计算多个概率的乘积以获得文档属于某个类别的概率,如果其中有一个为0,则最后的结果也为0。
?? [2] 解决方法:拉普拉斯平滑,将所有词的出现次数初始化为1,并将分母初始化为2
(2)下溢出
?? [1] 原因:太多很小的数相乘,越乘越小,造成下溢出。在相应小数位置进行四舍五入,计算结果可能就变成0了。
?? [2] 解决方法:对乘积结果取自然对数
- 重要概念
(1)先验概率 P(Y):事件发生前的预判概率。可以是基于历史数据的统计,可以由背景常识得出,也可以是人的主观观点给出
(2)后验概率 P(Y∣X): 事件发生后求的反向条件概率
?? [1] 后验概率的计算要以先验概率为基础
(3)条件概率 / 似然概率 P(X∣Y) :一个事件发生后另一个事件发生的概率
- 算法对比
逻辑回归:通过拟合曲线实现分类
决策树:通过寻找最佳划分特征进而学习样本路径实现分类
支持向量机:通过寻找分类超平面进而最大化类别间隔实现分类
朴素贝叶斯:通过特征概率来预测分类
sample code
import numpy as np
def loadDataSet():
dataSet=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0,1,0,1,0,1]
return dataSet,classVec
def createVocabList(dataSet):
vocabSet = set()
for doc in dataSet:
vocabSet = vocabSet | set(doc)
vocabList = list(vocabSet)
return vocabList
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0] * len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else:
print(f" {word} is not in my Vocabulary!" )
return returnVec
def get_trainMat(dataSet):
trainMat = []
vocabList = createVocabList(dataSet)
for inputSet in dataSet:
returnVec=setOfWords2Vec(vocabList, inputSet)
trainMat.append(returnVec)
print("get_trainMat, trainMat:", trainMat)
return trainMat
def trainNB(trainMat,classVec):
n = len(trainMat)
m = len(trainMat[0])
pAb = sum(classVec)/n
p0Num = np.ones(m)
p1Num = np.ones(m)
p0Denom = 2
p1Denom = 2
for i in range(n):
if classVec[i] == 1:
p1Num += trainMat[i]
p1Denom += sum(trainMat[i])
else:
p0Num += trainMat[i]
p0Denom += sum(trainMat[i])
p1V = np.log(p1Num/p1Denom)
p0V = np.log(p0Num/p0Denom)
return p0V,p1V,pAb
def classifyNB(vec2Classify, p0V, p1V, pAb):
p1 = sum(vec2Classify * p1V) + np.log(pAb)
p0 = sum(vec2Classify * p0V) + np.log(1- pAb)
print("sum(vec2Classify * p1V):", sum(vec2Classify * p1V), "np.log(pAb):", np.log(pAb))
if p1 > p0:
return 1
else:
return 0
def testingNB(testVec):
dataSet,classVec = loadDataSet()
vocabList = createVocabList(dataSet)
trainMat= get_trainMat(dataSet)
p0V,p1V,pAb = trainNB(trainMat,classVec)
thisone = setOfWords2Vec(vocabList, testVec)
if classifyNB(thisone, p0V, p1V, pAb)==1:
print(testVec,'属于侮辱类')
else:
print(testVec,'属于非侮辱类')
testVec1 = ['love', 'my', 'dalmation']
testingNB(testVec1)
testVec2 = ['stupid', 'garbage']
testingNB(testVec2)
Logistic 回归
- 分类模型,假设数据服从 Logistic 分布,使用极大似然估计做参数的估计,常用于二分类
(1)损失函数:可通过极大似然估计或交叉熵损失函数构建
(2)适用数据范围:数值型和标称型;
(3)sigmoid函数:
h
θ
(
x
)
=
g
(
θ
T
x
)
h_\theta(x)=g(\theta^Tx)
hθ?(x)=g(θTx) = y =
1
1
+
e
?
θ
T
x
\frac{1}{1 + e^{-\theta^{T}x}}
1+e?θTx1?
?? [1] 自变量任意实数;值域 [0, 1], 预测值转为概率;
?? [2]
θ
0
\theta_0
θ0? +
θ
1
\theta_1
θ1?x_1 + … +
θ
n
\theta_n
θn?x_n=
θ
T
x
\theta^Tx
θTx
- 优缺点
(1)优点:
?? [1] 训练速度较快,分类时 计算量只和特征的数目相关;
?? [2] 简单易理解,模型的可解释性好
?? [3] 适合二分类问题,不需要缩放输入特征;
?? [4] 内存资源占用小,因为只需要存储各个维度的特征值;
(2)缺点:
?? [1] 特征空间很大时,性能不好。
?? [2] 数据特征有缺失或特征空间很大时效果不会很好
- 逻辑回归构造:
(1)先拟合决策边界
(2)建立边界与分类的概率联系,从而得到二分类情况下的概率。
- 重要概念
(1)逻辑回归模型
P
(
Y
=
1
∣
x
)
P(Y=1|x)
P(Y=1∣x) =
1
1
+
e
?
(
w
T
x
+
b
)
\frac{1}{1 + e^{-(w^Tx+b)}}
1+e?(wTx+b)1?, Y是 x 为正例的概率
?? [1]
l
n
(
o
d
d
s
)
ln(odds)
ln(odds) =
l
n
y
1
?
y
ln \frac{y}{1 - y}
ln1?yy? =
w
T
x
+
b
w^Tx + b
wTx+b =
l
n
P
(
Y
=
1
∣
x
)
1
?
P
(
Y
=
1
∣
x
)
ln \frac{P(Y=1|x)}{1 - P(Y=1|x)}
ln1?P(Y=1∣x)P(Y=1∣x)?
?? ?? a. 将 Y 视为后验概率估计
?? [2] Odds (几率, 可能性): 指某事件发生的概率与不发生的概率之比,即 odds =
p
1
1
?
p
1
\frac{p_1}{1 - p_1}
1?p1?p1??.
?? [3] 当
w
T
x
+
b
w^Tx+b
wTx+b 的值越接近正无穷,
P
(
Y
=
1
∣
x
)
P(Y=1|x)
P(Y=1∣x) 概率值越接近 1
?? [4]
(2)梯度上升法:找到函数最大值的最好方法,是沿着该函数的梯度方向探寻
?? [1] 梯度:沿x的方向移动
?
f
(
x
,
y
)
?
x
\frac{?f(x,y)}{?x}
?x?f(x,y)?,沿y的方向移动
?
f
(
x
,
y
)
?
y
\frac{?f(x,y)}{?y}
?y?f(x,y)?,函数f(x,y)必须要在待计算的点上有定义并且可微
?? [2] 梯度算子总是指向函数值增长最快的方向
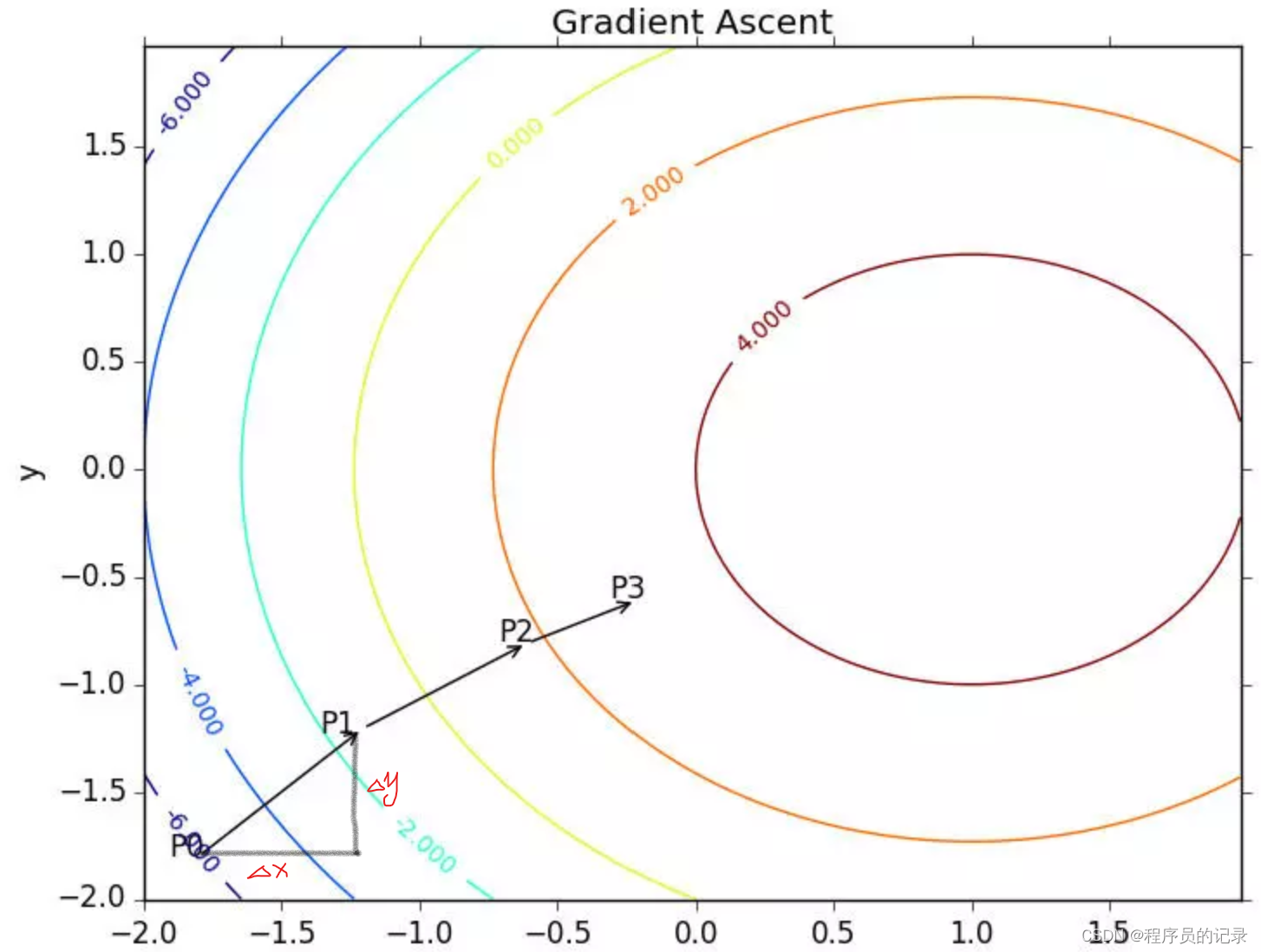
(3)P (x |
θ
\theta
θ) :x, 某一个具体的数据;
θ
\theta
θ, 模型的参数
?? [1] 概率函数:
θ
\theta
θ 是已知确定,x 是变量,描述对于不同的样本点 x 出现的概率
?? [2] 似然函数:x 是已知确定,
θ
\theta
θ 是变量,描述对于不同的模型参数,出现 x 样本点的概率
(4)决策边界(决策面): 是用于在N维空间,将不同类别样本分开的平面或曲面。
?? [1] 在逻辑回归中,决策边界由
θ
T
x
\theta^{T}x
θTx = 0 定义
?? [2] 决策边界是假设函数的属性,由参数决定,而不是由数据集的特征决定。
sample code
内容参考《机器学习实战》
|


