本次学习笔记主要记录学习深度学习时的各种记录,包括吴恩达老师视频学习、花书。作者能力有限,如有错误等,望联系修改,非常感谢!
改善深层神经网络:超参数调试、正则化以及优化(二)- 优化算法
- 一、Mini-batch 梯度下降(Mini-batch gradient descent)
- 二、理解mini-batch梯度下降法(understanding mini-batch gradient descent)
- 三、指数加权平均数(Exponentially weighted averages)
- 四、理解指数加权平均数(Understanding exponentially weighted averages)
- 五、指数加权平均的偏差修正(Bias correction in exponentially weighted averages)
- 六、动量梯度下降法(Gradient descent with Momentum)
- 七、RMSprop
- 八、Adam 优化算法(Adam optimization algorithm)
- 九、学习率衰减(Learning rate decay)
- 十、局部最优的问题(The problem of local optima)
第一版???????2022-05-23????????初稿
一、Mini-batch 梯度下降(Mini-batch gradient descent)

优化算法能够让神经网络运行得更快。
X的维数是(nx,m),Y的维数是(1,m),向量化能够相对较快的处理所有m个样本,m足够大处理速度仍慢,此时先让梯度下降法处理一部分,算法速度会更快。
可以把训练集分割为小一点的子集训练,这些子集被取名为mini-batch。x(1)到x(1000)取出来,称为X{1},以此类推。
(i)表示训练集里的值,(l)表示神经网络的层数,{t}表示不同的mini-batch。

首先对输入X{t}执行前向传播,接着计算Z[1]、A[1]到A[l]。
接着计算损失成本函数J,如图使用正则化。
然后反向传播计算J{t}的梯度,接着更新加权值。
上述为“一代(1 epoch)”的训练,一代意味着只是一次遍历了训练集。想要多次遍历训练集,还需为另一个while循环设另一个for循环,可以一直遍历训练集,直到最后能收敛到一个合适精度。
二、理解mini-batch梯度下降法(understanding mini-batch gradient descent)
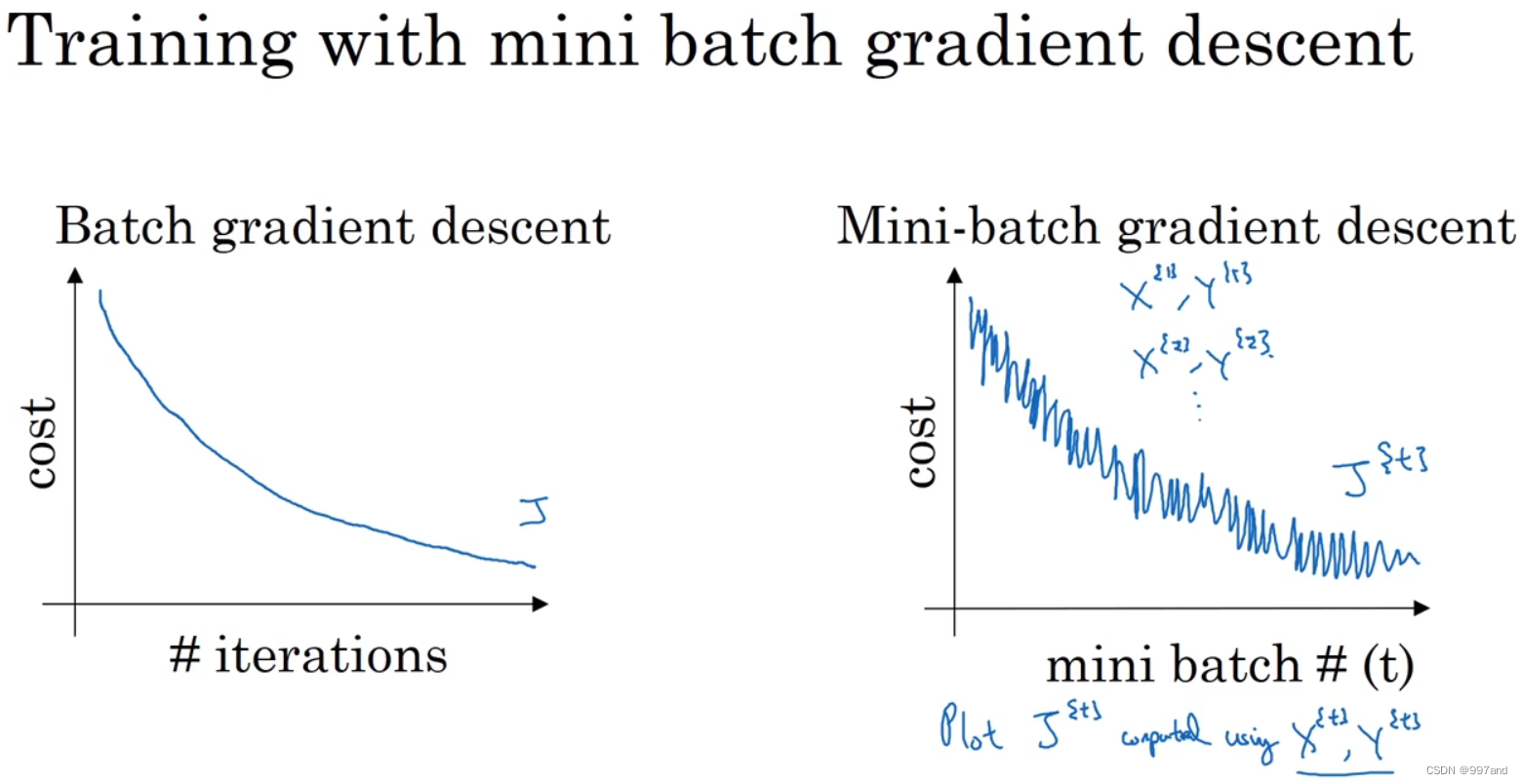
batch梯度下降法,每次迭代遍历整个训练集,可以预期每次迭代成本都会下降,如图左,若J在某次迭代增加了,那必是出问题的。
mini-batch梯度下降法,不是每次迭代都是下降的,但走势向下,如图右。噪声产生的原因在于也许X{1}和Y{1}是比较容易计算的mini-batch,因此成本会低一些。每个mini-batch的计算难度不确定,因此出现这些摆动。

极端情况下,mini-batch大小等于整个训练集大小,得到batch梯度下降法。
另一极端情况,设为1,叫随机梯度下降法,一次只处理一个。
如图紫为随机梯度下降,蓝为batch梯度下降。绿色mini-batch大小设在两者之间。
1.batch梯度下降,缺点在于训练数据集过大,单次迭代耗时长。
2.随机梯度下降,处理一个样本好,但缺点在于失去向量化带来的加速。
3.mini-batch,一方面得到大量向量化,另一方面,不需等待整个训练集被处理完就可开始后续工作。常把mini-batch的大小设为2的n次方,一般为64-512,1024较为少见。
mini-batch中,X{t}和Y{t}要符合CPU/GPU内存。
三、指数加权平均数(Exponentially weighted averages)
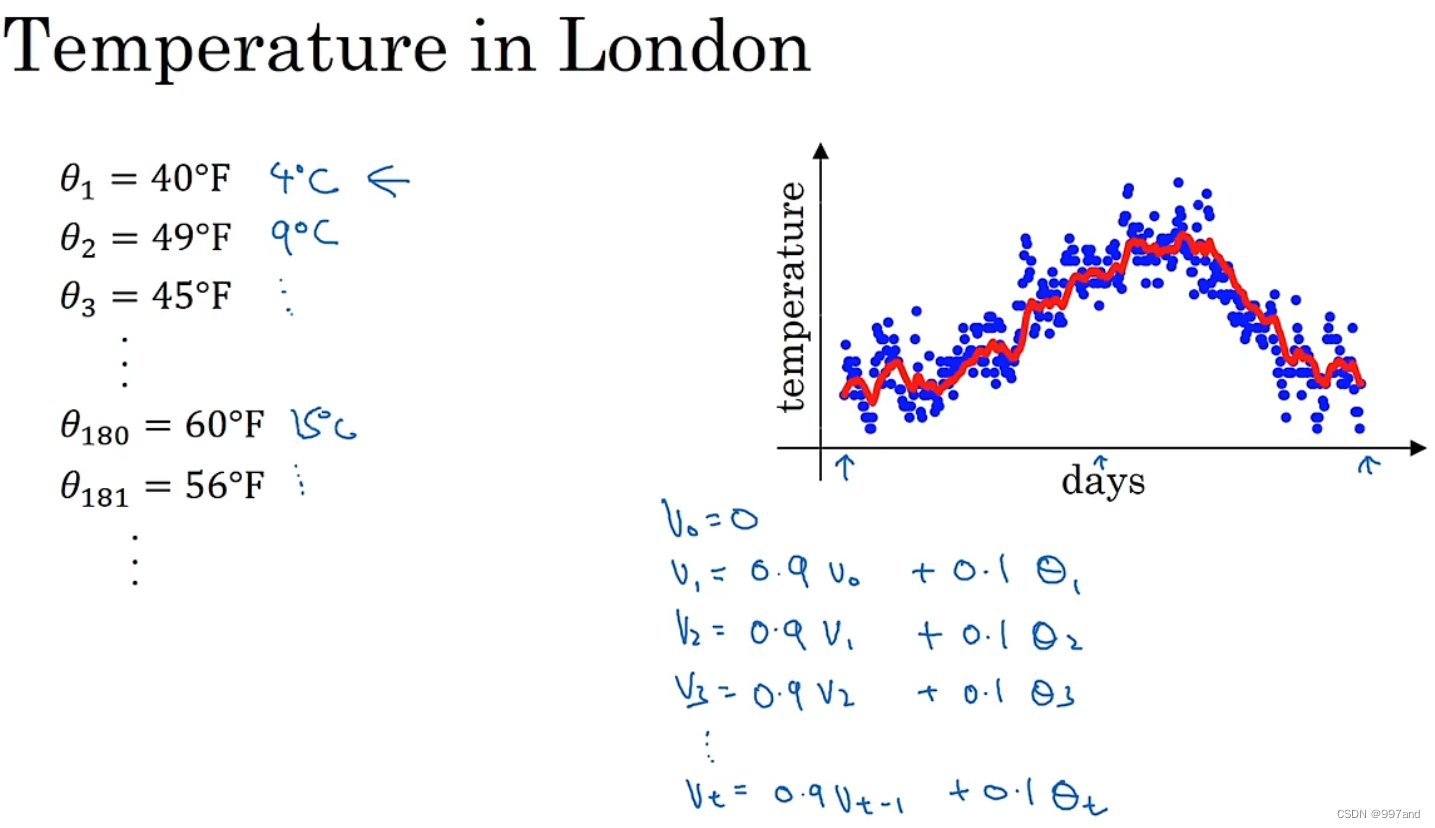
数据作图,起始日在1月份,年中接近夏季,随后就是年末。
令v0=1,然后每天使用0.9加权数之前的数值 加上 当日温度的0.1倍。
公式为:0.9v_t-1 + 0.1θ_t
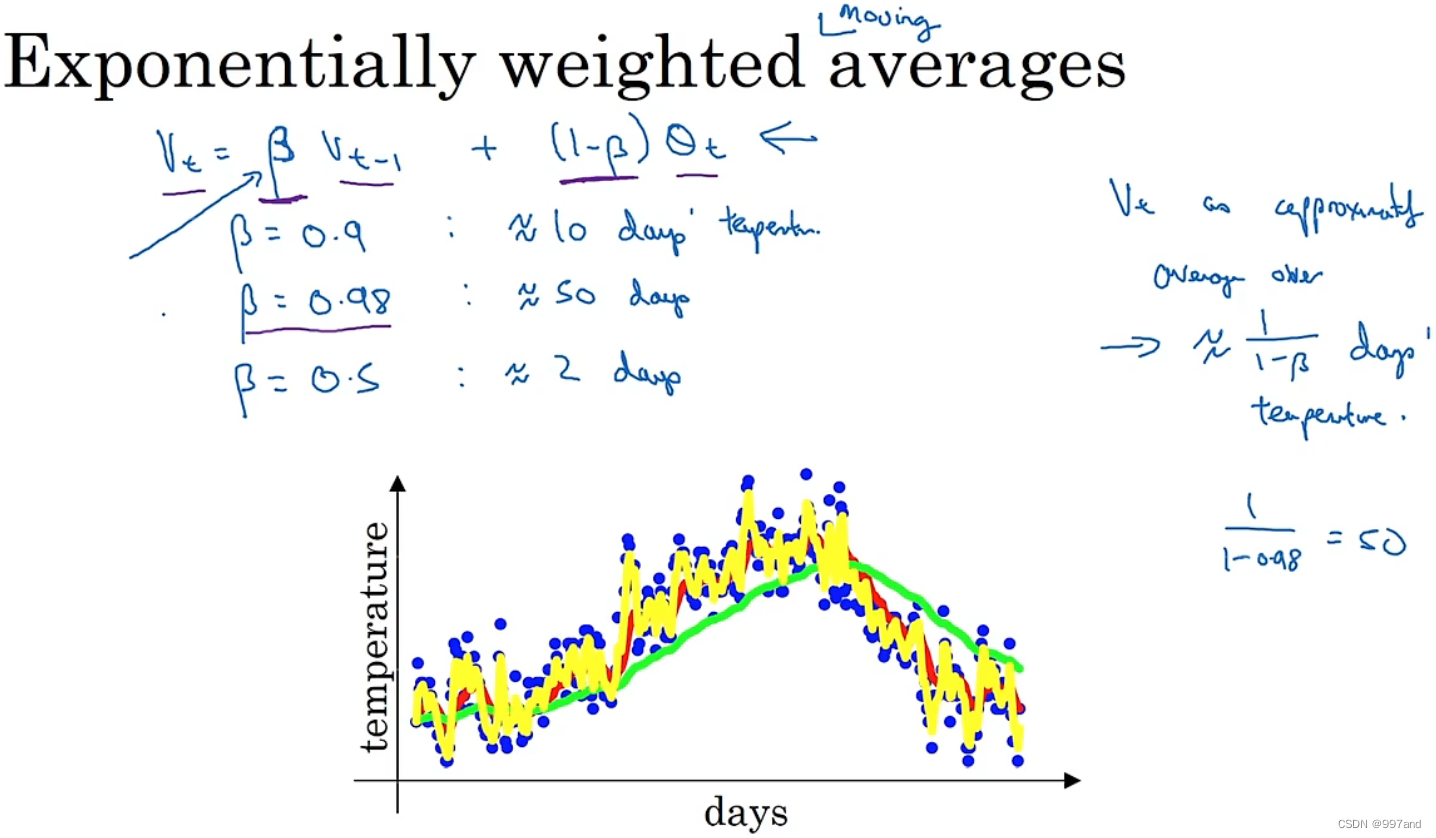
β=0.9,是十天的平均值,即红线部分。
β=0.98,过去50天的温度,即绿线部分。多平均了几天,曲线波动更小。缺点在于适应更慢些。
β=0.5,平均两天的温度,即黄线部分,所得曲线噪声更多。
四、理解指数加权平均数(Understanding exponentially weighted averages)
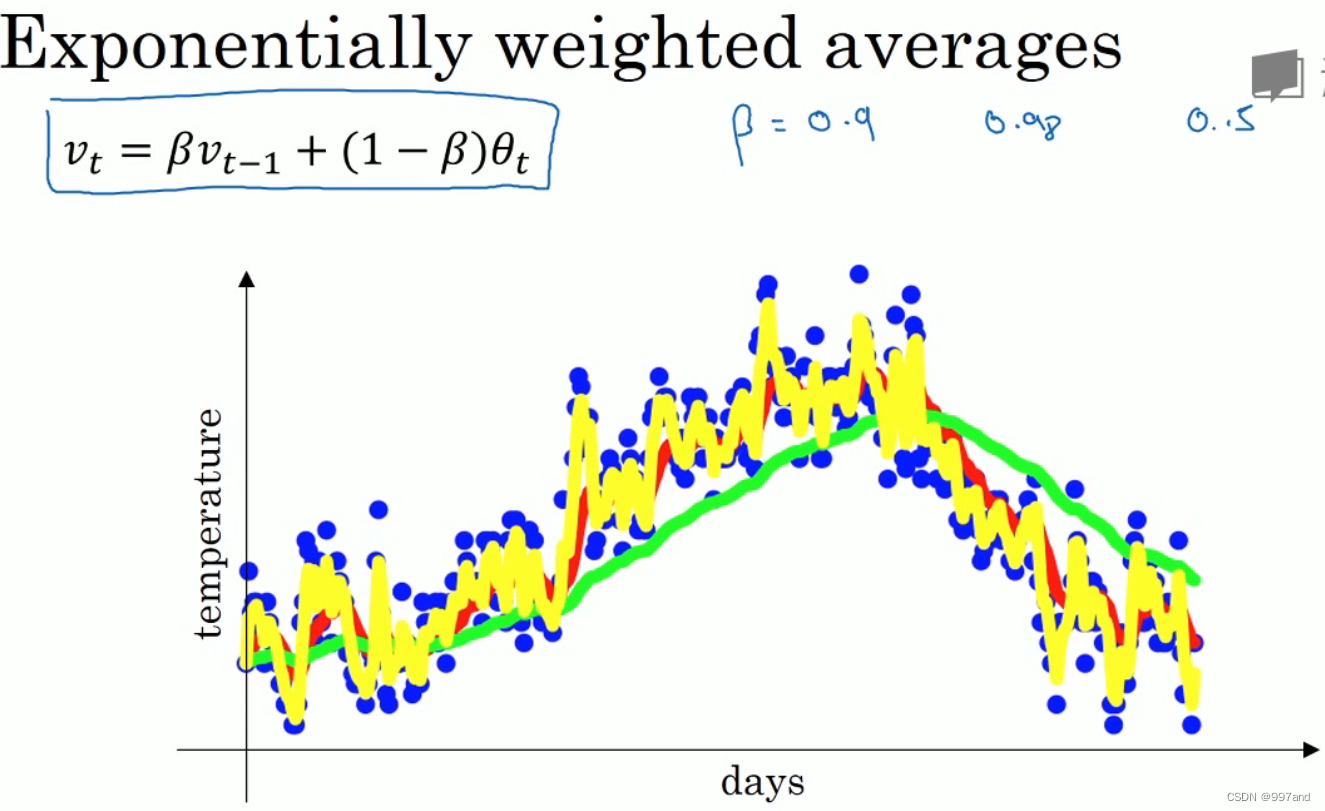
回顾2.3节。红0.9,绿0.98,黄0.5.

对v100套入,并展开,是一个加和并平均。这样有了指数衰减函数,0.1,0.1*0.9…
所有系数相加起来为1或逼近1,称为偏差修正。0.910约为0.35,大约是e/1,令ε=0.1,则(1-ε)1/ε约为1/e,大约是0.34。这是大致思想。
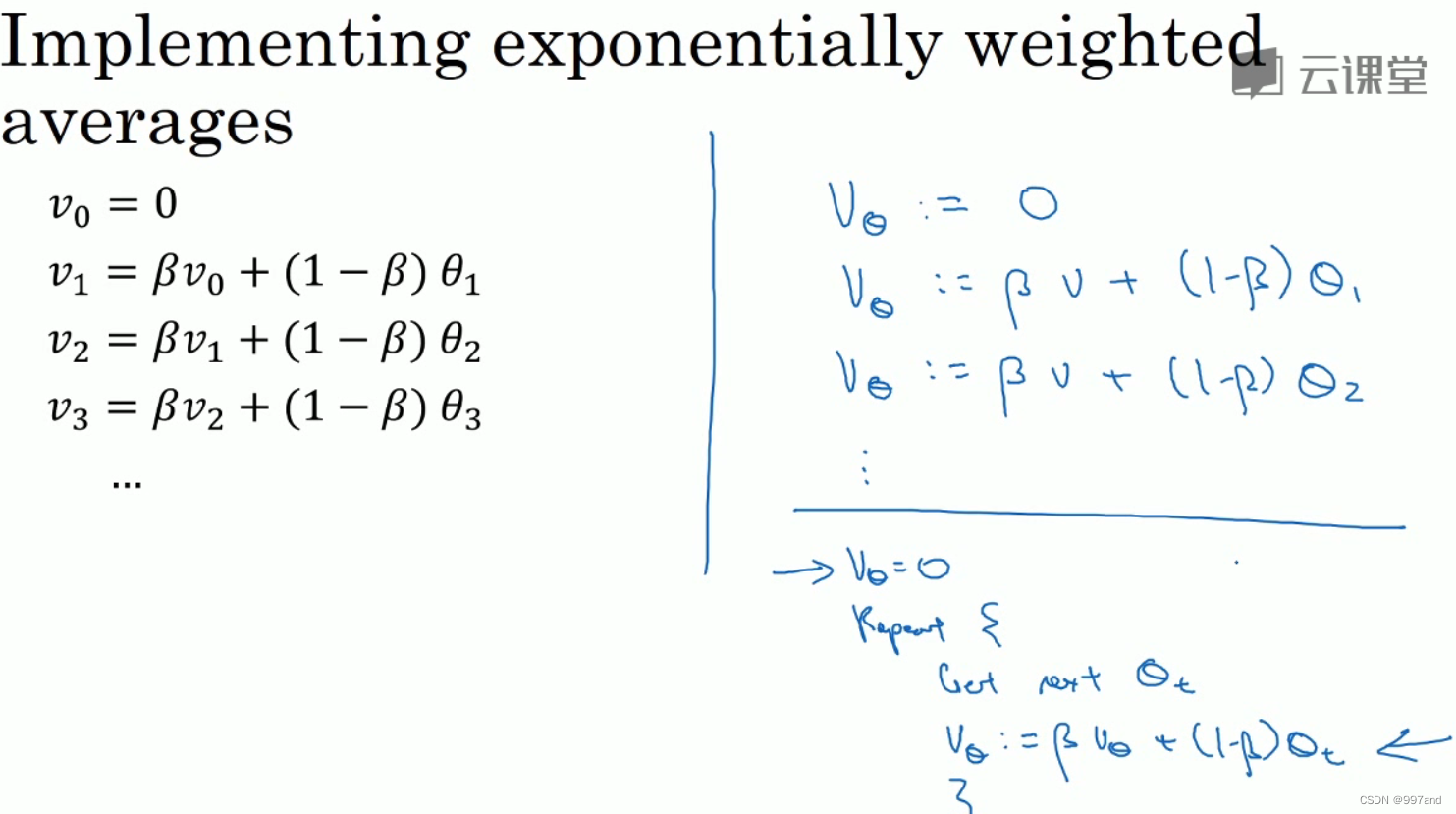
指数加权平均数公式好处之一在于,它占用极少内存。
五、指数加权平均的偏差修正(Bias correction in exponentially weighted averages)
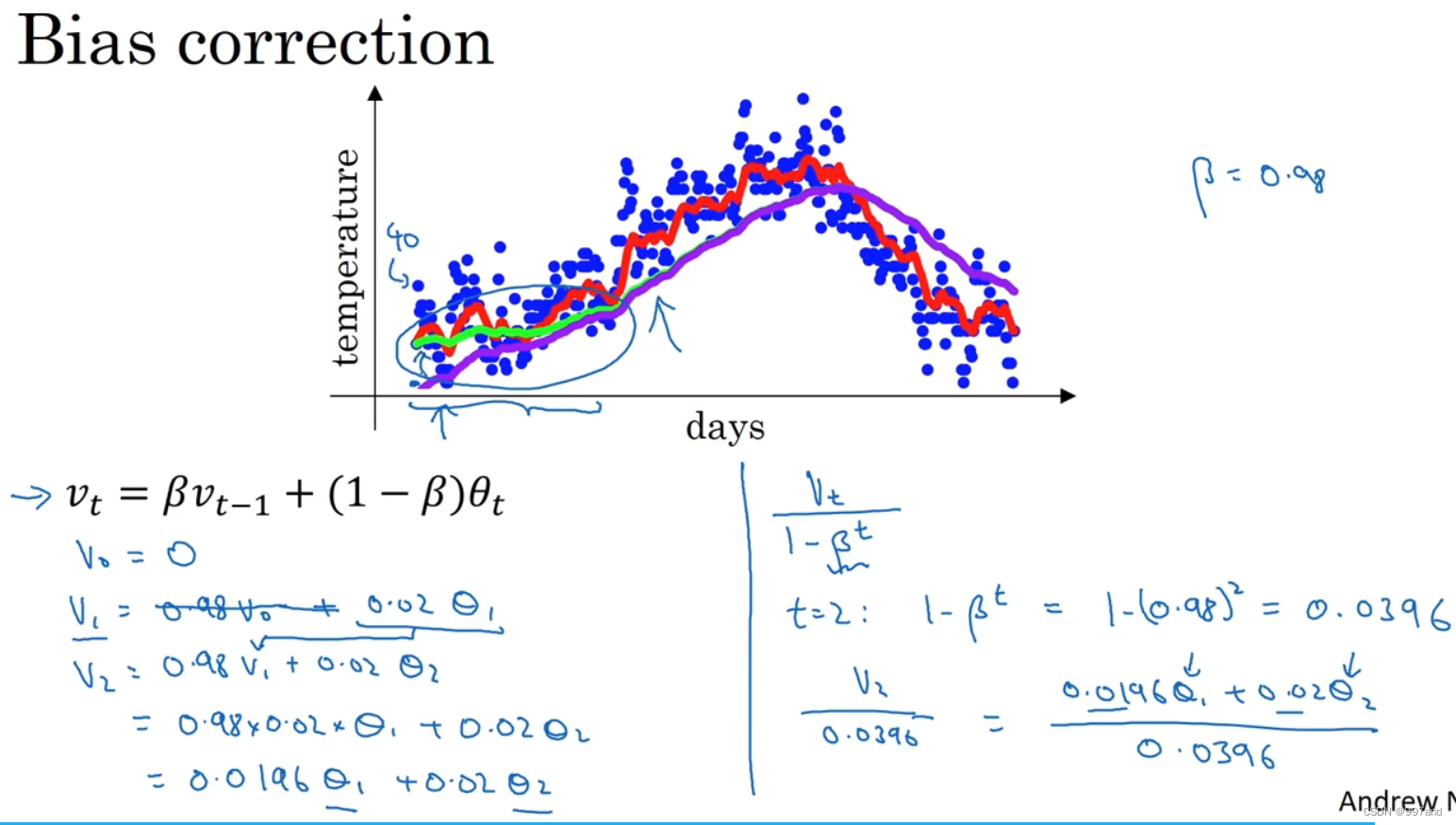
使用0.98估测不好,有个办法,即不用v_t,而用v_t/(1-β_t),t就是现在的天数。即θ1和θ2的加权平均数,并除去了偏差。t增加,βt接近于0,偏差修正几乎没用。t较大时,紫线基本和绿线重合。
六、动量梯度下降法(Gradient descent with Momentum)
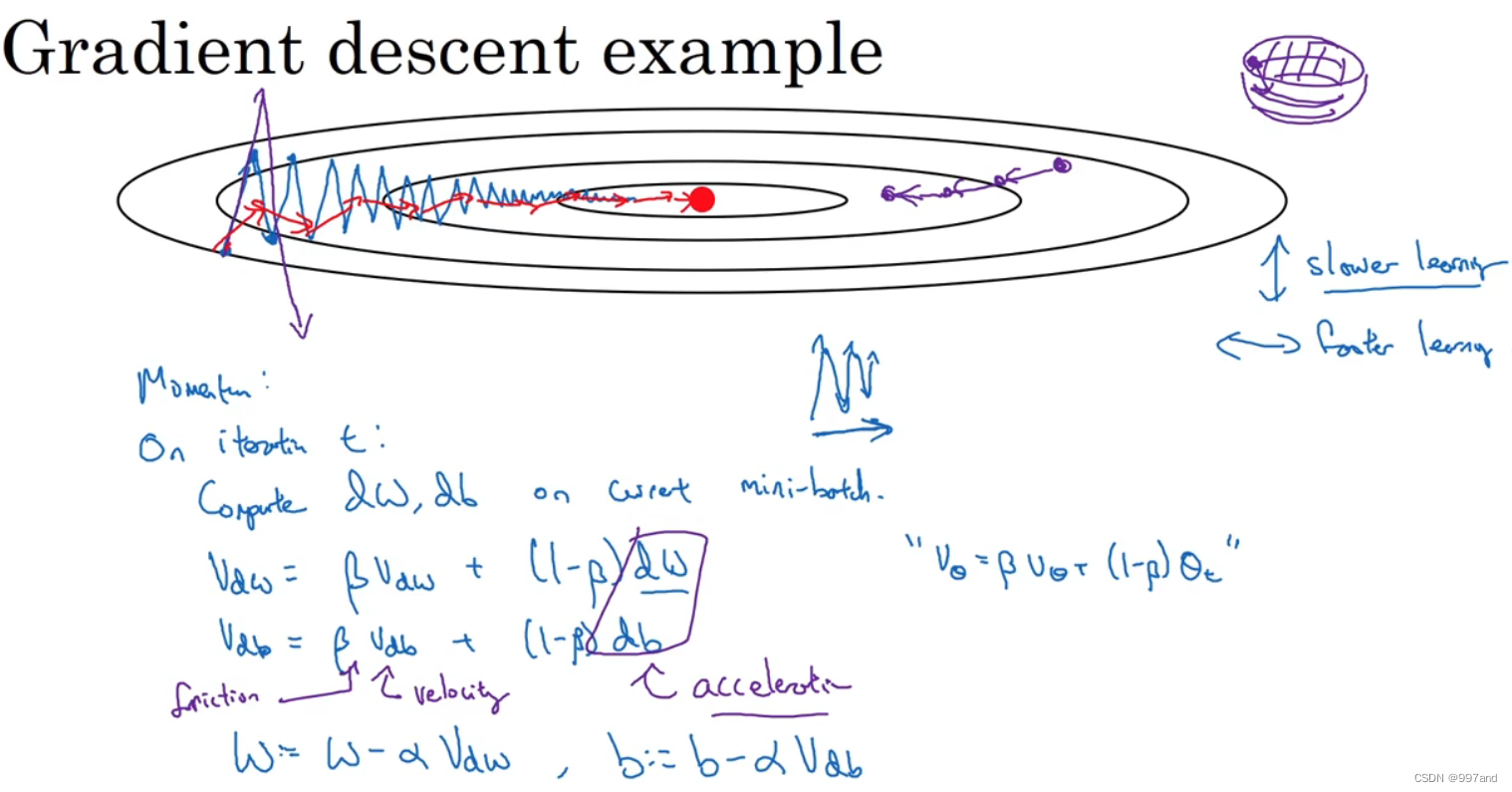
Momentum,运行速度几乎总是快于标准的梯度下降算法,基本想法是:计算梯度的指数加权平均数,并利用该梯度更新你的权重。
若要优化成本函数,如图,红点代表最小值的位置,从蓝色开始梯度下降法,较大学习率则会成紫线。
在纵轴希望慢些,不要摆动;在横轴,希望加快学习,就用到了动量梯度下降法。
需要做的是,每次迭代中,会计算微分dW,db,可用mini-batch计算。
v_dW = βv_dW + (1-β)dW
v_db = βv_db + (1-β)db,然后重新赋值
W:=W-αv_dw
b:=b-αv_db
动量梯度下降法能最小化碗装函数,

有两个超参数,α和β,β控制着指数加权平均数。v_dw初始0,v_db初始也是零向量
七、RMSprop
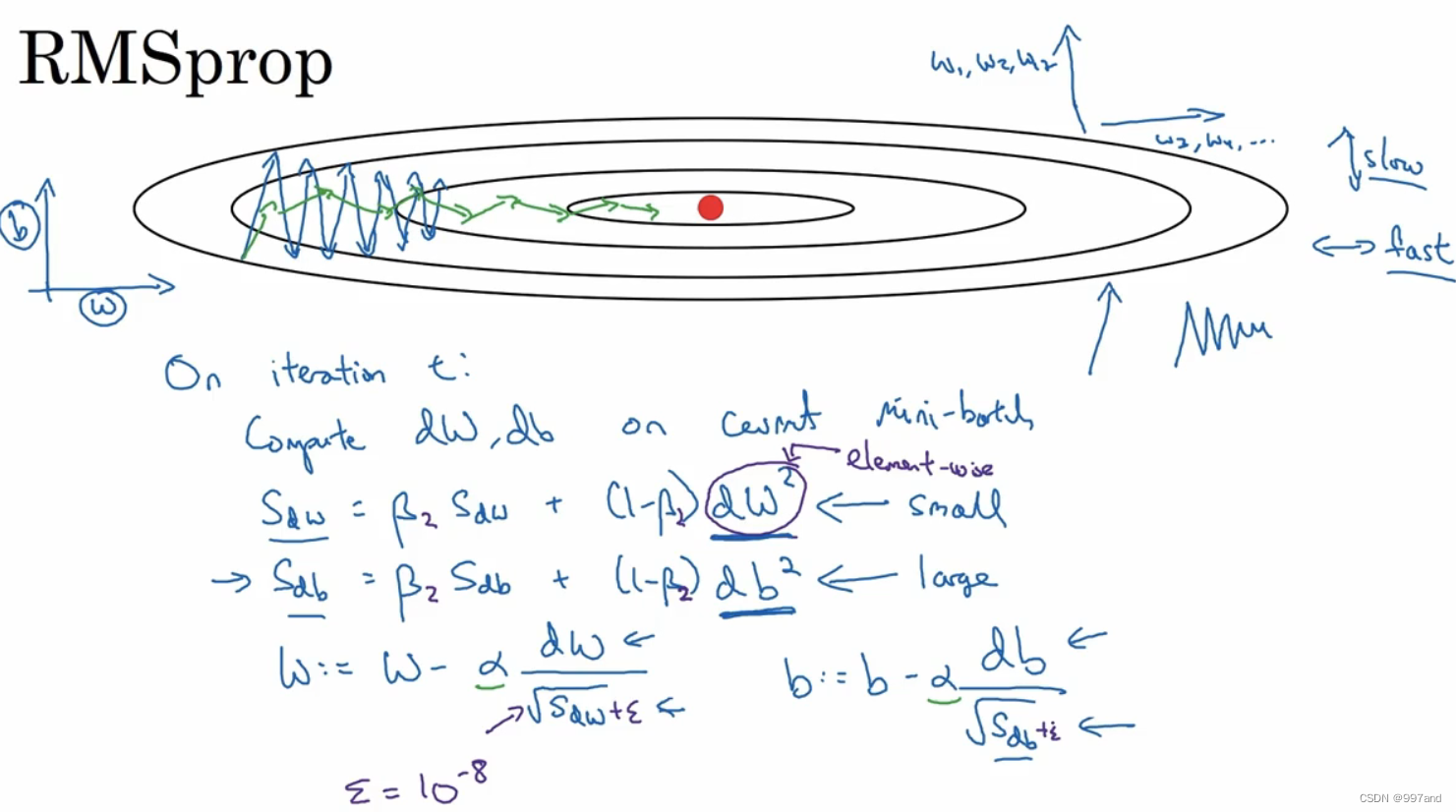
RMSprop,全称root mean square prop算法,可以加速梯度下降。
在第t次迭代中,该算法会照常计算当下mini-batch的微分dW、db,,用到新符号S_dw。如图W2数是针对这一整个符号的,这样做能保留微分平方的加权平均数。接着RMSprop会这样计算:W:=W-α(dW/根号下S_dW)、b:=b-α(db/根号下S_db)。
八、Adam 优化算法(Adam optimization algorithm)

Adam优化算法基本上是将Momentum和RMSprop结合起来。
首先,初始化;在第t次迭代中,计算微分用当前的mini-batch计算dW和db;接着计算Momentum指数加权平均数(这里β1,后边用β2);RMSprop计算;一般使用Adam算法时,要计算偏差修正;最后更新权重和b值。

本算法有很多超参数:
1.学习率α很重要,需要经常调试;
2.β1常用缺省值为0.9,这是dW的移动平均数,也是dW的加权平均数;
3.β2推荐使用0.999,是(dW)2和(db)2的移动加权平均值;
4.ε建议为10-8,并不需要设置它,因为不影响算法表现。
九、学习率衰减(Learning rate decay)
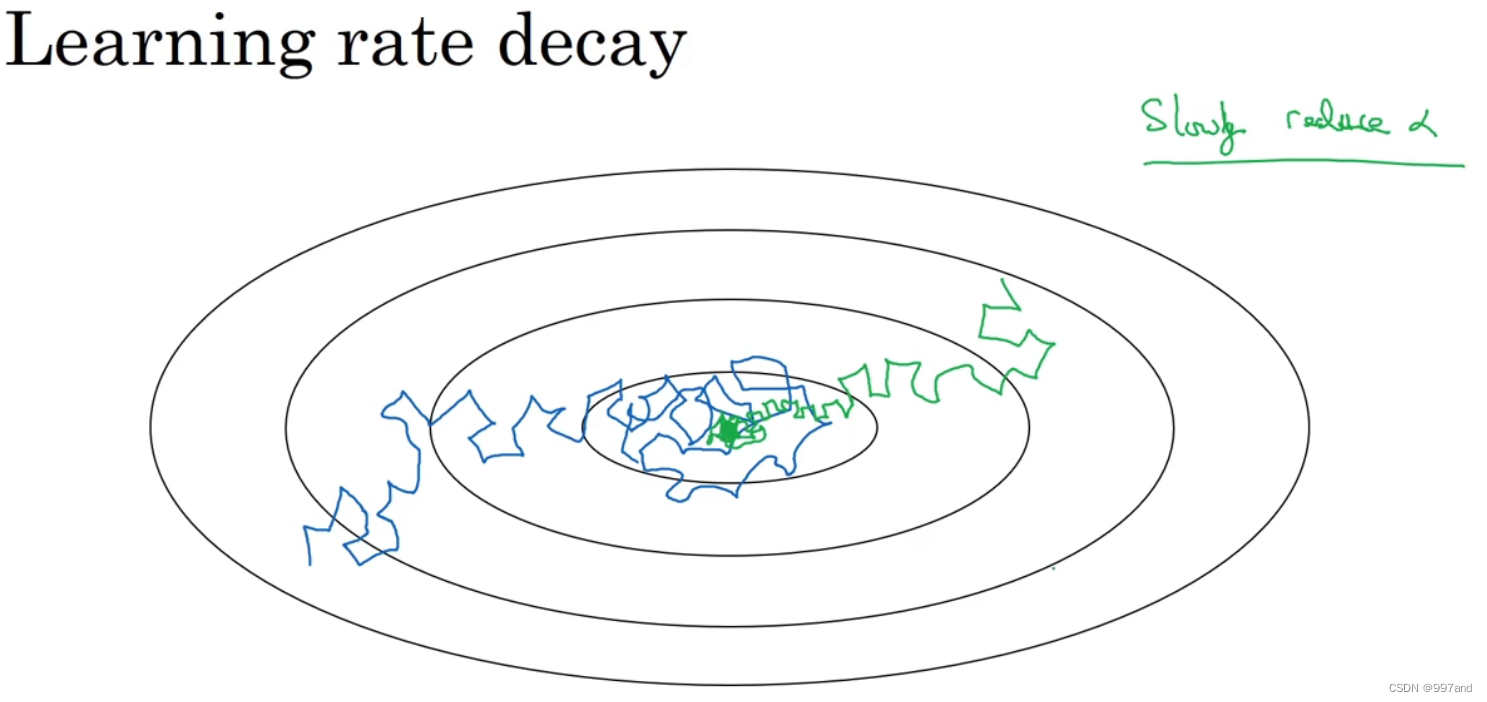
假设你要使用 mini-batch 梯度下降法,mini-batch 数量不大,大概64 或者 128个样本,
在迭代过程中会有噪音(蓝色线),下降朝向这里的最小值,但是不会精确地收敛,所以你的算法最后在附近摆动,并不会真正收敛,因为你用的a是固定值,不同的mini-batch 中有噪音。
要慢慢减少学习率α的话,在初期的时候,α学习率还较大,你的学习还是相对较快,
但随着α变小,你的步伐也会变慢变小,所以最后你的曲线(绿色线)会在最小值附近的一小块区域里摆动,而不是在训练过程中,大幅度在最小值附近摆动。
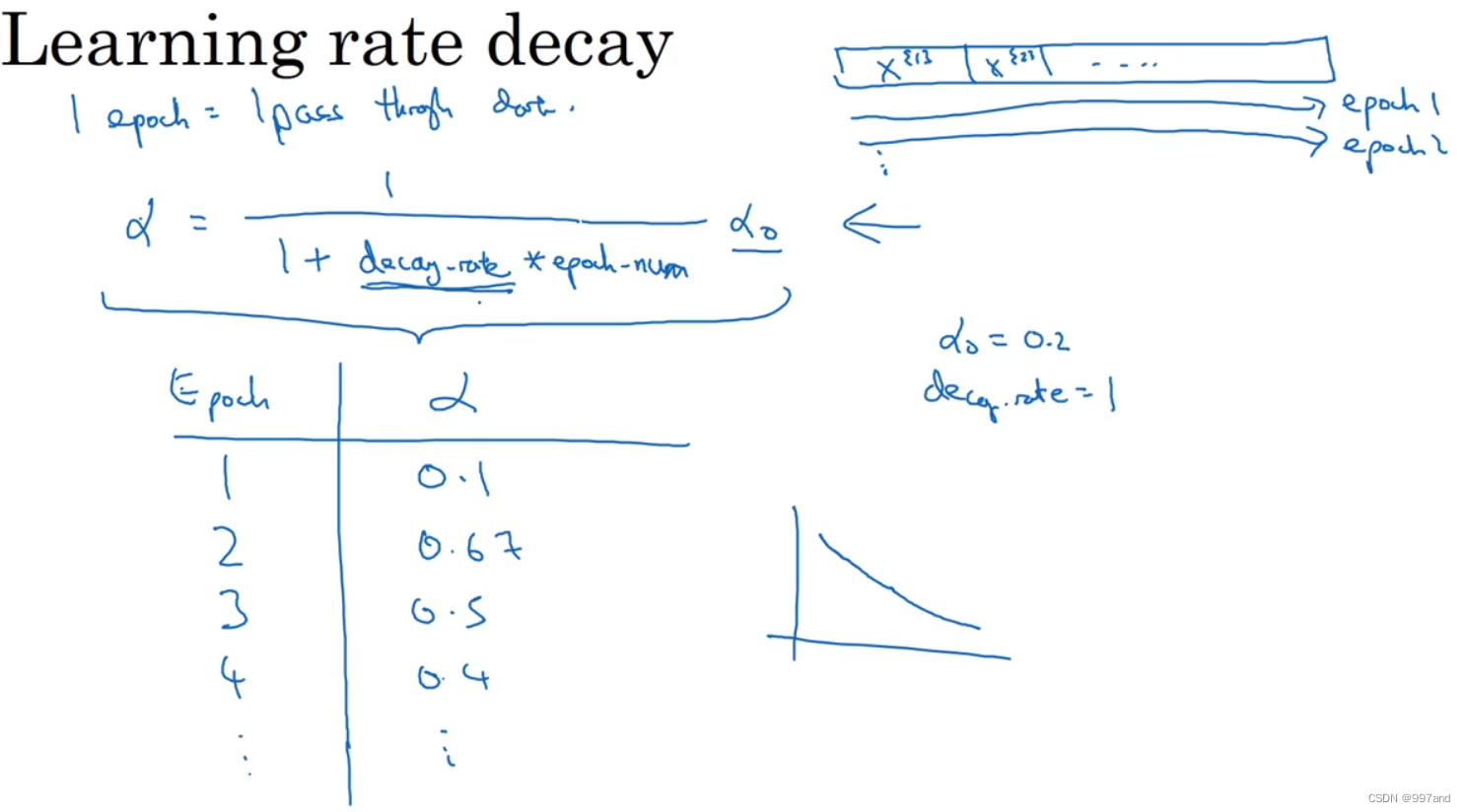
如图右上角数据集,α可设为如图式子,其中decay-rate称为衰减率,epoch-num为代数,α0为初始学习率。
根据图中例子,学习率呈递减趋势。

如图第一个为指数衰减;
第三个离散下降的学习率,即有某个学习率,一会减一半,一会一半。
还有一种是手动衰减,只有模型数量小的时候有用。
十、局部最优的问题(The problem of local optima)
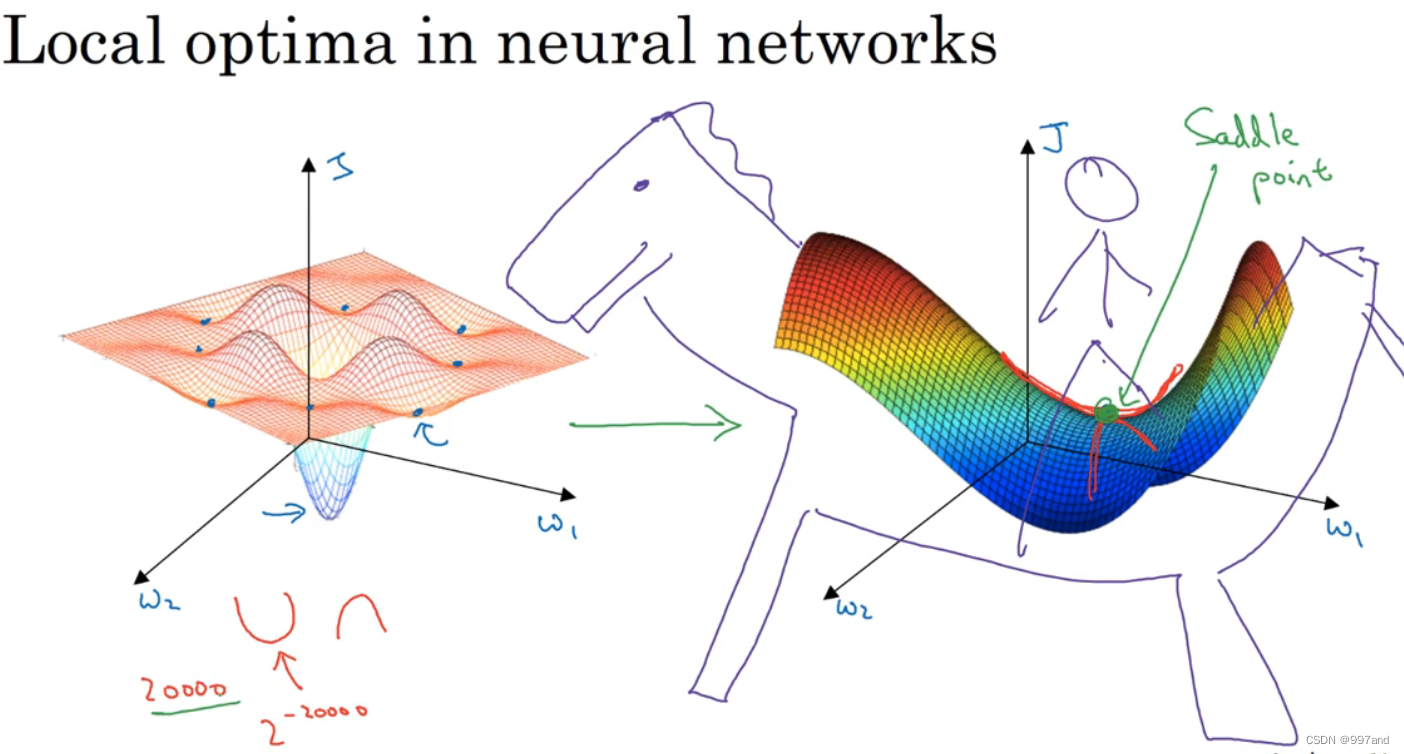
实际上成本函数的零梯度点,通常是鞍点。
但一个具有高维度空间的函数(图右),若梯度为0,那么在每个方向可能是凸函数,也可能是凹函数。高维度空间,更可能碰到鞍点。导数为0称鞍点。
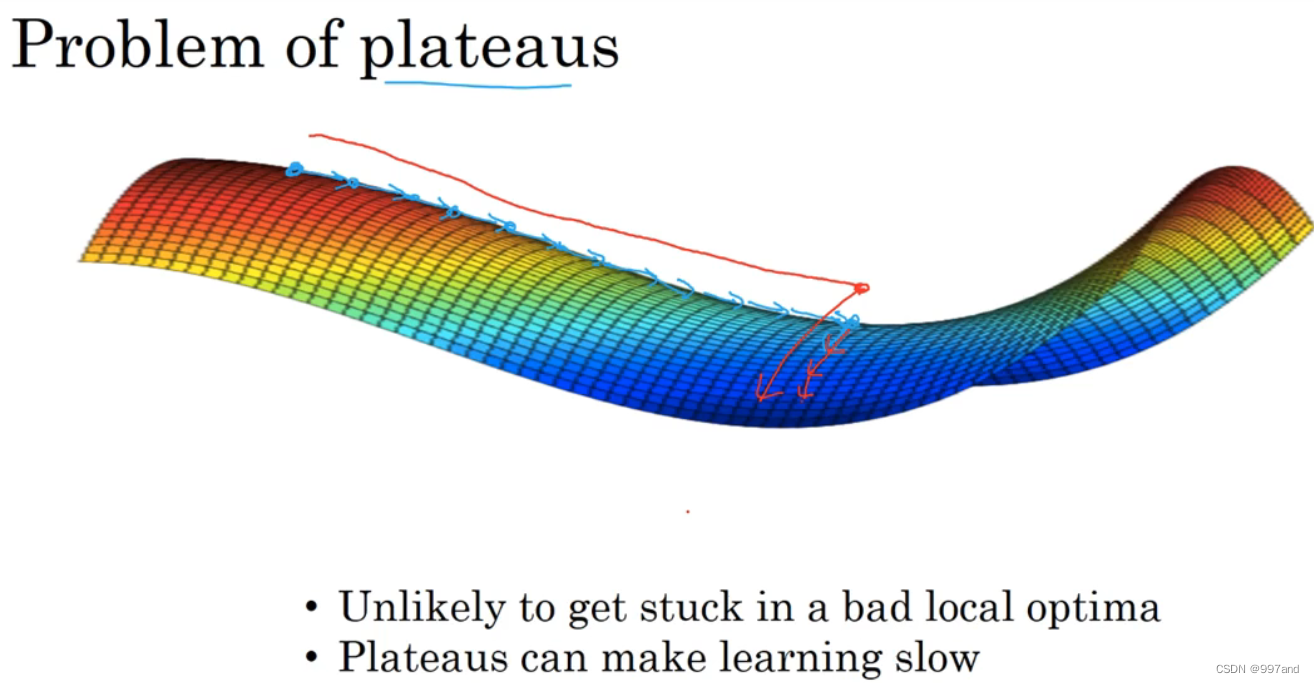
平稳端的导数长时间接近于0。
1.不可能困在极差的局部最优,训练时,存在大量参数,且J被定义在较高维度空间;
2.平稳端使得学习缓慢
