1. 项目背景:
1.1 项目目标:
- 使用提供的波士顿房屋租赁价格数据开发一个模型,该模型可以预测房屋租赁价格,
- 然后解释结果以找到最能预测的变量。
这是一个受监督的回归机器学习任务:给定一组包含目标(在本例中为价格:MEDV)的数据,我们希望训练一个可以学习将特征(也称为解释变量)映射到目标的模型。
- 监督问题: 我们可以知道数据的特征和目标,我们的目标是训练可以学习两者之间映射关系的模型。
- 回归问题: MEDV是一个连续变量。
在训练中,我们希望模型能够学习特征和分数之间的关系,因此我们给出了特征和答案。然后,为了测试模型的学习效果,我们在一个从未见过答案的测试集上进行评估
1.2 工作流程
数据清理和格式化
探索性数据分析
特征工程:数据预处理、特征选择、[特征缩减]
基于性能指标比较几种机器学习模型
对最佳模型执行超参数调整
在测试集上评估最佳模型
解释模型结果
得出结论和报告
1.3 导入库
项目需要的工具
- 使用标准的数据科学和机器学习库:numpy,pandas和sckit-learn
- 使用matplotlib和seaborn进行可视化
- 输入缺失值和缩放值:sklearn.impute,sklearn.preprocessing
- 机器学习模型:
- 把数据分为训练集和测试集:from sklearn.model_selection import train_test_split
- 超参数调整:from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
- 复制对象:copy
- 解释模型:lime
#用于数据操作的pandas和numpy
import numpy as np
import pandas as pd
#设置DataFram显示数量
pd.set_option('display.max_column',60)#最多显示60列
#可视化工具包
import matplotlib.pyplot as plt
import seaborn as sea
# 如遇中文显示问题可加入以下代码
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 复制对象
import copy
from collections import Counter
2. 数据清理和格式化
2.1 加载并检查数据
data_raw=pd.read_csv(r'../data/boston_housing/boston_housing.data')
data_raw
import pandas as pd
df= pd.read_csv(r'../data/boston_housing/boston_housing.data',header=None,sep='\s+')
names = ['CRIM','ZN', 'INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
columns={}
i=0
for li in names:
columns[i]=li
i+=1
data_raw = df.rename(columns=columns)
data_raw.head()
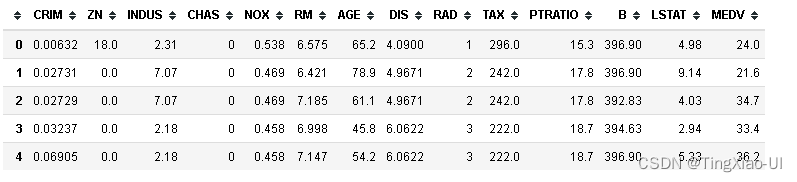
- 存储原始数据到csv
data_raw.to_csv(r'../data/boston_housing/boston_housing.csv',index=False)
data_clean=copy.deepcopy(data_raw)
# 重命名目标变量
data_clean=data_clean.rename(columns={'MEDV':'price'})
加载数据后,我们要解决的第一个问题:理解数据。
我们通常会看到每一列的第一行是各种名词,就是所谓的表头,理解这些名词的含义对于处理数据非常重要,但是我们面对的数据来自各个领域,数据科学家不是精通各个领域专业知识的杂家,这时候就需要通过各种手段去理解数据:
- CRIM:城镇人均犯罪率
- ZN:占地面积超过25,000平方英尺的住宅用地比例
- INDUS:每个城镇非零售业务的比例
- CHAS:Charles River虚拟变量(如果是河道,则为1;否则为0 )
- NOX:一氧化氮浓度(每千万份)
- RM:每间住宅的平均房间数
- AGE:1940年以前建造的自住单位比例
- DIS:波士顿的五个就业中心加权距离
- RAD:径向高速公路的可达性指数
- TAX:每10,000美元的全额物业税率
- PTRATIO:城镇的学生与教师比例
- B:1000(Bk - 0.63)^ 2其中Bk是城镇黑人的比例
- LSTAT:该地区的业主属于是低收入阶层(有工作但收入微薄)所占比例%
- price:自有住房的中位数报价, 单位1000美元,房屋的平均价格
识别特征类型
初步判断:CHAS应为分类变量(如果是河道,则为1;否则为0 ),其他特征均应该为数值型特征。
2.2 数据类型和缺失值
'dataframe.info’方法是一种通过显示每列的数据类型和非缺失值的数量来评估数据的快速方法。注意若某列即存在字符串又存在数字,则意味着带有数字的列将不会表示为数字,营维pandas会将具有任何字符串值的列转换为所有字符串的列
data_clean.info()

- 查看缺失值
def missing_values_table(df):#输入:dataframe数据,输出:缺失总量即比例,降序输出
#计算总的缺失值数量并降序处理
mis_val = df.isnull().sum().sort_values(ascending=False)
mis_val = mis_val[mis_val>0]#提取有缺失值的列
#计算缺失值比例
percent = round(mis_val* 100 /len(df),2)
mis_val_table_ren_columns=pd.concat([mis_val,percent], axis=1, keys=['Missing Values','Percent'])
#打印总结信息:总的列数,有数据缺失的列数
print ("数据集共有 " + str(df.shape[1]) + " 列.\n"+"其中 " + str(mis_val_table_ren_columns.shape[0]) +
" 列有缺失值")
# 返回带有缺失值信息的dataframe
return mis_val_table_ren_columns
#查看缺失值
missing_values_table(data_clean)

- 无缺失值
2.3 检查特征量纲
sea.boxplot(data=data_clean)
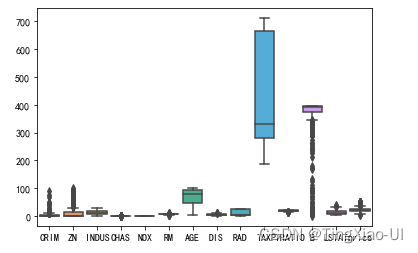
- 部分特征量纲差距大,在训练数前需要特征缩放
2.4 处理重复样本
- 重复样本相当于对某部分样本集合的过采集,从而很可能会提高了这部分样本在全局Loss中所占的比重,模型求解的最终结果会偏向于降低这部分样本的训练误差,而牺牲其他样本的训练误差。
- 重复未必代表冗余,重复的样本也反映了某种信息,某些样本出现的频率比较高,若直接删除可能导致某些模型不准确存在偏差
如何处理重复样本?删除or保留?
- 假设数据采集没有问题:
- 重复数据本身代表了一种真实分布,也就是你的测试集也服从这种分布,那么不该删除,因为这种重复数据表明了某种类型的数据非常重要,出现频率非常高,你的模型该以此类为优先级
- 由于样本各类别重复比例不一定相同,删除重复样本很可能会改变原数据集的分布的,从而影响模型。
- 结合实际业务分析:
- 结合实际业务分析,比如泰坦尼克号数据,有没有特征完全相同的样本(乘客)?姓名、年龄、性别…,本项目选择直接删除重复处理(若存在重复样本)
- 对于回归问题,若重复样本比例比较大,可以选择新增特征列,表示样本出现的次数或者样本是否重复,然后删除重复的样本。
- 检查是否有重复样本
Counter(data_clean.duplicated())
- 数据无重复样本
3. 探索性数据分析
探索性数据分析(EDA)是一个开始式流程,我们制作绘图并计算统计数据,以便探索我们的数据。
- 目的是找到异常,模式,趋势、分布或关系。 例如,找到两个变量之间的相关性,使用哪些特征可用于建模决策。
- 简而言之,EDA的目标是确定我们的数据可以告诉我们什么! EDA通常以高级概述(high-level overview)开始,然后在我们找到要检查的感兴趣的区域时缩小到数据集的特定部分。
要开始EDA,我们将专注于单一变量幸存,因为这是我们的机器学习模型的目标。
通过 describe 和 matplotlib 可视化查看数据各个特征的相关统计量(柱状图)
'data.describe(percentiles=None,include=None,exclude=None)'作用是生成数值特征的描述性统计数据,总结数据集分布的集中趋势,,不包括NaN值。参数含义:
- percentiles:包括在输出中的百分位数。全部应该介于0和1之间。默认值为第25,第50和第75百分位数
- include:默认是None,结果将包括所有数字列
- exclude:默认是None,结果将不包括任何内容。
对于数字数据,则结果将包括count,mean,std,min,max以及第25,第50和第75百分位数,其中第50百分位数等价于中位数。
#统计每列信息
data_clean.describe()
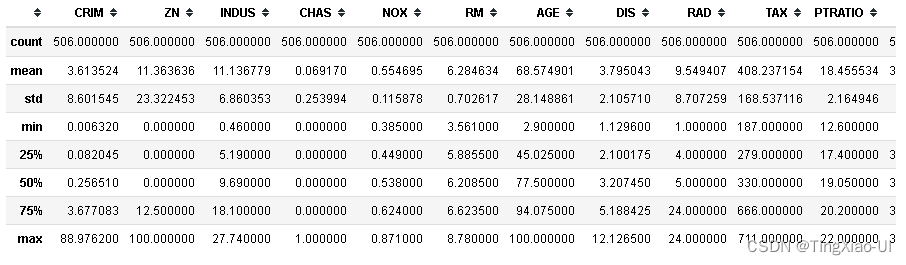
- 可视化查看数据的相关统计量柱状图
data_desc=data_clean.describe().drop('count',axis=0)# 查看数据描述
plt.figure(figsize=(15,5))
i=1
for col in data_desc.columns:
ax=plt.subplot(3,5,i)
ax.set_title(col)
i+=1
for j in data_desc.index:
plt.bar(j,data_desc.loc[j,col])
plt.tight_layout()
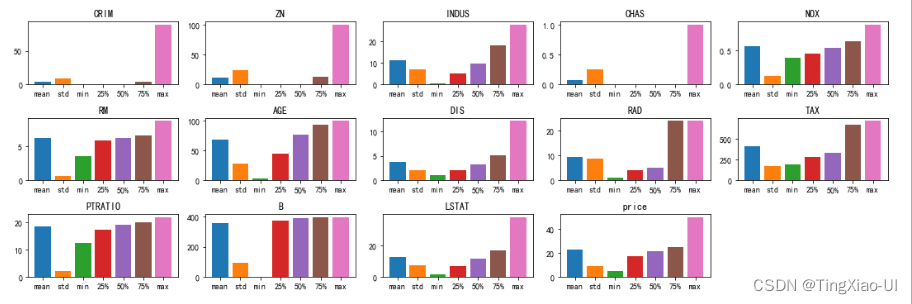
各特征数据分布较为正常,最小值,中位数,最大值是错落分布,正常分布的,且均值和标准差分布也正常。未发现方差极小的特征。
若某个特征方差极小接近于0或者某个特征都是NaN,说明该特征对目标没有什么影响,可以选择直接删除该特征
3.1 查看目标数据的分布情况-单变量图
目的:查看数据失衡程度、检测异常数据
目标是预测price,因此合理的开始是检查目标变量的分布。直方图是可视化单个变量分布的简单而有效的方法,使用matplotlib可以很容易的画出直方图。
fig,ax=plt.subplots(1,2,figsize=(10,5))
sea.histplot(data_clean, x='price',kde=True,ax=ax[0])
# 绘制散点图,查看离散情况
sea.scatterplot(data=data_clean,x=data_clean.index, y='price',ax=ax[1])
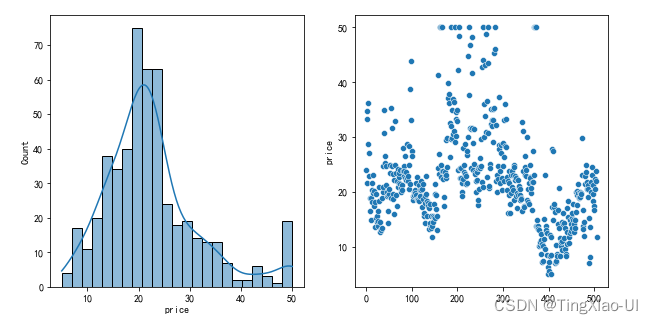
- 目标变量price近似正态分布,右端出现凸起,价格在高端可能有异常值
3.2 检测异常数据
plt.figure(figsize=(15,5))
sea.boxplot(data=data_clean)
- 使用箱线图
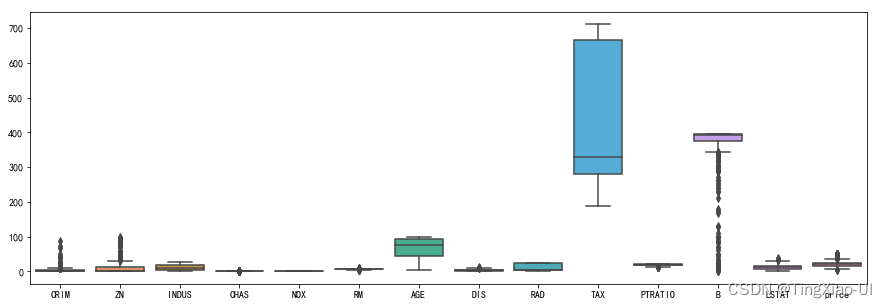
- 使用IQR
q1=data_desc['price']['25%']
q3=data_desc['price']['75%']
iqr=q3-q1
plt.figure(figsize=(15,5))
sea.scatterplot(data=data_clean,x=data_clean.index,y='price')
l=len(data_clean)
plt.plot(data_clean.index,[q1-1.5*iqr]*l,'r')
plt.plot(data_clean.index,[q3+3*iqr]*l,'y')
plt.plot(data_clean.index,[q3+1.5*iqr]*l,'r')
plt.plot(data_clean.index,[q1-3*iqr]*l,'y')
plt.legend(['內限','外限'])
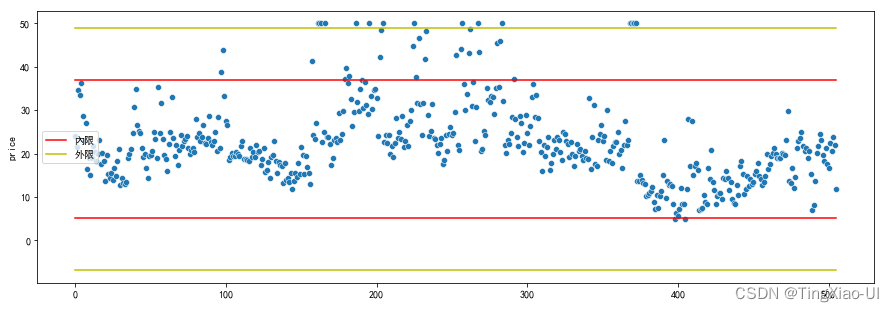
- 使用孤立森林
#使用孤立森林检测多变量异常点
#提取数字特征
data_featrues_num = data_clean
from sklearn.ensemble import IsolationForest
# 创建模型,n_estimators:int,可选(默认值= 100),集合中的基本估计量(树)的数量
model_isof=IsolationForest(n_estimators=100,random_state=123)
# 计算有无异常的标签分布
outlier_label = model_isof.fit_predict(data_featrues_num)#array
# 将array 类型的标签数据转成 DataFrame
outlier_pd = pd.DataFrame(outlier_label, columns=['离群'])
# 将标签数据与原来的数据合并
data_merge = pd.concat([data_featrues_num,outlier_pd], axis=1)
data_merge['离群'].value_counts()
print(data_merge['离群'].value_counts())#-1代表异常点

l=len(data_merge)
plt.figure(figsize=(15,5))
sea.scatterplot(data=data_merge,x=data_clean.index,y='price',hue='离群')
plt.plot(data_clean.index,[q1-1.5*iqr]*l,'r')
plt.plot(data_clean.index,[q3+3*iqr]*l,'y')
plt.plot(data_clean.index,[q3+1.5*iqr]*l,'r')
plt.plot(data_clean.index,[q1-3*iqr]*l,'y')
plt.rcParams['font.sans-serif']=['simhei'] # 指定默认字体
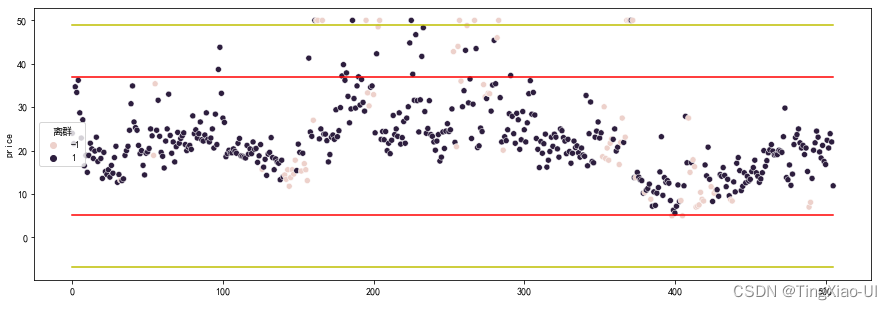
3.2.1 异常点处理
- 提取位于q3+3*iqr外价格的样本
data_outline=data_clean[data_clean['price']>q3+3*iqr]
data_inline=data_clean[data_clean['price']<q3+3*iqr]
data_outline
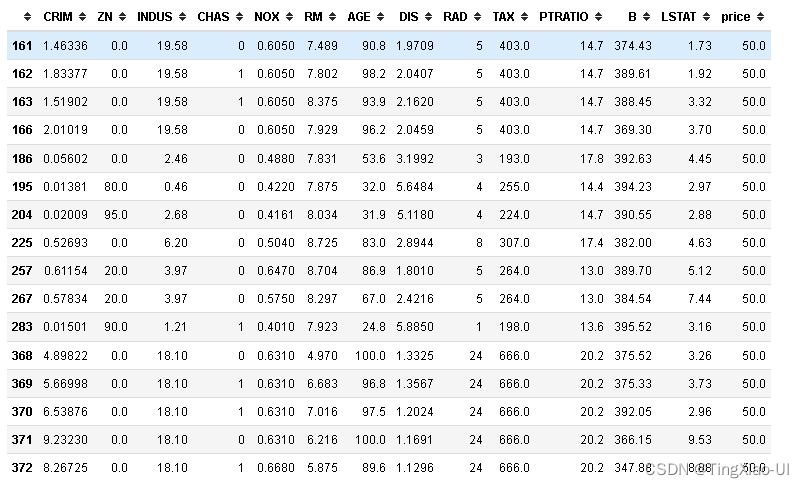
- 使用机器学习模型预测"异常"样本的变量
# 机器学习模型
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.svm import SVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
#评估模型
from sklearn import metrics
#训练集
X_train=np.array(data_inline.drop('price',axis=1))
Y_train=np.array(pd.DataFrame(data_inline['price'])).reshape((-1,))
#"异常"样本
X_test=np.array(data_outline.drop('price',axis=1))
Y_test=np.array(pd.DataFrame(data_outline['price'])).reshape((-1,))
print(X_train.shape,Y_train.shape)
print(X_test.shape,Y_test.shape)
Models=[
LinearRegression(),
RandomForestRegressor(),
GradientBoostingRegressor(),
SVR(),
KNeighborsRegressor(),
MLPRegressor(max_iter=1000)
]
Model_name=['LR','RFR','GB','SVR','KNN','MLPR']
test_mae=[]
for li in Models:
model=GradientBoostingRegressor()
model.fit(X_train,Y_train)
y_pre= model.predict(X_test)
test_mae=test_mae+[metrics.mean_absolute_error(Y_test,y_pre)]
plt.plot(Model_name,test_mae,'*--')
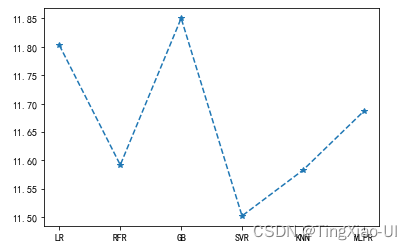
- 移除位于q3+3*iqr外价格的样本
sample_outline=data_clean[data_clean['price']>q3+3*iqr]
data_clean=data_clean[data_clean['price']<q3+3*iqr]
data_clean.shape
- 重置索引
sample_outline=sample_outline.reset_index(drop=True)
data_clean=data_clean.reset_index(drop=True)
3.3 特征分布
- 可以观测到特征的取值范围
- 可以观测到特征不同数值的分布的密度
- 可以观测到特征是连续型还是离散型
# 查看所有数值特征分布
plt.figure(figsize=(15,10))
i=0
for col in data_clean.select_dtypes('number').columns:
i+=1
ax=plt.subplot(3,5,i)
ax.set_title(col)
sea.histplot(data_clean[col],bins=50,kde=True,ax=ax)
plt.tight_layout()#防止文字遮挡
plt.show()
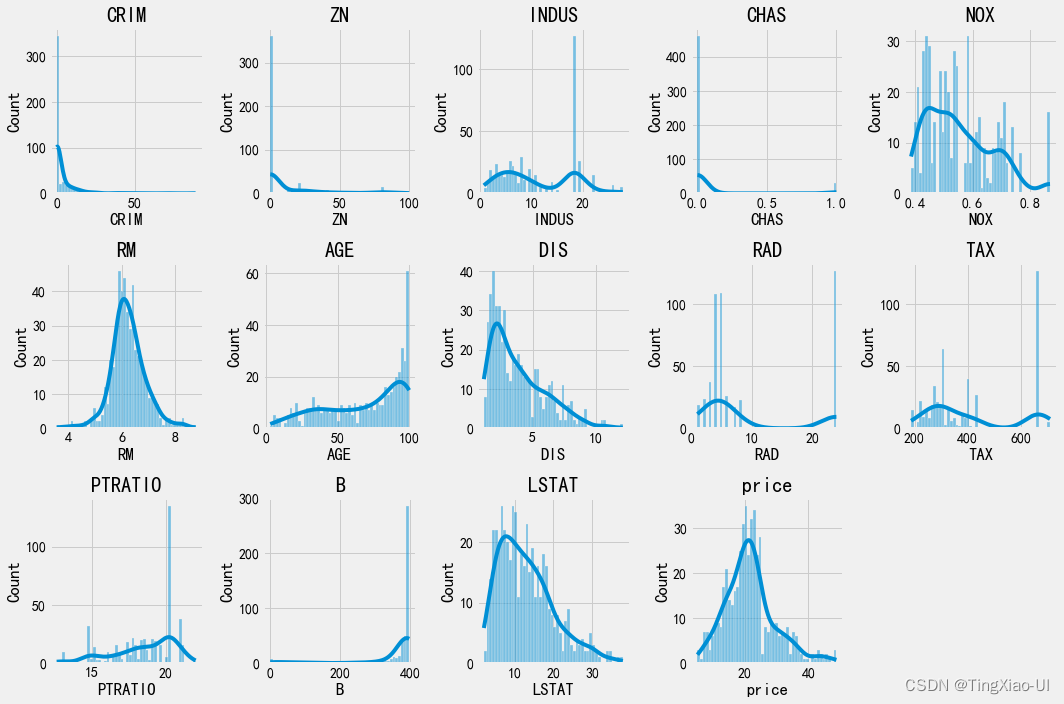
- 查看不同特征去重后数量
#查看不同特征取值数量
lists_unique=[data_clean[col].nunique() for col in data_clean.columns]
#unique():返回去重后的数值,#nunique():返回各数值的计数
# 取值少的可能为类别性数据,取值多的为连续性数据
#绘制柱状图
plt.figure(figsize=(15,5))
plt.bar(data_clean.columns, [data_clean.shape[0]]*data_clean.shape[1]) # 对每个特征绘制总数状图
plt.bar(data_clean.columns, np.array(lists_unique)) # 对每个特征绘制去重数柱状图
plt.ylim(0,30)
plt.title('特征去重值数量')
plt.xlabel('特征')
plt.ylabel('Count')
plt.legend(['总数','去重数'])
plt.tight_layout()#防止文字遮挡
plt.show()
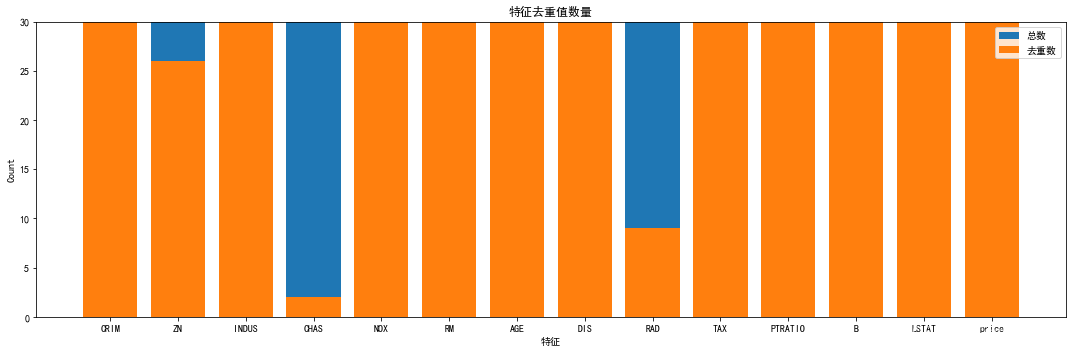
- 特征:CHAS、RAD特征去重值相对很少,可以选择离散化处理
- CHAS:Charles River虚拟变量(如果是河道,则为1;否则为0 )
- RAD:径向高速公路的可达性指数
- ZN:占地面积超过25,000平方英尺的住宅用地比例
lists_unique=[data_clean[col].unique() for col in data_clean[['CHAS','RAD']].columns]
lists_unique
- CHAS转换为分类特征
from pandas.api.types import CategoricalDtype
#转换类型
cat_dtype_chas = CategoricalDtype(categories=[0,1],ordered=False)#ordered:是否为定序类别
data_clean['CHAS']=data_clean['CHAS'].astype(cat_dtype_chas)
data_clean.info()
- 使用决策树对特征RAD、ZN分箱处理
features =data_clean[['RAD','ZN']]
target = data_clean['price']
data_cuts=decTreeBin(features,target,max_depth=2,model='Regressor')
data_clean=pd.concat([data_clean.drop(['RAD','ZN','price'],axis=1),data_cuts,target],axis=1)
data_clean.head()
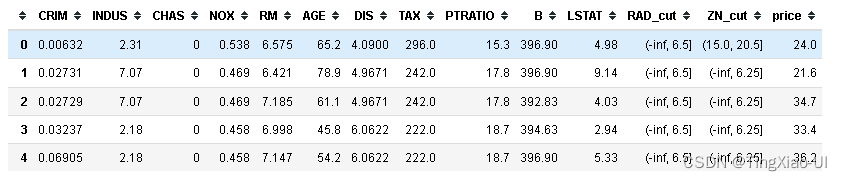
3.3.1评估分箱效果
- 查看分类变量与目标关系
为了查看分类变量对目标的影响,我们可以通过分类变量的值来绘制密度图。
密度图还显示单个变量的分布,可以认为是平滑的直方图。 如果我们通过为分类变量密度曲线着色,这将向我们展示分布如何基于类别变化的。
对于包含较多分类的变量,为了不使图形混乱,可选取数量超过指定阈值的分类来绘图
data_clean.select_dtypes('category').info()

plt.figure(figsize=(15,5))
#查看RAD_cut分类变量与目标的关系
plt.subplot(1,3,1)
RAD_list=data_clean['RAD_cut'].unique()
for li in RAD_list:
subest = data_clean[data_clean['RAD_cut']==li]
sea.kdeplot(data=subest['price'])
plt.legend(RAD_list)
#查看CHAS分类变量与目标的关系
plt.subplot(1,3,2)
CHAS_list=data_clean['CHAS'].unique()
for li in CHAS_list:
subest = data_clean[data_clean['CHAS']==li]
sea.kdeplot(data=subest['price'])
plt.legend(CHAS_list)
#查看ZN分类变量与目标的关系
plt.subplot(1,3,3)
ZN_list=data_clean['ZN_cut'].unique()
for li in ZN_list:
subest = data_clean[data_clean['ZN_cut']==li]
sea.kdeplot(data=subest['price'])
plt.legend(ZN_list)
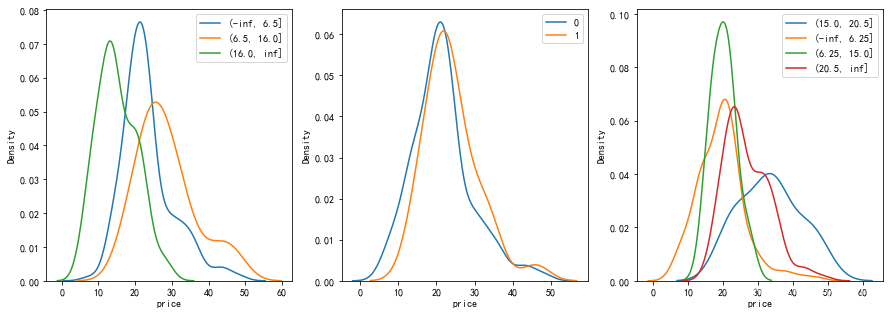
- 不同RAD区间对目标变量有一定影响,RAD∈(16,inf]的房屋价格偏低,RAD∈(6.5,16]的房屋价格较高
- CHAS分类变量对目标变量影响不大
3.4 寻找关系
3.4.1特征与目标的相关性
为了量化特征(变量)和目标之间的相关性,我们可以计算Pearson相关系数。 这是两个变量之间线性关系的强度和方向的度量:
- - 1 表示两个变量完全负线性相关,
- +1 表示两个变量完全正线性相关。
注意:
- 特征和目标之间可能存在非线性关系,
线性关系是开始探索数据趋势的好方法。 然后,我们可以使用这些值来选择要在我们的模型中使用的特征。
计算特征(变量)与目标之间的相关系数前首先要对分类特征做one_hot编码
# 对分类变量做one-hot编码
categorical_features=pd.get_dummies(data_clean.select_dtypes('category'))
data_clean=pd.concat([data_clean.drop(['price','CHAS','RAD_cut'],axis=1),categorical_features,data_clean['price']],axis=1)
data_clean.info()
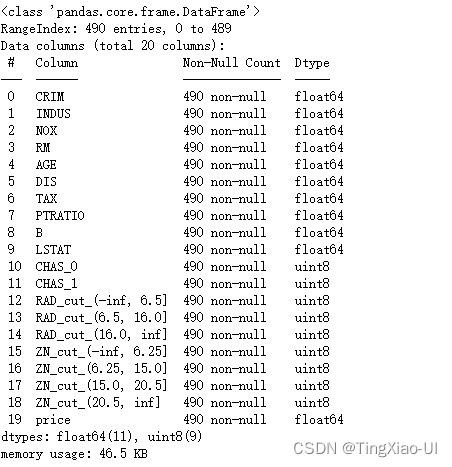
3.4.2 查看特征与特征、与目标的相关性
我们可以在几个不同的变量之间建立Pairs Plot。 Pairs Plot是一次检查多个变量的好方法,因为它显示了对角线上的变量对和单个变量直方图之间的散点图。
使用seaborn PairGrid函数,我们可以将不同的图绘制到网格的三个方面:
- 上三角显示散点图
- 对角线将显示直方图
- 下三角形将显示两个变量之间的相关系数和两个变量的2-D核密度估计。
# 计算某两列之间的相关系数
def corr_func(x,y,**kwargs):
r = np.corrcoef(x,y)[0][1]
ax = plt.gca()
ax.annotate("r = {:.2f}".format(r),
xy = (.2,.8),
xycoords = ax.transAxes,
size = 20)
grid= sea.PairGrid(data_clean.iloc[:,:10])
# 在对角线上的坐标轴内画图
grid.map_diag(sea.histplot)
# 在非对角线上的坐标轴内画图
# grid.map_offdiag(sea.kdeplot, n_levels=6)
#在上三角绘制散点图
grid.map_upper(sea.scatterplot)
# 在下三角绘制核密度图+相关系数
grid.map_lower(sea.kdeplot,cmap = plt.cm.Reds)
grid.map_lower(corr_func)
3.5 特征变换
为了考虑可能的非线性关系,我们可以采用如下变换,然后分别计算变换后的特征与目标的相关系数,选取相关系数最大特征变换方式:
- 特征的平方根和自然对数变换,然后用得分计算相关系数
- 指数和幂变换,然后用得分计算相关系数
qq=Sift(data_clean.select_dtypes('number'),'price')
qq.fit()
data_corr=qq.corr
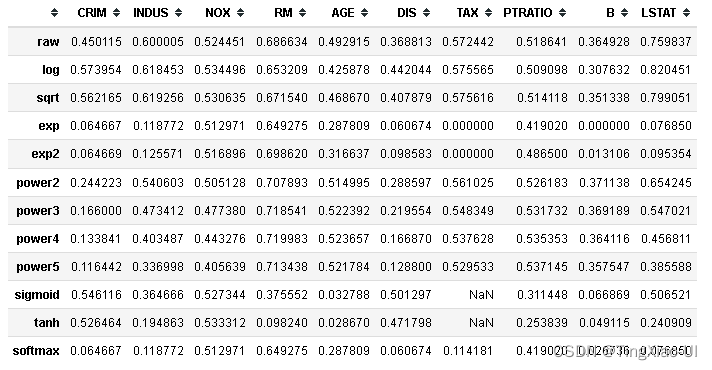
plt.figure(figsize=(15,5))
sea.lineplot(data=data_corr.iloc[:,:5],dashes=False)
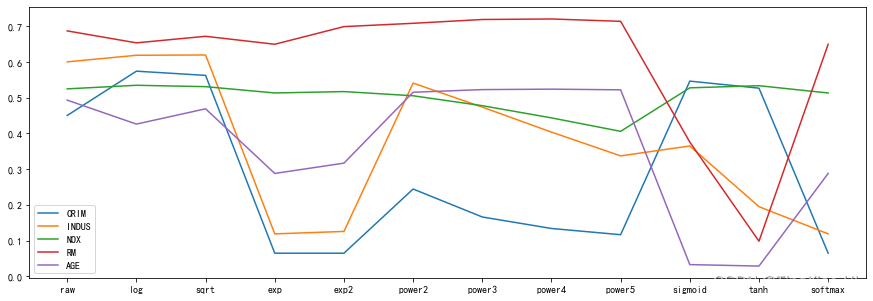
qq.select

最佳特征变换
- CRIM:采用对数变换
- INDUS:采用sqrt变换
- NOX:采用对数变换
- RM:采用幂变换-4
- AGE:采用幂变换-4
- DIS:采用sigmoid变换
- TAX:采用sqrt变换
- PTRATIO:采用幂变换-5
- B:采用幂变换-2
- LSTAT:采用对数变换
features_number =data_clean.drop('price',axis=1).select_dtypes('number')
features_category=data_clean.select_dtypes('category')
features_number['log_CRIM']=np.log(features_number['CRIM'])
features_number['sqrt_INDUS']=np.sqrt(features_number['INDUS'])
features_number['log_NOX']=np.log(features_number['NOX'])
features_number['4_RM']=np.power(features_number['RM'],4)
features_number['sigmoid_DIS']=1/(1+np.exp(-features_number['DIS']))
features_number['sqrt_TAX']=np.sqrt(features_number['TAX'])
features_number['5_PTRATIO']=np.power(features_number['PTRATIO'],5)
features_number['2_B']=np.power(features_number['B'],2)
features_number['log_LSTAT']=np.log(features_number['LSTAT'])
# 用 nan 替换 inf and -inf
# features_number = features_number.replace({np.inf: np.nan, -np.inf: np.nan})
- 检查新增特征后是否有缺失值、inf
missing_values_table(features_number)

np.isfinite(features_number).sum().value_counts()
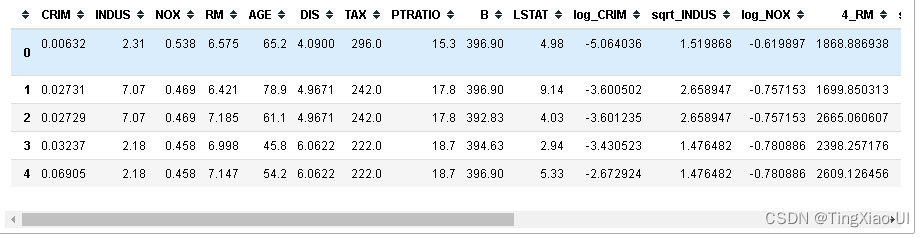
- 组合特征
data_select=pd.concat([features_number,features_category,data_clean.price],axis=1)
data_select.head()
4. 特征工程
现在我们已经台探索了数据中的趋势和关系,我们可以使用EDA的结果来构建特征工程。我们从EDA学到了以下知识,可以帮助我们进行特征工程:
问题类型:回归、监督学习问题,
- 目标字段:price
- 无缺失值、重复值
- 移除"异常"数据:移除price为50的样本
- CHAS转换为分类特征、RAD分箱
- 新增特征:
- CRIM:采用对数变换
- INDUS:采用sqrt变换
- NOX:采用对数变换
- RM:采用幂变换-4
- AGE:采用幂变换-4
- DIS:采用sigmoid变换
- TAX:采用sqrt变换
- PTRATIO:采用幂变换-5
- B:采用幂变换-2
- LSTAT:采用对数变换
在此项目中,我们将采用以下步骤进行特征工程:
数据预处理:
- 移除price为50的样本,重置索引
- CHAS转换为分类特征、RAD分箱;
- 新增特征:
- 分类特征做one_hot编码
分割数据集:训练集+测试集
特征缩放
特征选择:保留有价值特征,删除无关特征和冗余特征(共线特征)
4.1 数据预处理
#复制数据
data_clean = copy.deepcopy(data_raw)
data_clean=copy.deepcopy(data_raw)
# 重命名目标变量
data_clean=data_clean.rename(columns={'MEDV':'price'})
data_clean.head()
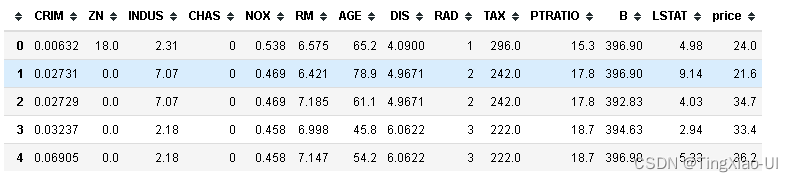
4.1.1处理异常样本
- 移除price为50的样本,重置索引
data_desc=data_clean.describe().drop('count',axis=0)# 查看数据描述
q1=data_desc['price']['25%']
q3=data_desc['price']['75%']
iqr=q3-q1
#移除位于q3+3*iqr外价格的样本
sample_outline=data_clean[data_clean['price']>q3+3*iqr]
data_clean=data_clean[data_clean['price']<q3+3*iqr]
#重置索引
sample_outline=sample_outline.reset_index(drop=True)
data_clean=data_clean.reset_index(drop=True)
data_clean.shape
4.1.2 转换类型+分箱
- CHAS转换为分类特征
from pandas.api.types import CategoricalDtype
#转换类型
cat_dtype_chas = CategoricalDtype(categories=[0,1],ordered=False)#ordered:是否为定序类别
data_clean['CHAS']=data_clean['CHAS'].astype(cat_dtype_chas)
- RAD、ZN分箱
features =data_clean[['RAD','ZN']]
target = data_clean['price']
data_cuts=decTreeBin(features,target,max_depth=2,model='Regressor')
data_clean=pd.concat([data_clean.drop(['RAD','ZN','price'],axis=1),data_cuts,target],axis=1)
data_clean.head()
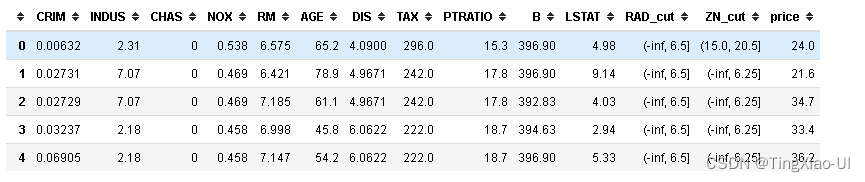
data_clean.info()

4.1.3 新增特征
- CRIM:采用对数变换
- INDUS:采用sqrt变换
- NOX:采用对数变换
- RM:采用幂变换-4
- AGE:采用幂变换-4
- DIS:采用sigmoid变换
- TAX:采用sqrt变换
- PTRATIO:采用幂变换-5
- B:采用幂变换-2
- LSTAT:采用对数变换
#提取数值特征
features_number =data_clean.drop('price',axis=1).select_dtypes('number')
#提取分类特征
features_category=data_clean.select_dtypes('category')
#特征变换
features_number['log_CRIM']=np.log(features_number['CRIM'])
features_number['sqrt_INDUS']=np.sqrt(features_number['INDUS'])
features_number['log_NOX']=np.log(features_number['NOX'])
features_number['4_AGE']=np.power(features_number['AGE'],4)
features_number['4_RM']=np.power(features_number['RM'],4)
features_number['sigmoid_DIS']=1/(1+np.exp(-features_number['DIS']))
features_number['sqrt_TAX']=np.sqrt(features_number['TAX'])
features_number['6_PTRATIO']=np.power(features_number['PTRATIO'],6)
features_number['2_B']=np.power(features_number['B'],2)
features_number['log_LSTAT']=np.log(features_number['LSTAT'])
# 用 nan 替换 inf and -inf
# features_number = features_number.replace({np.inf: np.nan, -np.inf: np.nan})
4.1.4 分类特征做one_hot编码
#对分类变量做one-hot编码
features_category=pd.get_dummies(features_category)
- 组合特征
data_select=pd.concat([features_number,features_category,data_clean.price],axis=1)
data_select.head()
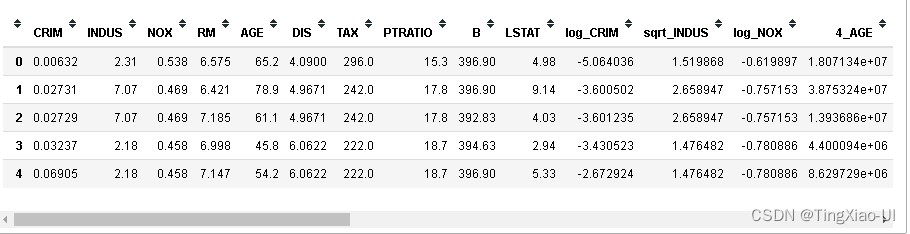
data_select.shape

4.2 特征选择
4.2.1 查看特征与特征、目标的相关性
plt.figure(figsize=(30,15))
data_corr = data_select.corr().abs()
sea.heatmap(data_corr,annot=True,cmap='coolwarm',linewidths=.5)
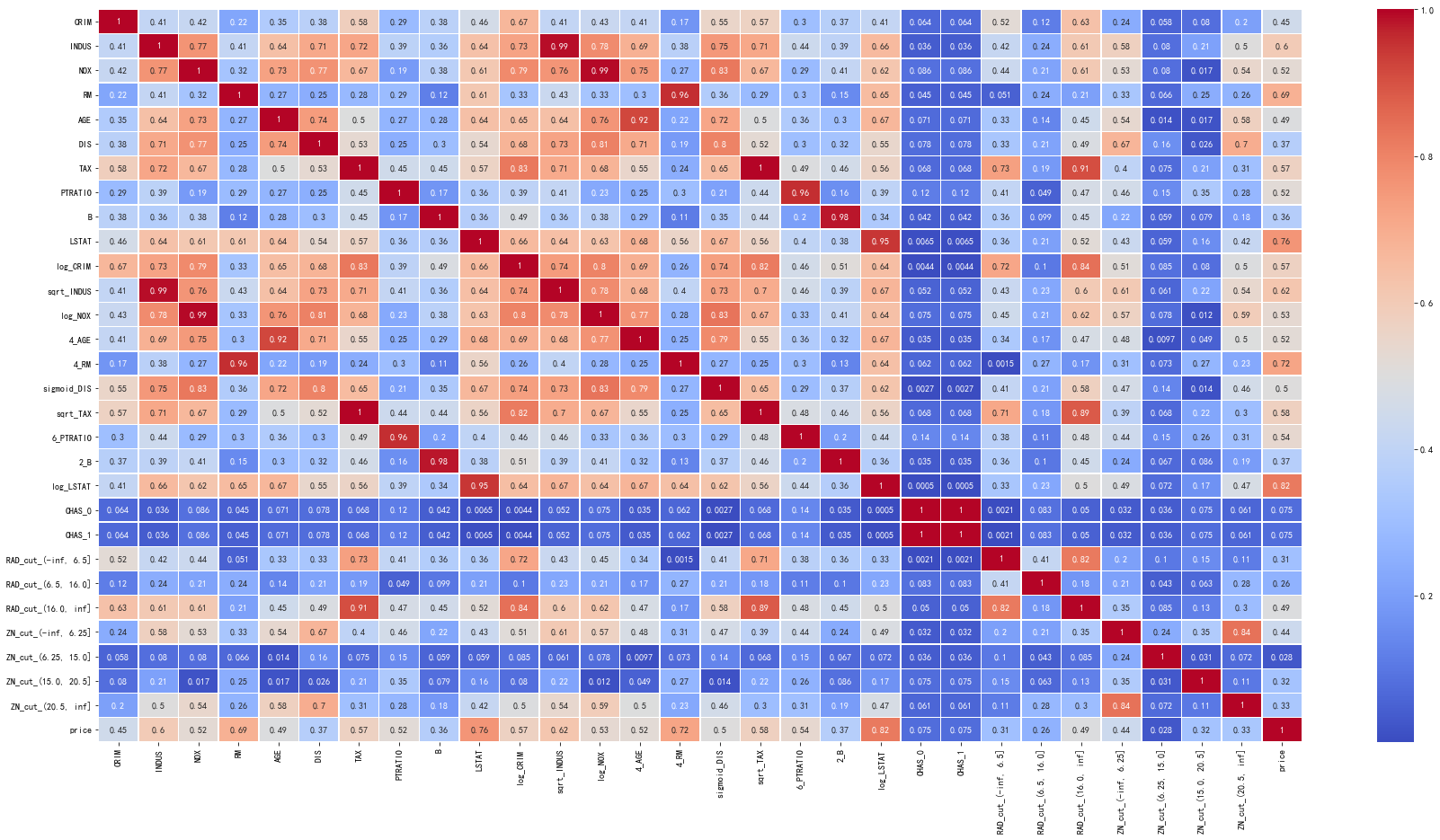
4.2.2 过滤冗余特征
- 过滤相关性大于指定阈值的特征
#删除相似特征:根据特征与特征的相关性大小以及特征与目标的相关性高低做判断是删除i还是j
def delCorrFeatrue(inx,iny,th):#inx:特征,dataframe,target:目标变量名称,dataframeth:阈值
#特征与目标相关性
data = pd.concat([inx,iny],axis=1)
data_corr = data.corr().abs()[iny.columns[0]]
#特征与特征相关性
cols = inx.columns # 获取特征列的名称
corr_list = []
size = inx.shape[1]
high_corr_fea = [] # 存储相关系数大于0.6的特征名称
features_corr = inx.corr().abs()
#筛选高于阈值的特征
for i in range(0,size):
for j in range(i+1, size):
if(abs(features_corr.iloc[i,j])>= th):
corr_list.append([features_corr.iloc[i,j], i, j]) # features_corr.iloc[i,j]:按位置选取数据
sorted_corr_list = sorted(corr_list, key=lambda xx:-abs(xx[0]))
#遍历列表
for v,i,j in sorted_corr_list:#根据特征与目标的相关性高低做判断是删除i还是j
if data_corr[cols[i]]>=data_corr[cols[j]]:
high_corr_fea.append(cols[j])
else:
high_corr_fea.append(cols[i])
#列表去重
high_corr_fea = list(set(high_corr_fea))
# 删除特征
#inx.drop(labels=high_corr_fea,axis=1,inplace=True)
inx = inx.drop(high_corr_fea,axis=1)
return inx
features=data_select.drop(['price'],axis=1)
target = data_select[['price']]
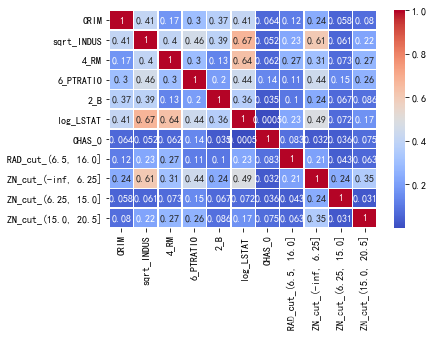
# 删除大于指定相关系数的共线特征
features = delCorrFeatrue(features,target, 0.7)
#绘制相关系数图
data_corr = features.corr().abs()
sea.heatmap(data_corr,annot=True,cmap='coolwarm',linewidths=.5)
#组合特征
data_select=pd.concat([features,target],axis=1)
#绘制相关系数图
data_corr = data_select.corr().abs()
sea.heatmap(data_corr,annot=True,cmap='coolwarm',linewidths=.5)
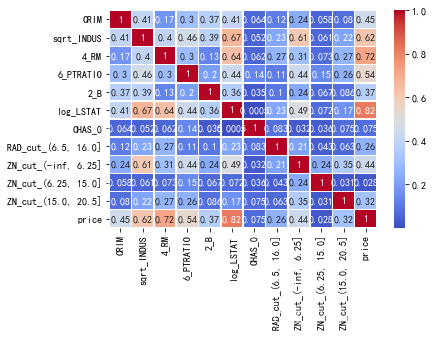
4.2.3 过滤无关特征
#删除无关特征
def delUselessFeatrue(inx,target,th):#inx包括目标变量,dataframe,target:目标变量名称,th:阈值
data = copy.deepcopy(inx)
#计算相关系数
corr_df = data.corr().abs()[target].sort_values()
corr_df = pd.DataFrame(corr_df)
# 提取大于th的特征
indexs = corr_df[corr_df[target]>=th].index
data = data[indexs]
return data
data_select.shape

data_select=delUselessFeatrue(data_select,'price',0.1)
data_select.info()
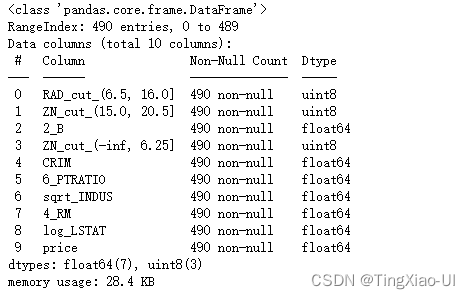
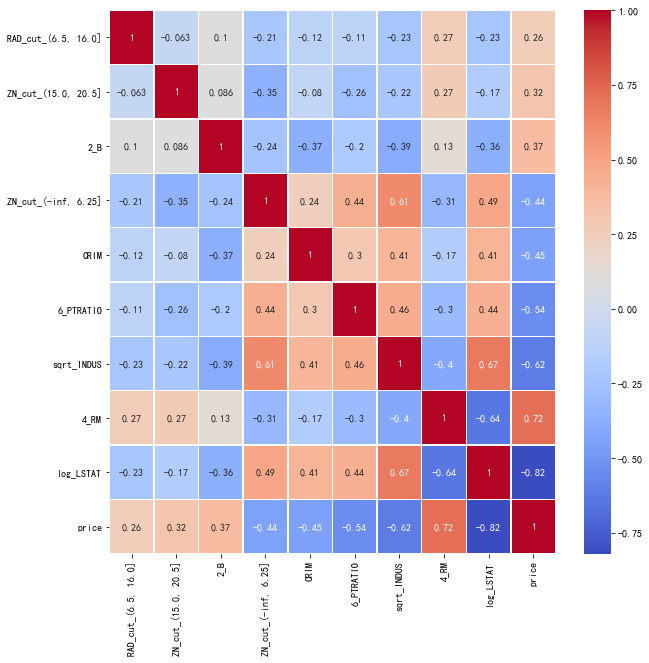
#绘制相关系数图
data_corr = data_select.corr()
plt.figure(figsize=(10,10))
sea.heatmap(data_corr,annot=True,cmap='coolwarm',linewidths=.5)
4.3 划分数据集为训练集和测试集
- 检查数据目前是否有缺失值、inf
missing_values_table(data_select)

np.isfinite(data_select).sum().value_counts()

# 把数据分为训练集和测试集
from sklearn.model_selection import train_test_split
features = data_select.drop(['price'],axis=1)
target = data_select[['price']]
# 按照7:3比例划分,并且划分后的类别分布比例保持一致
# stratify=targets,用来确保划分后的类别分布比例保持一致
#shuffle=True,表示打乱数据
x_train,x_test,y_train,y_test = train_test_split(features,target,test_size=0.2,random_state=123,shuffle=True)
print('训练集:',x_train.shape,'测试集:',x_test.shape)

4.4 特征缩放
- 使用自定义归一化函数做特征缩放
def scalerMm(inx,model='min'):#inx:特征类型为数值特征
base = copy.deepcopy(inx)
for col in base.columns:
#排除非数值类型的列
if str(base[col].dtypes) != 'category' and str(base[col].dtypes) != 'object':
# print(col,base[col].dtypes)
value_max = np.max(base[col])
value_min = np.min(base[col])
scale = value_max-value_min
if model=='min':
base[col] = (base[col]-value_min)/scale
elif model=='mean':
value_mean = np.mean(base[col])
base[col] = (base[col]-value_mean)/scale
# print(value_mean)
return base
#1. 训练集做特征缩放
x_train = scalerMm(x_train)#DataFrame,m*n
#2. 测试集做特征缩放
x_test = scalerMm(x_test)#DataFrame,m*n
4.4.1 保存数据
如果需要保存已经处理好的数据集可以用下面的代码:
x保存为training_features.csvx_test保存为testing_features.csvy保存为training_labels.csvy_test保存为testing_labels.csv
#保存数据
x_train.to_csv(r'../data/boston_housing/train_features.csv',index=False)#index=False,excel不添加索引
y_train.to_csv(r'../data/boston_housing/train_laels.csv',index=False)
x_test.to_csv(r'../data/boston_housing/test_features.csv',index=False)
y_test.to_csv(r'../data/boston_housing/test_laels.csv',index=False)
5 建模、预测和解决问题
5.1 需要评估的模型
有多种预测建模算法可供选择。我们必须了解问题的类型和解决方案的需求,将范围缩小到我们可以评估的少数几个模型。我们的问题是一个回归问题,我们想要确定输出(房屋租赁价格)与其他变量或特征之间的关系。当我们用给定的数据集训练我们的模型时,我们也在进行一类被称为监督学习的机器学习。有了这两个标准(监督学习、回归),我们可以缩小我们的模型选择,包括:
- 线性回归:
- 普通最小二乘法回归
- 岭回归:线性最小二乘法、L2范数正则化
- 核岭回归:线性最小二乘法、L2范数正则化与核技巧相结合
- Lasso回归:线性最小二乘法、L1范数正则化
- 弹性网络回归:线性最小二乘法、L1范数正则化、L2范数正则化
- 逐步回归
- 广义线性回归
- 贝叶斯回归
- 分位数回归
- 支持向量机回归
- K近邻回归
- 决策树回归
- 随机森林回归
- 梯度提升回归
- 导入库
# 机器学习模型
#******线性模型**********
from sklearn.linear_model import LinearRegression#普通最小二乘法线性回归
from sklearn.linear_model import Ridge#岭回归
from sklearn.linear_model import Lasso#Lasso回归
from sklearn.linear_model import ElasticNet#弹性网络回归
from sklearn.linear_model import BayesianRidge# 贝叶斯回归
from sklearn.linear_model import QuantileRegressor#分位数回归
from sklearn.kernel_ridge import KernelRidge# 内核岭回归
#********树模型*****************
from sklearn.tree import DecisionTreeRegressor#决策树回归
from sklearn.tree import ExtraTreeRegressor#极限树回归
from sklearn.ensemble import RandomForestRegressor#随机森林回归
from sklearn.ensemble import GradientBoostingRegressor#梯度提升回归
#***********集成算法************
from sklearn.ensemble import AdaBoostRegressor#AdaBoost回归
from sklearn.ensemble import BaggingRegressor#Bagging回归
#***********
from sklearn.neighbors import KNeighborsRegressor#KNN回归
from sklearn.svm import SVR#支持向量回归
from sklearn.neural_network import MLPRegressor#多层感知机回归
# 超参数调整
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
#评估分类性能
from sklearn import metrics
from sklearn.model_selection import cross_val_score #score evaluation
#绘制学习曲线、验证曲线
from sklearn.model_selection import learning_curve,validation_curve
- 读取数据并格式化处理
train_features = pd.read_csv(r'../data/boston_housing/train_features.csv')
train_labels = pd.read_csv(r'../data/boston_housing/train_laels.csv')
test_features = pd.read_csv(r'../data/boston_housing/test_features.csv')
test_labels = pd.read_csv(r'../data/boston_housing/test_laels.csv')
print('Training Feature Size: ', train_features.shape)
print('Testing Feature Size: ', test_features.shape)
print('Training Labels Size: ', train_labels.shape)
print('Testing Labels Size: ', test_labels.shape)
# X_train= np.array(train_features)#m*n
# Y_train = np.array(train_labels).reshape((-1, ))#m
#转换数据为array格式
X_test=np.array(test_features)#m*n
Y_test = np.array(test_labels).reshape((-1, ))#m
X_train= np.array(train_features)#m*n
Y_train = np.array(train_labels).reshape((-1, ))#m
5.2 建立Baseline
在我们开始制作机器学习模型之前建立一个基线是很重要的。
- 如果我们构建的模型不能胜过基线,那么我们可能不得不承认机器学习不适合这个问题。 这可能是
- 因为我们没有使用正确的模型,
- 因为我们需要更多的数据,
- 或者因为有一个更简单的解决方案不需要机器学习。
建立基线至关重要,因此我们最终可能不会构建机器学习模型,只是意识到我们无法真正解决问题。
- 对于回归任务,一个好的基线是为测试集上的所有实例预测目标在训练集上的中值。 这很容易实现,并为我们的模型设置了相对较低的标准:如果它们不能比猜测中值更好,那么我们需要重新考虑我们的方法。
- 对于分类任务,选取一种机器学习模型,使用默认超参数参数以及评分标准,使用分层交叉验证评估模型选取平均分
1. 对于二元分类,计算AUC: * y_true = Y_train#n_samples * y_score=Y_pre#n_samples,预测值 * metrics.roc_auc_score(y_true,y_score,average='macro/weighted') * * cross_val_score(model, X_train, Y_train, scoring='roc_auc', cv=5).mean() 2. 对于多类,计算AUC * classes = np.unique(Y_train) * y_true=label_binarize(Y_train, classes=classes) #装换成类似二进制的编码,n_samples*n_classes * Y_pre=model.predict_proba(X_train)#n_samples*n_classes,各个类别的预测概率 * metrics.roc_auc_score(y_true,y_score,average='macro/weighted',multi_class='ovr/ovo',labels=classes) * * cross_val_score(model, X_train, y=Y_train, scoring='roc_auc_ovr_weighted', cv=5).mean()
cross_val_score和metrics得到的score可能会差很多,cross_val_score是多次交叉验证得到的评分而metrics是基于单次预测结果得到的评分。
# 使用中位数预测结果
baseline_guess =np.array([np.median(Y_train)]*len(Y_train)).reshape((-1,))
#Baselinep评分:r2_score
baseline_score=metrics.r2_score(Y_train,baseline_guess)
print(baseline_score)
5.3 模型评估与选择
models=[
LinearRegression(),
Ridge(random_state=123),
Lasso(random_state=123),
ElasticNet(random_state=123),
BayesianRidge(),
QuantileRegressor(),
KernelRidge(),
DecisionTreeRegressor(random_state=123),
ExtraTreeRegressor(random_state=123),
RandomForestRegressor(random_state=123),
GradientBoostingRegressor(random_state=123),
AdaBoostRegressor(random_state=123),
BaggingRegressor(random_state=123),
KNeighborsRegressor(),
SVR(),
MLPRegressor(random_state=123,max_iter=10000)
]
model_name=[
'普通最小二乘法线性回归',
'岭回归',
'Lasso回归',
'弹性网络回归',
'贝叶斯回归',
'分位数回归',
'核岭回归',
'决策树回归',
'极限树回归',
'随机森林回归',
'梯度提升回归',
'AdaBoost回归',
'Bagging回归',
'KNN回归',
'支持向量回归',
'多层感知机回归'
]
# Scores={a:b for a,b in zip(model_name,np.zeros(len(model_name)))}
Scores={}
Scores['Model']=model_name
Scores['train_Score']=np.zeros(len(model_name))
Scores['test_Score']=np.zeros(len(model_name))
Scores

for i,mo in enumerate(models):#逐个训练每个模型并评估
model_name=Scores['Model'][i]
print('模型:',model_name)
#训练集评分
Scores['train_Score'][i]=round(cross_val_score(mo,X_train,Y_train, scoring='r2', cv=5).mean(),3)#neg_mean_absolute_error、r2
#测试集评分
model=mo.fit(X_train,Y_train)
Y_pre=model.predict(X_test)
# Scores['test_Score'][i]=metrics.mean_absolute_error(Y_test,Y_pre)
Scores['test_Score'][i]=metrics.r2_score(Y_test,Y_pre)
- 可视化评分
data_plot=pd.DataFrame(Scores)
index=data_plot.sort_values(by='train_Score', ascending=True).index
data_plot=data_plot.loc[index,:]
plt.figure(figsize=(15,8))
plt.barh(data_plot.Model,data_plot.train_Score) # 对每个特征绘制总数状图
# plt.barh(data_plot.Model,data_plot.调和平均,alpha=1)
plt.barh(data_plot.Model,data_plot.test_Score)
# sea.set_color_codes("pastel")
# sea.barplot(data=data_plot,x='train_Score',y='Model',color='b')
# sea.set_color_codes("muted")
# sea.barplot(data=data_plot,x='调和平均',y='Model',color='y')
# sea.barplot(data=data_plot,x='test_Score',y='Model',color='r')
plt.xlabel('R2_Score')
plt.legend(['train_R2','test_R2'])
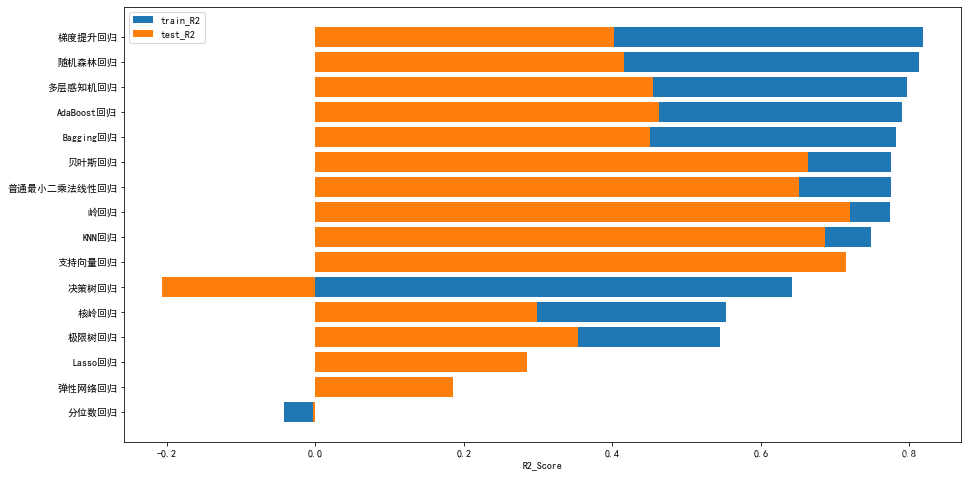
模型初步测试:梯度提升回归训练集表现最优但泛化能力较差。本例将对梯度提升回归调整超参数
5.4 模型调整超参数
5.4.1 梯度提升回归调整超参数
5.4.1.1使用随机搜索和交叉验证进行超参数调整
梯度提升回归超参数选项
我们选择了7个不同的超参数来调整梯度提升回归。 这些都将以不同的方式影响模型,这些方法很难提前确定,找到特定问题的最佳组合的唯一方法是测试它们!
#损失函数:squared_error:平方误差,absolute_error:绝对误差,huber:二者混合,quantile:分位数
loss=['squared_error','absolute_error', 'huber', 'quantile']
#树数量
n_estimators=[100,200,500,700, 900]
#切分标准:friedman_mse:费尔德曼均方误差,squared_error,均方误差
criterion=['friedman_mse','squared_error']
#树的最大深度
max_depth = [2,3,5,10,15]
#切分所需的最小样本数
min_samples_split=[2, 4, 6, 10]
#叶节点所需的最小样本数
min_samples_leaf=[1,2,4,6,8]
# 进行拆分时要考虑的最大特征数
max_features = ['sqrt', 'log2', None]
# 定义要进行搜索的超参数网格
hyperparameter = {'n_estimators': n_estimators,
'loss':loss,
'criterion':criterion,
'max_depth': max_depth,
'min_samples_leaf': min_samples_leaf,
'min_samples_split': min_samples_split,
'max_features': max_features}
在下面的代码中,我们创建了随机搜索对象,传递以下参数:
estimator: 估计器,也就是模型param_distributions: 我们定义的参数cv:用于交叉验证的folds 数量n_iter: 不同的参数组合的数量scoring: 评估指标n_jobs: 同时工作的cpu个数(-1代表全部)verbose: 日志冗长度,int:冗长度,0:不输出训练过程,1:偶尔输出,>1:对每个子模型都输出return_train_score: 每一个cross-validation fold 返回的分数random_state: 修复使用的随机数生成器,因此每次运行都会得到相同的结果
随机搜索对象的训练方式与任何其他scikit-learn模型相同。训练之后,我们可以比较所有不同的超参数组合,找到效果最好的组合
#创建用于调整超超参数的模型:梯度提升回归
model=GradientBoostingRegressor(random_state=123)
#使用分层5折交叉验证设置随机搜索
random_cv=RandomizedSearchCV(
estimator=model,
param_distributions=hyperparameter,
cv=4,
n_iter=20,
scoring='r2',
n_jobs=-1,
verbose=1,
return_train_score=True,
random_state=123
)
# 拟合随机搜索
random_cv.fit(X_train,Y_train)
- 使用分层交叉验证随机搜索获得的最佳模型参数
random_cv.best_estimator_
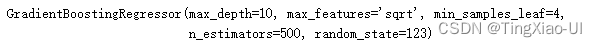
5.4.1.2 使用网络搜索精确超参数范围
在下面的代码中,我们创建了网格搜索对象,传递以下参数:
estimator: 估计器,也就是模型param_grid: 我们定义的参数cv:用于交叉验证的folds 数量scoring: 评估指标n_jobs: 同时工作的cpu个数(-1代表全部)verbose: 日志冗长度,int:冗长度,0:不输出训练过程,1:偶尔输出,>1:对每个子模型都输出random_state: 修复使用的随机数生成器,因此每次运行都会得到相同的结果
#创建一系列要评估的树
trees_grid = {'n_estimators': list(range(400,600,10))}
# 使用随机搜索得到的最佳参数创建模型:
model=GradientBoostingRegressor(
max_depth=10,
max_features='sqrt',
min_samples_leaf=4,
random_state=123
)
# 使用树的范围和梯度提升回归模型的网格搜索对象
grid_search=GridSearchCV(
estimator=model,
param_grid=trees_grid,
cv=5,
scoring='r2',
n_jobs=-1,
verbose=-1
)
#拟合网格搜索
grid_search.fit(X_train,Y_train)
grid_search.best_estimator_

5.5 绘制学习曲线和验证曲线
- 学习曲线学习曲线:模型性能 = f(训练集大小),通过学习曲线观察学习的效果。
验证曲线是横轴为训练集大小,由此来看不同训练集大小设置下的模型准确率。学习曲线可以帮助我们理解训练数据集的大小对机器学习模型的影响。当遇到计算能力限制时,这一点非常有用。下面改变训练数据集的大小,把学习曲线画出来
- 验证曲线: 模型性能(得分) = f(超参数)
验证曲线是横轴为某个超参数的一系列值,由此来看不同参数设置下模型准确率。从验证曲线上可以看到随着超参数设置的改变,模型可能从欠拟合到合适再到过拟合的过程,进而选择一个合适的位置,来提高模型的性能。
在进行模型调参时:其他参数不变,绘制一个参数变化的训练曲线和验证曲线,选择训练效果和验证效果最佳时的参数。依次对每个参数进行绘制图形,调整得到相对优化的模型。
# 使用随机搜索+网络搜索得到的最佳参数创建模型:
model=grid_search.best_estimator_
#生成学习曲线
size_grid = np.array([0.2,0.4,0.6,0.8,1])
_,train_scores,validation_scores = learning_curve(model,X_train,Y_train,
train_sizes = size_grid,
scoring='neg_mean_absolute_error',
cv =5)
#学习曲线可视化
plt.figure()
l=features.shape[0]
plt.plot(size_grid*l,-np.average(train_scores, axis = 1),label="Training score", color = 'red')
plt.plot(size_grid*l, -np.average(validation_scores ,axis = 1),label="validation score",color = 'black')
plt.title('学习曲线')
plt.xlabel('训练集样本大小')
plt.ylabel('MAE')
plt.legend()
plt.show()
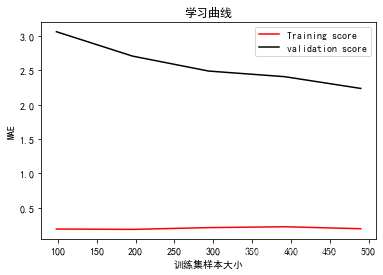
#生成验证曲线
# 创建一系列要评估的树
params_grid= list(range(400,500,10))
#使用
train_scores,validation_scores = validation_curve(model,X_train,Y_train,
param_name='n_estimators',param_range=params_grid,
scoring='neg_mean_absolute_error',cv=5)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
validation_scores_mean = np.mean(validation_scores, axis=1)
validation_scores_std = np.std(validation_scores, axis=1)
#可视化生成训练、验证曲线
plt.figure()
# plt.plot(params_grid, train_scores_mean,color = 'red')
# plt.plot(params_grid,test_scores_mean,color = 'black')
plt.plot(params_grid, -train_scores_mean, label='Training score',color='r')
plt.plot(params_grid, -validation_scores_mean, label='validation score',color='k')
plt.title('验证曲线')
plt.xlabel('number of estimator')
plt.ylabel('MAE')
plt.legend()
plt.show()
#同样的方法可以验证其他变量对训练的影响,多次操作,进行参数调整

6 在测试集上评估最佳模型
我们将使用超参数调整中的最佳模型来对测试集进行预测。 请记住,我们的模型之前从未见过测试集,所以这个性能应该是模型在现实世界中部署时的表现的一个很好的指标。
为了比较,我们还可以查看默认模型的性能。 下面的代码创建最终模型,训练它(会有计时),并评估测试集。
# 默认模型
default_model=GradientBoostingRegressor(random_state=123)
# 选择最佳模型参数
final_model = grid_search.best_estimator_
final_model
%%timeit -n 1 -r 5
default_model.fit(X_train, Y_train)

%%timeit -n 1 -r 5
final_model.fit(X_train, Y_train)
default_model.fit(X_train, Y_train)
final_model.fit(X_train, Y_train)
y_pre_default=default_model.predict(X_test)
test_score_default=metrics.r2_score(Y_test,y_pre_default)
y_pre_final=final_model.predict(X_test)
test_score_final=metrics.r2_score(Y_test,y_pre_final)
round((test_score_final-test_score_default)/test_score_default*100,2)
最终的模型比基线模型的性能提高了大约34%,但代价是显着增加了运行时间。 机器学习通常是一个需要权衡的领域:
- 偏差与方差
- 准确性与可解释性
- 准确性与运行时间
- 以及使用哪种模型
最终决定取决于具体情况。 这里,运行时间的增加不是障碍,因为虽然相对差异很大,但训练时间的绝对量值并不显着。 在不同的情况下,权衡可能不一样,因此我们需要考虑我们正在优化的内容以及我们必须使用的限制。
6.1 误差分析
为了了解预测,我们可以绘制下面两个值的分布:
- 测试集上的真值
- 测试集上的预测值
残差的分布情况
6.2 残差分析回归模型的拟合效果
在回归分析中,通常用残差分析来判断回归模型的拟合效果以评估回归模型好坏,优秀/合格。
残差分析的两种方法:
- 残差图:plt(errir=y_pre-y_true),若残差点比较均匀的落在水平区域中,说明模型比较合适;若区域是倾斜的,说明残差与横坐标有线性关系,回归模型效果不好;带状区域的宽度越窄,说明模型的拟合精度越高。残差图分布越均匀、宽度越窄,则模型拟合效果越好
- 偏残差图(成分残差图): 描述的是自变量和残差之间的关系,偏残差实际上是将每个样本对应的残差分解给各个自变量。
- 决定系数(R平方):一般R平方越大,残差平方和就越小,从而回归模型的拟合效果就越好
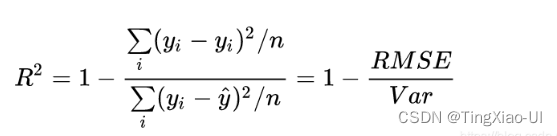
R2通俗地理解为使用均值作为误差基准,看预测误差是否大于或者小于均值基准误差。
* R2_score = 1,样本中预测值和真实值完全相等,没有任何误差,表示回归分析中自变量对因变量的解释越好。
* R2_score = 0,此时分子等于分母,样本的每项预测值都等于均值。
* R2_score < 0,此时分子大于分母,预测的结果还不如测试集中的平均值。
6.2.1残差图
通过绘制残差图能够直观的发现真实值与预测值之间的差异或垂直距离,通过真实值与预测值之间的差异来对回归模型进行评估。残差图可以作为图形分析方法,可以对回归模型进行评估、获取模型的异常值,同时还可以检查模型是否是线性的,以及误差是否随机分布。
线性和非线性
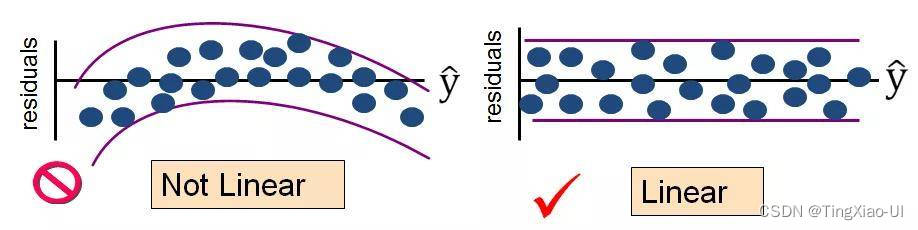
等方差和异方差
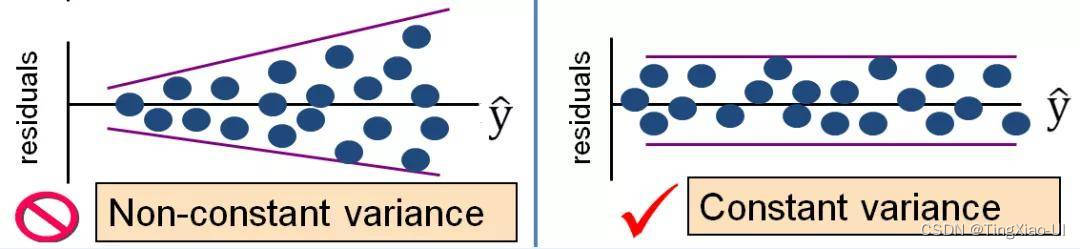
线性独立和不独立
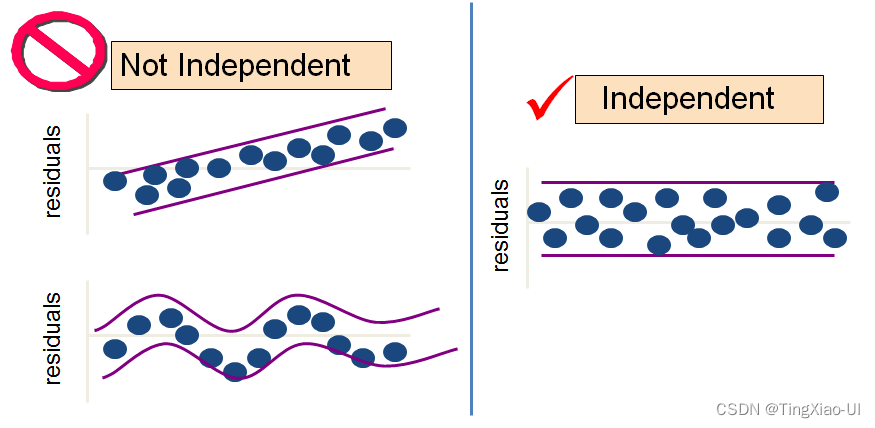
理想情况下,回归残差将有一个完美的正态分布。
final_model.fit(X_train, Y_train)
y_pre_final=final_model.predict(X_test)
# 计算残差
residuals = y_pre_final - Y_test
# 最终预测的密度图和测试值
fig = plt.figure(figsize=(15,5))
ax1 = fig.add_subplot(131)
sea.kdeplot(y_pre_final, label = 'Predictions',ax=ax1)
sea.kdeplot(Y_test, label = 'Real_values',ax=ax1)
plt.legend()
ax1.set_xlabel('Price')
ax1.set_ylabel('Density')
ax1.set_title('Test Values and Predictions')
# 绘制残差分布散点图
ax2 = fig.add_subplot(132)
data_desc=pd.DataFrame(residuals).describe()
index=pd.DataFrame(residuals).index
q1=data_desc[0]['25%']
q3=data_desc[0]['75%']
iqr=q3-q1
l=len(residuals)
ax2.plot(index,[q1-1.5*iqr]*l,'r')
ax2.plot(index,[q3+3*iqr]*l,'y')
ax2.plot(index,[q3+1.5*iqr]*l,'r')
ax2.plot(index,[q1-3*iqr]*l,'y')
ax2.scatter(Y_test,residuals)
ax2.set_xlabel('price')
ax2.set_ylabel('Error')
ax2.set_title('Scatter')
# sea.regplot(x=range(len(residuals)), y=residuals, data=residuals)
# 绘制残差分布直方图
ax3 = fig.add_subplot(133)
# plt.hist(residuals, color = 'red', bins = 200,edgecolor = 'black')
sea.histplot(data=pd.DataFrame(residuals),kde=True,bins=20)
ax3.set_xlabel('Error')
ax3.set_ylabel('Count')
ax3.set_title('残差的直方图显示所有观测值的残差分布')
plt.tight_layout() # 防止文字遮挡
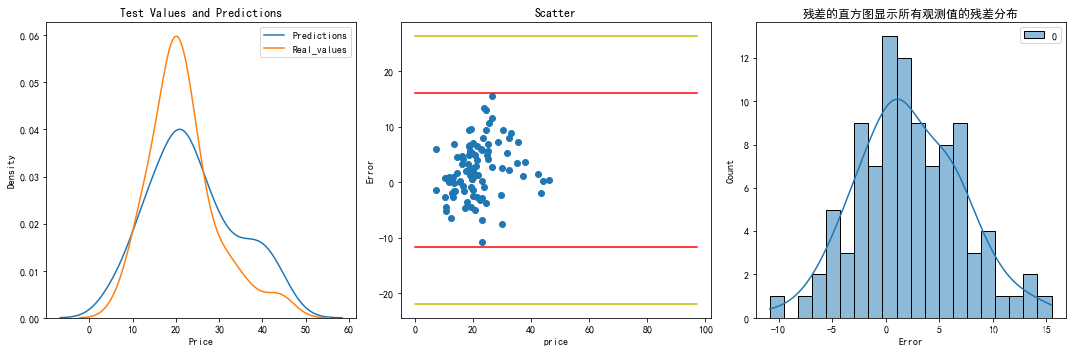
分布看起来几乎相同。模型在预测价格在40附近时不太准确,同时预测值 更接近中位数。
另一个诊断图是残差的直方图。 理想情况下,我们希望残差是正态分布的,这意味着模型在两个方向(高和低)上误差是相同的。残差接近正态分布。
理想情况下,回归残差将有一个完美的正态分布。普通最小二乘法在数学上保证产生均值为零的残差,因此,中位数(50%)的符号表示偏斜的方向,而中位数的大小表示偏斜的程度。本例中中位数为0.67,表示向左偏斜(看拖尾方向来判断偏斜方向)。
如果残差有一个很好的钟形分布,第一四分位和第三四分位应该有大约相同的幅度。
最小残差和最大残差提供了一种快速的方法来检测数据中的极端离群值,因为极端离群值(在响应变量中)产生较大的残差。
6.2.2 偏残差图
data_plot=pd.DataFrame(X_test,columns=data_select.drop('price',axis=1).columns)
residuals=pd.DataFrame(residuals.reshape((-1,1)),columns=['残差'])
data_plot=pd.concat([data_plot,residuals],axis=1)
# data_plot
drop_lists=[col for col in data_plot.columns if 'cut' in col ]
data_plot=data_plot.drop(drop_lists,axis=1)
data_plot
plt.figure(figsize=(15,15))
for i,col in enumerate(data_plot.drop('残差',axis=1).columns):
ax=plt.subplot(5,3,i+1)
ax.set_xlabel(col)
sea.regplot(data=data_plot,x=col,y='残差')
# sea.lmplot(data=data_plot,x=col,y='残差')
plt.tight_layout()
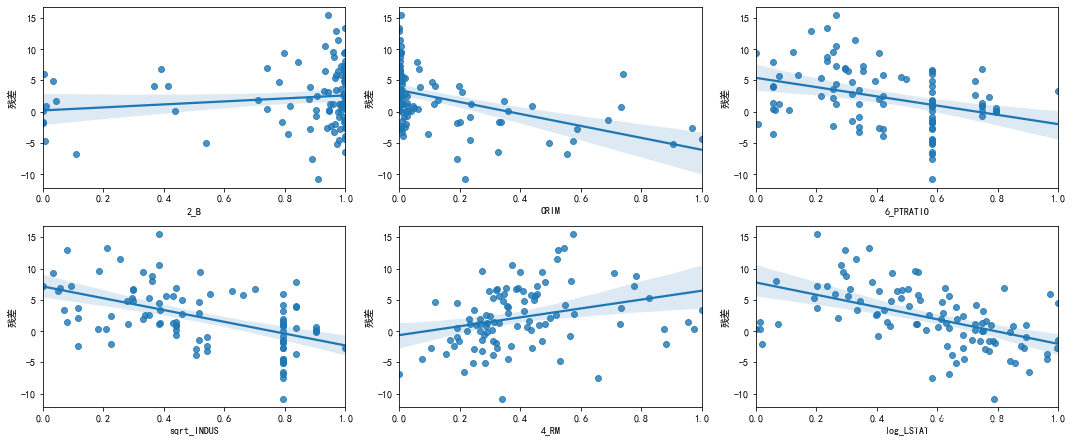
((y_pre_final-Y_test)/Y_test).mean()*100

final_model.fit(X_train, Y_train)
Y_pre=final_model.predict(X_train)
round(metrics.r2_score(Y_train, Y_pre)*100,2)
Y_pre=final_model.predict(X_test)
round(metrics.r2_score(Y_test, Y_pre)*100,2)
6.3 小结
在4,5,6 步我们做了一下几件事:
- 特征缩放
- 评估和比较几种机器学习方法
- 超参数使用随机搜索和交叉验证来调整机器学习模型
- 评估测试集上的最佳模型
结果表明:
- 机器学习适用于我们的问题,最终模型能够将房屋租赁价格的预测误差控制在9%以内。
- 模型过拟合,虽然模型在训练集R2达到100%,但在测试集不到60%,在正式出报告前后续可继续调参。
- 我们还看到,超参数调整能够改善模型的性能,尽管在投入的时间方面成本相当高。这是一个很好的提示,正确的特征工程和收集更多数据(如果可能!)比微调模型有更大的回报。
- 我们还观察了运行时间与精度之间的权衡,这是我们在设计机器学习模型时必须考虑的众多因素之一。
我们知道我们的模型是准确的,但我们知道为什么它能做出预测?机器学习过程的下一步至关重要:尝试理解模型如何进行预测。实现高精度是很好的,但如果我们能够找出模型能够准确预测的原因,那么我们也可以使用这些信息来更好地理解问题。例如,
- 模型依靠哪些特征来推断预测生还与否?
- 可以使用此模型进行特征选择,并实现更易于解释的更简单模型吗?
下面,我们将尝试回答这些问题并从项目中得出最终结论!
7. 解释模型结果
机器学习经常被批评为一个黑盒子 criticized as being a black-box:我们把数据在这边放进去,它在另一边给了我们答案。 虽然这些答案通常都非常准确,但该模型并未告诉我们它实际上如何做出预测。 这在某种程度上是正确的,但我们可以通过多种方式尝试并发现模型如何“思考”,例如 Locally Interpretable Model-agnostic Explainer (LIME). 这种方法试图通过学习围绕预测的线性回归来解释模型预测,这是一个易于解释的模型!
我们将探索几种解释模型的方法:
- 特征重要性
- 本地可解释的模型不可知解释器 (LIME)
- 检查整体中的单个决策树
# 机器学习模型
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn import tree
# LIME用于解释预测
import lime
import lime.lime_tabular
7.1 特征重要性
我们可以解释决策树集合的基本方法之一是通过所谓的特征重要性。 这些可以解释为最能预测目标的变量。 虽然特征重要性的实际细节非常复杂. (here is a Stack Overflow question on the subject,但是我们可以使用相对值来比较特征并确定哪些与我们的问题最相关。
在scikit-learn中,从训练好的树中提取特征重要性非常容易。 我们将特征重要性存储在数据框中以分析和可视化它们。
# 将特征重要性提取到数据结构中
feature_results = pd.DataFrame({'feature': list(train_features.columns),
'importance': final_model.feature_importances_})
# 显示最重要的前十名
feature_results = feature_results.sort_values('importance', ascending = False).reset_index(drop=True)
feature_results.head(10)
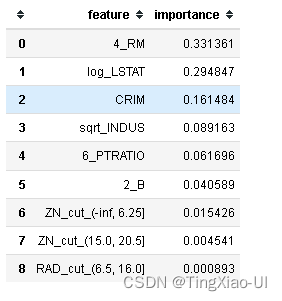
4_RM、log_LSTAT、CRIM是最重要的特征,这之后,特征的相对重要性大幅下降,这表明我们可能不需要保留所有特征来创建具有几乎相同性能的模型。
plt.style.use('fivethirtyeight')
feature_results.loc[:10, :].plot(x = 'feature', y = 'importance',
edgecolor = 'k',
kind='barh', color = 'blue');
plt.xlabel('Relative Importance', size = 20); plt.ylabel('')
plt.title('Feature Importances from Random Forest', size = 30);
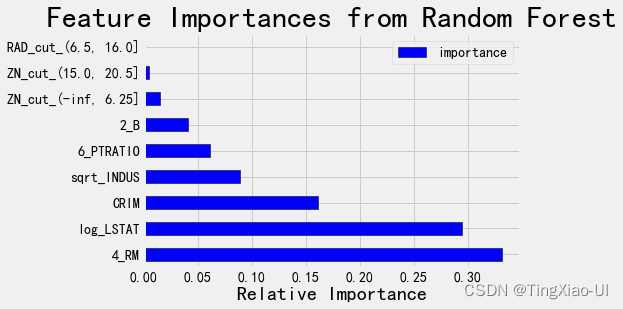
7.1.1 使用特征重要性进行特征选择
# 提取最重要特征的名称
most_important_features = feature_results['feature'][:6]
# 找到与每个特征名称对应的索引
indices = [list(train_features.columns).index(x) for x in most_important_features]
# 数据集中只保留最重要的特征
X_reduced = X_train[:,indices]
X_test_reduced = X_test[:,indices]
print('Most important training features shape: ', X_reduced.shape)
print('Most important testing features shape: ', X_test_reduced.shape)
让我们看看在梯度提升回归中使用减少的特征集。 性能如何受到影响?
#梯度提升分类树
#在全部特征上拟合并测试
#分层交叉验证评估
GB_score_all=round(-cross_val_score(final_model,X_train,Y_train, scoring='neg_mean_absolute_error', cv=5).mean(),3)
print('全部特征')
print('MAE:',GB_score_all)
# 在5个最重要的特征上拟合并测试(即减少后的特征上)
#分层交叉验证评估
GB_score_reduced=round(-cross_val_score(final_model,X_reduced,Y_train, scoring='neg_mean_absolute_error', cv=5).mean(),3)
print('减少特征')
print('MAE:',GB_score_reduced)

随着特征数量的减少,模型结果变差,我们将保留最终模型的所有特征。 减少特征数量的初衷是因为我们总是希望构建最简约的模型:
- 即具有足够特征的最简单模型
- 使用较少特征的模型将更快地训练并且通常更容易解释。
在现在这种情况下,保留所有特征并不是主要问题,因为训练时间并不重要,我们仍然可以使用许多特征进行解释。
7.2 部分依赖图(PDP)和个体条件期望图(ICE)
部分依赖图 (PDP) 和个体条件期望 (ICE) 图可用于可视化和分析训练目标与一组输入特征之间的交互关系。
- PDP:特征变量与模型预测结果(样本预测结果的平均值)影响的函数关系,反映的是平均水平
- ICE:特征变量与模型预测结果(样本预测结果)影响的函数关系
7.2.1 部分依赖图(PDP)
- 部分依赖图:能够展现出一个或两个特征变量对模型预测结果(样本预测结果的平均值)影响的函数关系、边际效应:近似线性关系、单调关系或者更复杂的关系。
使用PDP方法对梯度提升回归模型结果进行解析
PDP图的优点在于易实施,缺点在于不能反映特征变量本身的分布情况,且拥有苛刻的假设条件——变量之间严格独立。若变量之间存在相关关系,会导致计算过程中产生过多的无效样本,估计出的值比实际偏高。另一个缺点是样本整体的非均匀效应(Heterogeneous effect):PDP只能反映特征变量的平均水平,忽视了数据异质对结果产生的影响。
from sklearn.inspection import PartialDependenceDisplay
final_model.fit(train_features,Y_train)
PartialDependenceDisplay.from_estimator(final_model,train_features,train_features.columns,kind='average')
plt.tight_layout()#防止文字遮挡
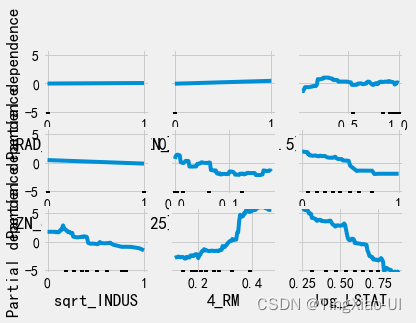
7.2.1.1 根据PDP进行特征特征选择
- 当某个特征的PDP曲线几乎水平或者无规律抖动的时候, 这个特征可能是无用的特征.
- 当某个特征的PDP曲线非常陡峭的时候, 说明这个特征的贡献度是比较大的.
7.2.2个体条件期望图(ICE)
个体条件期望图(ICE Plot)计算方法与PDP类似,它刻画的是每个样本的预测值与单一变量之间的关系。个体条件期望图消除了非均匀效应的影响,它的原理和实现方法如下:对某一个体,保持其他变量不变,随机置换我们选定的特征变量的取值,放入黑箱模型输出预测结果,最后绘制出针对这个个体的单一特征变量与预测值之间的关系图。
ICE图的优点在于易于理解,能够避免数据异质的问题。在ICE图提出之后,人们又提出了衍生ICE图,能够进一步检测变量之间的交互关系并在ICE图中反映出来。
ICE图的缺点在于只能反映单一特征变量与目标之间的关系,仍然受制于变量独立假设的要求,同时ICE图像往往由于个体过多导致图像看起来过于冗杂,不容易获取解释信息。
plt.figure(figsize=(10,8))
features=['sqrt_INDUS','4_RM','log_LSTAT']
PartialDependenceDisplay.from_estimator(final_model, train_features, features,kind='individual')
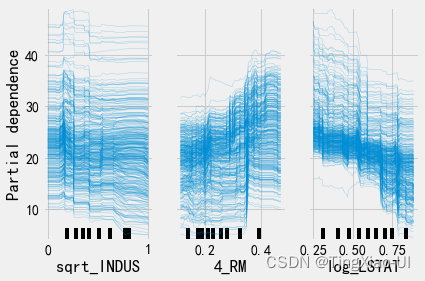
- 部分依赖图(PDP)和个体条件期望图(ICE)一起绘制:kind=‘both’
PartialDependenceDisplay.from_estimator(final_model, train_features, features,kind='both')
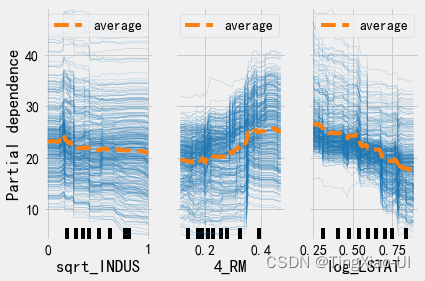
- 上图反映了’sqrt_INDUS’,‘4_RM’,'log_LSTAT’三个特征模型预测结果的影响,随着特征增长,模型预测结果呈上升、下降或保持水平的变化趋势
- 每个样本个体并不一定遵循相同的变化趋势
- 相较于PDP的一概而论,ICE图能够更准确的反映特征变量与目标之间的关系
PartialDependenceDisplay.from_estimator(final_model, train_features, features,kind='both',centered=True)
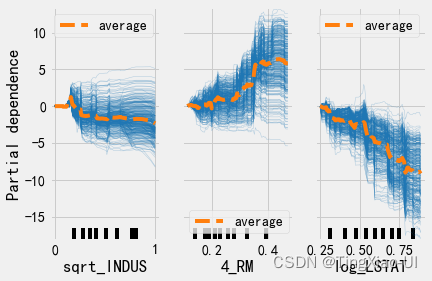
7.3 Locally Interpretable Model-agnostic Explanations - 本地可解释的与模型无关的解释
我们将使用LIME9(LIME to explain individual predictions )来解释模型所做的个别预测。 LIME是一项相对较新的工作,旨在通过用线性模型近似预测周围的区域来展示机器学习模型的思考方式。
我们将试图解释模型在两个例子上得到的预测结果:
- 其中一个例子得到的预测结果非常差
- 另一个例子得到的预测结果非常好。
我们将仅仅使用减少后的4个特征来帮助解释。 虽然在4个最重要的特征上训练的模型稍微不准确,但我们通常必须为了可解释性的准确性进行权衡!
final_model.fit(X_reduced, Y_train)
final_model_reduced_pred = final_model.predict(X_test_reduced)
# 找到残差
residuals = abs(final_model_reduced_pred - Y_test)
# 提取最差和最好的预测的数据集
wrong = X_test_reduced[np.argmax(residuals), :]
right = X_test_reduced[np.argmin(residuals), :]
# 创造一个解释器对象
explainer = lime.lime_tabular.LimeTabularExplainer(
training_data=X_reduced,
feature_names=list(most_important_features),
class_names=['bad', 'good'],
mode='regression'
)
对最差预测的解释:
# 显示最差实例的预测值和真实值
print('Prediction: %0.4f' % final_model.predict(wrong.reshape(1, -1)))
print('Actual Value: %0.4f' % Y_test[np.argmax(residuals)])
# 最差预测的解释
wrong_exp = explainer.explain_instance(data_row = wrong, predict_fn =final_model.predict)
# wrong_exp.show_in_notebook(show_table=True)
# # 画出预测解释
wrong_exp.as_pyplot_figure()
plt.title('Explanation of Prediction', size = 28)
plt.xlabel('Effect on Prediction', size = 22)
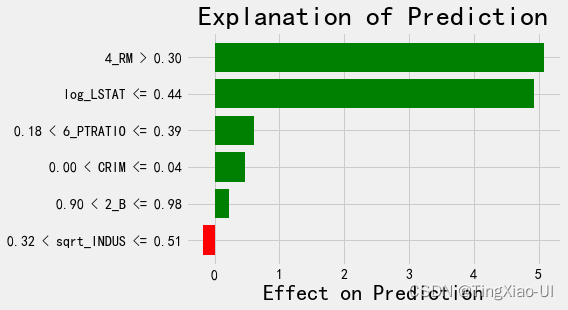
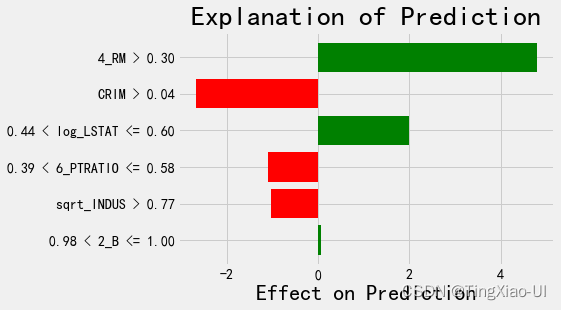
对最好预测的解释:
# 显示最好实例的预测值和真实值
print('Prediction: %0.4f' % final_model.predict(right.reshape(1, -1)))
print('Actual Value: %0.4f' % Y_test[np.argmin(residuals)])
# 最好预测的解释
right_exp = explainer.explain_instance(data_row = right, predict_fn =final_model.predict)
# 画出预测解释
right_exp.as_pyplot_figure()
plt.title('Explanation of Prediction', size = 28)
plt.xlabel('Effect on Prediction', size = 22)
8 得出结论&&记录发现
8.1 得出结论
机器学习管道的最后部分可能是最重要的:我们需要将我们学到的所有内容压缩成一个简短的摘要,仅突出最重要的发现。
就此项目而言,我们很简洁地总结了我们的工作。 但是,在我们呈现和相应地定制信息时,了解我们的受众非常重要。 这是一个用来申请工作的“作业”,考虑到这一点,这是我们需要在30秒内介绍的项目内容:
- 使用波士顿房屋租赁价格数据,可以建立一个模型,可以价格,误差在8%以内。
log_LSTAT、4_RM、sqrt_INDUS、sqrt_TAX和5_PTRATIO是预测价格的最相关特征。
如果有人要求提供详细信息,那么我们可以轻松地解释所有实施步骤,并展示我们(希望)有充分记录的工作。 机器学习项目的另一个重要方面是:
- 你已经注解了所有代码并使其易于跟进!
- 你希望别人(或者你自己在几个月内)能够看到你的工作并完全理解你做出的决定。
理想情况下,你应该编写代码,以便再次使用它。 即使我们自己做项目,也可以练习正确的文档,当你想重新审视项目时,它会让你的生活更轻松。
8.2 记录发现
技术项目经常被忽视的部分是文档和报告。 我们可以在世界上做最好的分析,但如果我们没有清楚地传达我们发现的结果,那么它们就不会产生任何影响!当我们记录数据科学项目时,我们会采用所有版本的数据和代码并对其进行打包,以便我们的项目可以被其他数据科学家复制或构建。 重要的是要记住:
- 阅读代码的频率高于编写代码
- 如果我们几个月后再回来的话,我们希望确保我们的工作对于其他人和我们自己都是可以理解的,这意味着在代码中添加有用的注释并解释我们的推理。
Jupyter notebook 是一个很好的文档工具,因为它们允许一个接一个地解释和编码。Jupyter notebook 也可以成为将结果传达给他人的良好平台。 使用笔记本扩展,我们可以隐藏最终报告中的代码,因为虽然很难相信,但并不是每个人都希望在文档中看到一堆Python代码!此外还可以直接下载为pdf或html,然后与他人共享。
完成Jupyter notebook后,原作者将其下载为.tex,在texStudio中进行了一些小改动,然后将其编译为pdf。最终版本看起来比默认的Jupyter Notebook pdf好一点,并且学习一些latex以创建更专业的报告是很有意义的!
