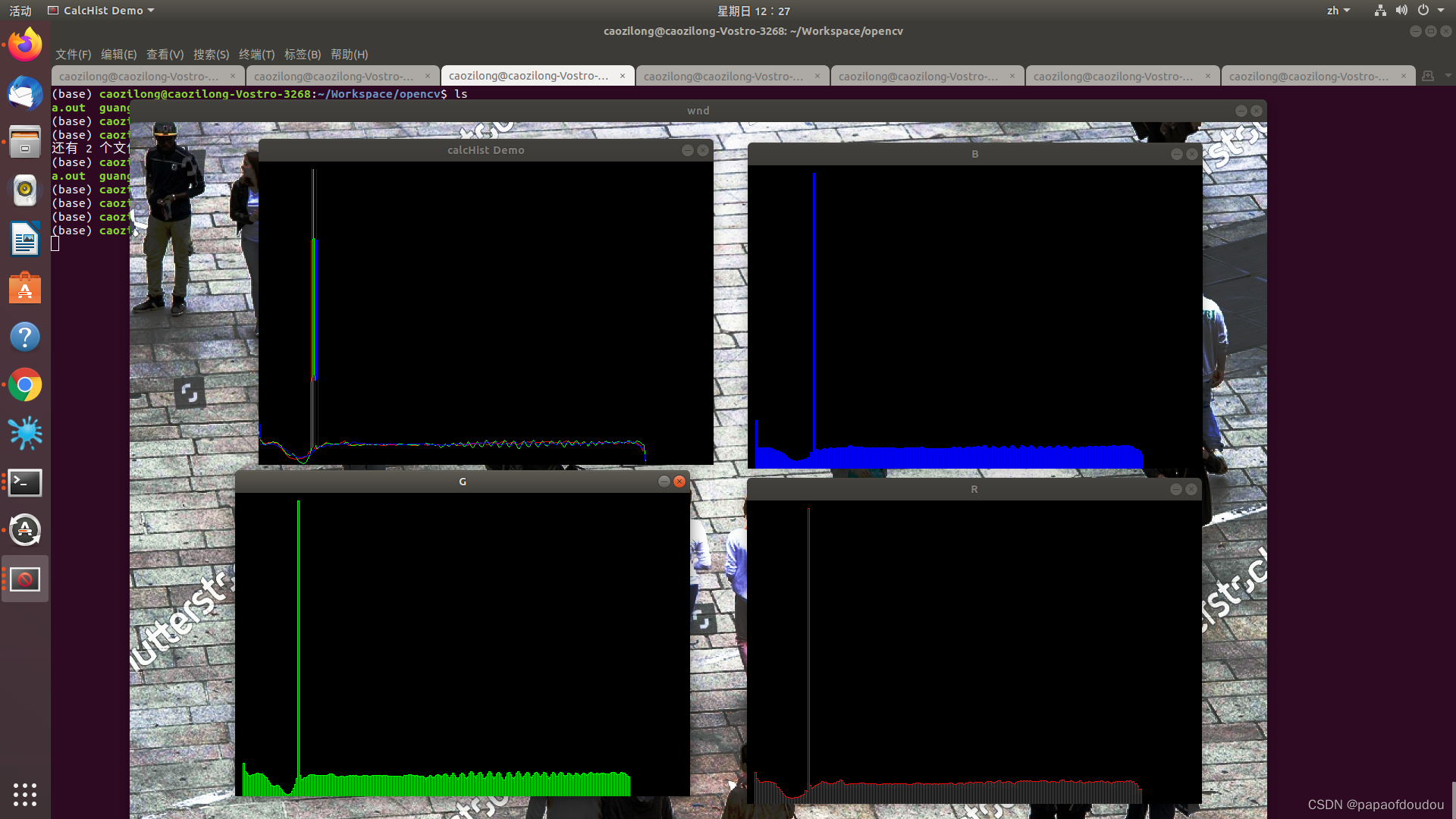
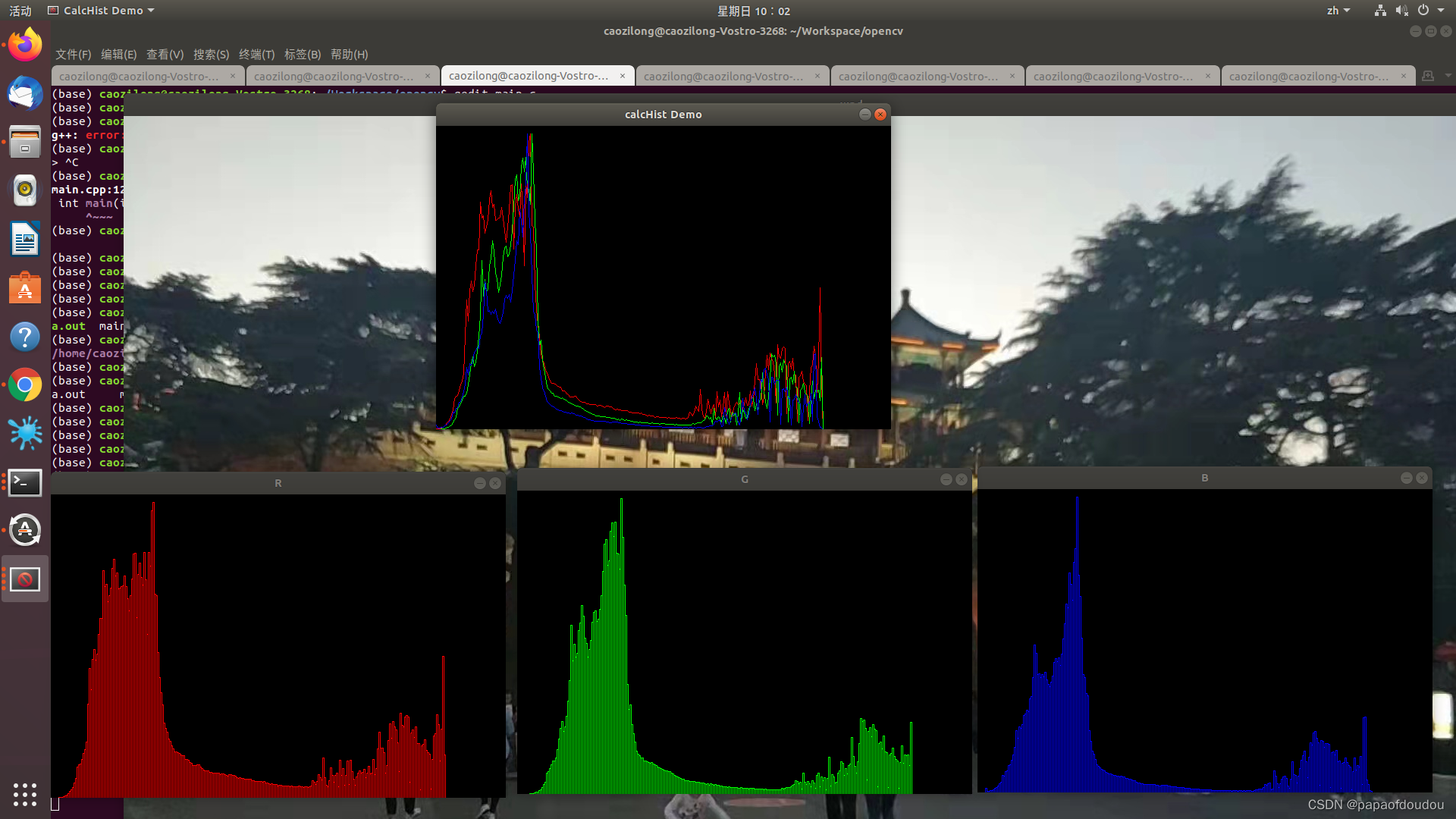
直方图是我们在照片中使用来查看图像中每个值有多少像素,照片中的每个像素的值都从0(黑色)到255(白色),图的左侧代表音阶的暗色调,右侧代表较亮的色调。在彩色摄影中,每个像素对于每种颜色都有其自己的值(0-255)。图片中的直方图显示了每种颜色(红色,蓝色和绿色)的像素值分布.
图像直方图,也叫灰度直方图,反映了图像像素分布的统计特征,是图像处理中简单有效的工具,图像直方图广泛地应用于图像处理的各个领域,如:特征提取,图像匹配,灰度图像的阈值分割,基于颜色的图像检索以及图像分类。
图像的直方图的形态很大程度上可直观的反映图像的质量情况,比如根据下图所示,会很快发现一张图片是否过量还是过暗。

图像直方图的优点是,计算量较小,且具有图像平移,旋转,缩放不变性等。
数学原理
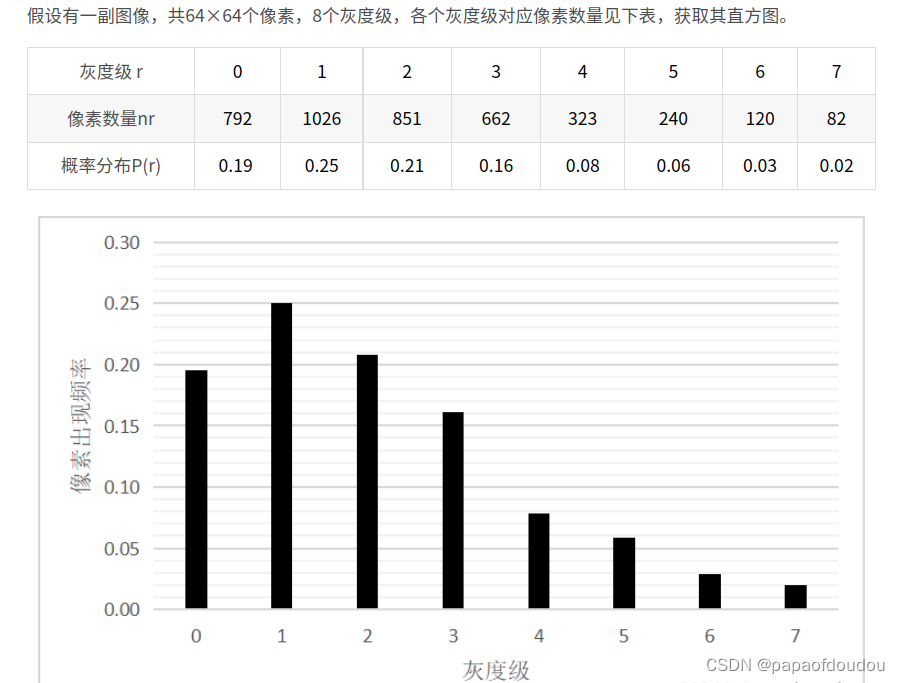
图像灰度直方图计算:
其中,W,H分别表示图像的宽和高,表示图像中像素值为r的数量,
表示图像中像素值为r的比率,L是指图像灰度级数,比如,8BIT的灰度图像L=2^8=256.其存在256个色阶,即0-255。

OPENCV获取直方图:
//获得直方图
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main(int argc, char** argv)
{
//----------------------example 1-------------------------------//
Mat src, dst;
/// Load image
src = imread("/home/caozilong/165823915.jpg");
if (!src.data)
{
cout << "load image failed" << endl;
return -1;
}
/// Separate the image in 3 places ( R, G and B )
vector<Mat> rgb_planes;
Mat hsv;
cvtColor(src, hsv, COLOR_BGR2HSV);
split(hsv, rgb_planes);
split(src, rgb_planes);
/// Establish the number of bins
int histSize = 256;
/// Set the ranges ( for R,G,B) )
float range[] = { 0, 255 };
const float* histRange = { range };
bool uniform = true; bool accumulate = false;
Mat r_hist, g_hist, b_hist;
/// Compute the histograms:
calcHist(&rgb_planes[2], 1, 0, Mat(), r_hist, 1, &histSize, &histRange, uniform, accumulate);
calcHist(&rgb_planes[1], 1, 0, Mat(), g_hist, 1, &histSize, &histRange, uniform, accumulate);
calcHist(&rgb_planes[0], 1, 0, Mat(), b_hist, 1, &histSize, &histRange, uniform, accumulate);
// Draw the histograms for R, G and B
int hist_w = 600; int hist_h = 400;
int bin_w = cvRound((double)hist_w / histSize);
Mat rgb_hist[3];
for (int i = 0; i < 3; ++i)
{
rgb_hist[i] = Mat(hist_h, hist_w, CV_8UC3, Scalar::all(0));
}
Mat histImage(hist_h, hist_w, CV_8UC3, Scalar(0, 0, 0));
/// Normalize the result to [ 0, histImage.rows-10]
normalize(r_hist, r_hist, 0, histImage.rows - 10, NORM_MINMAX);
normalize(g_hist, g_hist, 0, histImage.rows - 10, NORM_MINMAX);
normalize(b_hist, b_hist, 0, histImage.rows - 10, NORM_MINMAX);
/// Draw for each channel
for (int i = 1; i < histSize; i++)
{
line(histImage, Point(bin_w * (i - 1), hist_h - cvRound(r_hist.at<float>(i - 1))),
Point(bin_w * (i), hist_h - cvRound(r_hist.at<float>(i))),
Scalar(0, 0, 255), 1);
line(histImage, Point(bin_w * (i - 1), hist_h - cvRound(g_hist.at<float>(i - 1))),
Point(bin_w * (i), hist_h - cvRound(g_hist.at<float>(i))),
Scalar(0, 255, 0), 1);
line(histImage, Point(bin_w * (i - 1), hist_h - cvRound(b_hist.at<float>(i - 1))),
Point(bin_w * (i), hist_h - cvRound(b_hist.at<float>(i))),
Scalar(255, 0, 0), 1);
}
for (int j = 0; j < histSize; ++j)
{
int val = saturate_cast<int>(r_hist.at<float>(j));
rectangle(rgb_hist[0], Point(j * 2 + 10, rgb_hist[0].rows), Point((j + 1) * 2 + 10, rgb_hist[0].rows - val), Scalar(0, 0, 255), 1, 8);
val = saturate_cast<int>(g_hist.at<float>(j));
rectangle(rgb_hist[1], Point(j * 2 + 10, rgb_hist[1].rows), Point((j + 1) * 2 + 10, rgb_hist[1].rows - val), Scalar(0, 255, 0), 1, 8);
val = saturate_cast<int>(b_hist.at<float>(j));
rectangle(rgb_hist[2], Point(j * 2 + 10, rgb_hist[2].rows), Point((j + 1) * 2 + 10, rgb_hist[2].rows - val), Scalar(255, 0, 0), 1, 8);
}
/// Display
namedWindow("calcHist Demo", CV_WINDOW_AUTOSIZE);
namedWindow("wnd");
imshow("calcHist Demo", histImage);
imshow("wnd", src);
imshow("R", rgb_hist[0]);
imshow("G", rgb_hist[1]);
imshow("B", rgb_hist[2]);
waitKey();
}g++ new.cpp `pkg-config --cflags --libs opencv`直方图均值化
直方图均衡化是通过拉伸像素强度的分布范围,使得在0~255灰阶上的分布更加均衡,提高了图像的对比度,达到改善图像主观视觉效果的目的。对比度较低的图像适合使用直方图均衡化方法来增强图像细节。
//彩色图像直方图均衡化
#include<opencv2/opencv.hpp>
#include<iostream>
#include<cmath>
using namespace cv;
using namespace std;
const char* output = "histogram iamge";
int main(int argc, char** argv)
{
Mat src, dst, dst1;
src = imread("/home/caozilong/165823915.jpg");
if (!src.data)
{
printf("could not load image...\n");
return -1;
}
char input[] = "input image";
namedWindow(input, 0);
namedWindow(output, 0);
resizeWindow(input, 600, 400);
imshow(input, src);
//分割通道
vector<Mat>channels;
split(src, channels);
Mat blue, green, red;
blue = channels.at(0);
green = channels.at(1);
red = channels.at(2);
//分别对BGR通道做直方图均衡化
equalizeHist(blue, blue);
equalizeHist(green, green);
equalizeHist(red, red);
//合并通道
merge(channels, dst);
resizeWindow(output, 600, 400);
imshow(output, dst);
waitKey(0);
return 0;
}g++ main.cpp `pkg-config --cflags --libs opencv`可以看到对比度确实增加了
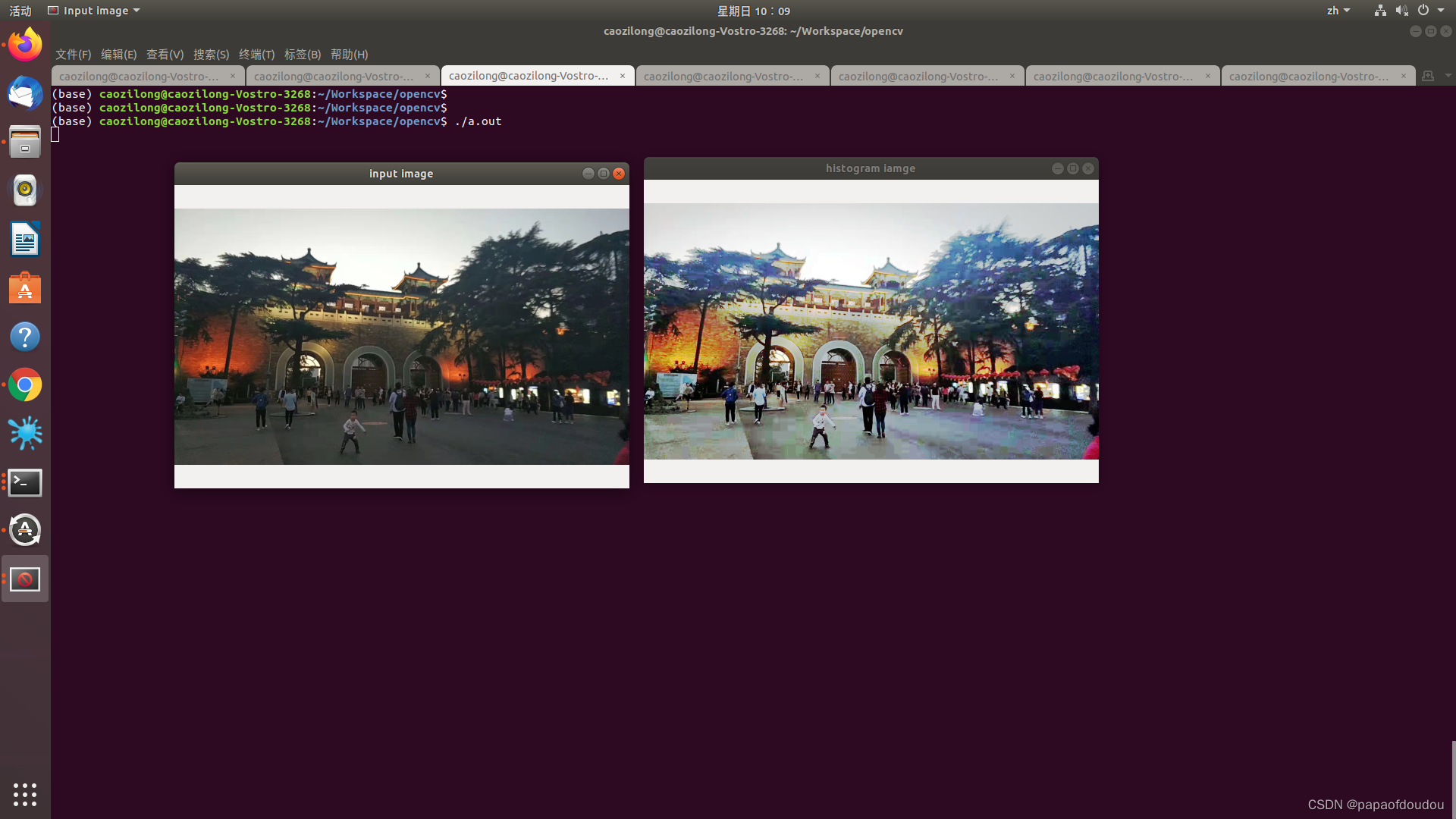
但是对于那些曝光良好,直方图表现均匀的图像,均值化的效果并不明显:
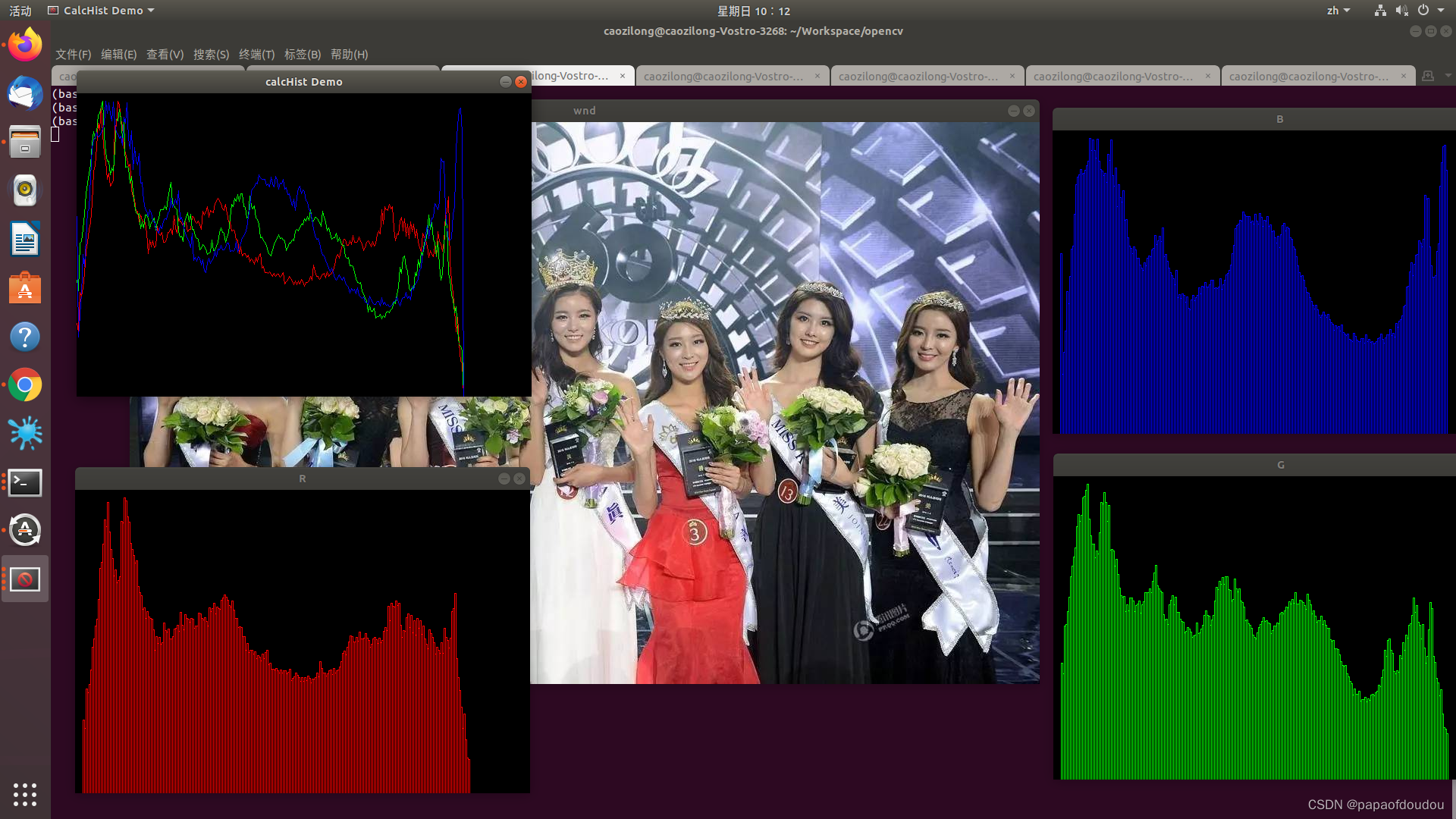
然后,进行均值化后的效果,可以发现,对比度的增加效果并不明显:

另一个例子,原始图片:
 图像直方图:
图像直方图:
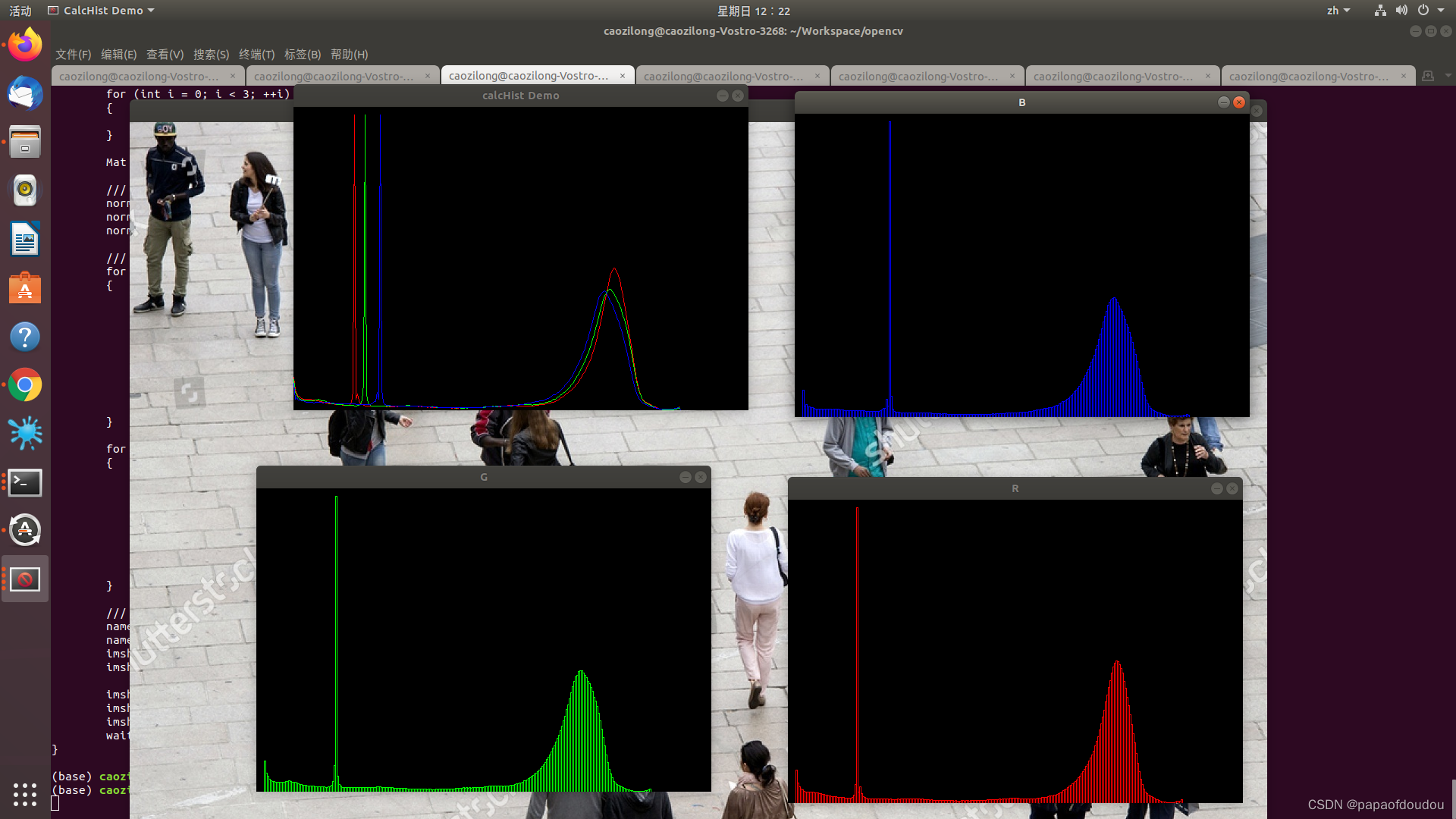
进行直方图均值化后的图像:

对应的直方图为: