损失函数(Loss Function):
损失函数(loss function)就是用来度量模型的预测值f(x)与真实值Y的差异程度的运算函数,它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。
损失函数的作用:
损失函数使用主要是在模型的训练阶段,每个批次的训练数据送入模型后,通过前向传播输出预测值,然后损失函数会计算出预测值和真实值之间的差异值,也就是损失值。得到损失值之后,模型通过反向传播去更新各个参数,来降低真实值与预测值之间的损失,使得模型生成的预测值往真实值方向靠拢,从而达到学习的目的。
几个常用的损失函数:
均方误差损失函数(MSE):
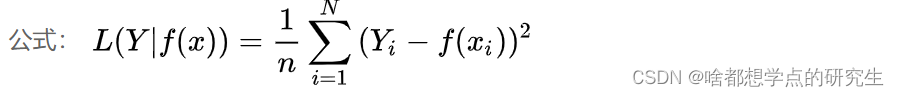
在回归问题中,均方误差损失函数用于度量样本点到回归曲线的距离,通过最小化平方损失使样本点可以更好地拟合回归曲线。均方误差损失函数(MSE)的值越小,表示预测模型描述的样本数据具有越好的精确度。由于无参数、计算成本低和具有明确物理意义等优点,MSE已成为一种优秀的距离度量方法。尽管MSE在图像和语音处理方面表现较弱,但它仍是评价信号质量的标准,在回归问题中,MSE常被作为模型的经验损失或算法的性能指标。
L2 Loss:
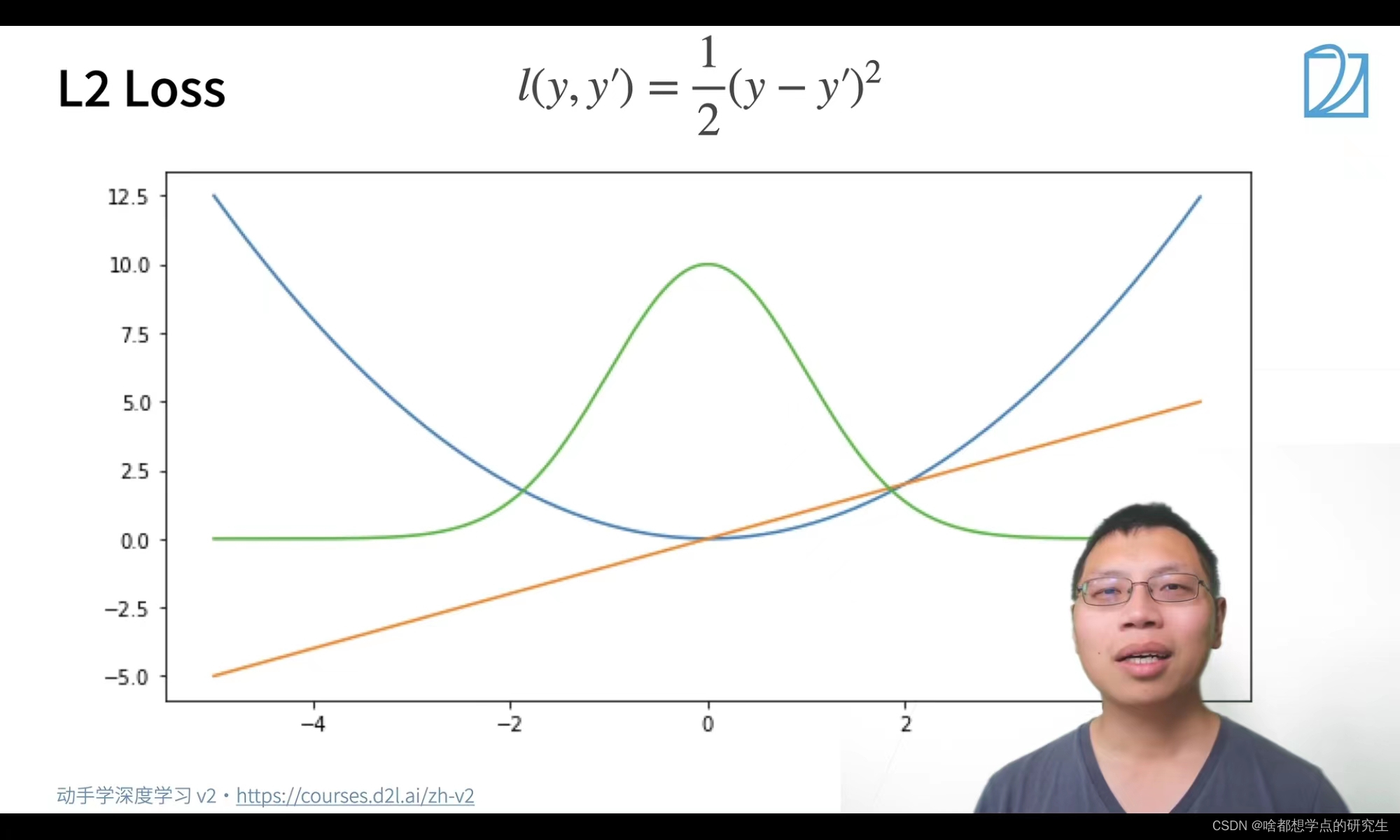
?L2 loss:图中蓝色是L2 Loss损失函数;?绿色为L2 Loss的似然函数;橙色为L2 Loss的梯度函数

?图中可以看出L2 Loss损失函数的特点,当里极值点较远的时候其以较大的梯度绝对值下降当靠近我们的极值点时它的梯度变得很小,当然也有它不足的地方,就是当离极值点很远的时候,它的梯度很大,离原点较远的时候,我们可能不需要那么大的梯度。
L1 loss:
L1损失又称为曼哈顿距离,表示残差的绝对值之和。L1损失函数对离群点有很好的鲁棒性,但它在残差为零处却不可导。另一个缺点是更新的梯度始终相同,也就是说,即使很小的损失值,梯度也很大,这样不利于模型的收敛。针对它的收敛问题,一般的解决办法是在优化算法中使用变化的学习率,在损失接近最小值时降低学习率。
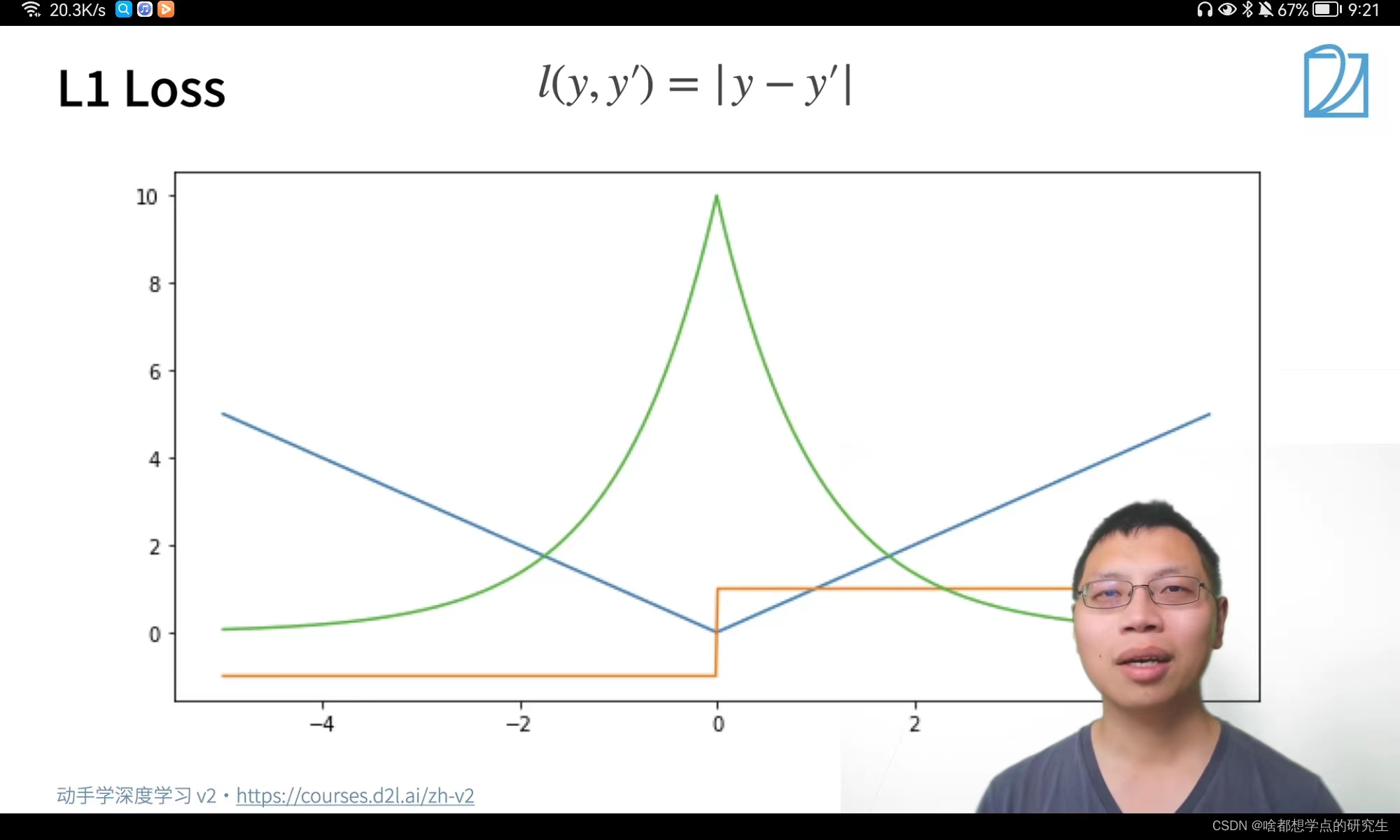
??L1?loss:图中蓝色是L1?Loss损失函数;?绿色为L1?Loss的似然函数;橙色为L1?Loss的梯度函数
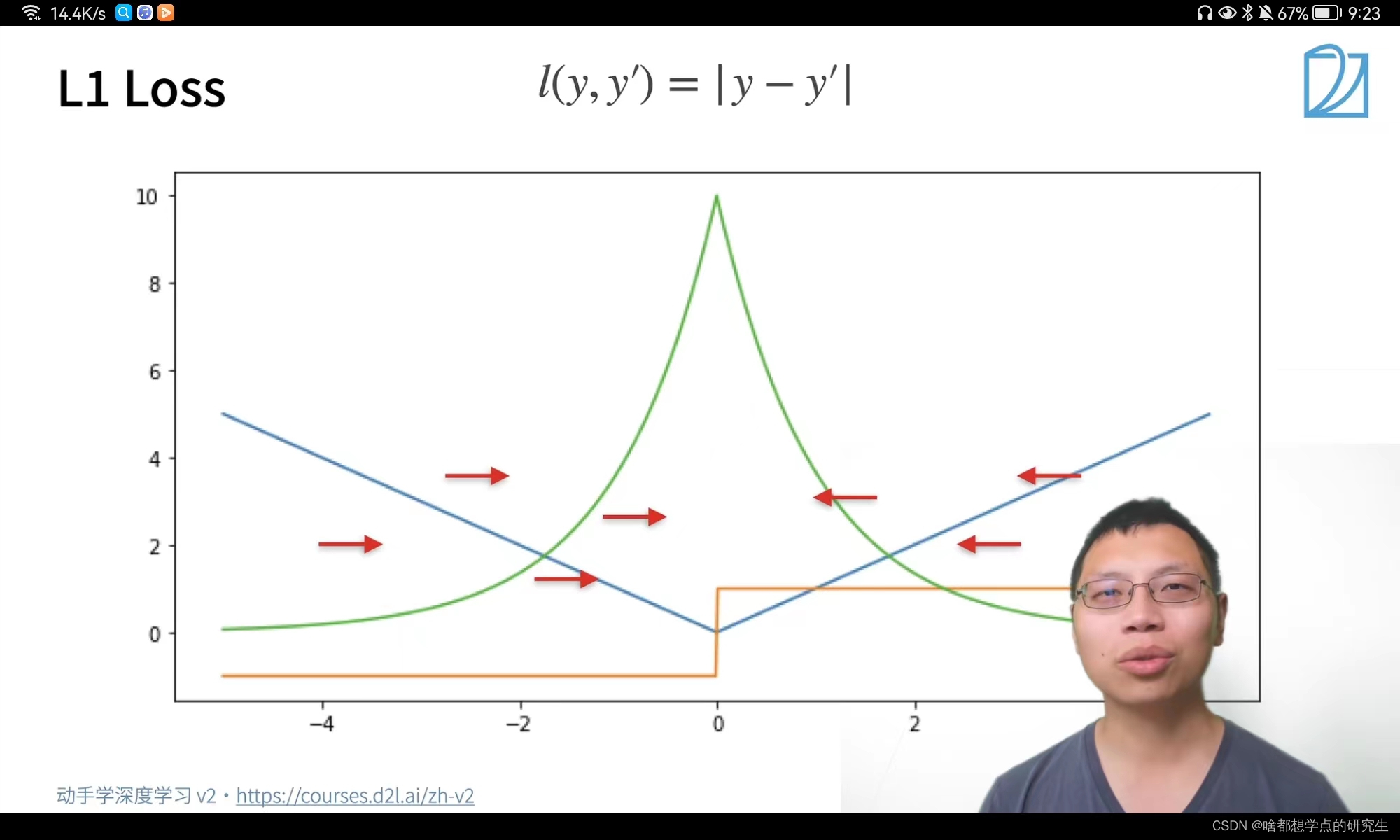
?当预测和我们的真实值隔的比较远的时候,我们的梯度永远是常数,提高系统的稳定性;0点处不可导,优化到末期是系统将变得不稳定。
Huber's Robust Loss:
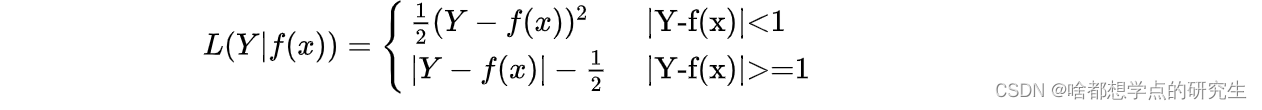
?huber损失是平方损失和绝对损失的综合,它克服了平方损失和绝对损失的缺点,不仅使损失函数具有连续的导数,而且利用MSE梯度随误差减小的特性,可取得更精确的最小值。尽管huber损失对异常点具有更好的鲁棒性,但是,它不仅引入了额外的参数,而且选择合适的参数比较困难,这也增加了训练和调试的工作量。
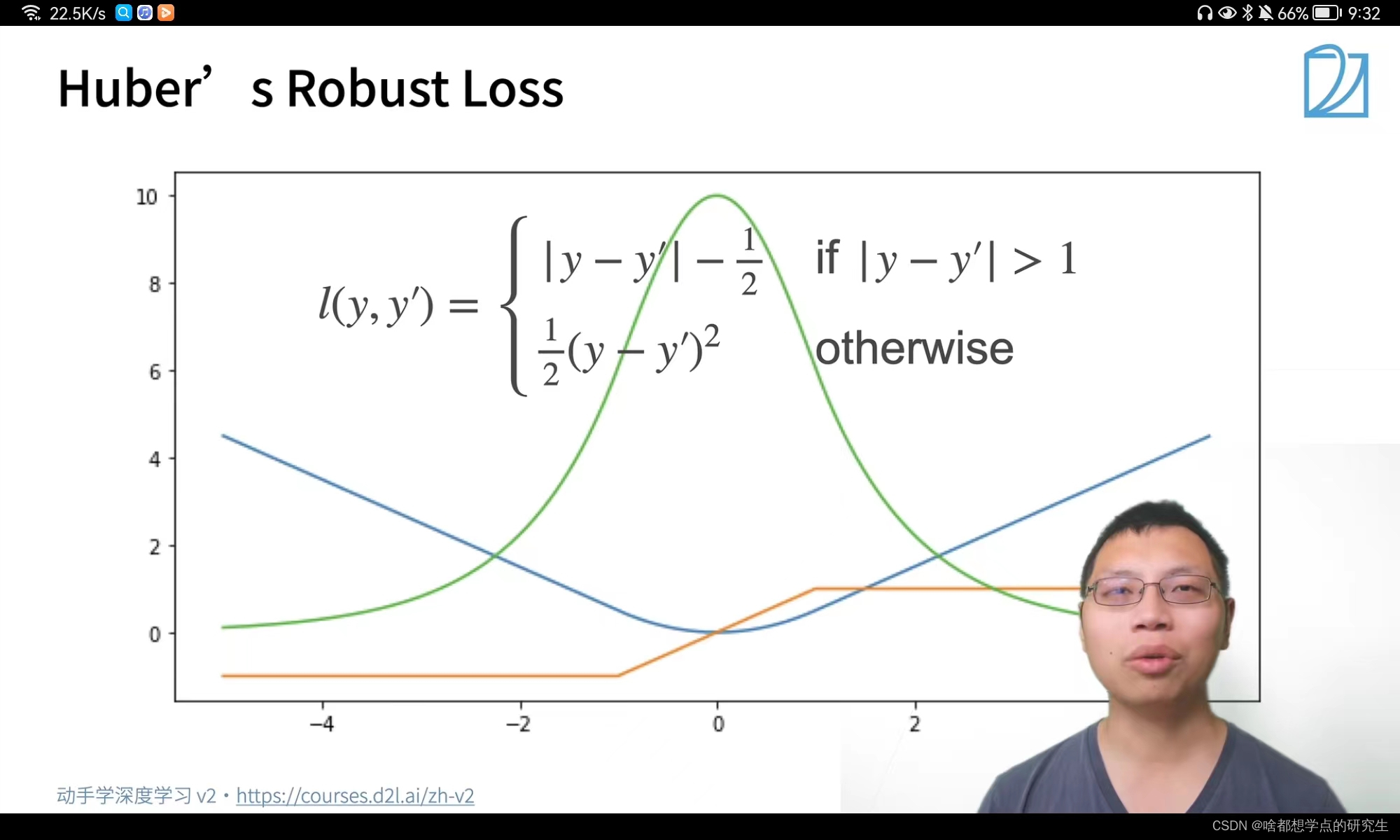
Huber's Robust Loss:图中蓝色是Huber's Robust Loss损失函数;?绿色为Huber's Robust Loss的似然函数;橙色为Huber's Robust Loss的梯度函数。
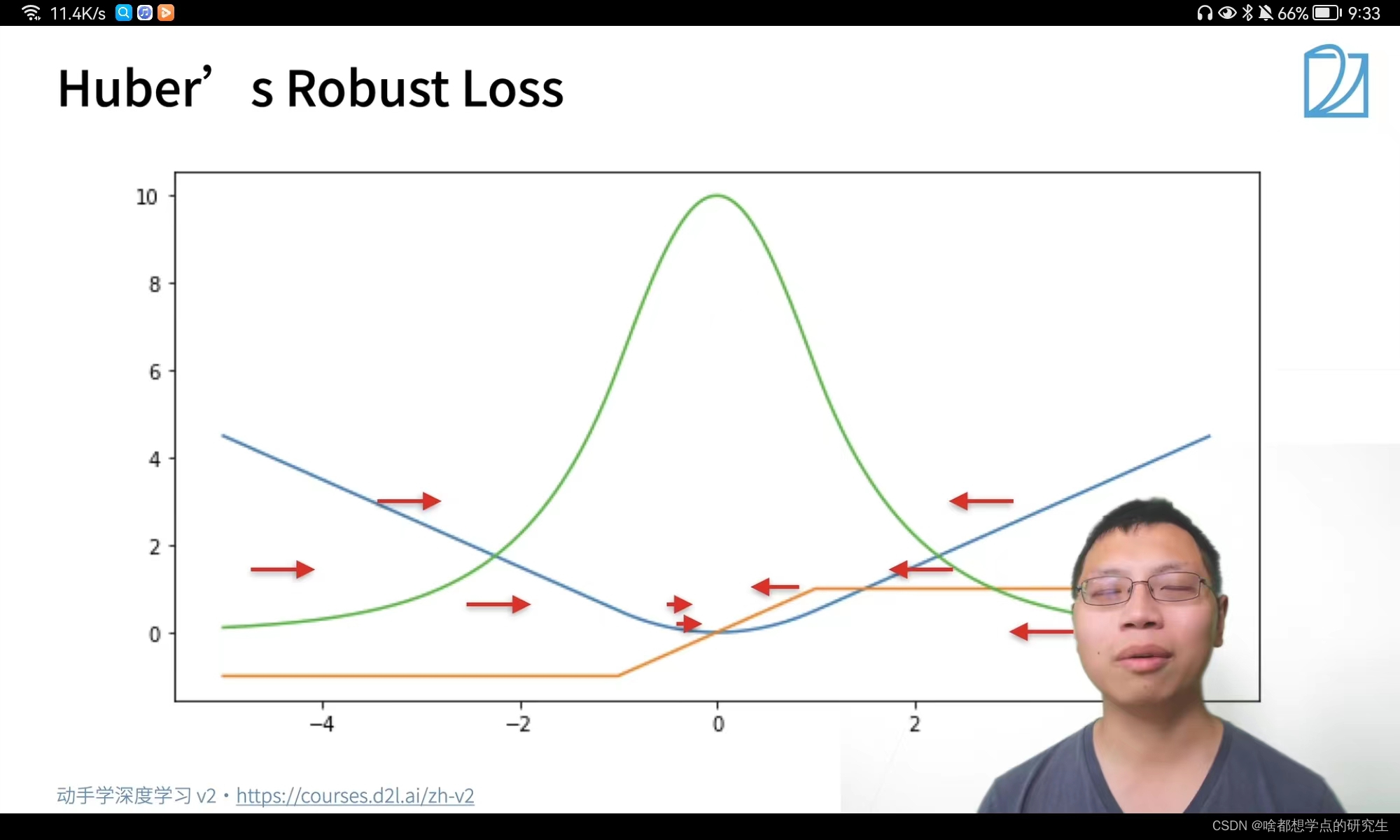
?图中所示,当预测值与真实值距离较远的时候,Huber's Robust Loss损失函数可以以一个恒定的梯度进行梯度下降;当预测值与真实值较近的时候,Huber's Robust Loss损失函数可以较小的梯度进行梯度下降。
图片来源于:李沐动手学深度学习哔哩哔哩教程
