[人工智能] 图神经网络学习(一)-GCN及其应用

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 图神经网络学习(一)-GCN及其应用 -> 正文阅读

[人工智能]图神经网络学习(一)-GCN及其应用

内容提要：GCN背景简介+torch_geometric库安装+GCN处理Cora数据集

1.图神经网络

1.1 概念

原有的卷积神经网络主要用来解决欧式空间中的数据（数据规整，形状固定），例如图像数据。

无法应对非欧式空间中的数据，例如图数据。

但是神经网络是规整的计算方式，所以图神经网络的目标就是，如何去用规整的神经网络去处理不规整的图数据。

1.2 应用场景

非欧数据的场景很多，如：社交网络，计算机网络，病毒传播路径，交通运输网络(地铁网络)，食物链，粒子网络(物理学家描述基本粒子生存的关系，有点类似家谱)，说到家谱，家谱也是，(生物)神经网络(神经网络本来就是生物学术语，现在人工神经网络ANN太多，鸠占鹊巢了)，基因控制网络，分子结构，知识图谱，推荐系统，论文引用网络等等。这些场景的非欧数据用图(Graph)来表达是最合适的，但是，经典的深度学习网络(ANN,CNN,RNN)却难以处理这些非欧数据，于是，图神经网络(GNN)应运而生，GNN以图作为输入，输出各种下游任务的预测结果。

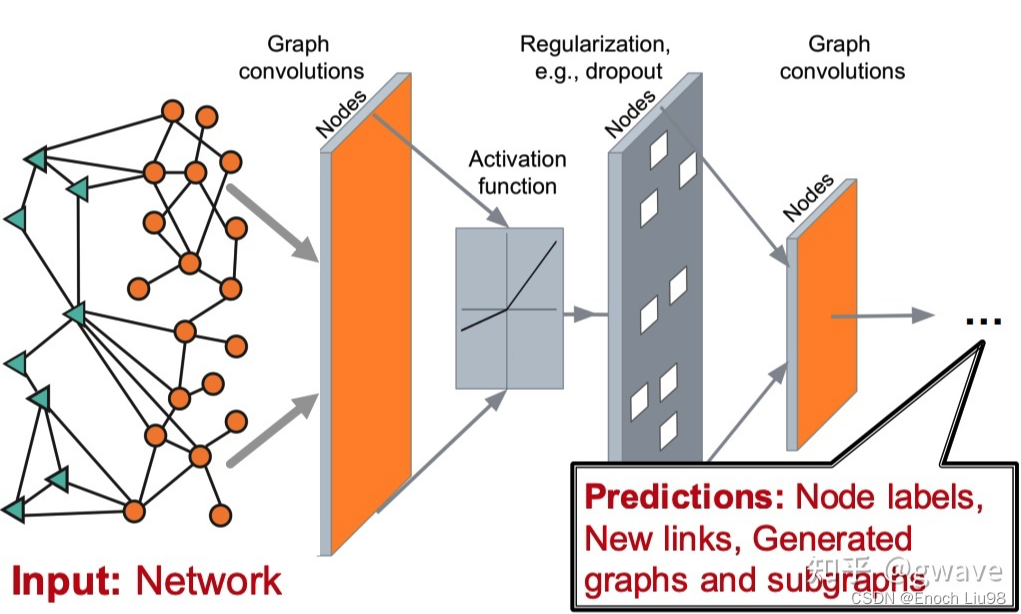
下游任务包括但不限于：

节点分类：预测某一节点的类型
边预测：预测两个节点之间是否存在边
社区预测：识别密集连接的节点所形成的簇
网络相似性: 两个(子)网络是否相似

2.GCN

2.1?图神经网络中层的概念

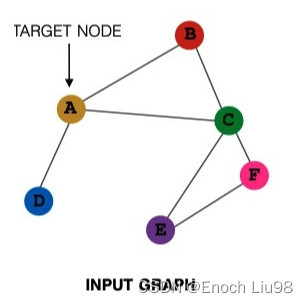
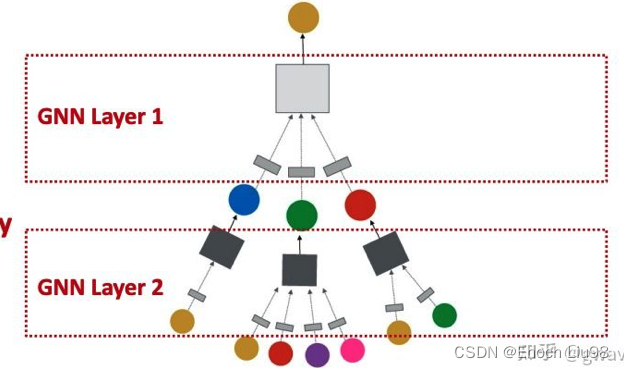
?传统神经网络中是存在层的概念的，而在图神经网络中，层就代表从当前节点，是采用n跳的结果进行更新，这里的n就是层的数目，1跳就是用该节点临近的节点进行更新。

2.2?每一层的运算

每一层的计算其实可以看成一个矩阵相乘的运算，当前节点在当前层的嵌入等于它的邻居节点以及它本身的加权和，这个权值可以使用矩阵的形式表示（邻接矩阵），而节点的嵌入也可以使用矩阵的形式表示，所以最终可以把该运算转换成了一个矩阵相乘运算。?

2.3 举例

问题标号：

A:邻接矩阵（当有边存在，则为1，无边存在，则为0）

X:节点特征

D:度矩阵（度矩阵是对角矩阵，对角线表示了每个节点存在几个邻居，其余位置均为0）

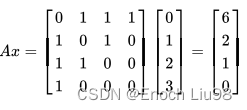
结果向量中的6表示节点0的三个相邻节点的值和和，2表示节点1的两个相邻节点的和，以此类推。

你可能发现，节点0存在3个邻居，而节点3只有1个邻居，上面的矩阵乘法会导致邻居多的节点，在消息交换后的值倾向于比较大，这样不太合理，以均值代替求和更合适，这就是Aggregation Function = Mean的情况，一种实现这种均值消息交换的方法是使用度矩阵(Degree Matrix)。

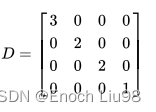
A去除以D

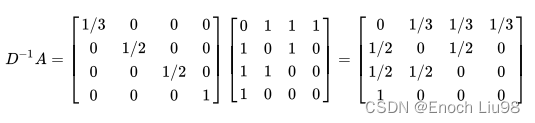
注意到每行的和都等于1，第1行表示节点0有3条边，与节点2，3，4相连，故都是1/3；第4行表示节点3只有1条边与节点0相连，故为1。

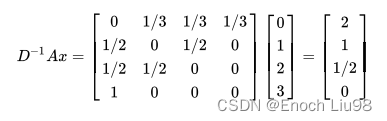
但是这种安排，只考虑了邻居，而忽略了节点自己（A的对角线均为0），假设每个节点都有一条自指的边，则原来的邻接矩阵就变成了：

另外在实际应用中，对于度矩阵的应用，常常采用对称归一化，即：

最终的GCN公式为：

2.4 bonus

上面我们假设边的权重为1，权重也可以是不为1的的其他静态值，或者动态权重，那就是基于注意力的GAT了。?

3.torch_geometric库安装

3.1 简介?

torch_geometric（Pytorch Geometric）库是Pytorch中的图神经网络库，具体的使用方式和pytorch的平常使用没有区别，下面介绍它的安装方式

3.2 安装步骤

安装顺序：cuda->pytorch->torch_geometric

第一步：安装cuda（有gpu）+pytorch

第二步：安装torch_geometric

推荐在官网上安装torch-geometric

torch-geometric官网
在这里插入图片描述

?注：这里不推荐在已有的python环境中安装，会出现奇怪的bug，这里推荐新建一个虚拟环境进行安装。

4.GCN处理Cora数据集

4.1 Cora数据集介绍

Cora数据集由2708篇机器学习领域的论文构成，每个样本点都是一篇论文，这些论文被分成7个类别。

4.2 数据集读取

# %%
# 数据加载
dataset = Planetoid(root="data/Cora", name="Cora")
print(dataset.num_classes)

?4.3 数据探索

# %%
# 数据转换
CoraNet = to_networkx(dataset.data)
CoraNet = CoraNet.to_undirected()
Node_class = dataset.data.y.data.numpy()
print(Node_class)

# %%
# 查看每个节点度的情况
Node_degree = pd.DataFrame(data=CoraNet.degree, columns=["Node", "Degree"])
Node_degree = Node_degree.sort_values(by=["Degree"], ascending=False)
Node_degree = Node_degree.reset_index(drop=True)
Node_degree.iloc[0:30, :].plot(x="Node", y="Degree", kind="bar", figsize=(10, 7))
plt.xlabel("Node", size=12)
plt.ylabel("Degree", size=12)
plt.show()

在可视化数据连接时，使用张量数据格式并不方便，我们这里使用torch_geometric库中的to_networkx函数，可以将Data格式转换成networks库中有向图的图数据，随后再进行可视化。

然后将节点的度信息转化为pandas的格式，进行绘图的结果如下：

# %%
# 绘制分布图
pos = nx.spring_layout(CoraNet)  # 网络图中节点的布局方式
nodecolor = ['red', 'blue', 'green', 'yellow', 'peru', 'violet', 'cyan']  # 颜色
nodelabel = np.array(list(CoraNet.nodes))  # 节点
plt.figure(figsize=(16, 12))

# %%
for ii in np.arange(len(np.unique(Node_class))):
    nodelist = nodelabel[Node_class == ii]  # 对应类别的节点
    print(nodelist, ii)
    nx.draw_networkx_nodes(CoraNet, pos, nodelist=list(nodelist),
                           node_size=50, node_color=nodecolor[ii],
                           alpha=0.8)
nx.draw_networkx_edges(CoraNet, pos, width=1, edge_color="black")
plt.show()

在这里，主要是对于数据的分布进行查看，其中Node_class为每个节点对应的类别，这里不好理解的主要是np.arange(len(np.unique(Node_class))，这句主要是为了根据类别数获得对应的类别向量（例如，原来的类别数为7，则可获得[0,1,2,3,4,5,6]这样的类别向量）

最终绘图的结果如下图所示，这里是先绘制点，再绘制边：

我们这里的处理方法主要是使用半监督学习，这里只使用前140个样本对应的类别标签，而其他的节点虽然参与图卷积的计算，但是不会使用其类别标签进行监督。

下面对这140个样本进行可视化

# %%
#  可视化训练集节点分布
nodecolor = ['red', 'blue', 'green', 'yellow', 'peru', 'violet', 'cyan']  # 颜色
nodelabel = np.arange(0,140)
Node_class = dataset.data.y.data.numpy()[0:140]

for ii in np.arange(len(np.unique(Node_class))):
    nodelist = nodelabel[Node_class == ii]
    nx.draw_networkx_nodes(CoraNet, pos, nodelist=list(nodelist),
                           node_size=50, node_color=nodecolor[ii],
                           alpha=0.8)

plt.show()

4.4 网络构建和训练?

# %%
# 构建一个网络模型类
class GCNnet(torch.nn.Module):
    def __init__(self, input_feature, num_classes):
        super(GCNnet, self).__init__()
        self.input_feature = input_feature  # 输入数据中，每个节点的特征数量
        self.num_classes = num_classes
        self.conv1 = GCNConv(input_feature, 32)
        self.conv2 = GCNConv(32, num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = self.conv2(x, edge_index)
        return F.softmax(x, dim=1)

使用torch_geometric.nn模块中的GCNConv类，可以完成图卷积的操作，十分简单，而且输入只需要指定，节点的输入特征数和最终目标特征数即可，在这里需要注意的是，在forward函数中，需要传入边的信息，也就是edge_index

# %%
input_feature = dataset.num_node_features  # 节点对应的特征数
num_classes = dataset.num_classes  # 类别数目
mygcn = GCNnet(input_feature, num_classes)
print(mygcn)

上面为网络初始化部分。

# %%
device = torch.device("cpu")
model = mygcn.to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
train_loss_all = []
val_loss_all = []
model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.cross_entropy(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()
    train_loss_all.append(loss.data.numpy())

    loss = F.cross_entropy(out[data.val_mask], data.y[data.val_mask])
    val_loss_all.append(loss)

    if epoch % 20 ==0:
        print("epoch",epoch,train_loss_all[-1],val_loss_all[-1])

训练部分中，只有前140个样本是训练集，也就是我们在做半监督学习，我们把整个数据集作为一个完整的batch进行训练。在优化的时候，只使用训练集中的数据,最终训练的结果如下：

绘制loss曲线?

# %%
# 可视化损失函数
plt.figure(figsize=(10,6))
plt.plot(train_loss_all, "ro-", label="Train loss")
plt.plot(val_loss_all, "bs-", label="Val loss")
plt.legend()
plt.grid()
plt.xlabel("epoch", size=13)
plt.ylabel("Loss", size=13)
plt.show()

# %%
# 计算测试集上的准确率
model.eval()
_, pred = model(data).max(dim=1)
correct = float(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / data.test_mask.sum().item()
print(acc)

最终的准确率为0.81

4.5 隐藏层特征可视化

# %%
# 进行TSNE姜维
from sklearn.manifold import TSNE
x_tsne = TSNE(n_components=2).fit_transform(dataset.data.x.data.numpy())
plt.figure()
ax1 = plt.subplot(1, 1, 1)
X = x_tsne[:, 0]
Y = x_tsne[:, 1]
ax1.set_xlim([min(X), max(X)])
ax1.set_ylim([min(Y), max(Y)])
for ii in range(x_tsne.shape[0]):
    text = dataset.data.y.data.numpy()[ii]
    ax1.text(X[ii], Y[ii], str(text), fontsize=5,
             bbox=dict(boxstyle="round", facecolor=plt.cm.Set1(text), alpha=0.7))
ax1.set_xlabel("TSNE Feature 1", size=13)
ax1.set_ylabel("TSNE Feature 2", size=13)
plt.show()

对原来的1433维的向量采用TSNE进行降维，并绘制对应的曲线。?

????????

# %%
# 使用钩子函数，查看网络中间的输出特征
activation = {}  # 保存不同层的输出


def get_activation(name):
    def hook(model, input, output):  # 使用闭包
        activation[name] = output.detach()

    return hook


model.conv1.register_forward_hook(get_activation("conv1"))
_ = model(data)
conv1 = activation["conv1"].data.numpy()
print(conv1.shape)

为了可视化图神经网络的中间特征，我们这里需要使用钩子函数，钩子函数是一种闭包函数。

# %%
# 使用钩子函数，查看网络中间的输出特征
activation = {}  # 保存不同层的输出


def get_activation(name):
    def hook(model, input, output):  # 使用闭包
        activation[name] = output.detach()

    return hook


model.conv1.register_forward_hook(get_activation("conv1"))
_ = model(data)
conv1 = activation["conv1"].data.numpy()
print(conv1.shape)

# %%
conv1_tsne = TSNE(n_components=2).fit_transform(conv1)
plt.figure(figsize=(12, 8))
ax1 = plt.subplot(1, 1, 1)
X = conv1_tsne[:, 0]
Y = conv1_tsne[:, 1]
ax1.set_xlim([min(X), max(X)])
ax1.set_ylim([min(Y), max(Y)])
for ii in range(conv1_tsne.shape[0]):
    text = dataset.data.y.data.numpy()[ii]
    ax1.text(X[ii], Y[ii], str(text), fontsize=5,
             bbox=dict(boxstyle="round", facecolor=plt.cm.Set1(text), alpha=0.7))
ax1.set_xlabel("TSNE Feature 1", size=13)
ax1.set_ylabel("TSNE Feature 2", size=13)
plt.show()

由此图可见，数据分类已初见雏形。

4.6 与SVM，LP分类结果对比

# %%
from sklearn.metrics import accuracy_score
from sklearn.svm import SVC
from sklearn.semi_supervised import _label_propagation
X = dataset.data.x.data.numpy()
Y = dataset.data.y.data.numpy()
train_mask = dataset.data.train_mask.data.numpy()
test_mask = dataset.data.test_mask.data.numpy()
train_x = X[0:140, :]
train_y = Y[train_mask]
test_x = X[1708:2708, :]
test_y = Y[test_mask]

svmmodel = SVC()
svmmodel.fit(train_x,train_y)
prelab = svmmodel.predict(test_x)
print(accuracy_score(test_y,prelab))

SVM方法，最终在测试集上的准确率为0.56，由于没有考虑节点之间的关系，所以准确率不如图神经网络的准确率.

# %%
# LP
X = dataset.data.x.data.numpy()
Y = dataset.data.y.data.numpy()
train_mask = dataset.data.train_mask.data.numpy()
test_mask = dataset.data.test_mask.data.numpy()
train_y = Y.copy()
train_y[test_mask == True] = -1
test_y = Y[test_mask]
lp_model = _label_propagation.LabelPropagation(kernel="knn", n_neighbors=3)
lp_model.fit(X, train_y)
prelab = lp_model.transduction_
print(accuracy_score(Y[test_mask], prelab[test_mask]))

LP方法，是一种半监督方法，最终的准确率为0.45.

4.7 代码汇总版

import torch
import torch.nn.functional as F
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid
from torch_geometric.utils import to_networkx
import networkx as nx

# %%
# 数据加载
dataset = Planetoid(root="data/Cora", name="Cora")
print(dataset.num_classes)

# %%
# 数据探索
CoraNet = to_networkx(dataset.data)
CoraNet = CoraNet.to_undirected()
Node_class = dataset.data.y.data.numpy()
print(Node_class)

# %%
# 查看每个节点度的情况
Node_degree = pd.DataFrame(data=CoraNet.degree, columns=["Node", "Degree"])
Node_degree = Node_degree.sort_values(by=["Degree"], ascending=False)
Node_degree = Node_degree.reset_index(drop=True)
Node_degree.iloc[0:30, :].plot(x="Node", y="Degree", kind="bar", figsize=(10, 7))
plt.xlabel("Node", size=12)
plt.ylabel("Degree", size=12)
plt.show()

# %%
# 绘制分布图
pos = nx.spring_layout(CoraNet)  # 网络图中节点的布局方式
nodecolor = ['red', 'blue', 'green', 'yellow', 'peru', 'violet', 'cyan']  # 颜色
nodelabel = np.array(list(CoraNet.nodes))  # 节点
plt.figure(figsize=(16, 12))

# %%
for ii in np.arange(len(np.unique(Node_class))):
    nodelist = nodelabel[Node_class == ii]  # 对应类别的节点
    print(nodelist, ii)
    nx.draw_networkx_nodes(CoraNet, pos, nodelist=list(nodelist),
                           node_size=50, node_color=nodecolor[ii],
                           alpha=0.8)
nx.draw_networkx_edges(CoraNet, pos, width=1, edge_color="black")
plt.show()

# %%
#  可视化训练集节点分布
nodecolor = ['red', 'blue', 'green', 'yellow', 'peru', 'violet', 'cyan']  # 颜色
nodelabel = np.arange(0, 140)
Node_class = dataset.data.y.data.numpy()[0:140]

for ii in np.arange(len(np.unique(Node_class))):
    nodelist = nodelabel[Node_class == ii]
    nx.draw_networkx_nodes(CoraNet, pos, nodelist=list(nodelist),
                           node_size=50, node_color=nodecolor[ii],
                           alpha=0.8)

plt.show()


# %%
# 构建一个网络模型类
class GCNnet(torch.nn.Module):
    def __init__(self, input_feature, num_classes):
        super(GCNnet, self).__init__()
        self.input_feature = input_feature  # 输入数据中，每个节点的特征数量
        self.num_classes = num_classes
        self.conv1 = GCNConv(input_feature, 32)
        self.conv2 = GCNConv(32, num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = self.conv2(x, edge_index)
        return F.softmax(x, dim=1)


# %%
input_feature = dataset.num_node_features  # 节点对应的特征数
num_classes = dataset.num_classes  # 类别数目
mygcn = GCNnet(input_feature, num_classes)
print(mygcn)

# %%
data = dataset[0].train_mask
print(data)
data = data[data == True]
print(len(data))

# %%
device = torch.device("cpu")
model = mygcn.to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
train_loss_all = []
val_loss_all = []
model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.cross_entropy(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()
    train_loss_all.append(loss.data.numpy())

    loss = F.cross_entropy(out[data.val_mask], data.y[data.val_mask])
    val_loss_all.append(loss.data.numpy())

    if epoch % 20 == 0:
        print("epoch", epoch, train_loss_all[-1], val_loss_all[-1])

# %%
# 可视化损失函数
plt.figure(figsize=(10, 6))
plt.plot(train_loss_all, "ro-", label="Train loss")
plt.plot(val_loss_all, "bs-", label="Val loss")
plt.legend()
plt.grid()
plt.xlabel("epoch", size=13)
plt.ylabel("Loss", size=13)
plt.show()

# %%
# 计算测试集上的准确率
model.eval()
_, pred = model(data).max(dim=1)
correct = float(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / data.test_mask.sum().item()
print(acc)

# %%
# 进行TSNE姜维
from sklearn.manifold import TSNE

x_tsne = TSNE(n_components=2).fit_transform(dataset.data.x.data.numpy())
plt.figure(figsize=(12, 8))
ax1 = plt.subplot(1, 1, 1)
X = x_tsne[:, 0]
Y = x_tsne[:, 1]
ax1.set_xlim([min(X), max(X)])
ax1.set_ylim([min(Y), max(Y)])
for ii in range(x_tsne.shape[0]):
    text = dataset.data.y.data.numpy()[ii]
    ax1.text(X[ii], Y[ii], str(text), fontsize=5,
             bbox=dict(boxstyle="round", facecolor=plt.cm.Set1(text), alpha=0.7))
ax1.set_xlabel("TSNE Feature 1", size=13)
ax1.set_ylabel("TSNE Feature 2", size=13)
plt.show()

# %%
# 使用钩子函数，查看网络中间的输出特征
activation = {}  # 保存不同层的输出


def get_activation(name):
    def hook(model, input, output):  # 使用闭包
        activation[name] = output.detach()

    return hook


model.conv1.register_forward_hook(get_activation("conv1"))
_ = model(data)
conv1 = activation["conv1"].data.numpy()
print(conv1.shape)

# %%
conv1_tsne = TSNE(n_components=2).fit_transform(conv1)
plt.figure(figsize=(12, 8))
ax1 = plt.subplot(1, 1, 1)
X = conv1_tsne[:, 0]
Y = conv1_tsne[:, 1]
ax1.set_xlim([min(X), max(X)])
ax1.set_ylim([min(Y), max(Y)])
for ii in range(conv1_tsne.shape[0]):
    text = dataset.data.y.data.numpy()[ii]
    ax1.text(X[ii], Y[ii], str(text), fontsize=5,
             bbox=dict(boxstyle="round", facecolor=plt.cm.Set1(text), alpha=0.7))
ax1.set_xlabel("TSNE Feature 1", size=13)
ax1.set_ylabel("TSNE Feature 2", size=13)
plt.show()


# %%
# SVM
from sklearn.metrics import accuracy_score
from sklearn.svm import SVC
from sklearn.semi_supervised import _label_propagation
X = dataset.data.x.data.numpy()
Y = dataset.data.y.data.numpy()
train_mask = dataset.data.train_mask.data.numpy()
test_mask = dataset.data.test_mask.data.numpy()
train_x = X[0:140, :]
train_y = Y[train_mask]
test_x = X[1708:2708, :]
test_y = Y[test_mask]

svmmodel = SVC()
svmmodel.fit(train_x,train_y)
prelab = svmmodel.predict(test_x)
print(accuracy_score(test_y,prelab))

# %%
# LP
X = dataset.data.x.data.numpy()
Y = dataset.data.y.data.numpy()
train_mask = dataset.data.train_mask.data.numpy()
test_mask = dataset.data.test_mask.data.numpy()
train_y = Y.copy()
train_y[test_mask == True] = -1
test_y = Y[test_mask]
lp_model = _label_propagation.LabelPropagation(kernel="knn", n_neighbors=3)
lp_model.fit(X, train_y)
prelab = lp_model.transduction_
print(accuracy_score(Y[test_mask], prelab[test_mask]))