[人工智能] RANSAC算法与原理（一）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> RANSAC算法与原理（一） -> 正文阅读

[人工智能]RANSAC算法与原理（一）

算法介绍

首先我们从Random sample consensus - Wikipedia上找到RANSAC原理的介绍。

RANSAC算法的中文名称是随机抽样一致算法(Random Sample Consenus)，简单的说，通过RANSAC算法，我们将数据分为inliers和outliers,inliers是对于模型拟合有效的点，也称之为内点；outliers是对于模型拟合无效的点，也就是错误的数据点，称之为外点。而我们在使用观测数据拟合模型的过程中，外点的存在对于使用数据拟合模型是有害的，那么我们该如何剔除这些外点呢？RANSAC算法就是能够剔除外点的一个迭代性的算法。

举例

下图所示就是RANSAC算法的作用：剔除外点，使模型估计更加准确，参考Robust line model estimation using RANSAC — skimage v0.19.2 docs (scikit-image.org)

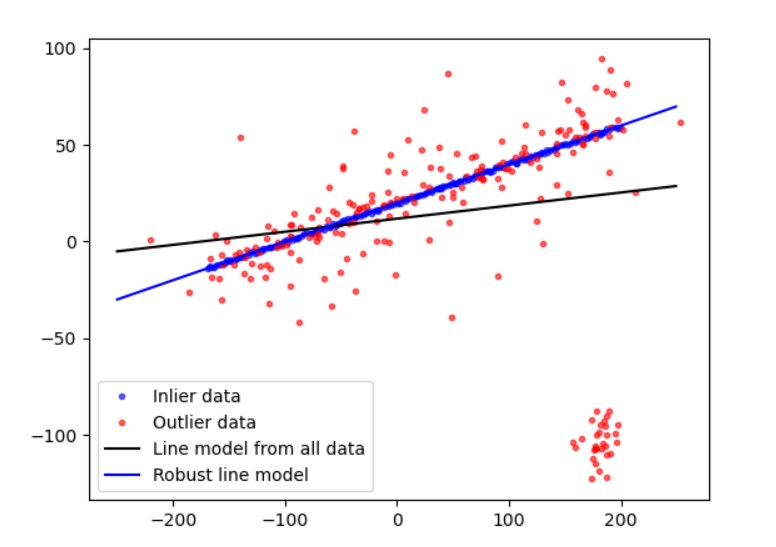
屏幕截图 2022-05-24 092807

算法的基本思想和流程

算法的实现流程：

选择出估计模型的最小数据样本（对于二维和三维直线拟合来说，确定一条直线最少需要2个点；对于三维平面拟合来说，确定一个三维平面最少需要3个点）
使用这个最小的数据样本，算出拟合的模型。（也就是直线方程或者平面方程）
将所有的模型带入这个拟合的模型，计算出内点的数量。（数据点和拟合的模型的误差在一定阈值范围内的数据点的数量）
比较当前模型和之前迭代的得到的最好的模型的内点数量（内点数量越多，模型越好），记录最大的内点数的模型参数和内点数量。
重复1-4步，直到达到迭代终止条件（例如达到最大迭代数、内点数量达到迭代终止条件）

迭代次数的推导

假设内点在数据中所占的比例为 $t$
$t=\frac{n_{inliers}}{n_{inliers}+n_{outliers}}$
如果我们每次迭代都需要 $N$ 个点，那么每次迭代至少有一个外点的概率是：
$P_{1}=1-t^N$
那么我们如果迭代 $k$ 次，所有的 $k$ 次迭代都至少有一个外点的概率为 $P_{1}^{k}$ ，那么这 $k$ 次迭代，能够采样到正确的 $N$ 个内点去计算模型的概率就是上述概率的补集。
$P=1-P_{1}^{k}=1-(1-t^{N})^{k}$
通过上式，我们可以求得
$k=\frac{log(1-P)}{log(1-t^{N})}$
注意：内点的概率 $t$ 是一个先验值，如果我们一开始不知道这个先验值 $t$ ，可以采用自适应迭代的方法，用当前的内点的比值来当成 $t$ 来估算迭代的次数。然后通过不断迭代，内点的比值也逐渐增大，再用新的更大的内点比值去代替 $t$ 的值；对于 $P$ 来说，一般会取一个定值0.99，等式（4）可以看出，当 $P$ 不变时， $t$ 越大， $k$ 越小， $t$ 越小， $k$ 越大。

算法的实现

Given:
    data – A set of observations.
    model – A model to explain observed data points.
    n – Minimum number of data points required to estimate model parameters.
    k – Maximum number of iterations allowed in the algorithm.
    t – Threshold value to determine data points that are fit well by model.
    d – Number of close data points required to assert that a model fits well to data.

Return:
    bestFit – model parameters which best fit the data (or null if no good model is found)

iterations = 0
bestFit = null
bestErr = something really large

while iterations < k do
    maybeInliers := n randomly selected values from data
    maybeModel := model parameters fitted to maybeInliers
    alsoInliers := empty set
    for every point in data not in maybeInliers do
        if point fits maybeModel with an error smaller than t
             add point to alsoInliers
        end if
    end for
    if the number of elements in alsoInliers is > d then
        // This implies that we may have found a good model
        // now test how good it is.
        betterModel := model parameters fitted to all points in maybeInliers and alsoInliers
        thisErr := a measure of how well betterModel fits these points
        if thisErr < bestErr then
            bestFit := betterModel
            bestErr := thisErr
        end if
    end if
    increment iterations
end while

return bestFit

python代码实现

以下代码参考scikit-image/fit.py at v0.19.2 · scikit-image/scikit-image (github.com)，也就是skimage的源码。

def _dynamic_max_trials(n_inliers, n_samples, min_samples, probability):
    
     if n_inliers == 0:
        return np.inf

    if probability == 1:
        return np.inf

    if n_inliers == n_samples:
        return 1

    nom = math.log(1 - probability)
    denom = math.log(1 - (n_inliers / n_samples) ** min_samples)

    return int(np.ceil(nom / denom))



def ransac(data, model_class, min_samples, residual_threshold,
   			is_data_valid=None, is_model_valid=None,
           max_trials=100, stop_sample_num=np.inf, stop_residuals_sum=0,
           stop_probability=1, random_state=None, initial_inliers=None):
    
    best_inlier_num = 0
    best_inlier_residuals_sum = np.inf
    best_inliers = []
    validate_model = is_model_valid is not None
    validate_data = is_data_valid is not None

    random_state = np.random.default_rng(random_state)

    # in case data is not pair of input and output, male it like it
    if not isinstance(data, (tuple, list)):
        data = (data, )
    num_samples = len(data[0])

    if not (0 < min_samples < num_samples):
        raise ValueError(f"`min_samples` must be in range (0, {num_samples})")

    if residual_threshold < 0:
        raise ValueError("`residual_threshold` must be greater than zero")

    if max_trials < 0:
        raise ValueError("`max_trials` must be greater than zero")

    if not (0 <= stop_probability <= 1):
        raise ValueError("`stop_probability` must be in range [0, 1]")

    if initial_inliers is not None and len(initial_inliers) != num_samples:
        raise ValueError(
            f"RANSAC received a vector of initial inliers (length "
            f"{len(initial_inliers)}) that didn't match the number of "
            f"samples ({num_samples}). The vector of initial inliers should "
            f"have the same length as the number of samples and contain only "
            f"True (this sample is an initial inlier) and False (this one "
            f"isn't) values.")

    # for the first run use initial guess of inliers
    spl_idxs = (initial_inliers if initial_inliers is not None
                else random_state.choice(num_samples, min_samples,
                                         replace=False))

    # estimate model for current random sample set
    model = model_class()

    for num_trials in range(max_trials):
        # do sample selection according data pairs
        samples = [d[spl_idxs] for d in data]

        # for next iteration choose random sample set and be sure that
        # no samples repeat
        spl_idxs = random_state.choice(num_samples, min_samples, replace=False)

        # optional check if random sample set is valid
        if validate_data and not is_data_valid(*samples):
            continue

        success = model.estimate(*samples)
        # backwards compatibility
        if success is not None and not success:
            continue

        # optional check if estimated model is valid
        if validate_model and not is_model_valid(model, *samples):
            continue

        residuals = np.abs(model.residuals(*data))
        # consensus set / inliers
        inliers = residuals < residual_threshold
        residuals_sum = residuals.dot(residuals)

        # choose as new best model if number of inliers is maximal
        inliers_count = np.count_nonzero(inliers)
        if (
            # more inliers
            inliers_count > best_inlier_num
            # same number of inliers but less "error" in terms of residuals
            or (inliers_count == best_inlier_num
                and residuals_sum < best_inlier_residuals_sum)):
            best_inlier_num = inliers_count
            best_inlier_residuals_sum = residuals_sum
            best_inliers = inliers
            dynamic_max_trials = _dynamic_max_trials(best_inlier_num,
                                                     num_samples,
                                                     min_samples,
                                                     stop_probability)
            if (best_inlier_num >= stop_sample_num
                    or best_inlier_residuals_sum <= stop_residuals_sum
                    or num_trials >= dynamic_max_trials):
                break

    # estimate final model using all inliers
    if any(best_inliers):
        # select inliers for each data array
        data_inliers = [d[best_inliers] for d in data]
        model.estimate(*data_inliers)
        if validate_model and not is_model_valid(model, *data_inliers):
            warn("Estimated model is not valid. Try increasing max_trials.")
    else:
        model = None
        best_inliers = None
        warn("No inliers found. Model not fitted")

    return model, best_inliers