引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不使用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

我们前面学习过n-gram语言模型，但是n-gram模型中的n不能太大，这限制了它的应用。本文我们学习如何基于前馈神经网络来构建语言模型。

前馈网络语言模型

我们知道语言模型是基于前面的上下文单词来预测下一个单词。

前馈网络语言模型¹的架构图如上图所示。分为四层：

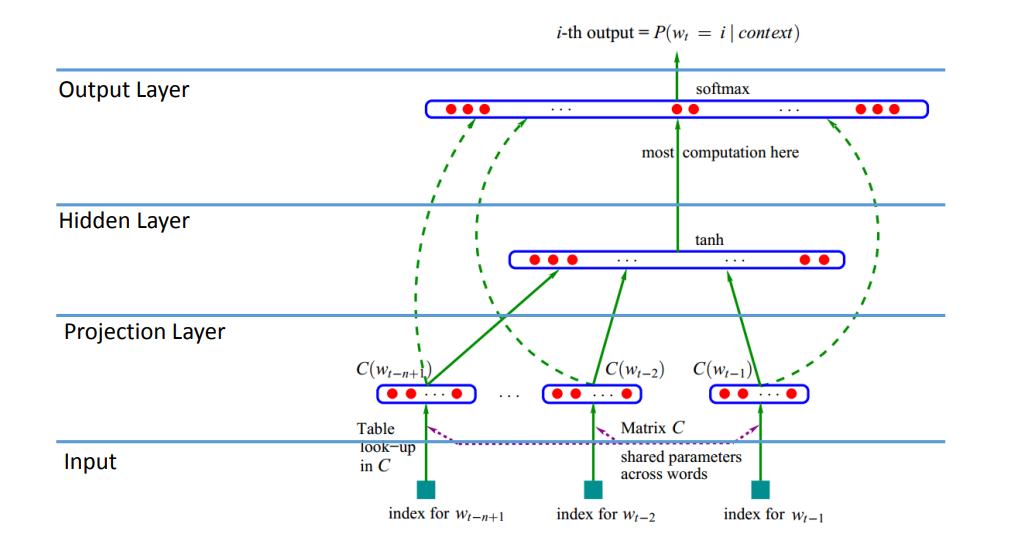
输入层(Input Layer)
投影层(Projection Layer)
隐藏层(Hidden Layer)
输出层(Output Layer)

输入是每个单词的独热编码。类似N-gram，神经概率语言模型也有一个窗口。根据投影层(嵌入层)得到窗口大小的嵌入向量。然后拼接这些嵌入向量，经过一个隐藏层，激活函数是 $\text{tanh}$ 。然后经过 $\text{softmax}$ 得到给定上下文窗口下预测下一个单词的概率分布。

我们具体来看一看。

前向推理

和Word2vec一样，也有时间步的概念。在每个时间步，假设词典大小为 $∣ V ∣$ ，给定窗口大小。我们使用长度为 $∣ V ∣$ 的独热编码表示 $N$ 个之前的单词。

假设 $N = 3$ ,我们这里就有三个独热编码。

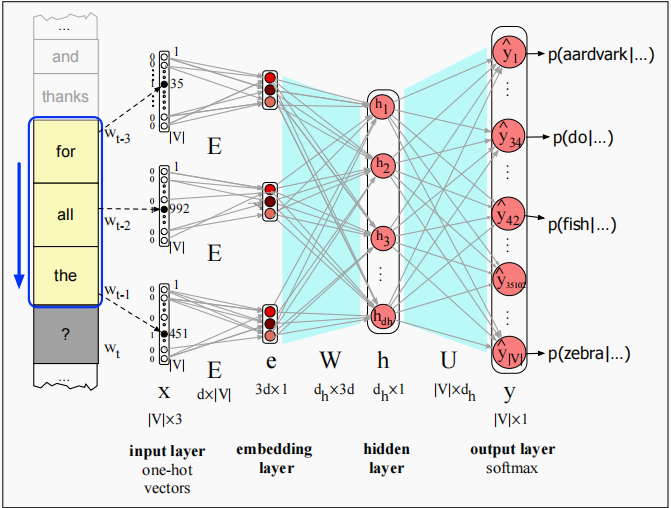
如上图所示，在时间步 $t$ ，都有3个独热编码，大小为 $\times 3$ ，分别乘上嵌入矩阵 $\in \Bbb R^{d \times |V|}$ 。得到3个大小为 $\times 1$ 的嵌入向量。

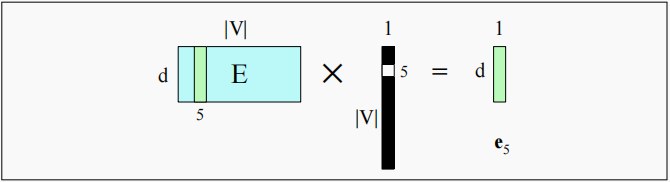
假设某个独热编码只有索引为5处的元素为1，那么乘上嵌入矩阵后，相当于选择了嵌入矩阵的第5列，这种操作我们已经在word2vec中见过了。

然后我们把这三个嵌入向量拼接起来得到 $\in \Bbb R ^{3d \times 1}$ ，这就是投影层的结果。然后嵌入向量 $e$ 乘以一个权重矩阵 $\in \Bbb R^{d_h \times 3d}$ ， $d_h$ 为隐藏层大小，得到隐藏状态 $\in \Bbb R^{d_h \times 1}$ 。然后经过 $\tanh$ 激活函数，维度不变。最后乘以矩阵 $\in \Bbb R^{|V| \times d_h}$ ，得到维度为 $\times 1$ 的向量，经过 $\text{softmax}$ 得到了整个词典内所有单词的概率分布。

总结一下，上面例子中使用的算法如下：

从嵌入矩阵 $E$ 中选择三个嵌入向量：给定三个之前的单词，查看索引，得到3个独热编码向量，然后乘上矩阵 $E$ 。假设 $w_{t-3}$ 代表索引35处单词for的独热编码，乘上矩阵 $E$ ，得到 $\times 1$ 的嵌入向量。即索引 $i$ 处的独热编码经过 $Ex_i=e_i$ 。然后拼接3个单词嵌入，得到 $3d \times 1$ 的嵌入 $e$ 。
乘上 $W$ ：我们再乘上 $W$ (可能加上对应偏置)，经过激活函数( $\tanh$ 或 $\text{ReLU}$ )得到隐藏向量 $h$ 。
乘上 $U$ ： $h$ 接着乘上 $U$ ，将其维度扩展成和词典大小一致。
应用 $\text{softmax}$ ：在经过 $\text{softmax}$ ，得到了词典中每个单词作为下一个单词的概率 $P(w_t=i|w_{t-1},w_{t-2},w_{t-3})$ 。

其对应的公式为：
$\begin{aligned} e &= [E_{x_{t-3}}; E_{x_{t-2}};E_{x_{t-1}}] \\ h &= σ(We+b) \\ z &= Uh \\ \hat y &= \text{softmax}(z) \end{aligned} \tag 1$
我们用 $;$ 来表示拼接。我们已经知道了前向推理的过程，那么如何定义损失函数呢？

损失函数

显然，这是一个多分类问题。一般使用交叉熵损失函数。

首先，当我们有多类时，我们需要将 $y$ 和 $\hat y$ 都表示为向量。假设我们处理硬分类，即只有一个正确类别。真实标签 $y$ 就是一个个数为 $K$ 的独热编码，如果真实类别为 $c$ ，那么只有 $y_c=1$ 。而我们的分类器会产生同样 $K$ 个元素的估计向量 $\hat y$ ，每个元素 $\hat y_k$ 代表估计概率 $p(y_k = 1|x)$ 。

对于单个样本的损失函数就是 $K$ 个输出类别概率的负对数之和，通过类别对应的真实概率 $y_k$ 加权：
$L_{CE}(\hat y, y) = - \sum^K_{k=1} y_k \log \hat y_k \tag 2$
我们可以进一步地简化该公式。我们先使用 $\Bbb{1}\{\}$ 重写，如果括号内的条件为真那么返回 $1$ ，否则返回 $0$ ?。那么可以得到：
$L_{CE}(\hat y,y) = -\sum_{k=1}^K \Bbb{1}\{y_k=1\} \log \hat y_k \tag 3$
只有真实类别 $y_k=1$ 的时候才不为 $0$ ?。换言之，交叉熵损失就是简单的负对数正确类别的输出概率，我们称为负对数似然损失：
$L_{CE}(\hat y,y) = -\log \hat y_c \quad \text{$c$是正确类别} \tag 4$
通过softmax函数展开，并有 $K$ 个类别时：
$L_{CE}(\hat y,y) = -\log \frac{\text{exp}(z_c)}{\sum_{j=1}^K \exp(z_j)} \quad \text{$c$是正确类别} \tag 5$
下面来看如何训练前馈网络语言模型。

训练

我们需要的参数 $\theta=E,W,U,b$ 。

训练的目的是得到嵌入矩阵 $E$ ，我们就可以像使用word2vec中的嵌入矩阵一样，使用该矩阵 $E$ 来获取每个单词的嵌入向量。

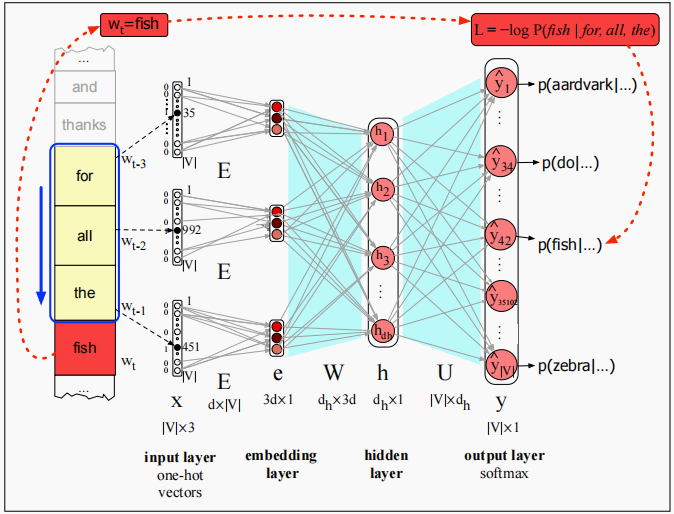
还是上面的例子，给定上下文for all the来预测下一个单词fish的概率。

如上小节所介绍的，我们使用交叉熵(负对数似然)损失：
$L_{CE}(\hat y,y) = -\log \hat y_c \quad \text{$c$是正确类别} \tag 6$
对于语言模型来说，类别就是词典中的所有单词，所以 $\hat y_c$ 意味着模型分配给正确单词 $w_t$ 的概率：
$L_{CE} = -\log p(w_t|w_{t-1},\cdots,w_{t-n+1}) \tag 7$
我们希望模型分配给正确单词的概率越高越好，通过最小化上面的损失来更新参数 $\theta$ 。

代码实现

数据集

数据还是西游记数据集。

数据集下载 → 提取码：nap4

class NGramDataset(Dataset):
    def __init__(self, corpus, vocab, window_size=4):
        self.data = []
        self.bos = vocab[BOS_TOKEN]
        self.eos = vocab[EOS_TOKEN]
        for sentence in tqdm(corpus, desc="Dataset Construction"):
            # 插入句首句尾符号
            sentence = [self.bos] + sentence + [self.eos]
            if len(sentence) < window_size:
                continue
            for i in range(window_size, len(sentence)):
                # 模型输入：长为context_size的上文
                context = sentence[i - window_size:i]
                # 模型输出：当前词
                target = sentence[i]
                self.data.append((context, target))

        self.data = np.asarray(self.data)

    def __len__(self):
        return len(self.data)

    def __getitem__(self, i):
        return self.data[i]

    def collate_fn(self, examples):
        # 从独立样本集合中构建batch输入输出
        inputs = Tensor([ex[0] for ex in examples])
        targets = Tensor([ex[1] for ex in examples])
        return inputs, targets

模型

创建前馈网络语言模型类²，参数主要包括词嵌入层、词嵌入到隐藏层、隐藏层到输出层。

class FeedForwardNNLM(nn.Module):
    def __init__(self, vocab_size, embedding_dim, window_size, hidden_dim):
        # 单词嵌入E : 输入层 -> 嵌入层
        self.embeddings = nn.Embedding(vocab_size, embedding_dim)
        # 词嵌入层 -> 隐藏层
        self.e2h = nn.Linear(window_size * embedding_dim, hidden_dim)
        #  隐藏层 -> 输出层
        self.h2o = nn.Linear(hidden_dim, vocab_size)

        self.activate = F.relu

    def forward(self, inputs) -> Tensor:
        embeds = self.embeddings(inputs).reshape((inputs.shape[0], -1))
        hidden = self.activate(self.e2h(embeds))
        output = self.h2o(hidden)
        log_probs = F.log_softmax(output, axis=1)
        return log_probs

训练

if __name__ == '__main__':
    embedding_dim = 64
    window_size = 2
    hidden_dim = 128
    batch_size = 1024
    num_epoch = 10
    min_freq = 3  # 保留单词最少出现的次数

    # 读取文本数据，构建FFNNLM训练数据集（n-grams）
    corpus, vocab = load_corpus('../../data/xiyouji.txt', min_freq)
    dataset = NGramDataset(corpus, vocab, window_size)
    data_loader = DataLoader(
        dataset,
        batch_size=batch_size,
        collate_fn=dataset.collate_fn,
        shuffle=True
    )

    # 负对数似然损失函数
    nll_loss = NLLLoss()
    # 构建FFNNLM，并加载至device
    device = cuda.get_device("cuda:0" if cuda.is_available() else "cpu")

    model = FeedForwardNNLM(len(vocab), embedding_dim, window_size, hidden_dim)
    model.to(device)

    optimizer = SGD(model.parameters(), lr=0.001)

    total_losses = []
    for epoch in range(num_epoch):
        total_loss = 0
        for batch in tqdm(data_loader, desc=f"Training Epoch {epoch}"):
            inputs, targets = [x.to(device) for x in batch]
            optimizer.zero_grad()
            log_probs = model(inputs)
            loss = nll_loss(log_probs, targets)
            loss.backward()
            optimizer.step()
            total_loss += loss.item()
        print(f"Loss: {total_loss:.2f}")
        total_losses.append(total_loss)

    # 保存词向量（model.embeddings）
    save_pretrained(vocab, model.embeddings.weight.data, "ffnnlm.vec")