校准曲线图表示的是预测值和实际值的差距,作为预测模型的重要部分,目前很多函数能绘制校准曲线。
一般分为两种,一种是通过Hosmer-Lemeshow检验,把P值分为10等分,求出每等分的预测值和实际值的差距
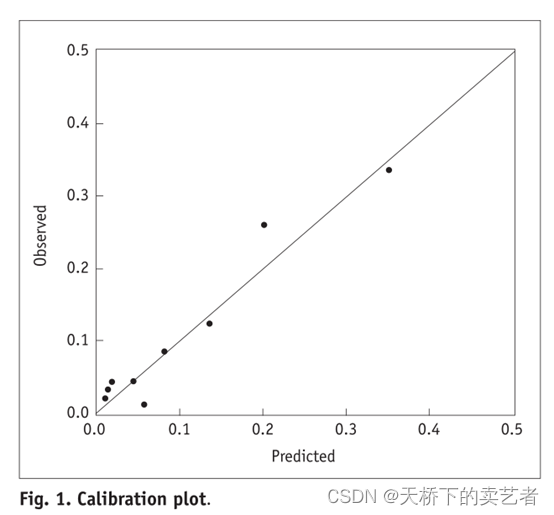
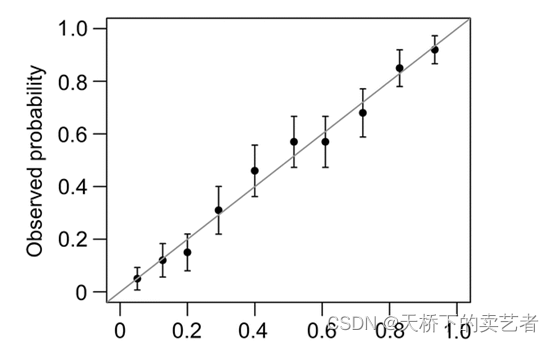
另外一种是calibration函数重抽样绘制连续的校准图
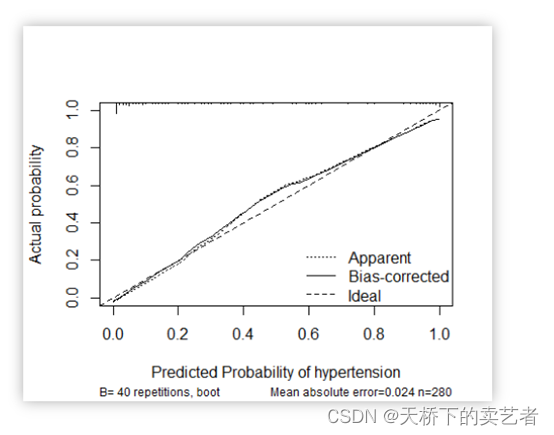
今天我们来演示第一种,手动绘制的好处在于加深你对绘图的理解,而且能个性化的进一步处理图形。第一种绘图本质就是我们的折线图,上一章《R语言绘制带误差和可信区间的折线图》我们已经介绍了怎么绘制折线图,只要求出相关数据就可以了。
我们先导入数据,继续使用我们的早产数据,
library(ggplot2)
library(rms)
bc<-read.csv("E:/r/test/zaochan.csv",sep=',',header=TRUE)
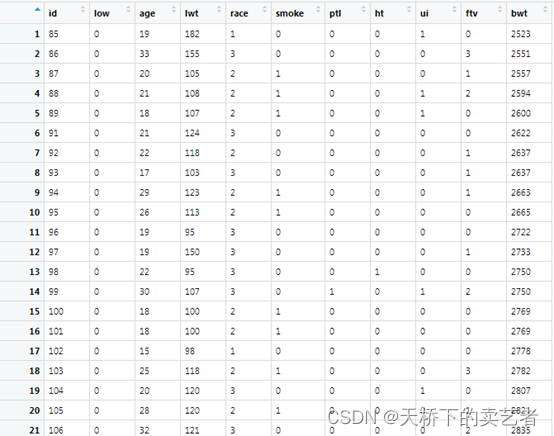
这是一个关于早产低体重儿的数据(公众号回复:早产数据,可以获得该数据),低于2500g被认为是低体重儿。数据解释如下:low 是否是小于2500g早产低体重儿,age 母亲的年龄,lwt 末次月经体重,race 种族,smoke 孕期抽烟,ptl 早产史(计数),ht 有高血压病史,ui 子宫过敏,ftv 早孕时看医生的次数,bwt 新生儿体重数值。
我们先把分类变量转成因子
bc$race<-ifelse(bc$race=="black",1,ifelse(bc$race=="white",2,3))
bc$smoke<-ifelse(bc$smoke=="nonsmoker",0,1)
bc$race<-factor(bc$race)
bc$ht<-factor(bc$ht)
bc$ui<-factor(bc$ui)
建立回归方程
fit<-glm(low ~ age + lwt + race + smoke + ptl + ht + ui + ftv,
family = binomial("logit"),
data = bc)
得出预测概率
pr1 <- predict(fit,type = c("response"))#得出预测概率
p = pr1
使用order函数对P值排序,这里注意一下,order§排的是位置
sor <- order(p)

P值按order来排列
p <- p[sor]
Y值也按order来排列
y = bc[, "low"]
y <- y[sor]
把P值分为10个等分区间
groep <- cut2(p, g = 10)
计算每个等分的P值和Y值
meanpred <- round(tapply(p, groep, mean), 3)
meanobs <- round(tapply(y, groep, mean), 3)
绘图
plot(meanpred, meanobs)
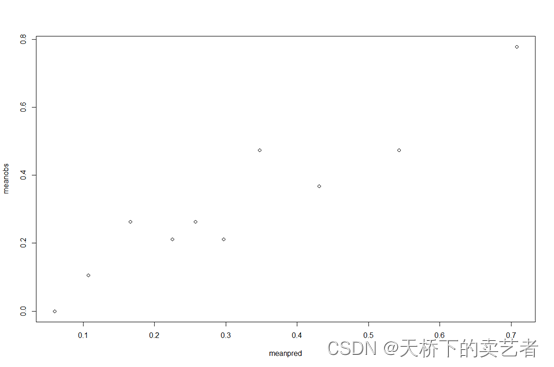
修饰一下,好像稍微好看了点
plot(meanpred, meanobs,xlab = "Predicted risk",
ylab = "Observed risk", pch = 16, ps = 2, xlim = c(0, 1),
ylim = c(0, 1), cex.lab = 1.2, cex.axis = 1.1,
las = 1)
abline(0, 1, col = "grey", lwd = 1, lty = 1)
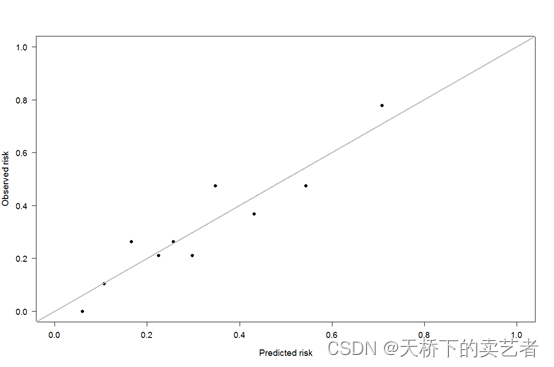
我们还可以和上一篇文章《R语言绘制带误差和可信区间的折线图》一样算出它的标准误,以便进一步计算可信区间
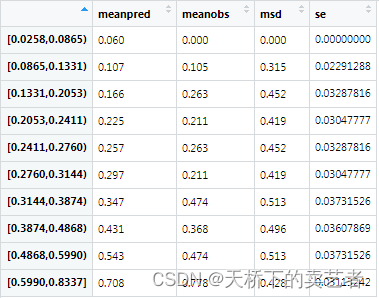
计算可信区间后可以进一步绘图
ggplot(matres, aes(x=meanpred, y=meanobs)) +
geom_errorbar(aes(ymin=meanobs-1.96*se, ymax=meanobs+1.96*se), width=.02)
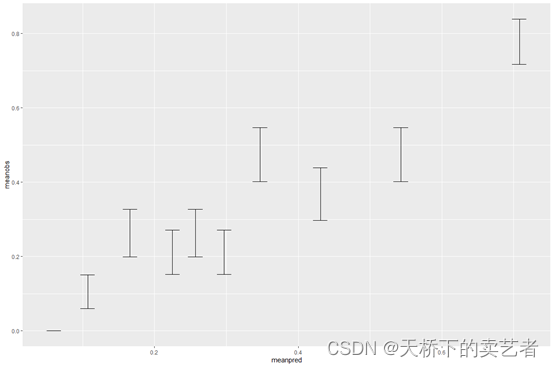
添加对角线
ggplot(matres, aes(x=meanpred, y=meanobs)) +
geom_errorbar(aes(ymin=meanobs-1.96*se, ymax=meanobs+1.96*se), width=.02)+
annotate(geom = "segment", x = 0, y = 0, xend =1, yend = 1)+
expand_limits(x = 0, y = 0) +
scale_x_continuous(expand = c(0, 0)) +
scale_y_continuous(expand = c(0, 0))+
geom_point()+
xlab("预测概率")+
ylab("实际概率")
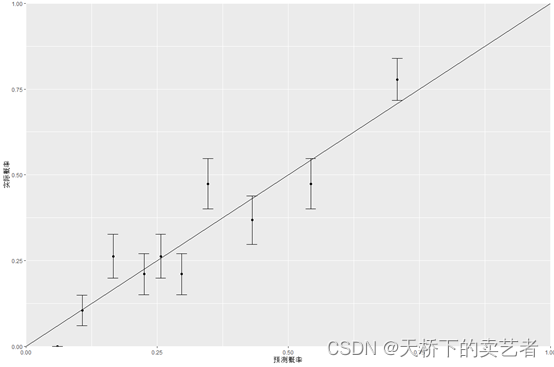
进一步修饰
ggplot(matres, aes(x=meanpred, y=meanobs)) +
geom_errorbar(aes(ymin=meanobs-1.96*se, ymax=meanobs+1.96*se), width=.02)+
annotate(geom = "segment", x = 0, y = 0, xend =1, yend = 1)+
expand_limits(x = 0, y = 0) +
scale_x_continuous(expand = c(0, 0)) +
scale_y_continuous(expand = c(0, 0))+
geom_point(size=3, shape=21, fill="white")+
xlab("预测概率")+
ylab("实际概率")
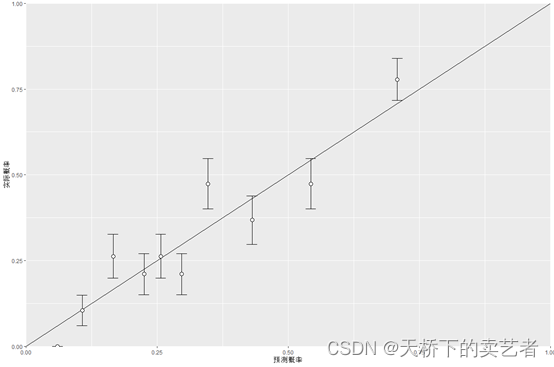
使用PredictABEL包的plotCalibration函数来验证一下我们计算的正确性
library(PredictABEL)
plotCalibration(data = bc,
cOutcome = 2,#结果在第几行就选几
predRisk = pr1,
groups = 10,
rangeaxis = c(0,1))
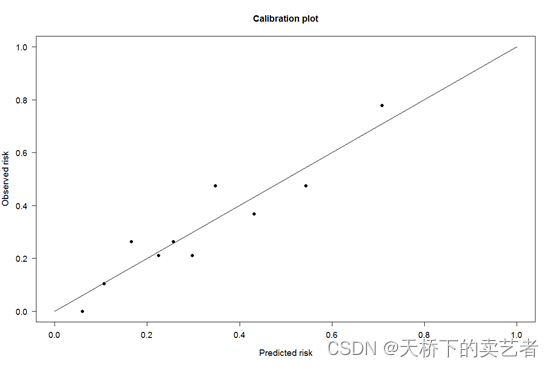
和我们手工计算完全一致,证明我们算得没有问题。目前也比较流行使用重抽样的方法获取可信区间,将在今后章节介绍。OK,本期到此结束。需要全部代码的请公众号回复:代码。
