CNN(卷积神经网络)
Why CNN for image
DNN也可以处理图像,为什么我们用CNN呢?
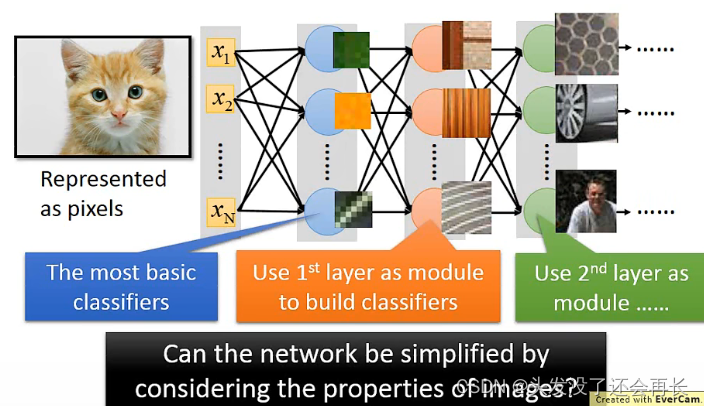
首先,DNN全连接层比较复杂,参数较多,但其中可能有些neuron是不必要的,CNN就是用来简化DNN,基于下面的特征:
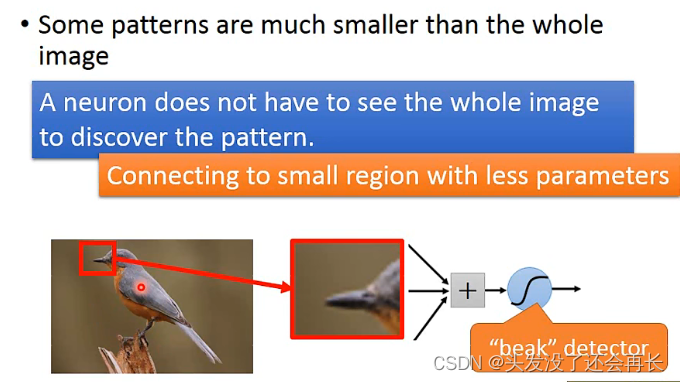
- 有一些模式可能是很小的一部分,不必看整张图片,比如识别一只鸟,如果一个neuron只需要识别鸟嘴,那只要给这个neuron这个图片鸟嘴部分就行了,所以一个neuron只需要连接鸟嘴部分就行,而不是整张图
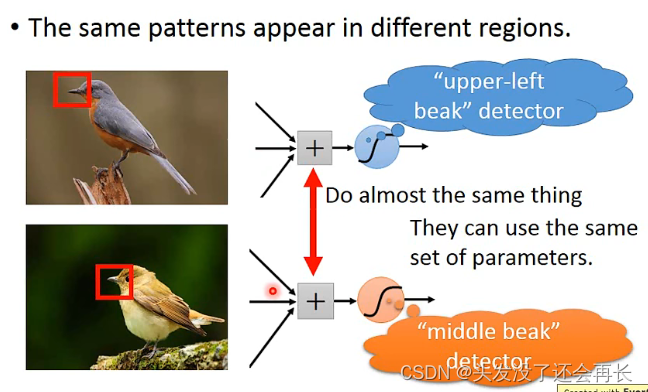
- 相同的模式可能出现在一张图片的不同的部分,但他们的形状是一样的,代表同样的含义,可以用同一个neuron,比如两张图片的鸟嘴,一个在左上角,一个在中间,因为都是鸟嘴,所以不需要两个neuron,只需要一个就可以识别,那就需要一个参数,减少使用的参数的量
3.对图片做下采样,不会改变图中的物体。下采样让图像变小,减少参数
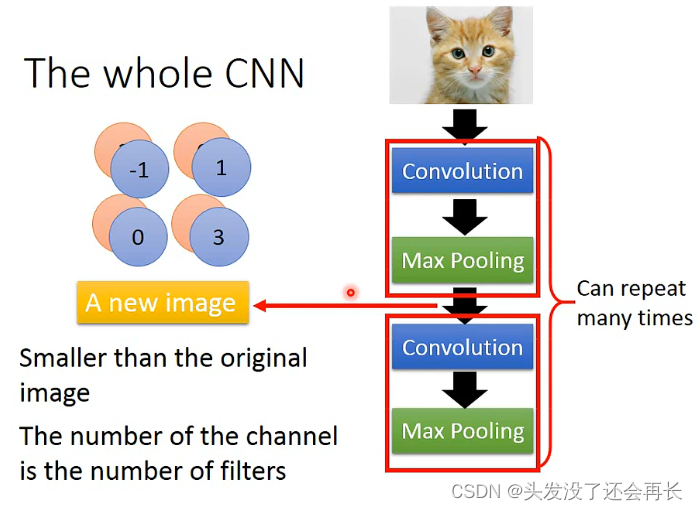
The whole CNN
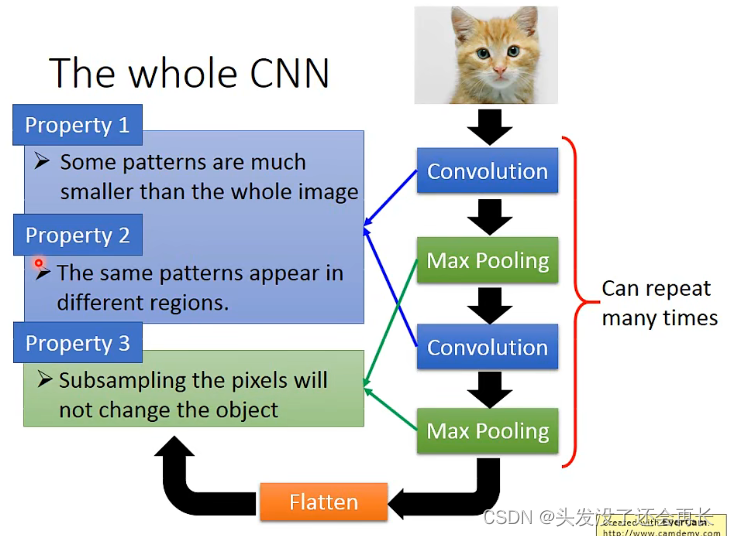
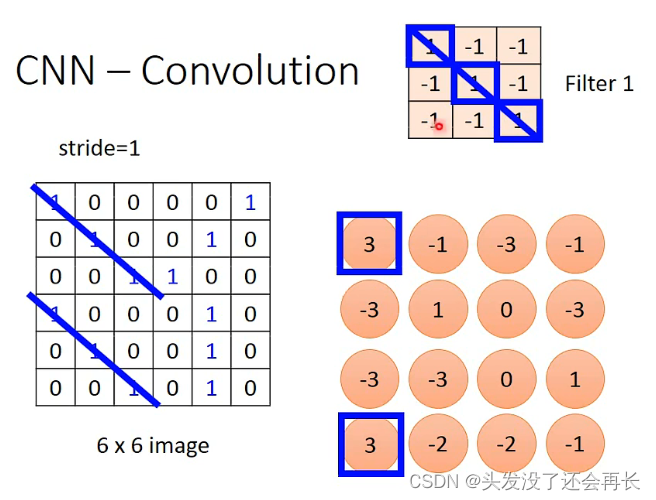
CNN——Convolution
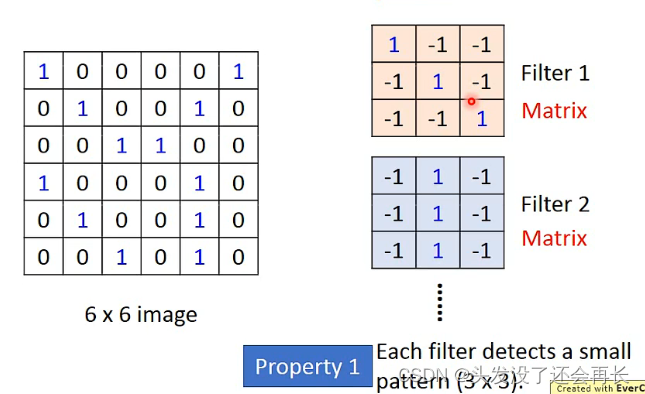
卷积(convolution)操作中有一些过滤器(filter),也被称为卷积核,相当于神经网络中的神经元,需要被学习。
过滤器就是一些矩阵,它负责提取图像中的特征,进行特征映射(feature map)
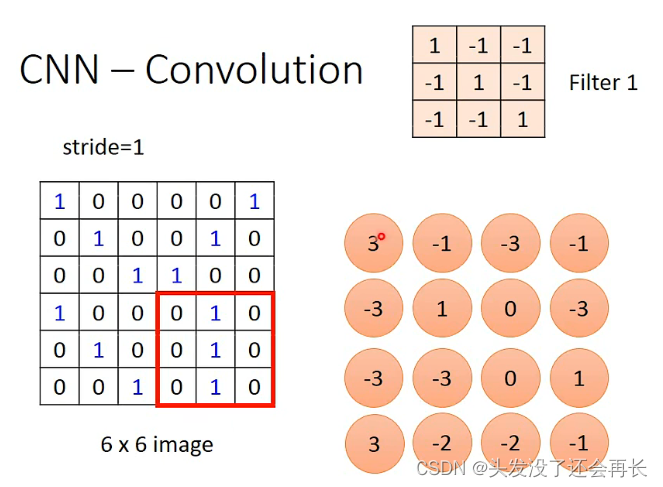
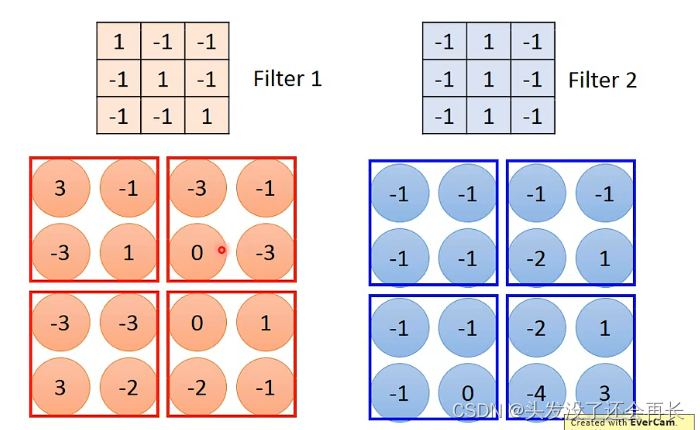
卷积计算其实就是将一个N*N的Filter与原来图像某个N*N大小的部分做内积,可以看成将Filter盖在image的矩阵上面,被盖住的部分和上面Filter对应的格子相乘,比如下面image红色圈住的部分,和Filter做内积,就是1X0+(-1)X1+(-1)X0+(-1)X0+1X0+(-1)X0+(-1)X0+1X1+(-1)X0+(-1)X0+(-1)X1+1X0=-1,如果一个一个的移动,就会得到下面4 x 4的image
观察得到的矩阵可以发现,当Filter的斜对角线是(1,1,1),在原来image出现同样斜对角线为(1,1,1)的地方,在卷积结果的image中就会是最大值,也就是这个Filter想要识别的特征部分,所以对于同样的特征,我们只需要一个Filter就可以侦测出来,并不需要不同的Filter
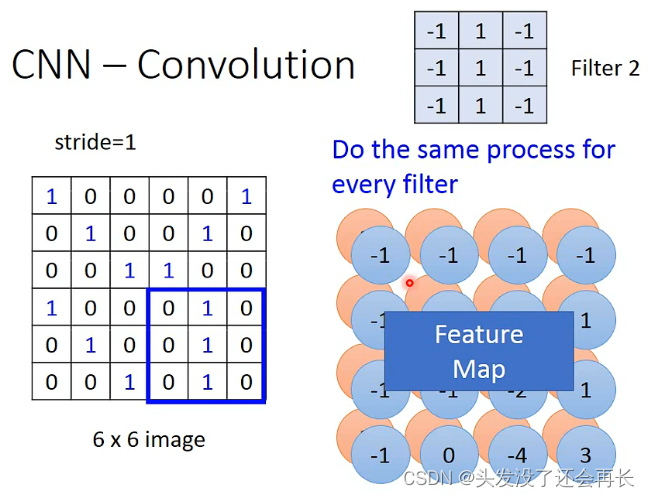
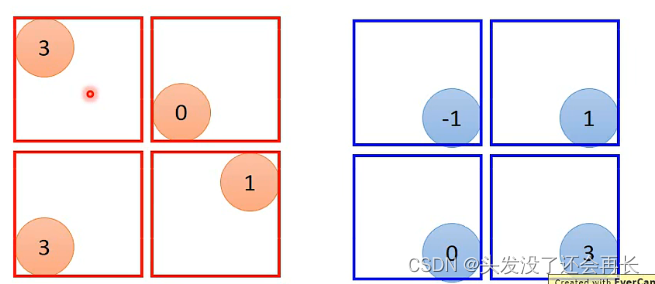
如果还有一个Filter,那么就会再得到一个image,这两个合在一起,就是Feature Map,如果有多个Filter,那么就是多个image合在一起得到特征图,有几个Filter,得到的Map就是多少维的
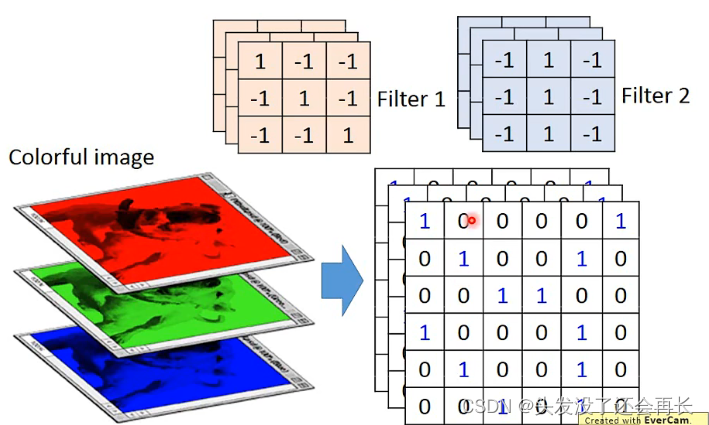
CNN——colorful image
彩色图片就是由rgb组成的,那转化成矩阵就是好几个矩阵叠在一起,对应的Filter也是一样的层数,计算的时候,也是几层一起算
Convolution vs Fully connected
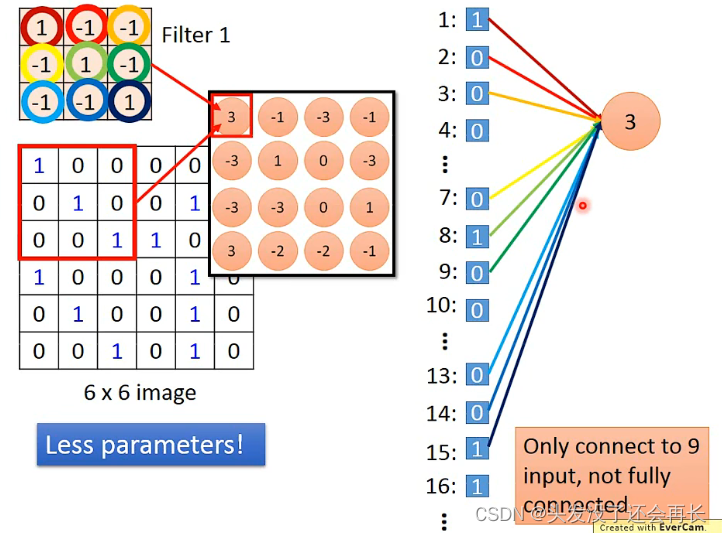
其实CNN的convolution就是全连接的network拿掉一些weight的结果
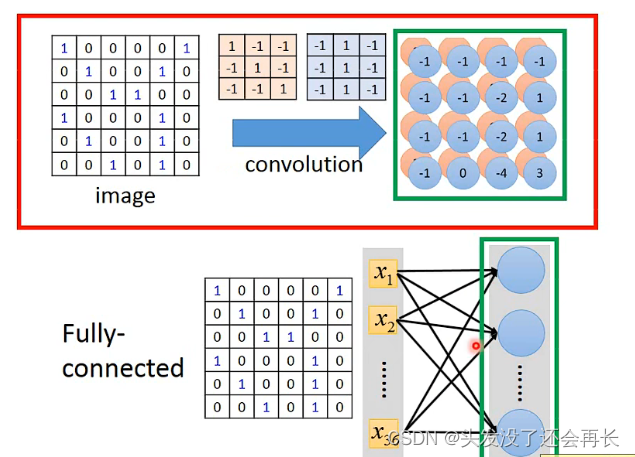
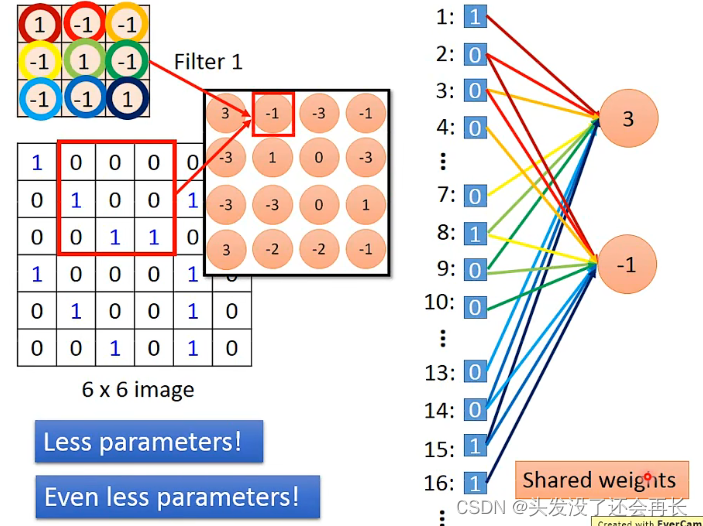
下面的图,右边不同的颜色的线对应Filter的相同颜色的圈圈,表示weight,Filter与6 x 6 image的红色框柱部分相乘就得到3(output),我们将图像从第一行到最后一行展开写成右边的样子,每一个位置都是一个input(像全连接的x1,x2…xn),可以知道,红色框柱的部分对应的位置是1,2,3,7,8,9,13,14,15,这些位置,与3这个neuron相连,也就是3这个neuron只连接了9个input,而在全连接的network,每个neuron要连接6*6=36个input,所以参数变少了!!
如果将Filter往右移动一格,用同样的方法得到内积为-1,将-1作为一个neuron的output,并将它画在右图,它对应的input位置就是2,3,4,8,9,10,14,15,16,因为用的同样的Filter,可以发现这两个neuron用的同样的weight,这样的话,参数比原来更少,因为全连接的network,每一个neuron的weight都是独立的
CNN——Max Pooling
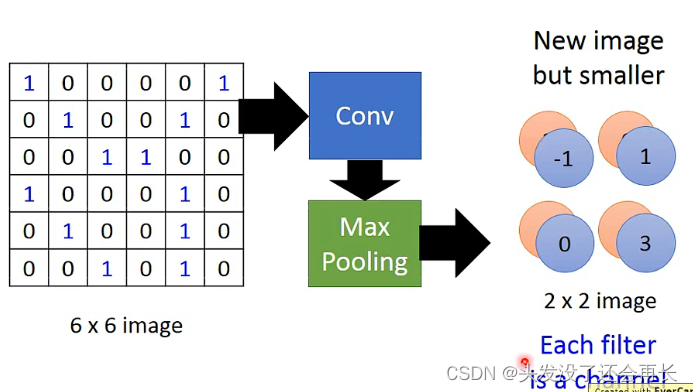
将原来卷积得到的两个image,每四个一组,可以在四个里面取一个最大或者中位数保留下来,将image缩小
假设现在将每一组里面最大的数保留下来
这样的话,就得到了一个2 x 2的两维的image,一个Filter是一个channel
在CNN里,Convolution和Max Pooling可以做很多次
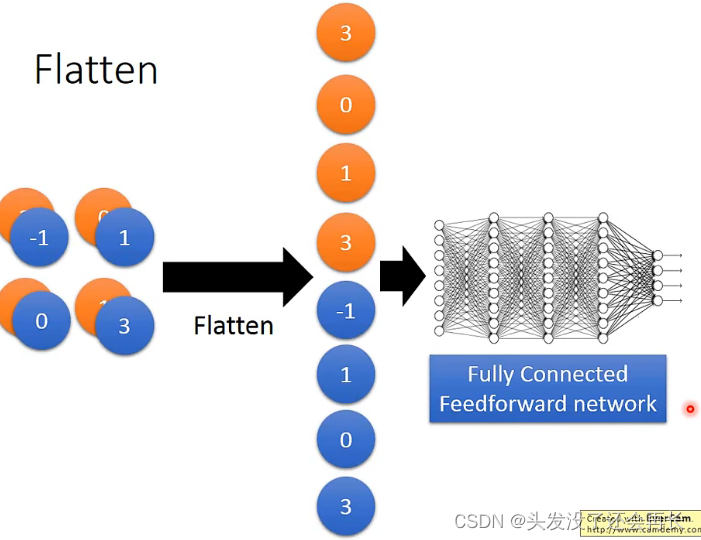
CNN——Flatten
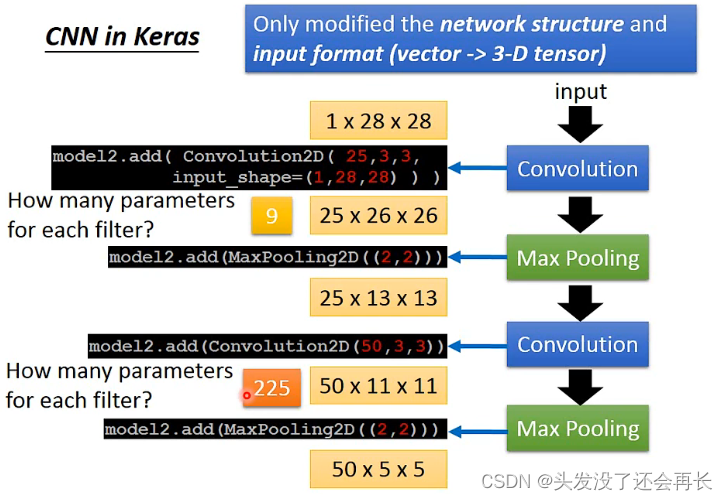
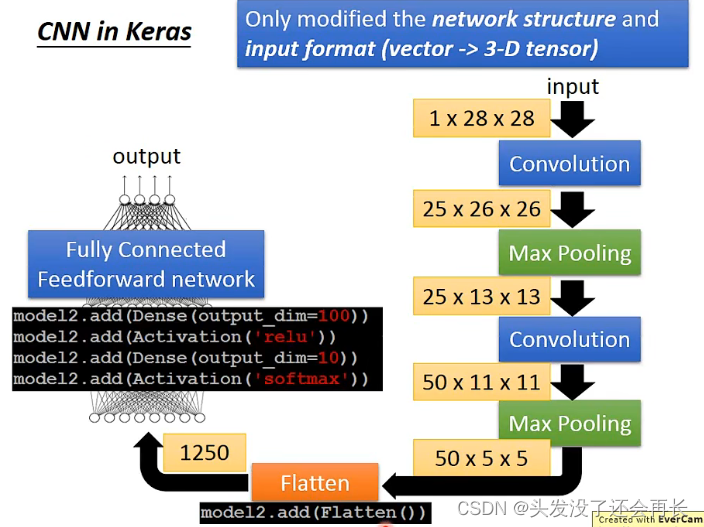
CNN in Keras
输入一个28*28的图像,只有一个颜色,Filter有25个,大小为3*3的,经过两次Convolution和Max Pooling,第一次Convolution的参数是9个,因为Filter是3*3的,一个Filter,第二次参数就是225个,因为每一个Filter是3*3,但是高是25的,所以参数就是3*3*25
然后将得到的50 x 5 x 5的image经过Flatten,再经过一个全连接网络,就是CNN的全过程