开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 时序分析 40 - 时序预测从ARIMA到SARIMAX(九)超参调优与最佳模型 -> 正文阅读

[人工智能]时序分析 40 - 时序预测从ARIMA到SARIMAX(九)超参调优与最佳模型

时序分析 40

从ARIMA到SARIMAX(九)超参调优与最佳模型

接上…

超参调优

我们是否有方法使模型表现得更好呢？
可以使用网格搜索来进行超参数调优，下面我们将针对changepoint_prior_scale 和 seasonality_prior_scale进行参数搜索。前者决定了趋势的灵活性，也就是在趋势改变点上趋势变化多少，而后者控制了季节性的弹性。

import itertools

param_grid = {  
    'changepoint_prior_scale': [0.001, 0.01, 0.1, 0.5],
    'seasonality_prior_scale': [0.01, 0.1, 1.0, 10.0],   
}

# Generate all combinations of parameters
all_params = [dict(zip(param_grid.keys(), v)) for v in itertools.product(*param_grid.values())]
maes = []  # Store the MAE for each params here
mapes = [] # Store the MAPE for each params here

# Use cross validation to evaluate all parameters
for params in all_params:
    m = Prophet(**params).fit(df_store_2_item_28)  # Fit model with given params
    df_cv = cross_validation(m, horizon='90 days')
    df_p = performance_metrics(df_cv, rolling_window=1)
    maes.append(df_p['mae'].values[0])
    mapes.append(df_p['mape'].values[0])

# Find the best parameters
tuning_results = pd.DataFrame(all_params)
tuning_results['mae'] = maes
tuning_results['mape'] = mapes

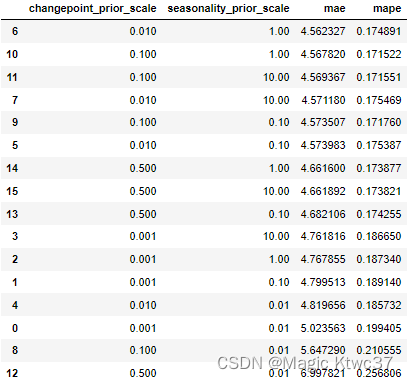
在这里插入图片描述
…

tuning_results_df = pd.DataFrame(tuning_results)
tuning_results_df.sort_values(['mae','mape'])

在这里插入图片描述

tuning_results_df.sort_values(['mape','mae'])

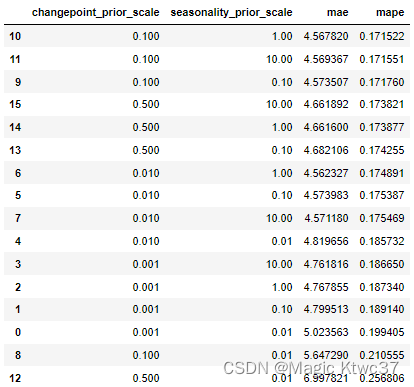
在这里插入图片描述
我们选择产生最小的MAPE的参数。

best_params = all_params[np.argmin(mapes)]
print(best_params)

{‘changepoint_prior_scale’: 0.1, ‘seasonality_prior_scale’: 1.0}

最佳模型

m = Prophet(interval_width=0.95, weekly_seasonality=True, 
            changepoint_prior_scale=best_params['changepoint_prior_scale'], 
            seasonality_prior_scale=best_params['seasonality_prior_scale'])
model = m.fit(df_store_2_item_28)

future = m.make_future_dataframe(periods=90) #to predict 90 days in the future
forecast = m.predict(future)

df_merge = pd.merge(df_store_2_item_28, forecast[['ds','yhat_lower','yhat_upper','yhat']],on='ds')
df_merge = df_merge[['ds','yhat_lower','yhat_upper','yhat','y']]

# calculate MAE between expected and predicted values for december
y_true = df_merge['y'].values
y_pred = df_merge['yhat'].values
mae_02 = mean_absolute_error(y_true, y_pred)
print('MAE: %.3f' % mae_02)

MAE: 4.270

mape_02 = mean_absolute_percentage_error(y_true, y_pred)
print('MAPE: %.3f' % mape_02)

MAPE: 0.168

似乎经过超参调优的模型和第一个模型并没有什么明显的差别。

df_cv = cross_validation(m, horizon='90 days')
# df_cv = cross_validation(m, initial='270 days', period='45 days', horizon = '90 days')

df_p = performance_metrics(df_cv)
df_p.head()

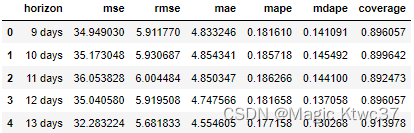
在这里插入图片描述
仔细比较一下，

metrics_prophet_01 = [round(mae_01,3), 
                 round(mape_01,3)]

metrics_prophet_02 = [round(mae_02,3), 
                 round(mape_02,3)]

pd.DataFrame({'metrics':['MAE','MAPE'],
              'Prophet_01':metrics_prophet_01, 
              'Prophet_02':metrics_prophet_02,
             })

在这里插入图片描述
经过调参的模型比第一个模型有非常小的提高。

最佳模型+节假日

看看如果我们加上节假日这个因素是否可以提高模型的性能，这有些类似于上篇文章中的SARIMAX。

m = Prophet(interval_width=0.95, weekly_seasonality=True, 
            changepoint_prior_scale=best_params['changepoint_prior_scale'], 
            seasonality_prior_scale=best_params['seasonality_prior_scale'])
m.add_country_holidays(country_name='US')
model = m.fit(df_store_2_item_28)

future = m.make_future_dataframe(periods=90) #to predict 90 days in the future
forecast = m.predict(future)

df_merge = pd.merge(df_store_2_item_28, forecast[['ds','yhat_lower','yhat_upper','yhat']],on='ds')
df_merge = df_merge[['ds','yhat_lower','yhat_upper','yhat','y']]

# calculate MAE between expected and predicted values for december
y_true = df_merge['y'].values
y_pred = df_merge['yhat'].values
mae_03 = mean_absolute_error(y_true, y_pred)
print('MAE: %.3f' % mae_03)

MAE: 4.269

mape_03 = mean_absolute_percentage_error(y_true, y_pred)
print('MAPE: %.3f' % mape_03)

MAPE: 0.168

df_cv = cross_validation(m, horizon='90 days')
# df_cv = cross_validation(m, initial='270 days', period='45 days', horizon = '90 days')

metrics_prophet_03 = [round(mae_03,3), 
                 round(mape_03,3)]

pd.DataFrame({'metrics':['MAE','MAPE'],
              'Prophet_01':metrics_prophet_01, 
              'Prophet_02':metrics_prophet_02,
              'Prophet_03':metrics_prophet_03,
             })

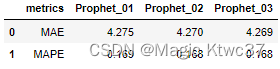
在这里插入图片描述
考虑节假日后，又有了一点点提高。

df_p = performance_metrics(df_cv)
df_p.head()

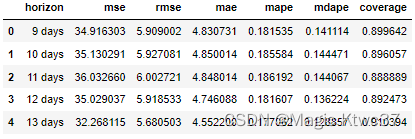
在这里插入图片描述

比较所有模型

prophet_results = pd.DataFrame({'metrics':['MAE','MAPE'],
              'Prophet_01':metrics_prophet_01, 
              'Prophet_02':metrics_prophet_02,
              'Prophet_03':metrics_prophet_03,
             })

# merge by columns metrics
df_arima_results.merge(prophet_results, on='metrics')

在这里插入图片描述

总结

很明显，Prophet的模型的性能指标明显要优于SARIMA模型，这是不是归功于对季节因素的加性建模呢？这个问题留给读者吧。

在这个实践案例中，我们的模型经历了从ARIMA->SARIMA->SARIMAX->Prophet，我们也用了可视化、探索式数据分析、假设检验、参数调优、模型评估等多种工具。但笔者认为实际上这些都不是最重要的，本质问题是每一个模型解决问题的出发点是什么，它的底层逻辑是什么，更好的模型为什么会好，它多考虑了什么因素，多捕获了什么特征和信息。这些问题才是真正值得思考的。其实我们也可以用长短期记忆网络来再对这个案例进行建模，结果可能比Prophet模型又稍微提高一点，但这种提高的意义就不大了。如果复杂的神经网络模型不能显著性的提高模型指标，那么相比之下它必然不会被选择，因为其代价高昂且不可解释。笔者一向不认为神经网络模型是一种革命性的进步，它只不过是由于数据获取的成本降低、算力成本降低的产物（当然还有其他原因、这里不便提及)。笔者还是希望读者更深层次地思考本质问题，也非常欢迎大家和我交流。感谢大家。