SEIR模型是现在较为成熟流行病预测模型,所研究的传染病具有一定时间的潜伏期,与患者接触的正常人并不会马上患病,而是成为病原体的携带者,相比传统的SIR模型更符合新冠疫情的传播规律。传统的SEIR模型包含四大部分,即易感染者、潜伏者、患病者、康复者。本文将上海疫情统计数据与SEIR模型一一对应,通过添加自我隔离者,医疗隔离者等部分,使得改进的SEIR模型更加符合COVID-19疫情的传播规律。通过改进传统的SEIR模型,使得使得模型更加完备准确。并应用实际上海疫情数据来拟合,从而来预测上海疫情的后续发展。模型的预测结果显示感染率峰值大致在0.1%,易感人群占比最低为99%,均与实际情况相符合,显示出模型预测的准确性。
问题描述
考察地区的总人数 N 不变,即不考虑生死或迁移;
传统的SEIR人群分为易感者(S 类)、暴露者(E 类)、患病者(I 类)和康复者(R 类)四类;
易感者(S 类)与患病者(I 类)有效接触即变为暴露者(E 类),暴露者(E 类)经过平均潜伏期后成为患病者(I 类);患病者(I 类)可被治愈,治愈后变为康复者(R 类);康复者(R类)获得终身免疫不再易感;
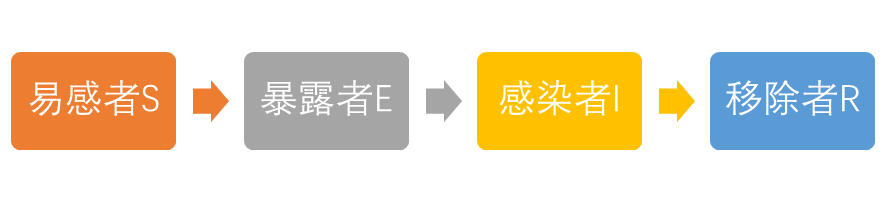
将第 t 天时 S 类、E 类、I 类、R 类人群的占比记为 s(t)、e(t)、i(t)、r(t),数量分别为 S(t)、E(t)、I(t)、R(t);初始日期 t=0 时,各类人群占比的初值为 s0、e0、i0、r0;
日接触数 λ,每个患病者每天有效接触的易感者的平均人数;
日发病率 δ,每天发病成为患病者的暴露者占暴露者总数的比例;
日治愈率 μ,每天被治愈的患病者人数占患病者总数的比例,即平均治愈天数为 1/μ;
传染期接触数 σ=λ/μ,即每个患病者在整个传染期内有效接触的易感者人数。
SEIR模型的微分方程模型
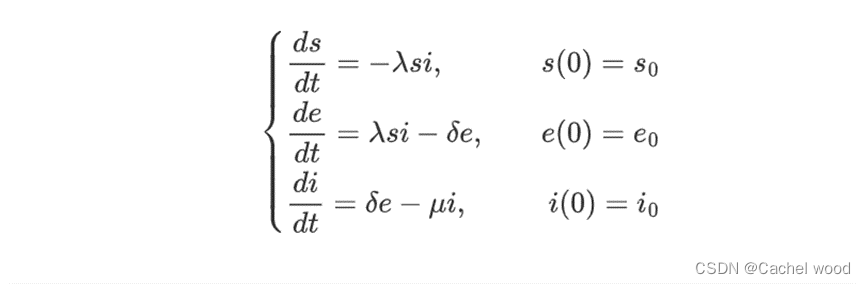
模型分析与求解
- 经典SEIR模型分析
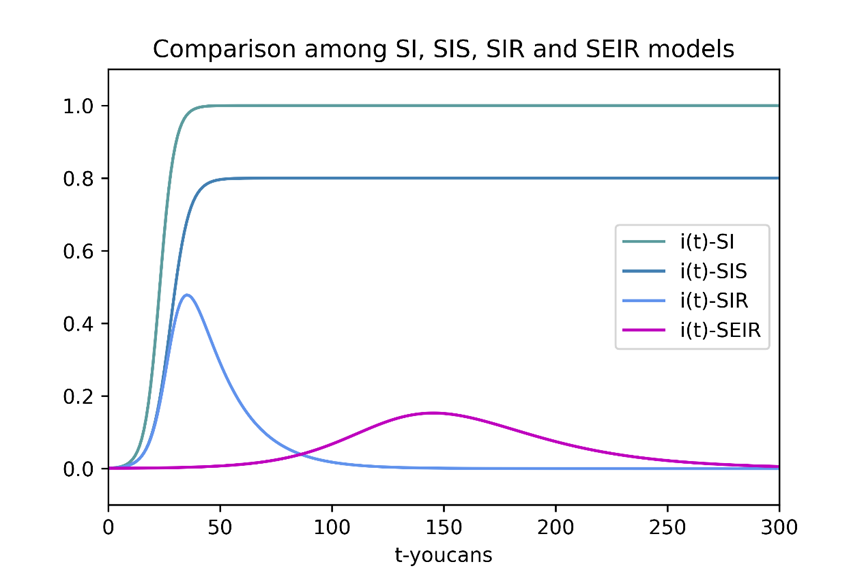
上图对应的参数初值为:λ=0.3,δ=0.03,μ=0.06,(s0,e0,i0)=(0.001,0.001,0.998),上图为例程的运行结果。
曲线 i(t)-SI 是 SI 模型的结果,患病者比例急剧增长到 1.0,所有人都被传染而变成患病者,不符合实际。
曲线 i(t)-SIS 是 SIS 模型的结果,患病者比例快速增长并收敛到某个常数,即稳态特征值 i_\infty=1-\mu/\lambda=0.8,表明疫情稳定,并将长期保持一定的患病率。
曲线 i(t)-SIR 是 SIR 模型的结果,患病者比例 i(t) 先上升达到峰值,然后再逐渐减小趋近于常数。SIR模型一定程度上可以反映传染病的传播情况,但是对于有一定潜伏期的传染病,增加作为潜伏期的E阶段更加贴合实际情况。
曲线i(t)-SEIR是SEIR模型的结果,曲线与SIR模型的i(t) 曲线类似,上升达到峰值后逐渐减小,最终趋于 0;但患病者比例曲线发展、达峰的时间比潜伏者曲线要晚一些,峰值强度也较低。
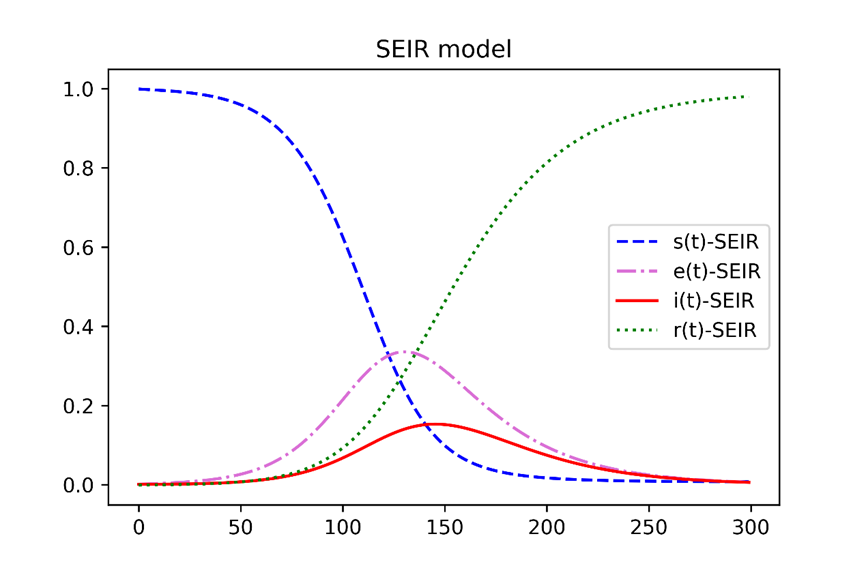
单独考察SEIR模型的四条曲线,感染率曲线和暴露率曲线基本上同步,暴露率曲线高于感染率曲线,都呈现先逐步达到峰值并逐渐回落的趋势。易感人群的占比不断降低直到下降为0,移除者(治愈者和死亡者)的占比逐步上升。总体来看i(t)和e(t)符合一般规律,但是实际新冠疫情的实际传播过程中,绝大多数人群并不会经过治愈变为移除者,而是一直处于易感者人群,因为政府的强力控制和居民的自我隔离,大多数易感者可以隔离于整个系统之外,这是建模时候需要考虑的情况。
2. 收集上海疫情数据并分析
在上海市卫健委官网公布的每日疫情情况公告中,记录每日有关疫情的关键数据信息,具体包括新增确诊、新增无症状感染者、新增治愈、新增死亡、解除隔离者、无症状转确诊病例、当前在院就诊病例以及累计确诊、累计治愈等最为全面的疫情数据信息,需要耗费比较多的时间进行统计。由于公布信息口径的变化以及统计形式的变化,个别数据有缺失。
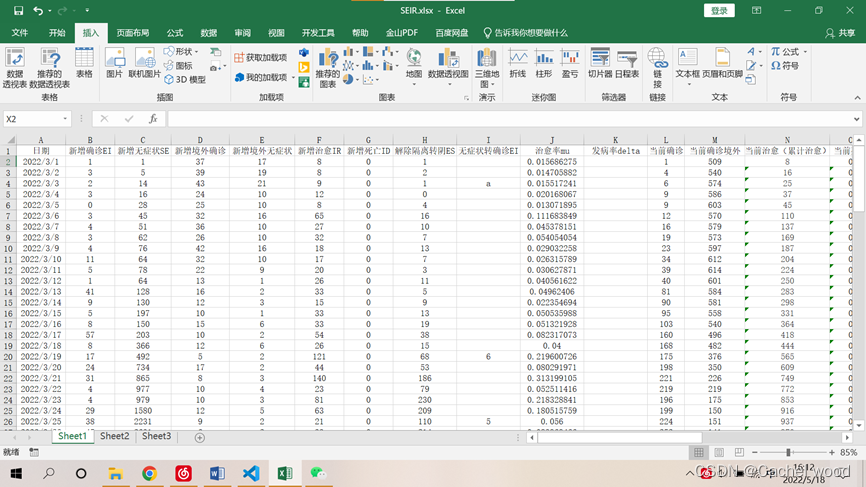
收集数据之后进行统计分析,绘制可视化图表来观察数据走势。
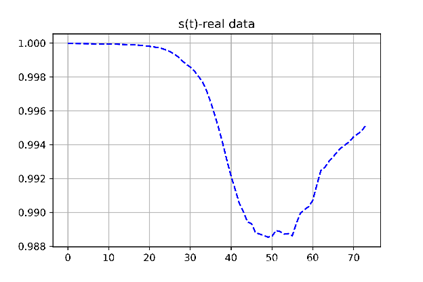
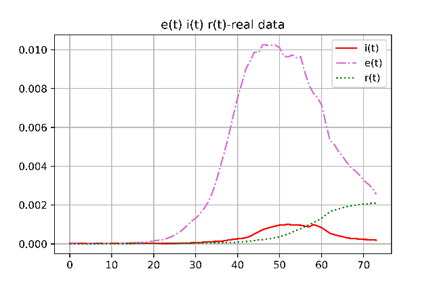
可以看出从3月1日到现在各个曲线的走势,我们的目标是尽可能使得改进的模型接近真实情况。
新冠疫情属于有潜伏期的传染病,潜伏期一般在2-14天,也有可能更长,所以采用SEIR模型更为合适,但是传统的SEIR模型认为在exposed(暴露者)阶段没有传染性,而且只会过渡到下一个阶段infected(感染者),但是新冠疫情的无症状感染者也具有传染性,但它的复杂性在于一部分无症状传染者可以通过自愈转为阴性,重新进入易感人群(susceptible),所以不同于传统的SEIR模型。
除了自我隔离之外,迅速的流调结果和对密切接触人群的控制使得传染病的有效传染人数大幅度降低,但是严格的全市封控措施实施之前和实施之后市民的流动率仍有很大变化,所以考虑严格封控前后的参数变化对于模型仍有重要意义。上海市从3月28日开始对浦东全面封控,4月1日开始全程封控,我们取28天为两种政策分界点。参考以上思考,提出改进SEIR的新模型。
3. 改进的SEIR模型
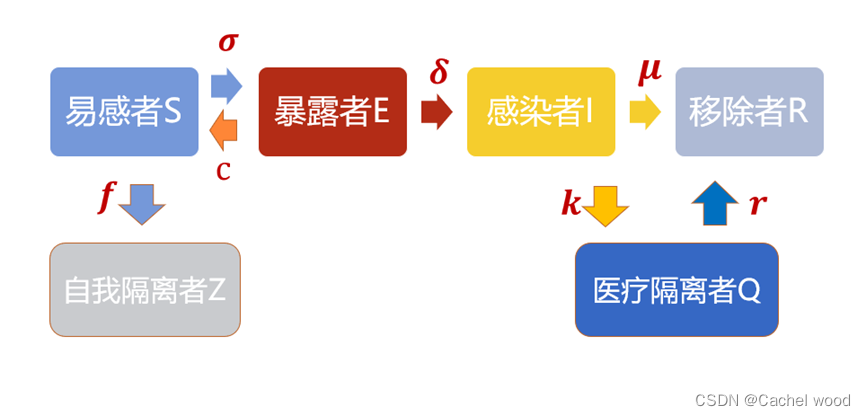
- 参数解释
| 参数 | 含义 |
|---|---|
| s | 易感者占比 |
| e | 暴露者占比 |
| i | 感染者占比 |
| z | 自我隔离者占比 |
| q | 医疗隔离者占比 |
| λ \lambda λ | 日有效接触易感者数目 |
| δ \delta δ | 日发病率 |
| μ \mu μ | 日治愈率 |
| c | 暴露者自愈率 |
| f | 日自我隔离速率 |
| k | 日医疗隔离速率 |
| r | 医疗隔离者移除率 |
| t m a r k t_{mark} tmark? | 3月1日至开始严格封控的天数 |
-
问题建模
对问题进行微分方程建模。
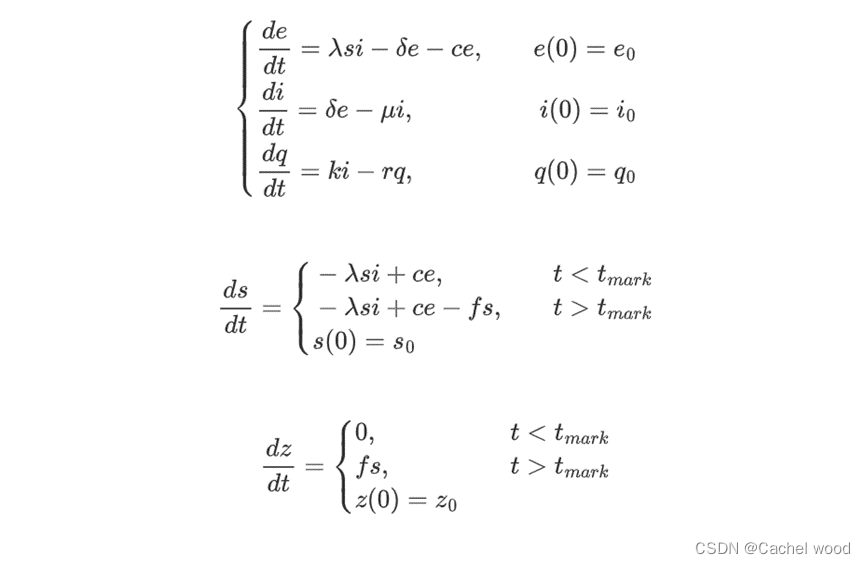
-
编程计算及可视化
利用python进行建模求解及可视化,经过确定不同参数范围并且细致调整参数之后,基本确定拟合比较好的参数,并且绘制不同人群在两个多月时间内的趋势轨迹,寻找规律。
lamda=2,delta=0.15,mu=0.3,tEnd=78,i0=2e-5,e0=2e-5,q0=0,z0= 5e-2,c = 0.3,f = 0.3, k=0.3, r=0.2,t_mark = 28
结果解释、讨论与管理决策建议
- 结果解释
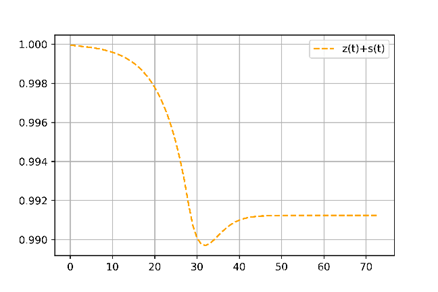
对比实际曲线和我们的预测曲线,我们把自我隔离者和剩余的易感者与实际的易感者相对应,在易感者的预测上与实际曲线趋势一致,并且最低点都在99%,十分相符,不足之处在于实际曲线大致在本轮疫情开始50天后易感者达到最低点,我们的模型在30多天便达到最低点。
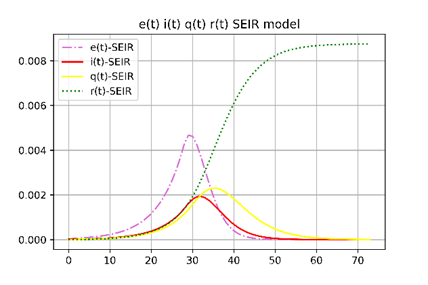
对比更加能够反映真实情况的感染率曲线、暴露率曲线,模型能够很好地表示两条曲线的同趋势状况,也即同时达到峰值,我们预测感染者最高可达接近0.2%,暴露者可达0.5%,实际情况是感染者占比0.1%,暴露者占比1%,两者最高差距十倍。这一方面是我们的参数还需要继续调整,另一方面是模型难以完全表示真实的疫情状态,无法完全表达出影响疫情的因素,另外采集的数据是否可以完全表示实际的疫情走势也值得讨论。
移除率曲线最终趋向于0.85%,在不引入自我隔离者之前,传染病将不断蔓延直至所有人都变为移除者,而当引入自我隔离者之后移除率基本上符合实际情况,相比实际情况略高。
总体来看,通过改进SEIR模型,加入自我隔离者和医疗隔离者,提出新冠病毒的暴露者具有自愈的状况而引入自愈率之后,模型更加可以反映实际情况。在总体趋势上与实际疫情数据发展完全吻合,各部分的比例预测上相对比较好,尤其是对于感染者和易感者的预测基本吻合,这对于未来疫情发展判断具有重要意义,但是对于拐点的预测与实际情况有所偏离。另外由于固定参数,所以可能不能更加灵敏地反映实际疫情的发展。 - 灵敏性分析
(1).tmark变化
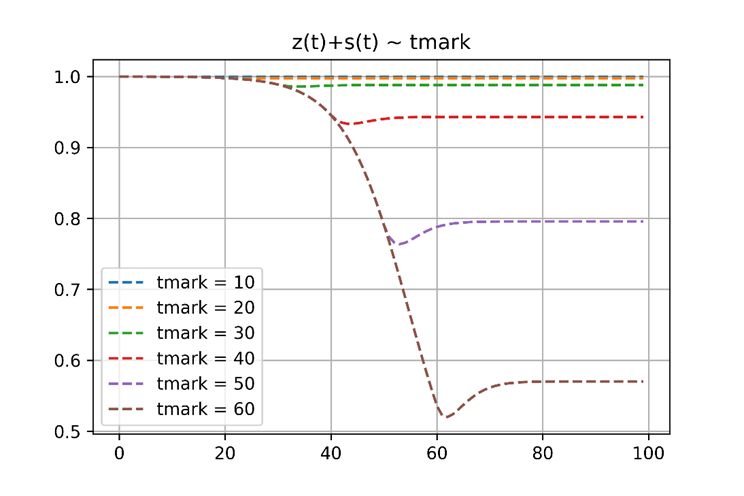
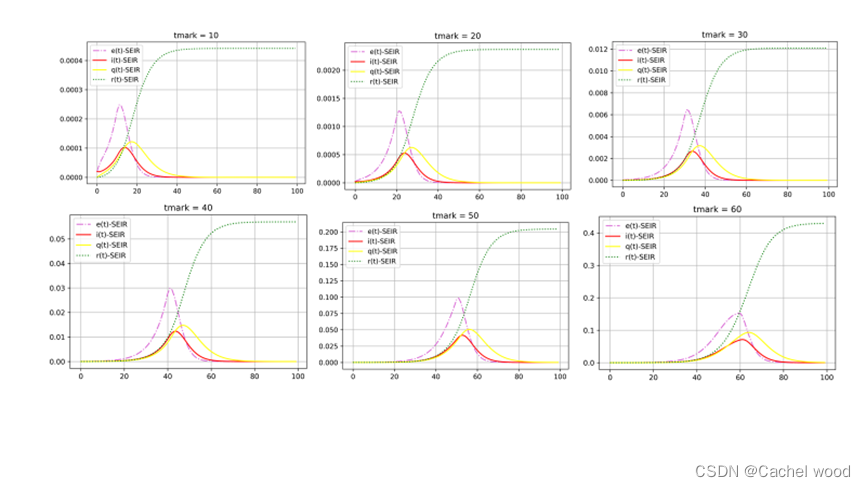
严格封控开始时间对于疫情发展的意义重大,从灵敏性分析结果可以看出,疫情开始10天到20天开始封控,因为病毒还没有大规模扩散,基本可以完全抑制;30天开始封控,此时对于特大型城市来说感染基数已经相当庞大,正是此次上海疫情发生的状况,医疗挤兑严重,但是还在可控范围之内,如果严格封控再晚10天达到40天之后再严格封控,将有数十万人甚至百万人感染,那时问题将极具严重。本次疫情发生迅猛,严格封控需要考虑社会成本和市民等因素,需要慎重考虑。
(2)日自我隔离速率f
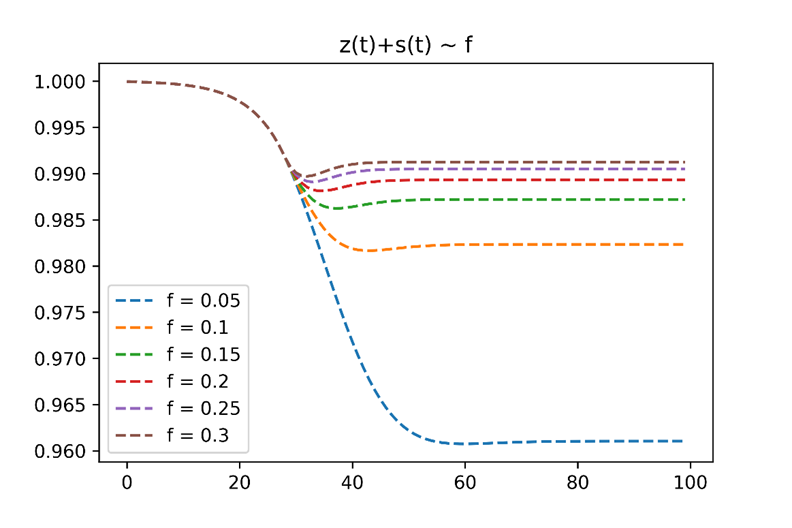
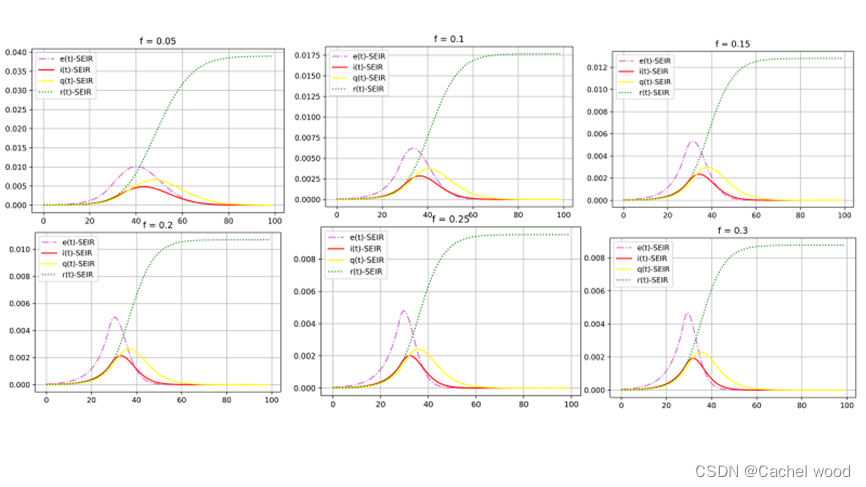
自我隔离速率越高,遭遇新冠病毒的可能性更低,当f>0.2时免受新冠病毒的人群比例可达99%。通过强有力的基层动员完全可以达到这样的隔离速率,因此自我隔离是预防新冠病毒的实用手段。
(3)日发病率
δ
\delta
δ
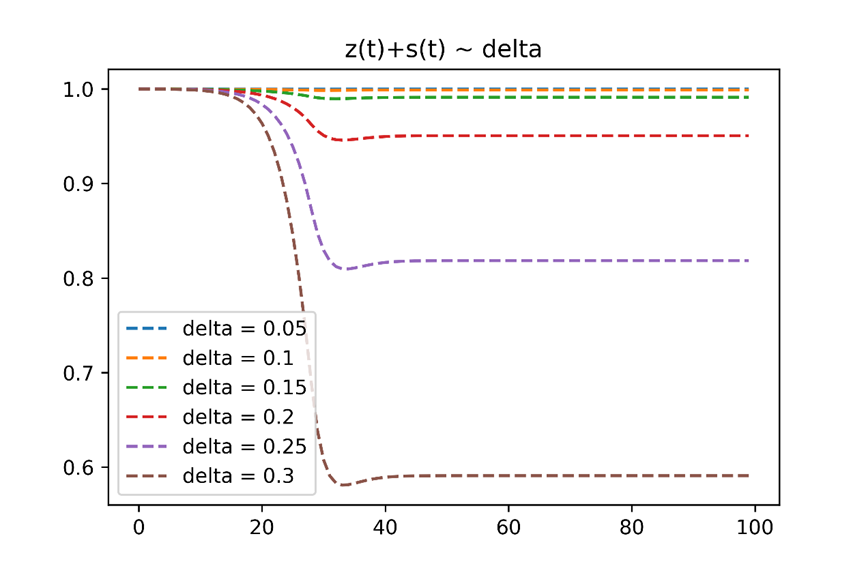
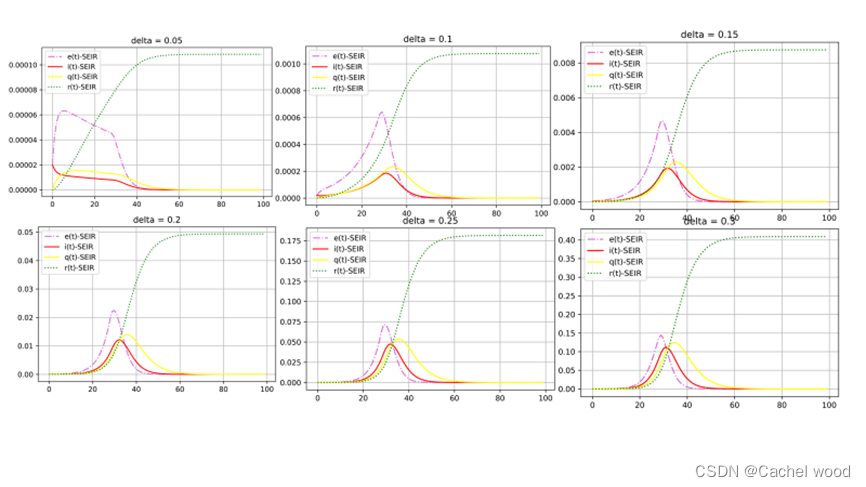
日发病率主要取决于病毒的特点和管控措施等,发病率控制在0.15一下基本上再可控范围之内,当发病率大于0.15之后会迅速感染大量人群,导致疫情的不可控。
- 管理决策建议
通过以上分析,得到以下的政策建议:
- 政府工作人员需要迅速使得确诊病例、无症状感染者和密切接触者处于隔离状态,使得病毒有效传染人数大大降低;
- 疫情爆发阶段,政府需要迅速动员广大市民自我隔离,使得社会上的易感人群处于自我隔离状态,降低实际上存在的易感人群,实际上还是减少有效易感人数;
- 政府需要及时研判疫情势头,当疫情形势逐渐严峻时,必须在严格封控带来的社会成本和疫情蔓延之间迅速做出判断,果断选择极其严格的封控措施,一旦错过最佳封控时间导致疫情蔓延,疫情将走向不可控。当然,必须重视随之而来的配套措施。
附录
- 绘制改进SEIR模型代码
import pandas as pd
import matplotlib.colors as mcolors
colors=list(mcolors.TABLEAU_COLORS.keys()) #颜色变化
def dySEIR(y, t, lamda, delta, mu, c, f, k, r, tmark): # SEIR 模型,导数函数
s, e, i, q, z = y # youcans
if t<tmark:
ds_dt = -lamda*s*i + c*e
dz_dt = 0
else:
dz_dt = f*s
ds_dt = -lamda*s*i + c*e - f*s # ds/dt = -lamda*s*i
de_dt = lamda*s*i - delta*e - c*e # de/dt = lamda*s*i - delta*e
di_dt = delta*e - mu*i # di/dt = delta*e - mu*i
dq_dt = k*i - r*q
return np.array([ds_dt,de_dt,di_dt,dq_dt,dz_dt])
def plotseir(number=1e5,lamda=2,delta=0.15,mu=0.3,tEnd=100,i0=2e-5,e0=2e-5,q0=0,z0= 5e-2,c = 0.3,f = 0.3, k=0.3, r=0.2, tmark=28):
t = np.arange(0.0,tEnd,1) # (start,stop,step)
s0 = 1-i0-e0-q0-z0 # 易感者比例的初值
sigma = lamda / mu # 传染期接触数
fsig = 1-1/sigma
Y0 = (s0, e0, i0, q0, z0) # 微分方程组的初值
colors=list(mcolors.TABLEAU_COLORS.keys()) #颜色变化
for i in range(5,33,5):
delta = i/100
ySEIR = odeint(dySEIR, Y0, t, args=(lamda,delta,mu,c,f,k,r,tmark)) # SEIR 模型
print("lamda={}\tdelta={}\tmu={}\tc={}\tf={}\tk={}\tr={}\ttmark={}".format(lamda,delta,mu,c,f,k,r,tmark))
plt.grid()
#plt.plot(t, ySEIR[:,0], '--', color='blue', label='s(t)-SEIR')
plt.plot(t, ySEIR[:,1], '-.', color='orchid', label='e(t)-SEIR')
plt.plot(t, ySEIR[:,2], '-', color='red', label='i(t)-SEIR')
plt.plot(t, ySEIR[:,3], '-', color='yellow', label='q(t)-SEIR')
plt.plot(t, 1-ySEIR[:,0]-ySEIR[:,1]-ySEIR[:,2]-ySEIR[:,3]-ySEIR[:,4], ':', color='green', label='r(t)-SEIR')
#plt.text(0.02,0.36,f"tmark = {tmark}",color='black')
plt.legend(loc='best') # youcans
plt.title(f'delta = {delta}')
plt.savefig(f'eiqr-delta = {delta}.png',dpi=600)
plt.show()
for i in range(5,33,5):
delta = i/100
j = i/5-1
plt.grid()
# odeint 数值解,求解微分方程初值问题
ySEIR = odeint(dySEIR, Y0, t, args=(lamda,delta,mu,c,f,k,r,tmark)) # SEIR 模型
print("lamda={}\tdelta={}\tmu={}\tc={}\tf={}\tk={}\tr={}\ttmark={}\t".format(lamda,delta,mu,c,f,k,r,tmark))
#plt.plot(t, ySEIR[:,4], '-', color='pink', label='z(t)-SEIR')
#plt.plot(t, ySEIR[:,0], '--', color='blue', label='s(t)-SEIR')
plt.plot(t,ySEIR[:,0]+ySEIR[:,4],'--',label = f'delta = {delta}')
plt.legend()
plt.title('z(t)+s(t) ~ delta')
plt.savefig(f'delta = {delta}.png',dpi=600)
plt.show()
plotseir()
- 绘制实际数据曲线代码
df = pd.read_excel('SEIR.xlsx')
plt.grid()
#plt.subplot(211)
plt.plot(df.iloc[:,-4], '--', color='blue', label=df.columns[-4])
plt.title('s(t)-real data')
plt.savefig('s(t).png',dpi=600)
plt.show()
#plt.subplot(212)
plt.grid()
plt.plot(df.iloc[:,-2], '-', color='red', label=df.columns[-2])
plt.plot(df.iloc[:,-3], '-.', color='orchid', label=df.columns[-3])
plt.plot(df.iloc[:,-1],':', color='green', label=df.columns[-1])
plt.legend()
plt.title('e(t) i(t) r(t)-real data')
plt.savefig('real.png',dpi=600)
