[人工智能]关于SIoU《SIoU Loss: More Powerful Learning for Bounding Box Regression Zhora Gevorgyan 》的一些看法

最近很多公众号都在推这篇文章，但是我在阅读的过程中产生了一些问题，由于代码未开源，理解可能不正确，因此先记录一下，等开源之后对照代码再更深地去理解，也希望如果有大佬看见这篇文章的时候，能对我不成熟的看法给予一些意见。
文章实验的最终损失函数计算如下：

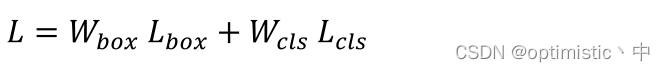
其中$L_{cls}$是用了focal loss，$W_{box}$和$W_{cls}$权重参数是根据遗传算法计算得来的，$L_{box}$是本文所提的SIoU损失，计算如下：

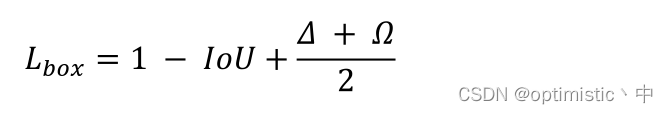
主要是涉及到四部分损失：角度损失 、距离损失 、形状损失 、IoU 损失
1.角度损失

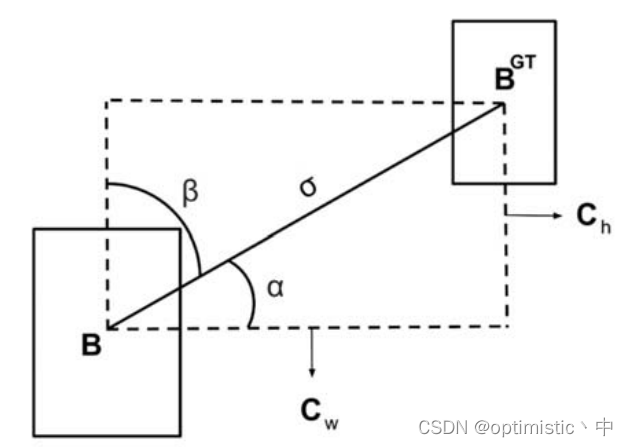
这里作者认为，可以考虑角度因素，首先使得预测框回归到与真值框同一水平线或者垂直线上，这点我很认同，可以加速收敛，作者是通过以下公式评估损失的

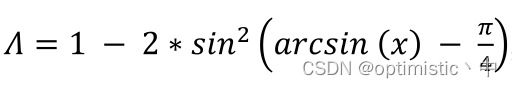
该公式由两部分组成，第一部分是$1?2si{n}^2(x)$，其实也就是$cos(2x)$，使得对于$x>0$的情况，其值只有在$x$为$\pi /4$的时候取最小，得到0，而在$x$为0的时候取最大，得到1；第二部分是$arcsin(x)?\pi /4$，其中$arcsin(x)$也就是$\alpha$，还需要进行$?\pi /4$的操作是需要考虑到让预测框朝角度较小的一边进行移动，因为$\beta$等于$\pi /2?\alpha$，两者$?\pi /4$后互为相反数，经过$cos$函数计算后的值是一样的，当$\alpha$为0的时候，其损失最小，而为$\pi /4$的时候最大。最终使得预测框更快地移动到真值框所在的水平线或者垂直线上。
2.距离损失

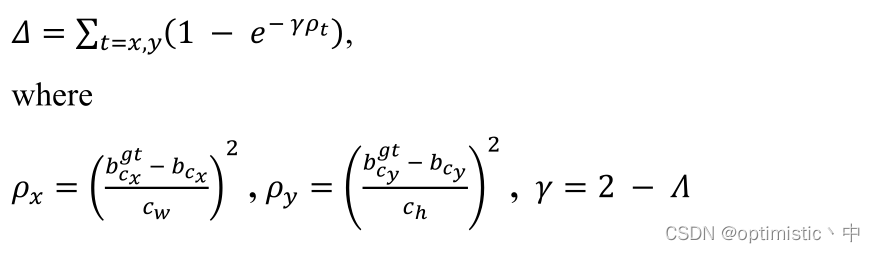
（1）对于${\rho }_x$和${\rho }_y$的计算，如果我对公式没理解错的话，其计算结果永远是1，好像无法反映距离，而且文章也说明了 $c_h$的计算方式，更佐证了我的看法，因此猜测这里是作者写错了或者是我理解错了。

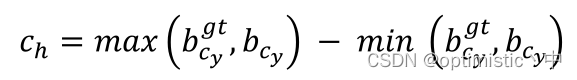
（2）对于$\gamma$的计算方式，我的理解是首先由角度损失计算可以得到$\Lambda$的范围应该是[0,1]，这里再经过$2?\Lambda$，首先防止$\gamma$为0时${\rho }_t$失效的情况，其次使得$\Lambda$越小，${\rho }_t$变化对于损失的影响就越大。
（3）对于$（1?e^{?\gamma {\rho }_t}）$的计算方式，我的理解是，假如对于${\rho }_t$这里的计算方式是作者写错了，而且与距离正相关的话，那么这里的目的是使距离越大损失越大但又不会超过1，防止梯度爆炸。
3.形状损失

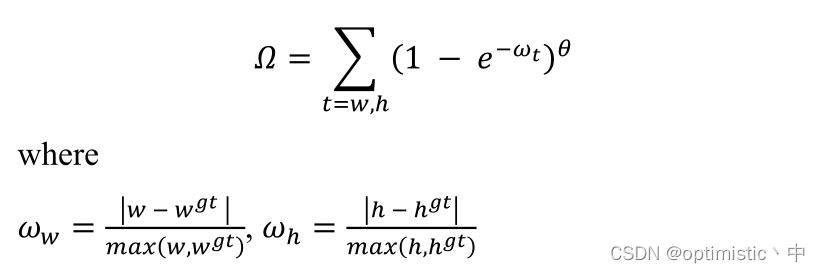
这里和EIOU一样，都考虑到了预测框和真值框之间的真实长宽比，不过对于${\omega }_x$和${\omega }_y$的计算，与EIOU中还需要计算能包围两个框的最小框长宽不一样，这里只用到了真值框和预测框的长宽属性，计算量更少，按理会更快，但是具体效果还不清楚。另外，${\omega }_t$的范围是[0,1]，我认为应该不需要通过$1?e^{?{\omega }_t}$进一步计算，说不定效果会更好，最后对于 $\theta$的引入，这里不是很理解。
（1）首先是不理解为什么引入这个因子会更好。
（2）其次距离损失也是可以引入因子的，为什么不引入。
4.IoU损失
和GIOU里提的一样，这里是按$1?IoU$计算得到
对于文章中的一些权重和$\theta$参数都是通过遗传算法对数据集计算得来，不清楚这一部分的提升效果，由于代码未开源，对其中的一些计算方式也存在质疑，因此无法验证每一个改进点真实的效果

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系