GPU与cuda技术协调
深度学习大多进行图像数据的处理和计算,但处理器的CPU大多需要处理,因此无法满足图像处理和计算速度的要求。 显卡GPU是来帮助CPU解决这个问题的。 GPU特别擅长处理图像数据,CUDA (计算机统一设备体系结构)是显卡制造商CUDA是NVIDIA推出的通用并行计算体系结构,GPU复杂, 包括CUDA指令集体系结构(ISA )和GPU内部的并行计算引擎,通过安装CUDA可以加速GPU的运算和处理。
参考文献链接
https://www.zhangshilong.cn/work/35703.html
https://mp.weixin.qq.com/s/7lSuTnoi3V-8-BMP8m53tg
Matrix Multiplication CUDA——https://ecatue.gitlab.io/gpu2018/pages/Cookbook/matrix_multiplication_cuda.html
https://mp.weixin.qq.com/s/TaewNgRtValtFEPQafYs-Q
什么是显卡?
显卡(Video card、Graphics card )完全显示接口卡,即显示适配器,是计算机最基本的配置,也是最重要的附件之一。 显卡作为计算机主体的重要组成部分之一,是计算机进行数模信号转换的设备,承担着输出显示图形的作用。 显卡连接到电脑主板上,将电脑的数字信号转换为模拟信号,显示在显示器上。 显卡还具有图像处理能力,可以帮助CPU运行并提高整体运行速度。 对于专业从事图形设计的人来说,显卡是非常重要的。 民用和军用显卡芯片供应商主要包括AMD (超微半导体)和Nvidia ) NVIDIA (NVIDIA )两家公司。 现在的top500计算机包括图形计算核心。 在科学计算中,显卡被称为显示器加速器卡。
什么是显示内存?
也称为帧缓存,用于存储由图形芯片处理或即将提取的渲染数据。 和计算机内存一样,图形内存是用于存储要处理的图形信息的部件。
显卡、显卡驱动程序和CUDA之间的关系
显卡: (GPU ),主流是NVIDIA的GPU。 因为深度学习本身需要大量的计算。 GPU的并行计算能力在这几年中很好地满足了深度学习的需要。 AMD的GPU几乎不支持,所以不用想。 驱动程序:如果没有显卡驱动程序,GPU硬件将无法被识别,并且无法调用计算资源。 但是,在Linux上安装NVIDIA驱动程序特别麻烦,特别是对初学者来说,这是噩梦。 必须阻止第三方显卡驱动程序。 教程如下所示。 CUDA :是显卡制造商NVIDIA推出的只能用于自家GPU的并行计算框架。 只有安装这个框架才能进行复杂的并行计算。 主流深度学习框架也基于CUDA进行了GPU并行加速,几乎无一例外。 另一个叫做cudnn,是针对深卷积神经网络的加速库。 为什么GPU特别擅长处理图像数据?
这是因为图像上的所有像素点都需要被处理,并且所有像素点的处理过程和方法很相似。 GPU类似于一种纯粹的人海战术,使用许多简单的计算单元执行大量的计算任务。 GPU不仅应用于图像处理领域,还应用于科学计算、解密、数值分析、庞大的数据处理(排序、Map-Reduce等)、金融分析等需要大规模并行计算的领域。
英伟达GPU新核弹—Hopper H100
2022年3月NVIDIA GTC大会上,NVIDIA介绍基于全新Hopper架构GPU——H100,是英伟达迄今为止,用于加速人工智能(AI)、高性能计算(HPC)和数据分析等任务的最强GPU芯片。这颗芯片以计算科学先驱Grace Hopper的姓氏命名。
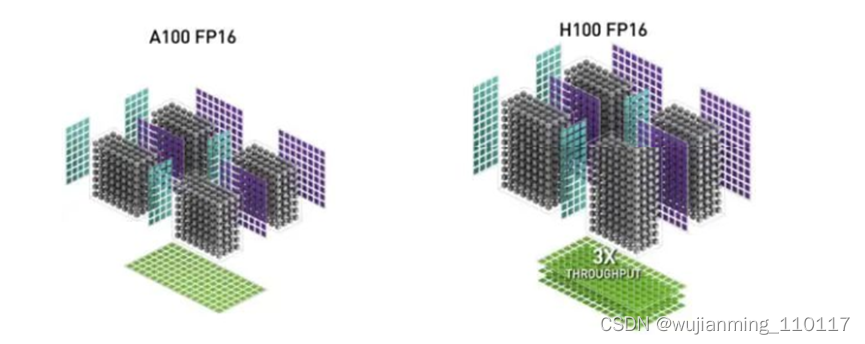
Hopper H100是有史以来最大的代际飞跃。H100具有800亿个晶体管,在性能上堪称NVIDIA的“新核弹”。这颗“新核弹”的核心架构是什么样的?
首先是规格方面,NVIDIA Hopper架构的H100芯片采用台积电4nm工艺(N4是台积电N5工艺的优化版),核心面积为814平方毫米,比A100小14平方毫米。虽然核心面积比A100小14平方毫米,但得益于4nm工艺,晶体管密度数量从542亿提升到800亿。
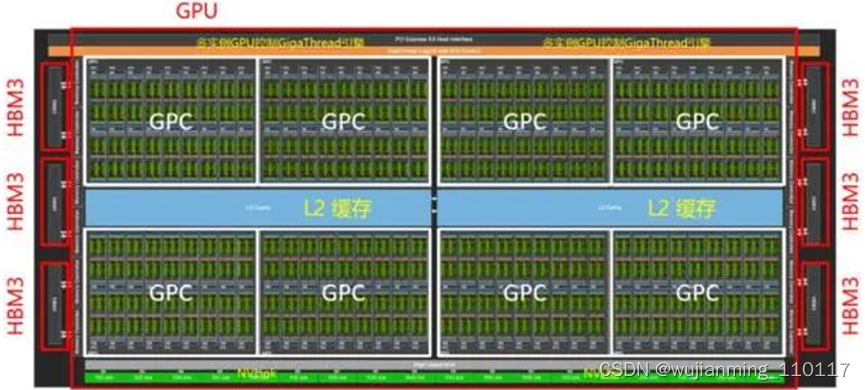
从核心设计图来看,NVIDIA Hopper架构与苹果UltraFusion相似,但它在本质上还是单独的一颗晶片,而不是苹果M1 Ultra那种将两块芯片桥接起来。顶层拓扑与Ampere架构差别不大,整个Hopper架构GPU由8个图形处理集群(Graphics Processing Cluster,GPC)“拼接”组成,但每4个GPC共享25MB得L2缓存。核心两侧则是HBM3显存,拥有5120 Bit的位宽,最高容量可达80GB。
片上的每个GPC由9个纹理处理集群(Texture Processor Cluster,TPC)组成,由PCIe5或接口进入的计算任务,通过带有多实例GPU(Multi-Instance GPU,MIG)控制的GigaThread引擎分配给各个GPC。GPC通过L2缓存共享中间数据,GPC计算的中间数据通过NVLink与其他GPU互通。每个TPC由2个流式多处理器(Streaming Multiprocessor)组成。
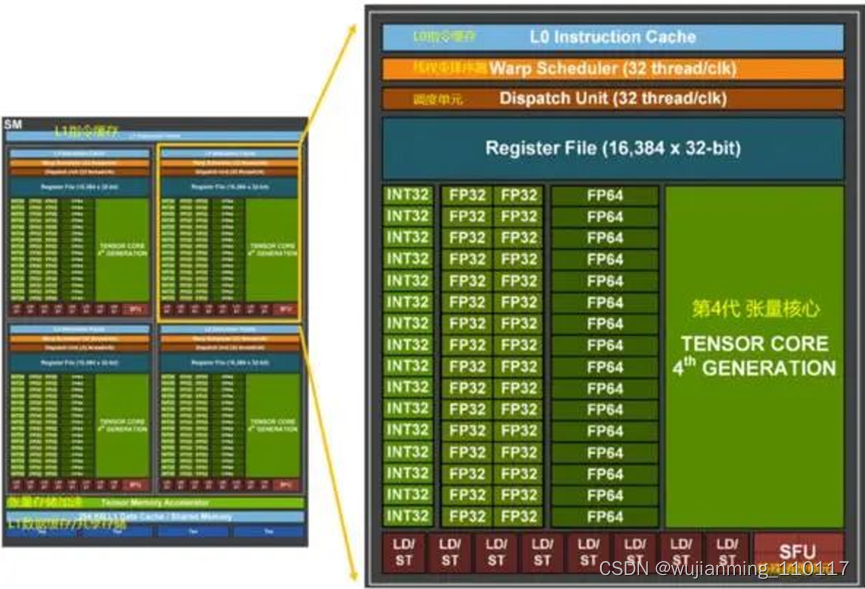
Hopper架构的性能提升和主要变化体现在新型线程块集群技术和新一代的流式多处理器。NVIDIA在Hopper中引入了新的线程块集群机制,可实现跨单元进行协同计算。H100中的线程块集群可在同一GPC内的大量并发运行,对较大的模型具有更好的加速能力。
每个包括128个FP32 CUDA核心、4个第4代张量核心(Tensor Core)。每个单元的指令首先存入L1指令缓存(L1 Instruction Cache),再分发到L0指令缓存(L1 Instruction Cache)。与L0缓存配套的线程束排序器(Wrap Scheduler,线程束)和调度单元(Dispatch Unit)为CUDA核心和张量核心分配计算任务。通过使用4个特殊函数单元(Special Function Unit,SFU)单元,进行超越函数和插值函数计算。
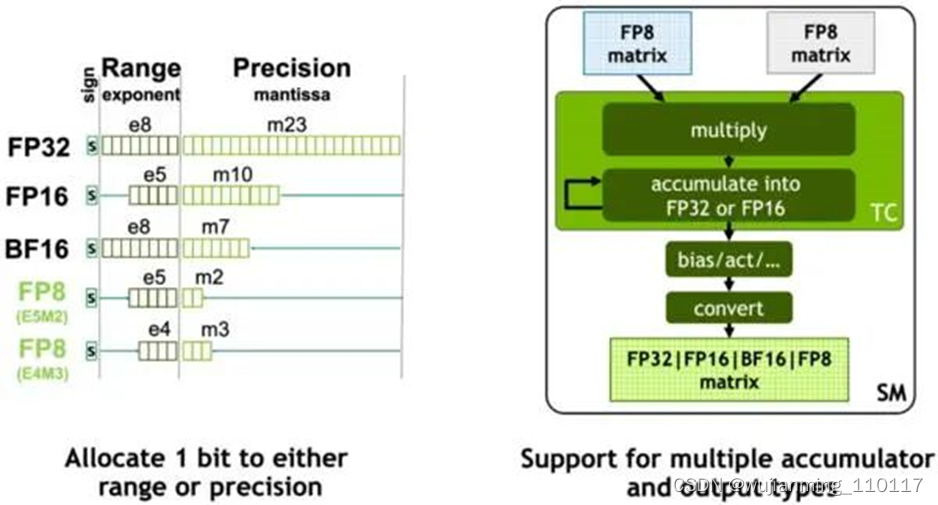
NVIDIA在Hopper架构中引入新一代流式多处理器的FP8张量核心(Tensor Core),用来加速AI训练和推理。FP8张量核心支持FP32和FP16累加器以及两种FP8 输入类型(E4M3和E5M2)。与FP16或BF16相比,FP8将数据存储要求减半,吞吐量翻倍。在Transformer引擎的分析中,还会看到使用FP8可自适应地提升Transformer的计算速度。
在GPU中,张量核心AI加速的关键模块,也是Ampere及之后GPU架构与早期GPU的重要区别。张量核心是用于矩阵乘法和矩阵累加 (Matrix Multiply-Accumulate,MMA) 数学运算的专用高性能计算核心,可为AI和HPC应用程序提供突破性的性能加速。
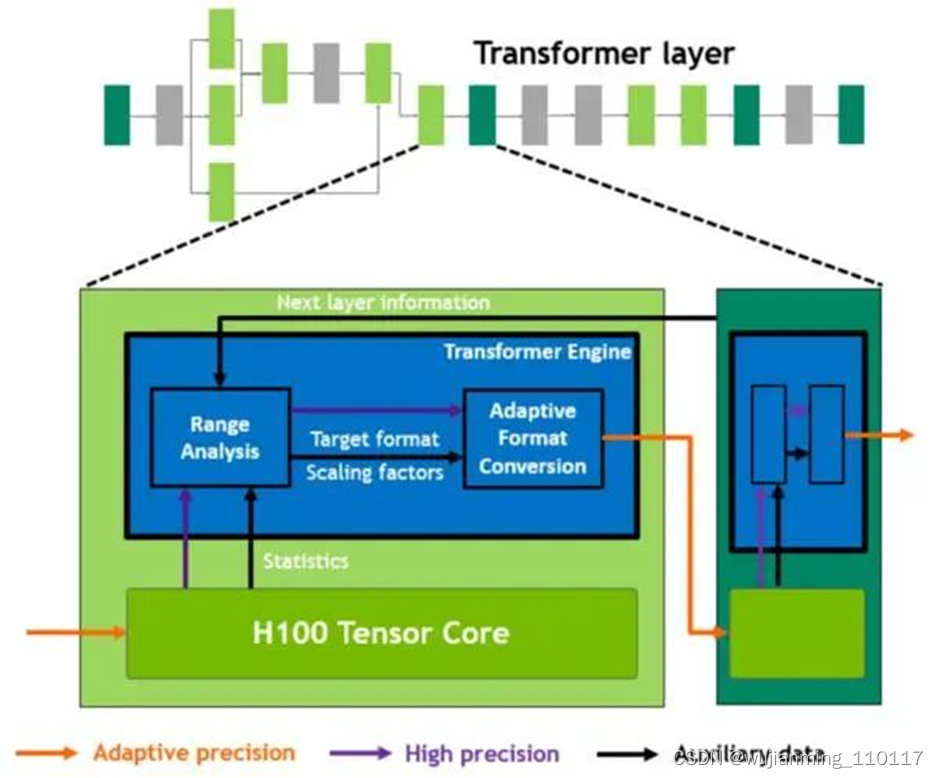
Hopper的张量核心支持FP8、FP16、BF16、TF32、FP64和INT8 MMA数据类型。这一代张量核心的关键点是引入Transformer引擎。Transformer算子是主流的BERT到GPT-3等NLP模型的基础,越来越多地应用于计算机视觉、蛋白质结构预测等不同领域。

与上一代A100相比,新的Transformer引擎与Hopper FP8张量核心相结合,在大型NLP模型上提供高达9倍的AI训练速度和30倍的AI推理速度。为了提升Transformer的计算效率,新Transformer引擎使用混合精度,在计算过程中智能地管理计算精度,在Transformer计算的每一层,根据下一层神经网络层及所需的精度,在FP8和其他浮点格式中进行动态格式转换,充分运用张量核心的算力。
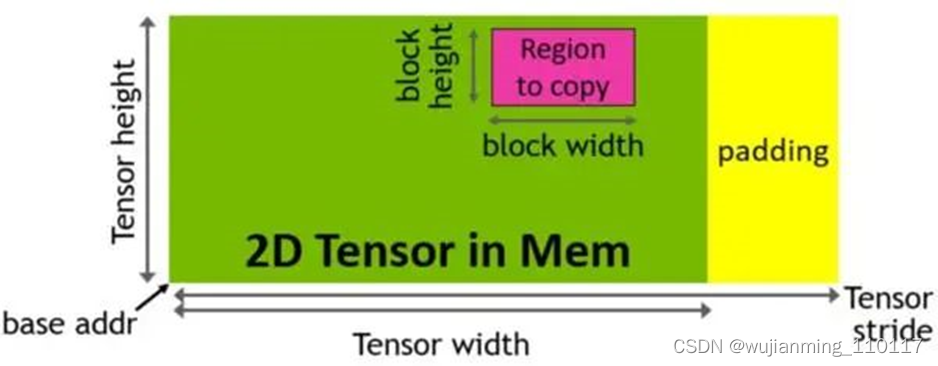
Hopper架构中新增加张量存储加速器 (Tensor Memory Accelerator,TMA) ,以提高张量核心与全局存储和共享存储的数据交换效率。新的TMA使用张量维度和块坐标指定数据传输,而不是简单的按数据地址直接寻址。TMA通过支持不同的张量布局(1D-5D张量)、不同的存储访问模式、显著降低寻址开销并提高了效率。
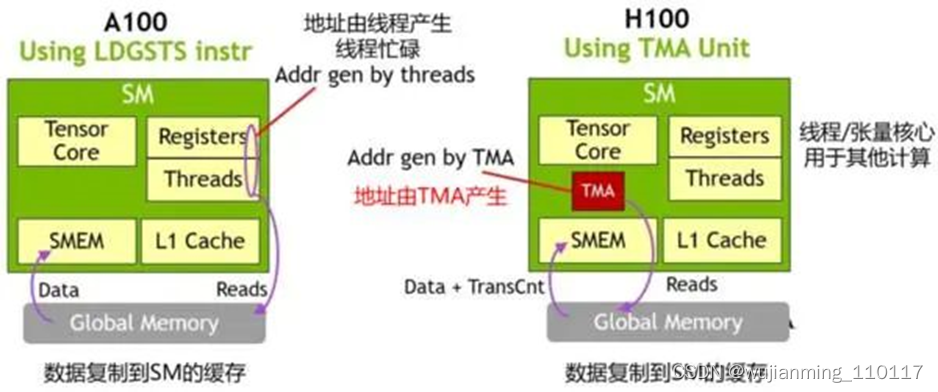
TMA操作是异步的,多个线程可以共享数据通道,排序完成数据传输。TMA的关键优势是可以在进行数据复制的时候,释放线程的算力来执行其他工作。例如,在A100由线程本身负责生成所有地址执行所有数据复制操作;但Hopper中得TMA来负责生成地址序列(这个思路类似DMA控制器),接管数据复制任务,让线程去做其他事。
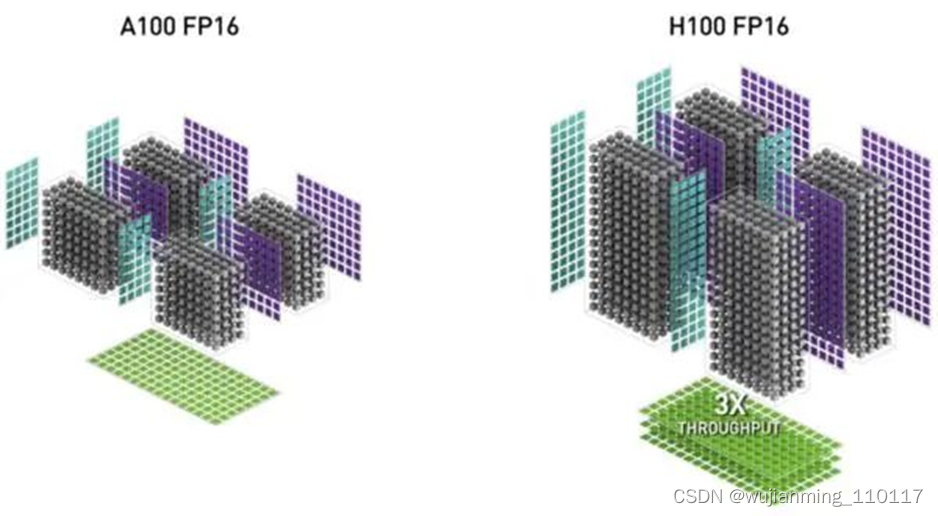
与Ampere A100线相比,基于Hopper架构的H100计算性能提高大约6倍。性能大幅提升的核心原因是NVIDIA引入FP8张量核心和针对NLP任务的Transformer引擎,加上TMA技术减少单元在数据复制时的无用功。
CUDA 并行计算优化策略总结
并行计算为了提高算法运行效率,本文通过以矩阵乘法(C = A * B)的各种实现思路以及优化方法总结为例子,过一遍cuda的几个基础优化策略。
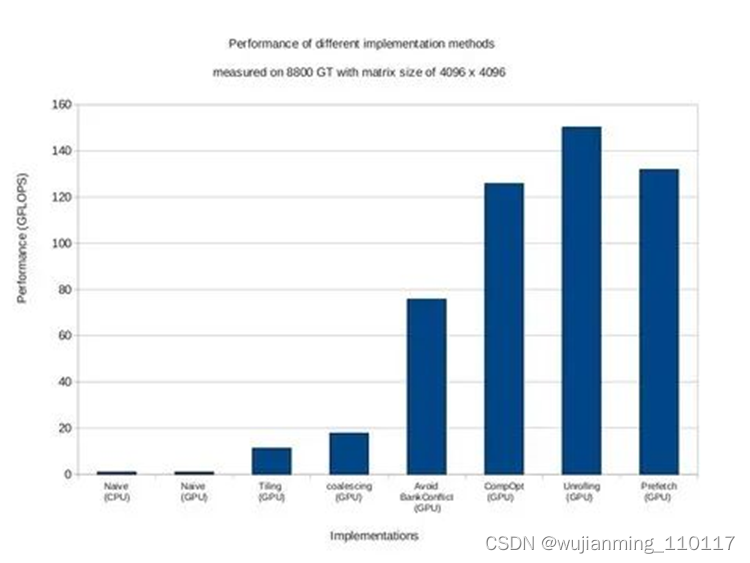
1 关于矩阵乘法的问题描述
首先解决矩阵乘法问题更具体来说是解决GEMM(GEneral Matrix to Matrix Multiplication,通用矩阵乘法)问题。即C=αA*B+βC。其中A、B和C是矩阵。A是M×K矩阵,B是K×N矩阵,C是M×N矩阵。为了方便说明,后续的例子中假设标量alpha=beta=1。
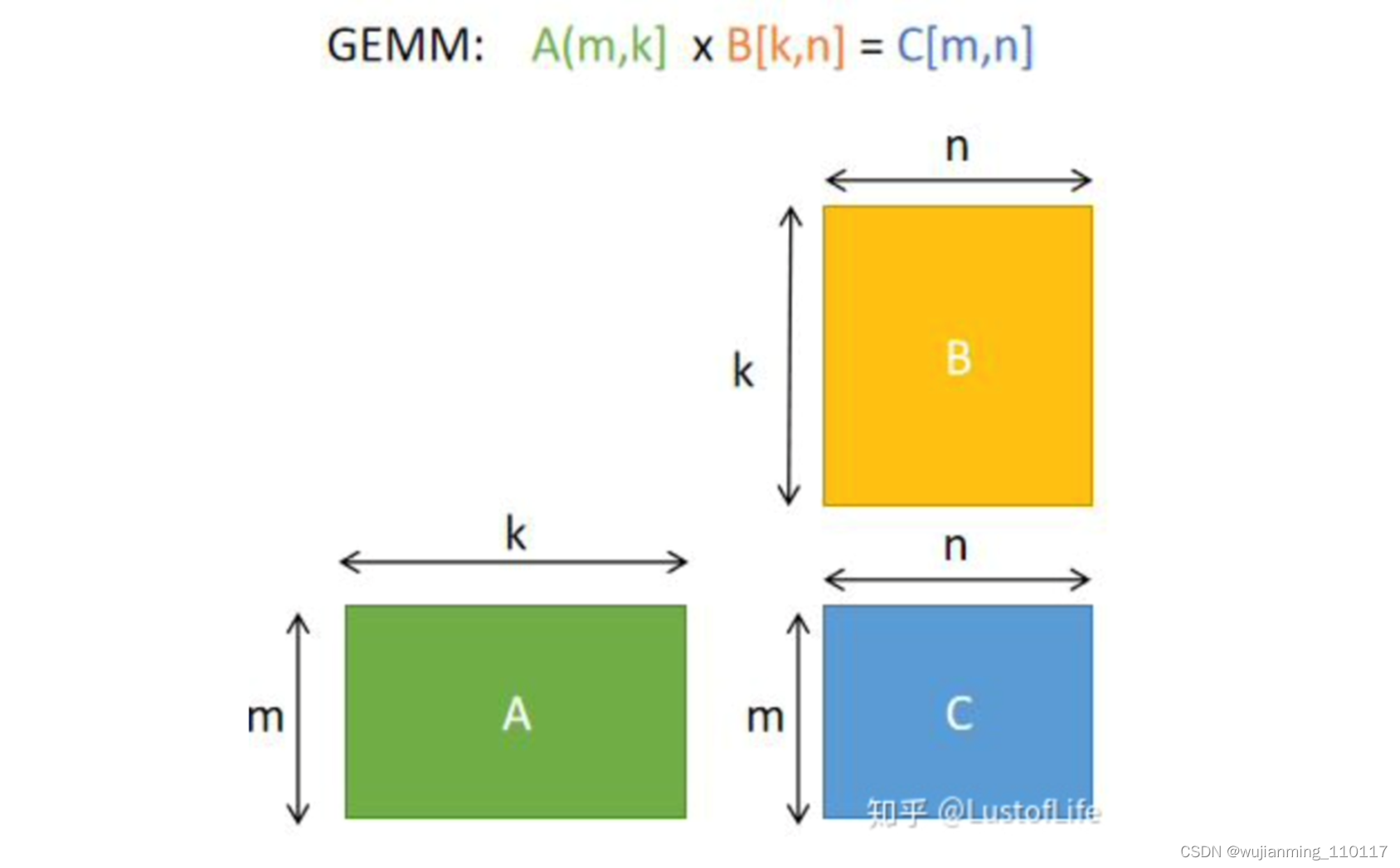
那么如何更高效的进行GEMM呢?
2:优化策略的核心思想
? 1.减小缓存(cached)
? 2.使写入速度跟上指令的计算速度
对于GEMM计算,最直接的想法就是loop,elements相乘再相加
for (int i = 0; i < M; ++i) //---->遍历A的行,行id记做i
for (int j = 0; j < N; ++j) //---->遍历B的列,列id记做j
for (int k = 0; k < K; ++k) //---->在行列i,j确定的前提下,进行对应元素的 相乘 和 加和 ,元素id记做k
C[i][j] += A[i][k] * B[k][j]; //---->最后输出到C的第i,j个元素
对于M=N=K的大型方阵,矩阵乘积中的数学运算数为O(N3),而所需的数据量为O(N2),从而产生N阶的计算强度。然而,利用理论计算强度(heoretical compute intensity)需要将重复使用每个元素O(N)。但是,上面的内积算法依赖于缓存(fast on-chip caches)中保存一个大的工作集,这会导致随着M、N和K增长时,CPU需要来回搬运数据,会累的要死。(不符合减小缓存的思想)
PS:一般来说,求两矩阵内积,K的维度数要远大于N,M(例如SVM中的核函数技巧),所以将大计算量的K维放在内循环不是一个聪明的决定。
一个更好的公式是通过构造K维上的循环作为最外层的循环来置换循环嵌套。这种形式的计算一次加载a列和B行,计算其外积,并将此外积的结果累加到矩阵C中。此后,a列和B行的结果将不再使用。
for (int k = 0; k < K; ++k) // K dimension now outer-most loop
for (int i = 0; i < M; ++i)
for (int j = 0; j < N; ++j)
C[i][j] += A[i][k] * B[k][j];
更进一步思考,如何进一步减少寄存空间的缓存大小?
上述方法的一个问题是,它要求矩阵C的所有M-by-N元素都是激活的,以存储每个乘法累加指令的结果。这样很难保证内存中的写入速度能够跟上CPU中的计算速度。
如何去使得内存的写入速度与计算乘法累加指令的速度一样快呢?
– 采用分块(Tile)的策略
重点来了,
首先 ,我们可以通过将矩阵C的工作空间Partitioning为大小为(Mtile-by-Ntile)的Tile来矩阵C的工作空间大小(the working set size of C), 这些Tile的大小需要与存储器(on-chip memory)相适应。
然后,我们将用外积代替内积的策略应用到每一块Tile上。就像以下循环嵌套这样。
for (int m = 0; m < M; m += Mtile) // iterate over M dimension
for (int n = 0; n < N; n += Ntile) // iterate over N dimension
for (int k = 0; k < K; ++k) //----> like above example
for (int i = 0; i < Mtile; ++i) // compute one tile
for (int j = 0; j < Ntile; ++j) {
int row = m + i;
int col = n + j;
C[row][col] += A[row][k] * B[k][col];
}
对于C上的每一块Tile,都只取了一次A和B中的Tiles,使其达到*O(N)*的计算强度。示意图就类似下面这样。(如果对 global memory / shared memory / register file/ SM cores 不太清楚的话,还是建议好好研究研究一下,对后续的优化策略理解很有帮助!)
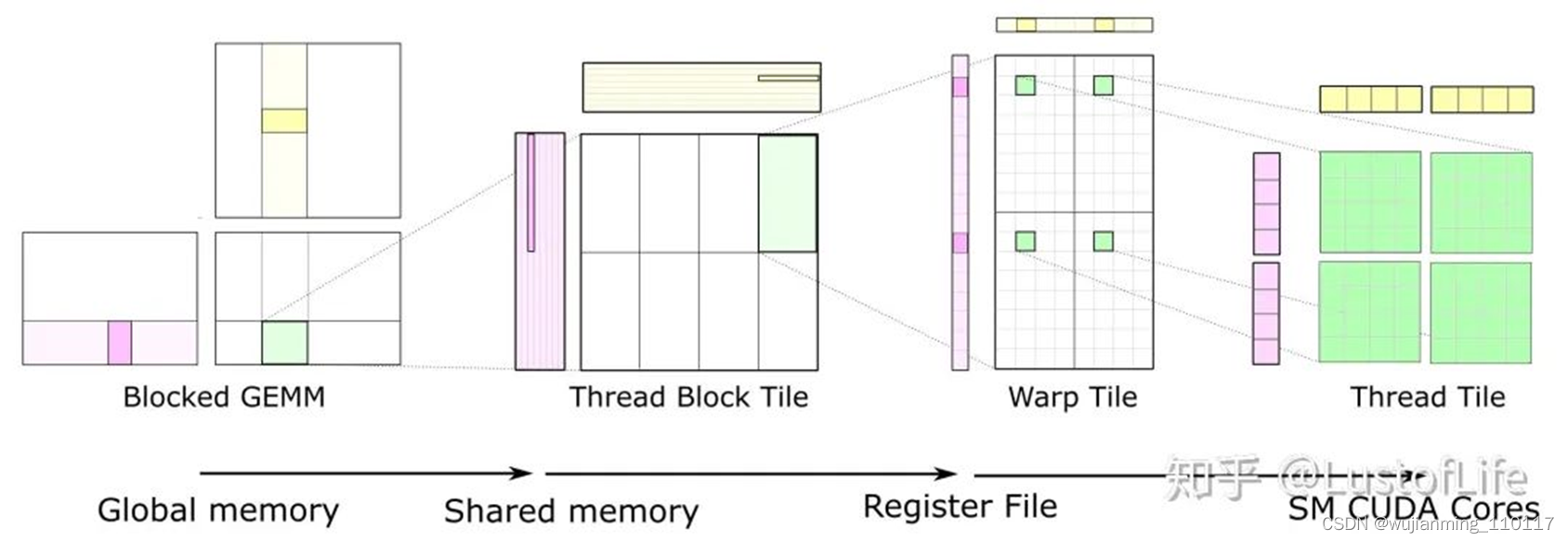
对于GPU来说,The size of each tile of C may be chosen to match the capacity of the L1 cache or registers of the target processor, and the outer loops of the nest may be trivially parallelized. This is a great improvement !
Here, you can see data movement from global memory to shared memory (matrix to thread block tile), from shared memory to the register file (thread block tile to warp tile), and from the register file to the CUDA cores for computation (warp tile to thread tile).
参考文献链接
https://www.zhangshilong.cn/work/35703.html
https://mp.weixin.qq.com/s/7lSuTnoi3V-8-BMP8m53tg
Matrix Multiplication CUDA——https://ecatue.gitlab.io/gpu2018/pages/Cookbook/matrix_multiplication_cuda.html
https://mp.weixin.qq.com/s/TaewNgRtValtFEPQafYs-Q
