一般注意力模型
描述一般注意力模型,首先要描述可以使用注意力的模型的一般特征。我们将这种模型称为任务模型,如图:
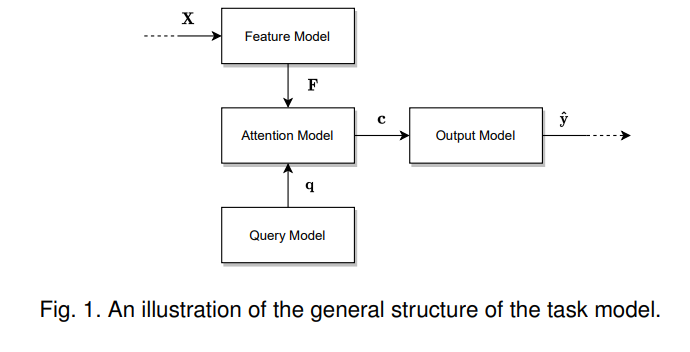
这个模型接受一个输入,执行指定的任务,然后产生所需的输出。例如,任务模型可以是一种语言模型,它以一段文本作为输入,并生成内容的摘要、情感的分类或逐字翻译成另一种语言的文本作为输出。或者,任务模型可以获取一张图像,并为该图像生成描述或分割。
任务模型由四个子模型组成:特征模型( feature model)、查询模型(query model)、注意力模型( attention model)和输出模型(output model)。
特征模型和查询模型,用于为注意力模型提供输入。注意力模型和输出模型用于产生输出。
注意力输入
假设任务模型以矩阵 X ∈ R d x × n x \boldsymbol{X}∈\mathbb{R}^{d_x×n_x} X∈Rdx?×nx?为输入,其中 d x d_x dx?表示输入向量的大小, n x n_x nx?表示输入向量的数量。这个矩阵中的列可以表示句子中的词、图像中的像素、声音序列的特征或任何其他输入集合。
特征模型输入 X \boldsymbol{X} X,输出 n f n_f nf?个特征向量 f 1 , … , f n f ∈ R d f \boldsymbol{f}_{1}, \ldots, \boldsymbol{f}_{n_{f}} \in \mathbb{R}^{d_{f}} f1?,…,fnf??∈Rdf?。其中 d f d_f df?表示特征向量的大小。特征模型可以是循环神经网络(RNN)、卷积神经网络(CNN)、一个简单的嵌入层、对原始数据进行线性变换,或者根本不进行变换等等。本质上,特征模型包含了所有将原始输入 X \boldsymbol{X} X转换为特征向量 f 1 , … , f n f ∈ R d f \boldsymbol{f}_{1}, \ldots, \boldsymbol{f}_{n_{f}} \in \mathbb{R}^{d_{f}} f1?,…,fnf??∈Rdf?(用于输入注意力模型)的操作。
为了确定要重点注意哪些向量,注意力模型还需要查询向量 q ∈ R d q \boldsymbol{q}\in \mathbb{R}^{d_q} q∈Rdq?,其中 d q d_q dq?表示查询向量的大小。查询向量由查询模型得到,通常是根据模型所需的输出类型设计。查询向量告诉注意力模型要注意哪些特征向量。
注意力输出
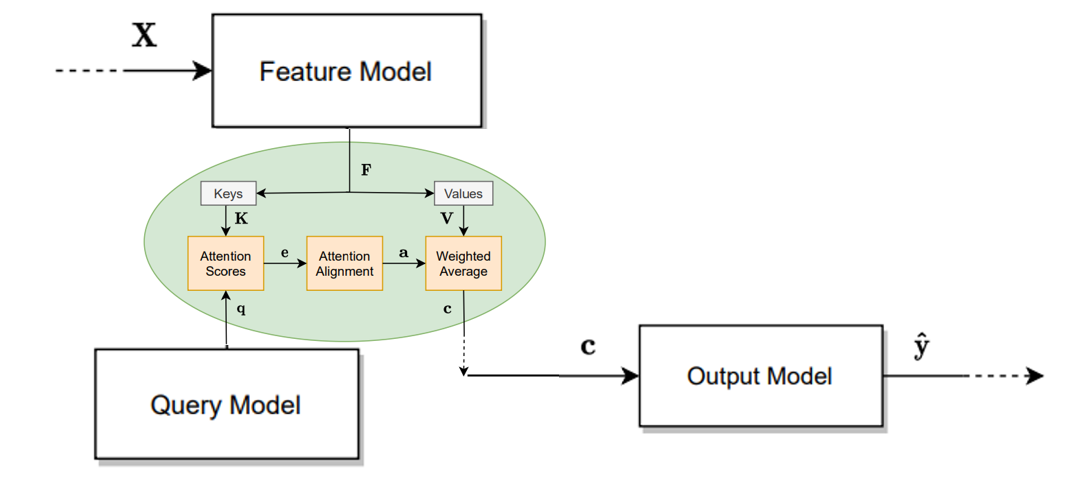
注意力模型由单个或多个的一般注意力模块(general attention modules)组成。下图给出了一般注意力模块的内部机制:
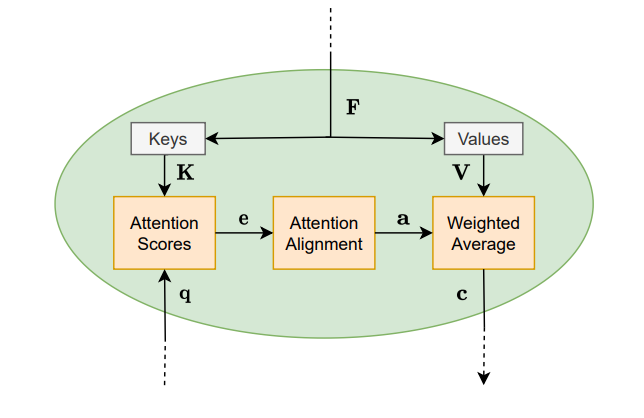
一般注意力模块的输入有查询向量 q ∈ R d q \boldsymbol{q}\in \mathbb{R}^{d_q} q∈Rdq?和由特征向量组成的矩阵 F = [ f 1 , … , f n f ] ∈ R d f × n f \boldsymbol{F}=[\boldsymbol{f}_{1}, \ldots, \boldsymbol{f}_{n_{f}}] \in \mathbb{R}^{d_{f}\times n_f} F=[f1?,…,fnf??]∈Rdf?×nf?。
首先,可以使用权重矩阵 W K ∈ R d k × d f \boldsymbol{W}_K∈\mathbb{R}^{d_k×d_f} WK?∈Rdk?×df?和 W V ∈ R d v × d f \boldsymbol{W}_V∈\mathbb{R}^{d_v×d_f} WV?∈Rdv?×df?对 F \boldsymbol{F} F进行线性变换:
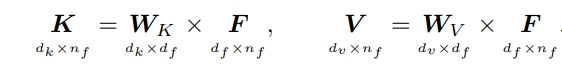
得到键(Keys)矩阵 K = [ k 1 , … , k n f ] ∈ R d k × n f \boldsymbol{K}=\left[\boldsymbol{k}_{1}, \ldots, \boldsymbol{k}_{n_{f}}\right] \in \mathbb{R}^{d_{k} \times n_{f}} K=[k1?,…,knf??]∈Rdk?×nf?和值(Values)矩阵 V = [ v 1 , … , v n f ] ∈ R d v × n f \boldsymbol{V}=\left[\boldsymbol{v}_{1}, \ldots, \boldsymbol{v}_{n_{f}}\right] \in \mathbb{R}^{d_{v} \times n_{f}} V=[v1?,…,vnf??]∈Rdv?×nf?,其中 d k d_k dk?和 d v d_v dv?分别表示键向量( K \boldsymbol{K} K的列)和值向量( V \boldsymbol{V} V的列)的大小。
这两个权重矩阵可以是可训练的或者预先指定的。例如,可以选择将 W K \boldsymbol{W}_K WK?和 W V \boldsymbol{W}_V WV?都定义为单位矩阵,这将保留原始的特征向量。还有其他定义键和值的方法,例如用不同的 F \boldsymbol{F} F产生键和值,不过要保证 K \boldsymbol{K} K和 V \boldsymbol{V} V的列数相同。
注意力模块的目标是得到 V \boldsymbol{V} V中值向量的加权平均值。用于产生此输出的权重是通过注意力打分(attention scoring)和对齐(alignment )步骤获得的。
查询向量
q
\boldsymbol{q}
q和键矩阵
K
\boldsymbol{K}
K用于计算注意力得分向量
e
=
[
e
1
,
…
,
e
n
f
]
∈
R
n
f
\boldsymbol{e}=\left[e_{1}, \ldots, e_{n_{f}}\right] \in \mathbb{R}^{n_{f}}
e=[e1?,…,enf??]∈Rnf?。这是通过打分函数score()完成的:
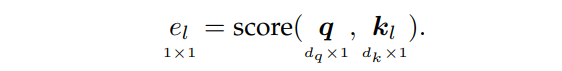
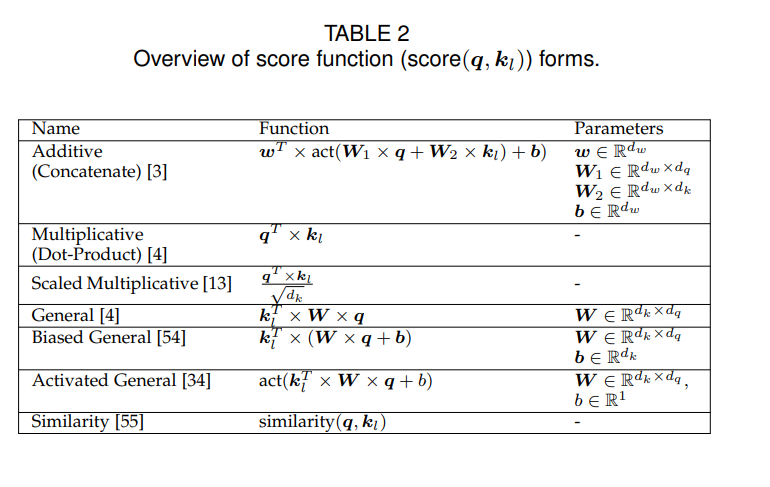
查询 q \boldsymbol{q} q表示对信息的请求。注意得分 e l e_l el?表示根据查询 q \boldsymbol{q} q,键向量 k l \boldsymbol{k}_l kl?中包含的信息有多重要。表2给出了各种注意力打分函数。
注意力得分的范围通常在
[
0
,
1
]
[0,1]
[0,1]之外。因此,还需要通过对齐层归一化注意力分数,常用Softmax函数:
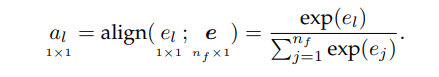
其中 a l ∈ R 1 a_l∈\mathbb{R}^1 al?∈R1为第 l l l个值向量对应的注意力权值。
注意力权重为注意力模块提供了一个相当直观的解释。每个权重都直接表明每个特征向量相对于其他特征向量的重要性。
通过注意力权重向量
a
=
[
a
1
,
…
,
a
n
f
]
∈
R
n
f
\boldsymbol{a}=\left[a_{1}, \ldots, a_{n_{f}}\right] \in \mathbb{R}^{n_{f}}
a=[a1?,…,anf??]∈Rnf?对值矩阵
V
\boldsymbol{V}
V各列进行加权平均,得到上下文向量(context vector)
c
∈
R
d
v
\boldsymbol{c}∈ \mathbb{R}^{d_v}
c∈Rdv?:
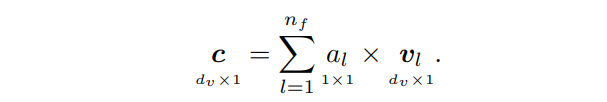
最后,上下文向量输入输出模型得到输出 y ^ \boldsymbol{\hat{y}} y^?
这个输出模型将上下文向量转换为输出预测。例如,它可以是一个简单的softmax层,将上下文向量 c \boldsymbol{c} c作为输入:
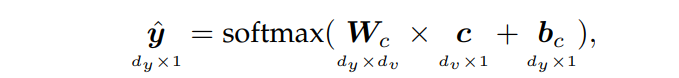
其中 d y d_y dy?是输出向量的大小, W c ∈ R d y × d v \boldsymbol{W}_c\in \mathbb{R}^{d_y\times d_v} Wc?∈Rdy?×dv?和 b c ∈ R d y \boldsymbol{b}_c\in \mathbb{R}^{d_y} bc?∈Rdy?是可训练参数。
参考:
[1] A General Survey on Attention Mechanisms in Deep Learning https://arxiv.org/pdf/2203.14263v1.pdf
文章预告
