[人工智能]关于SIoU的原理和代码实现(回顾IoU、GIoU、DIoU、CIoU)

论文：https://arxiv.org/pdf/2205.12740.pdf
代码实现（非官方）：https://github.com/xialuxi/yolov5-car-plate/commit/aa41d1819b1fb03b4dc73e8a3e0000c46cfc370b
图片源自视频教程（这个大佬视频教程yyds）：https://www.bilibili.com/video/BV1yi4y1g7ro?p=4

原理：

从最早的IoU到GIoU，再到DIoU和CIoU，现在出现了SIoU

L2损失与 IoU损失的比较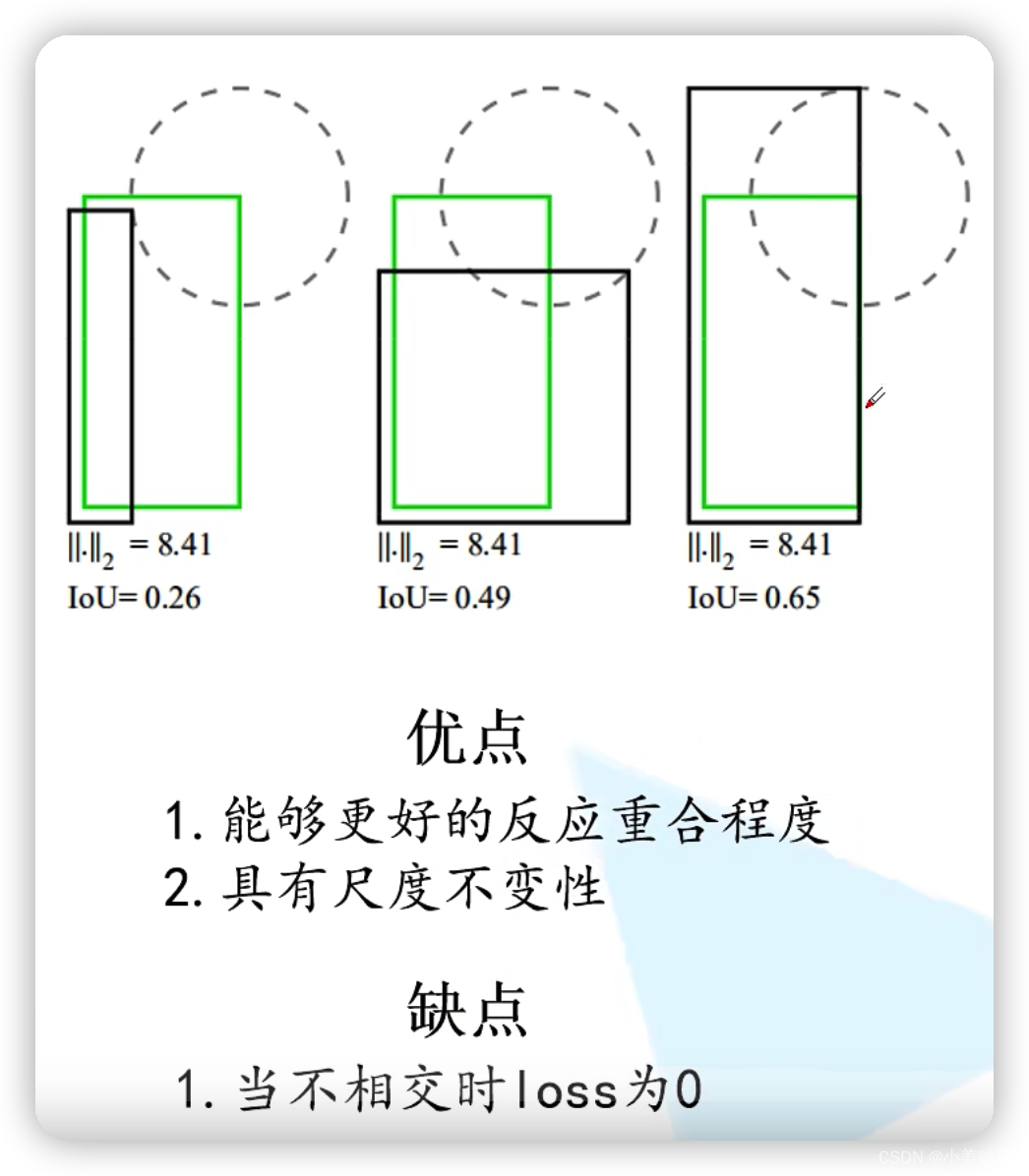

GIoU损失

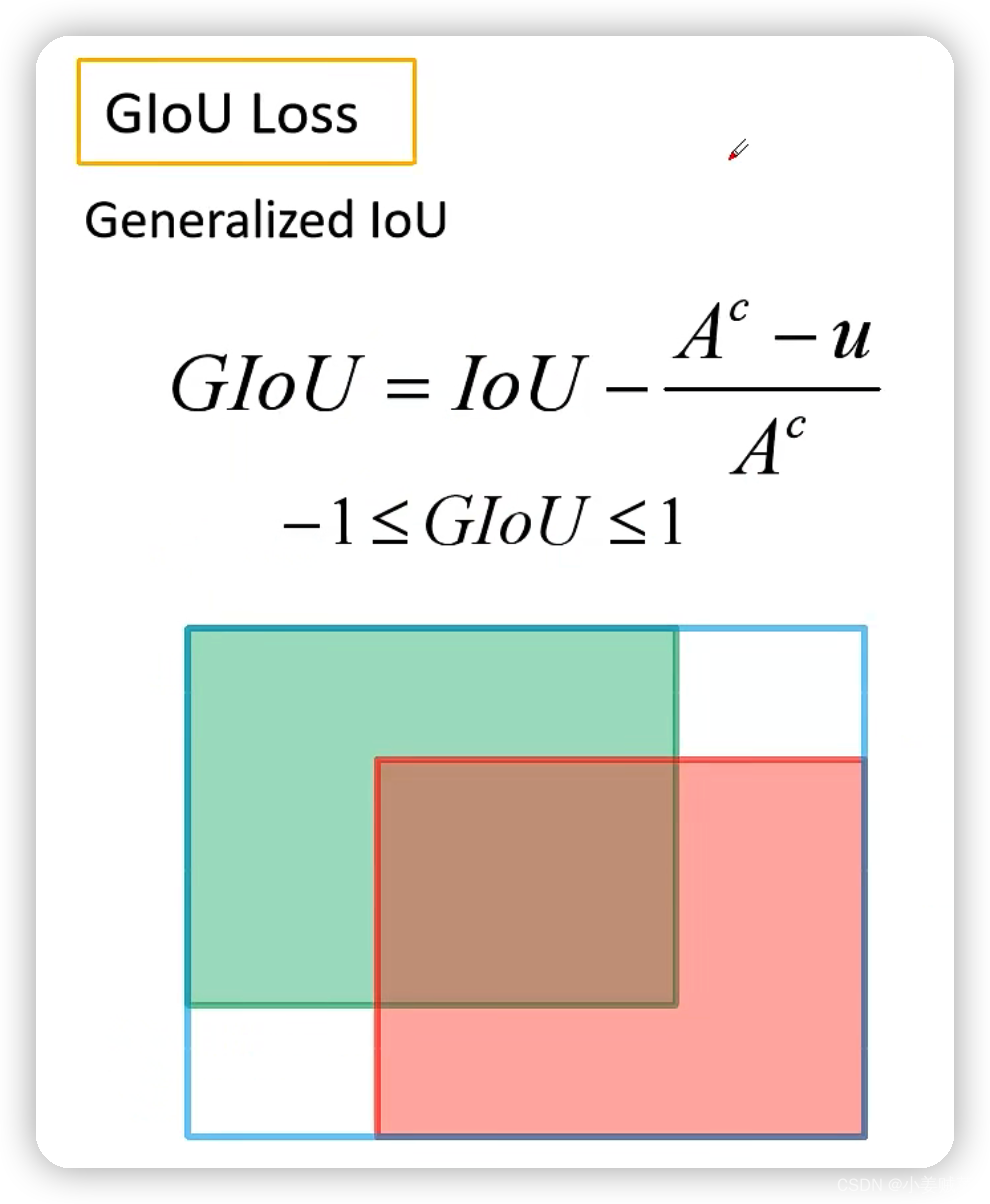
A代表蓝色的框，最大的矩形框。u代表GT和预测框的并集。

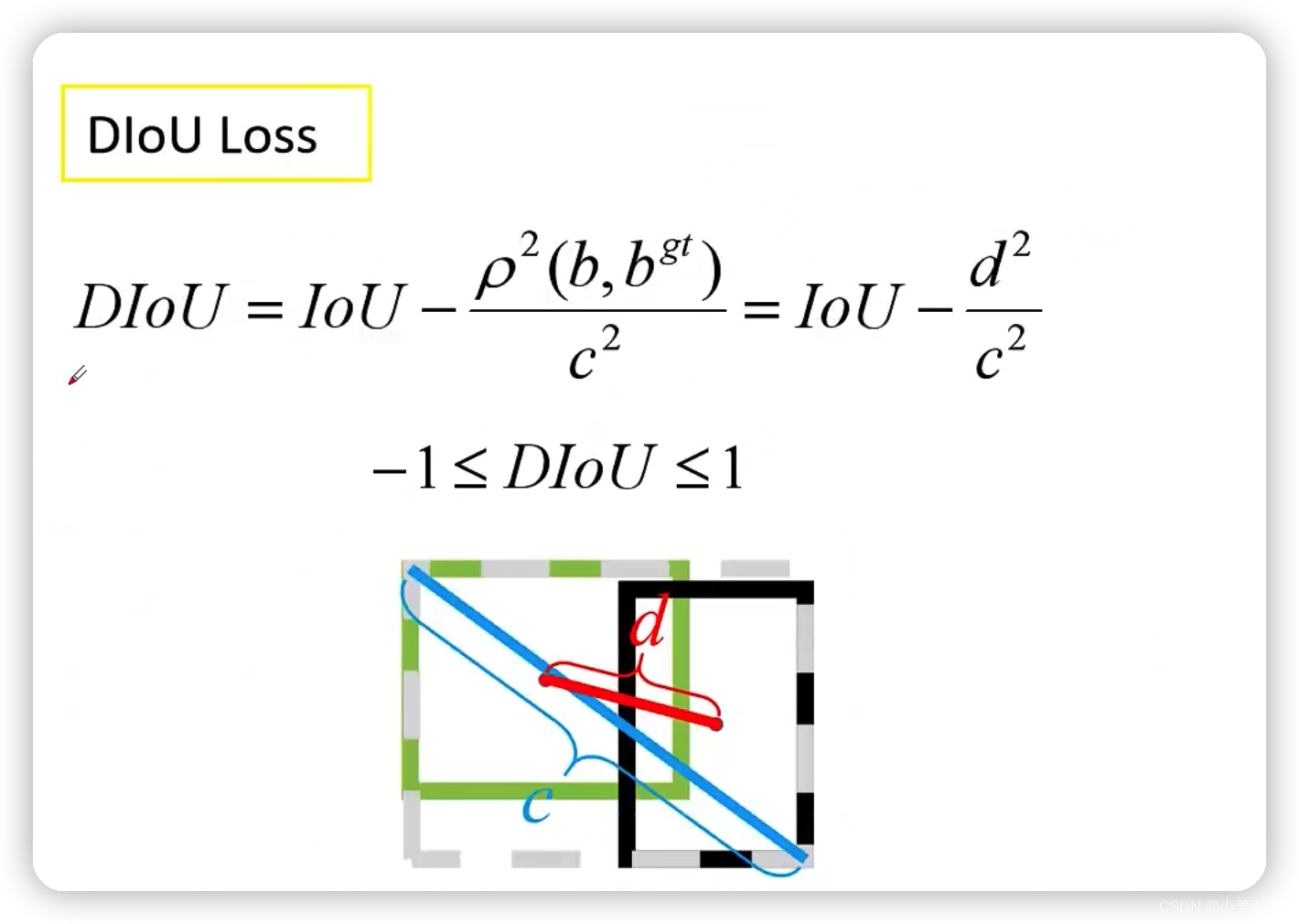
DIoU损失

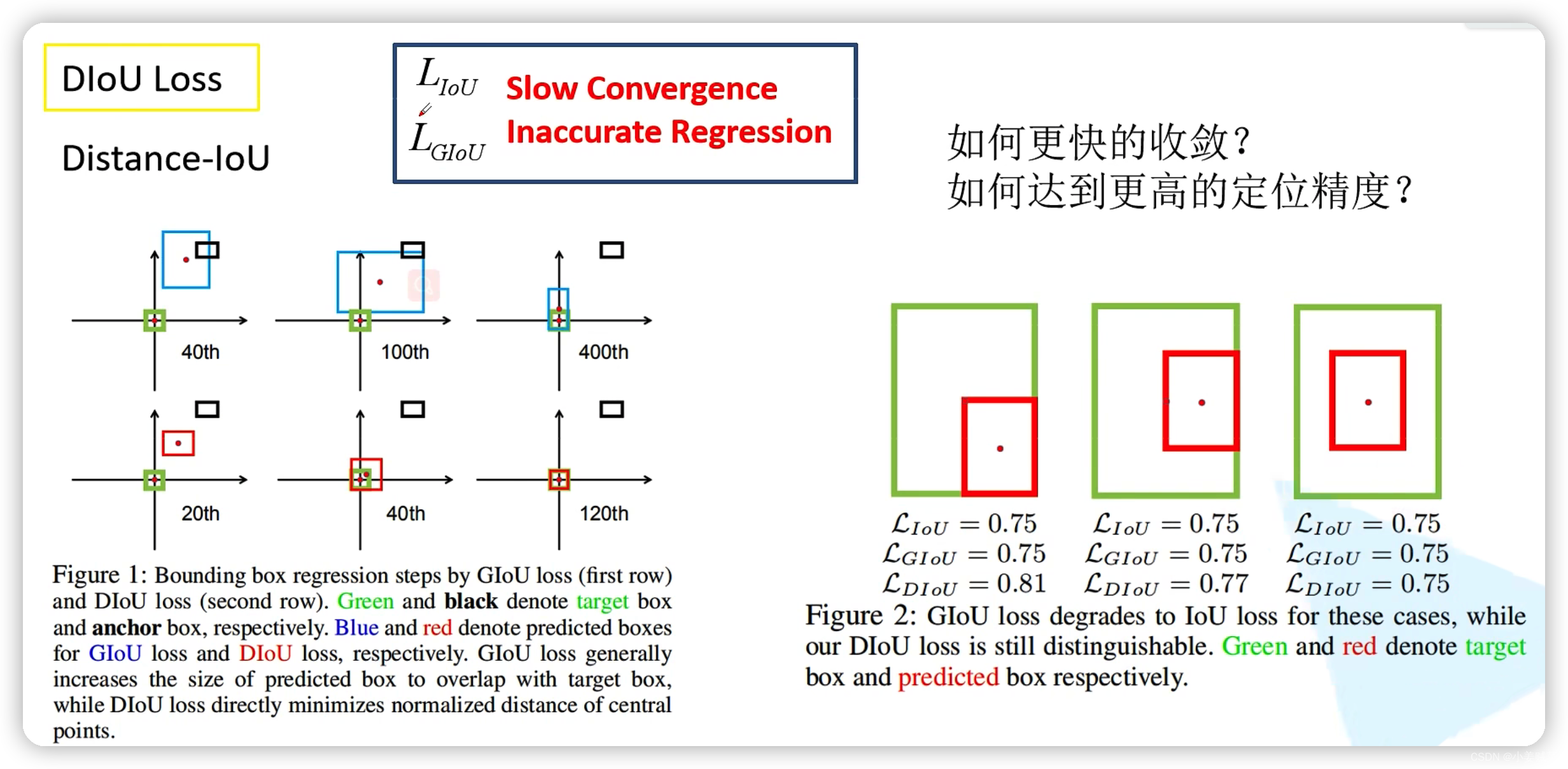
图片一左侧的上面是GIoU，下面的是DIoU：其中黑色的代表anchor，蓝色的代表预测框，绿色的为GT框

CIoU损失

SIoU损失

再上面的基础上考虑了角度
在论文中也重新定义了距离 cost和shape cost，
角度cost 定义如下：

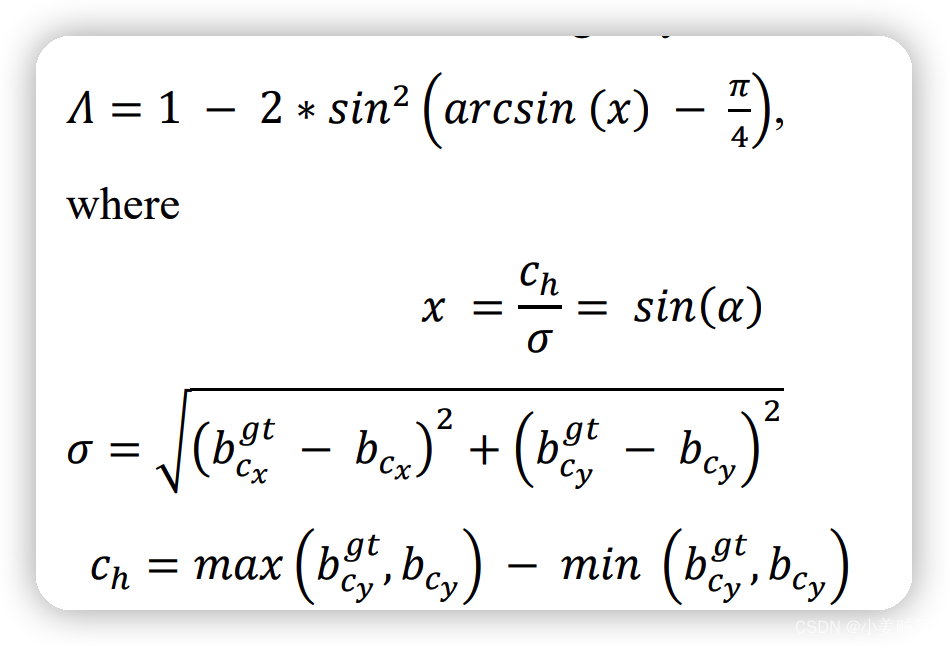
这里我看的很奇怪的一点就是，这个α为啥带入到sin，又带入到反sin，这不是多此一举吗？σ就是两个框的中心距离呗。

距离cost 定义如下：

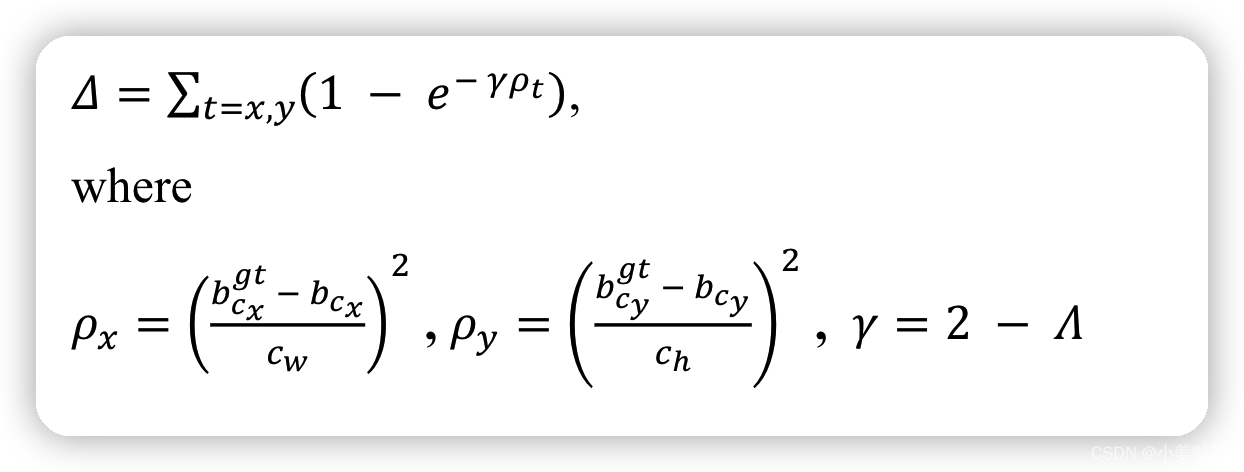
shape cost定义如下：

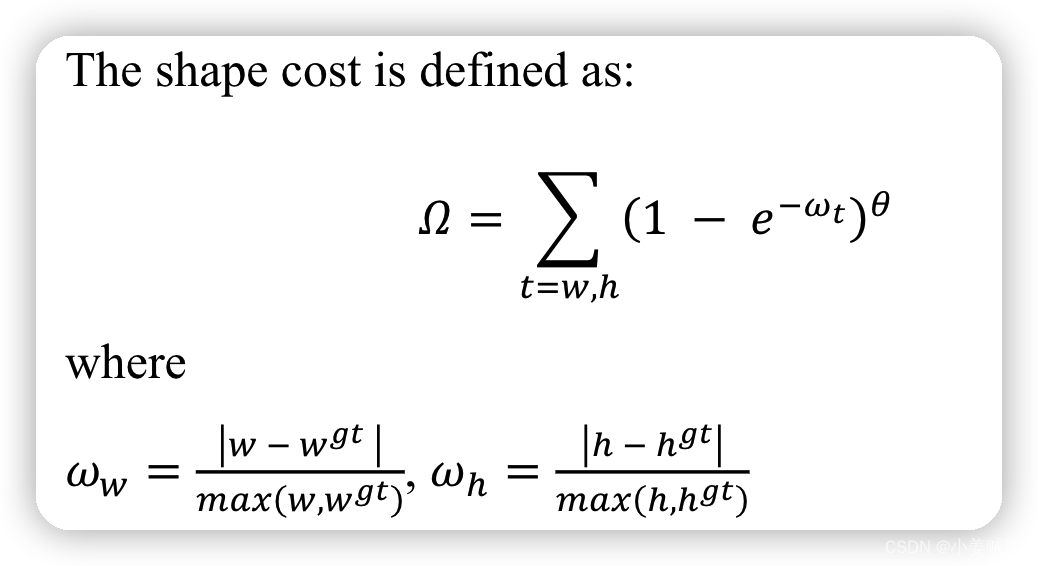
整的lost 定义：

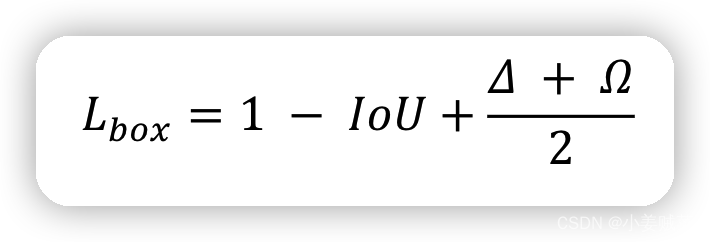
还有很多细节没有分析、挖掘、探讨，这里只是草草的分享下，记录下。

代码实现：

！！！重要的事情说三遍，不是我实现的，不是我实现的，不是我实现的。来自于开头链接的大佬：

        if SIoU:    # SIoU Loss https://arxiv.org/pdf/2205.12740.pdf
            sigma = torch.pow(cw ** 2 + ch ** 2, 0.5)
            sin_alpha_1 = ch / sigma
            sin_alpha_2 = cw / sigma
            threshold = pow(2, 0.5) / 2
            sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)
            # angle_cost = 1 - 2 * torch.pow( torch.sin(torch.arcsin(sin_alpha) - np.pi/4), 2)
            angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - np.pi / 2)
            rho_x = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) / cw) ** 2
            rho_y = ((b2_y1 + b2_y2 - b1_y1 - b1_y2) / ch) ** 2
            gamma = 2 - angle_cost
            distance_cost = 2 - torch.exp(-1 * gamma * rho_x) - torch.exp(-1 * gamma * rho_y)
            omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)
            omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)
            shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)
            return iou - 0.5 * (distance_cost + shape_cost)