[人工智能]神经网络常见评价指标超详细介绍（ROC曲线、AUC指标、AUROC）

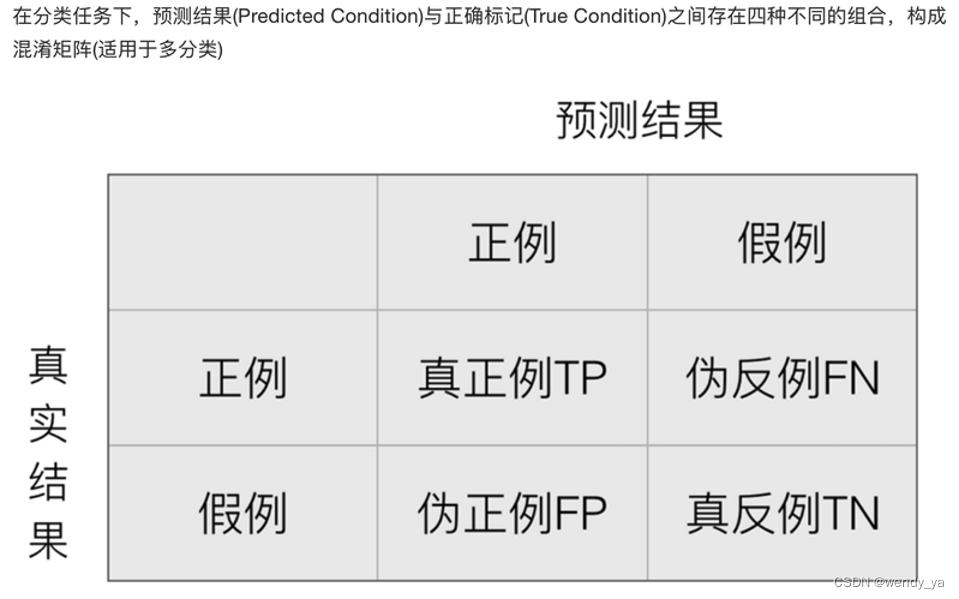
一、基本概念

• 真阳性（TP）：判断为真，实际也为真；
• 伪阳性（FP）：判断为真，实际为假；
• 伪阴性（FN）：判断为假，实际为真；
• 真阴性（TN）：判断为假，实际也为假；
  
• TPR（真阳性率）：在所有实际为真的样本中，被正确预测为真的概率：
  $TPR=\frac{TP}{TP+FN}$
• FPR（伪阳性率）：在所有实际为假的样本中，被错误预测为真的概率；
  $FPR=\frac{FP}{FP+TN}$

二、ROC曲线

ROC曲线：接受者操作特征曲线（receiver operating characteristic curve）。
ROC空间将伪阳性率（FPR）定义为 X 轴，真阳性率（TPR）定义为 Y 轴。
从 (0, 0) 到 (1,1) 的对角线将ROC空间划分为左上／右下两个区域，在这条线的以上的点代表了一个好的分类结果（胜过随机分类），而在这条线以下的点代表了差的分类结果（劣于随机分类）。
完美的预测是一个在左上角的点，在ROC空间座标 (0,1)点，X=0 代表着没有伪阳性，Y=1 代表着没有伪阴性（所有的阳性都是真阳性）；也就是说，不管分类器输出结果是阳性或阴性，都是100%正确。一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线（也叫无识别率线）上的一个点；最直观的随机预测的例子就是抛硬币。

但是仔细想想，实际上越接近曲线表示分类结果越差，越接近左上角和右下角则表示分类结果越好。不难理解，越接近曲线，表示分类的伪阳性率和真阳性率越接近，则表示分类器越难判断出是真实样本还是虚假样本；而越接近左上角代表分类器很容易正确判断出真实样本和虚假样本，越接近右下角则代码越容易将真实样本判断为虚假样本，若将其取反，则会同样会越接近左上角。

两种ROC曲线哪个效果更好?

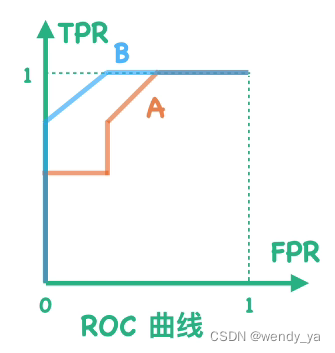
我们希望TP尽可能大，而FP尽可能小，因此曲线越靠近左上角效果越好，即B分类效果比A分类效果更好。

三、AUROC（AUC指标）

AUROC（Area Under the Receiver Operating Characteristic curve，接受者操作特征曲线下面积，即ROC曲线下面积）

AUROC通过接受者操作特征曲线（receiver operating characteristic curve）与坐标轴之间的?积??来反应分类器的性能，其意义在于：
因为是在1x1的方格里求面积，AUROC必在0~1之间。
若随机抽取一个阳性样本和一个阴性样本，分类器正确判断阳性样本的值高于阴性样本之机率。
简单说：AUROC值越大的分类器，正确率越高。

从AUROC判断分类器（预测模型）优劣的标准：

• AUROC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器；
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值；
• AUC = 0.5，跟随机猜测一样（例：丢硬币），模型没有预测价值；
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测；

其意义可以理解为均匀抽取的随机阳性样本（正样本）排名在均匀抽取的随机阴性样本（负样本）之前的期望。AUROC是?个介于0到1之间的数值，当AUROC值越接近于1时，表示分类器可以较好的分类正负样本。

四、实例介绍

4.1 公式实现

考虑标签label和预测值pred，其数值如下：
label = [1, 0, 0, 0, 1, 0, 1, 0]
pre = [0.9, 0.8, 0.3, 0.1, 0.4, 0.9, 0.66, 0.7]

其散点图如下：

怎样才能通过概率得到预测的类别呢？
通常我们需要设置一个阈值，这里以0.5为例，当概率大于等于0.5时，分类器认为这个为真实类别；当概率小于0.5时，分类器认为这个不是真实类别，如下图所示：

我们可以根据这个图得到当阈值为0.5时的混淆矩阵：

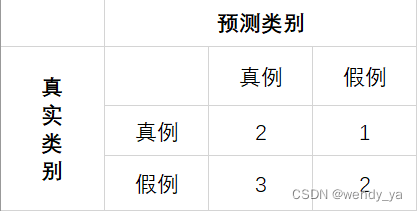
实际上阈值可以取[0,1）之间的任意值，理论上可以取无数个混淆矩阵，而把所有的混淆矩阵表示在同一个二维空间中的方法称为ROC曲线。

回到之前的栗子，当阈值取[0,0.1)时，分类器任务所有的都是真实类别，其混淆矩阵如下：

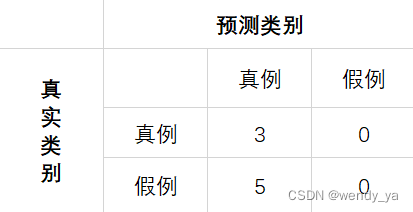
$TPR=\frac{TP}{TP+FN}=\frac{3}{3+0}=1$
$FPR=\frac{FP}{FP+TN}=\frac{5}{5+0}=1$
对应到二维空间中就是坐标为(1,1)的点

当阈值取[0.1,0.2)时，我们可以得到新的混淆矩阵如下：

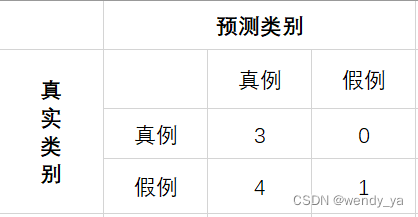
$TPR=\frac{TP}{TP+FN}=\frac{3}{3+0}=1$
$FPR=\frac{FP}{FP+TN}=\frac{4}{4+1}=0.8$
对应到二维空间中就是坐标为(0.8,1)的点

以此类推…

最终得到所有坐标点，根据这些坐标点，连成一条线如下图所示：

AUROC（AUC指标）即为右下角的面积：
$\frac{1}{3}?0.2/2+\frac{1}{3}?0.4+0.4?1=0.566666666666666666$

4.2 代码实现

计算AUROC指标有两种方法：
方法1：自定义函数

• 若Sim测试 > Sim不存在，则数值的分子加1（此时证明预测效果良好）；
• 若 Sim测试 = Sim不存在 ，则数值的分子加0.5（此时相当于随机选择）；
• 若Sim测试 < Sim不存在，则数值的分子加0。
  （Sim表示相似值）
  数值的分母是测试集中的边的相似值与不存在的边的相似值比较的次数。比如测试集中2条边，不存在中3条边，那么比较次数就是6次。
  AUC指标即为数值分子与数值分母的比值，AUC大于0.5的程度衡量了算法在多大程度上优于随机选择的算法。

定义AUC函数：

def AUC(label, pre):
    # 计算正样本和负样本的索引，以便索引出之后的概率值
    pos = [i for i in range(len(label)) if label[i] == 1]   #正样本索引
    neg = [i for i in range(len(label)) if label[i] == 0]   #负样本索引
    auc = 0
    for i in pos:
        for j in neg:
            if pre[i] > pre[j]:
                auc += 1
            elif pre[i] == pre[j]:
                auc += 0.5

    return auc / (len(pos) * len(neg))

调用函数：

if __name__ == '__main__':
    label = [1, 0, 0, 0, 1, 0, 1, 0]
    pre = [0.9, 0.8, 0.3, 0.1, 0.4, 0.9, 0.66, 0.7]
    print(AUC(label, pre))

运行结果：
0.5666666666666667

方法2：使用sklearn算法库的包

导入roc_curve,和auc包：

# 导入sklearn算法库中的包
from sklearn.metrics import roc_curve, auc

主程序：

label = [1, 0, 0, 0, 1, 0, 1, 0]
pre = [0.9, 0.8, 0.3, 0.1, 0.4, 0.9, 0.66, 0.7]
'''
label是列表形式，对应方法1中的label形式
pre是列表形式，对应方法1中的pre形式
'''
fpr, tpr, th = roc_curve(label, pre, pos_label=1)
print('sklearn', auc(fpr, tpr))

运行结果：
0.5666666666666667

ok，以上便是本文的全部内容了，如果对你有所帮助，记得点个赞哟~

参考：

1. https://baike.sogou.com/v472808.htm
2. https://blog.csdn.net/Queen0911/article/details/109693384
3. https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html#sklearn.metrics.roc_curve

相关资源可参考：https://download.csdn.net/download/didi_ya/85564779