一、脉冲耦合神经网络(PCNN)图像特征提取简介
1 引言
随这生物神经学的迅速发展及其研究的进一步深入,国外对一种叫做第三代人工神经网络的模型——脉冲耦合神经网络模型——PCNN(Pulse Coupled Neural Network)模型的神经网络的研究从一个悄然兴起阶段进入了升温阶段。并且我们还可以在像IEEE Trans .On Neural Networks等这样的知名刊物上发现有关PCNN论文的印记,但我们很少能发现有关研究中药材显微结构的文章,因为就目前的研究状况来看对其研究还不是很深入完善。由于其具有生物学特性的背景和空间自适应性的特点,使其更加符合视觉系统的研究。因此,脉冲耦合神经网络在数字图像处理:图像的分割、图像的特征提取和目标识别等具有相当可观的应用价值和前景。以下将以脉冲耦合神经网络作为基础结合其他特征提取与识别方法完成对中药材显微图像的相关特征提取。
2 PCNN概述
2.1 PCNN原理
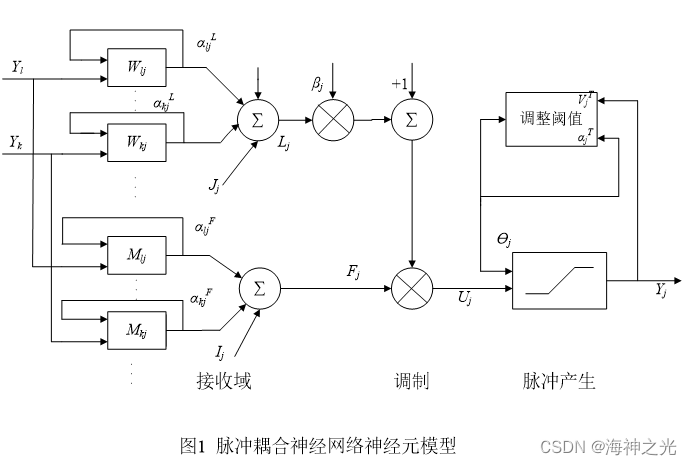
1990年,由Eckhorn等人提出并且发起的对猫等哺乳动物的视觉皮层神经元脉冲振荡(同步振荡)现象的研究[[[]Eclhorn R, Reitboeck H J, Arndt Metal.Feature Linking Vial Synchronization Among Distributed Assemblies: Simulation of Results from Cat Cortex[J]. Neural Comput., 1990, 2(3): 293-307.]]促使了脉冲耦合神经网络(PCNN—Pulse Coupled Neural Network)的初步形成和迅速发展。Eckhorn发现刺激神经元输入会引起视觉皮层的不同区域出现此种现象,然而这些区域的这种局部特性却具有相似性。因此,他认为视觉系统中存在某种机制,能够将局部性质联系起来成为一种整体特性,即以相似性集群的特性。并进一步提出了一种展现脉冲发放现象的脉冲连接模型。而后Johson发表了论文,阐述了PCNN的一种周期波动现象和PCNN在图像处理中具有旋转、尺度、信号扭曲和信号强度不变性。并先后对Eckhorn提出的网络模型进行了改进,由此得到了如今被广泛应用的脉冲耦合神经网络(PCNN)模型。PCNN是由若干神经元互连而成的、以迭代运算为主的单层二维局部连接的反馈型的脉冲神经网络模型。与其它的人工神经网络相比有着显著的区别,PCNN可以进行无监督自学习,其参数不需要进行提前训练,属于第三代神经网络模型,具有优良的自学习图像分割和自学习图像特征提取。因此非常适合实时图像处理的环境下。图1为PCNN的神经元模型。
其相应数学方程。
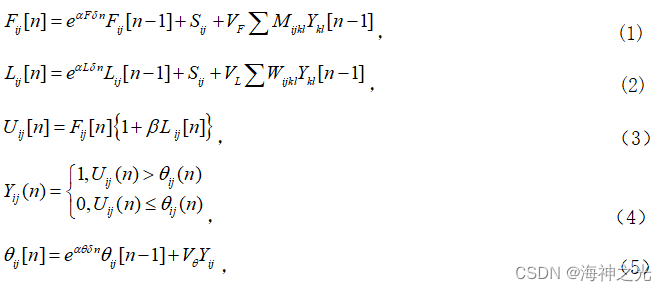
由图1可知,神经元模型共分为三部分:树突(接收域)、非线性连接调制和脉冲产生部分。接收域接收来自神经元与外部的输入。调制部分是将来自L通道的信号加一个正的偏移量后与来自F通道的信号进行相乘调制,模型中正偏移量归一化为1,为连接强度。脉冲产生部分是由对网络输入进行漏电容积分的变阈值特性和起抑制神经元作用的硬限幅函数组成。式中S为激励,F为反馈,L为连接,U为内部运动特征,Y为脉冲输出,?为动态阈值,局部连接M与W通常为定值服从高斯分布。但是鉴于网络参数的难以确定等困难的存在,进而出现了神经元的简化模型,见图2:
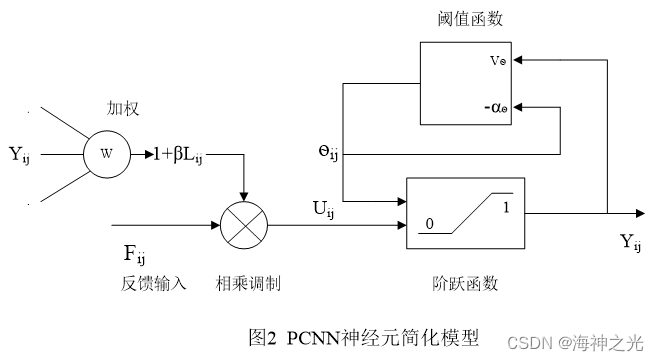
其相应数学方程:
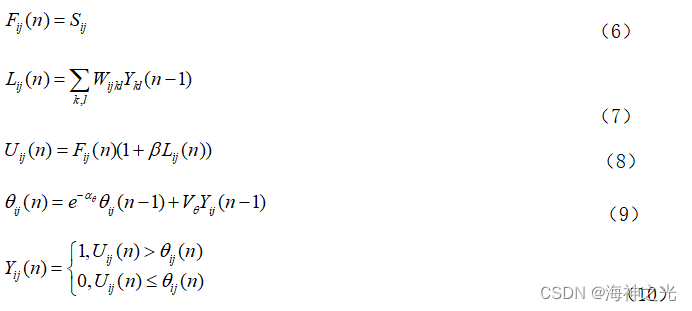
2.2 PCNN的基本特性
2.2.1 脉冲耦合特性
脉冲耦合特性是PCNN 最基本的特性,即神经元的输出和来自其他神经元的输入都为脉冲。
2.2.2 阈值变换特性
构成 PCNN 神经元的阈值受时间的影响和神经元输出的影响。当神经元输出脉冲时,阈值就随脉冲输出的变化而变化。而PCNN所具有的周期性点火的能力,也正是由这种动态阈值特性提供的。
2.2.3 PCNN的差异性
PCNN 中的神经元与构成其它神经网络的神经元存在着根本性的区别。与传统的人工神经网络(如BP、Hopfield等神经网络)相比,其差异主要体现在网络的拓扑结构、权值确定等方面,但是构成这些神经网络的单个神经元结构和功能是相似的,通常都是将输入信号的加权和与阈值进行比较,得到输出。
2.2.4 捕获与非线性调制特性
捕获特性是PCNN最具代表性的基本特性。正因为存在神经元之间的捕获功能,某一先点火的神经元会激励并且带动邻近神经元而提前点火,但还是会有例外发生,然而这些现象的处理会更加凸现PCNN网络处理突发事件的能力。
2.2.5 同步脉冲发放特性
PCNN 中,相邻神经元可以发放同步脉冲。然而形成PCNN非常重要的性质是,利用相似性集群特性产生同步脉冲发放[[[]秦海林,王峥涛等.中药材特征性总成分指纹鉴定[J].中国药科大学.河南省科学院.中国中药杂志.2001.1:4-8.]]。
2.2.6 自动波特性
利用PCNN进行处理时,单个神经元产生的脉冲可以在网络中实现扩散传播,形成脉冲波。当一个神经元点火并发出脉冲后,若能在一定时间段对其进行抑制,而在这一时间段内,因当前神经元的点火而通过耦合连接触发相邻神经元使其激活且点火,但由于各神经元的点火周期不同,会使不同神经元在不同时间发放脉冲,并且这一过程将一直持续进行。最初点火的神经元所产生的脉冲就在网络中扩散传播,从而在PCNN网络中形成以先点火神经元为波动中心的自动波的传播。
2.2.7 畸变不变性特性
在一定条件下,PCNN 对同一图像在不同情况下的处理结果具有稳定性,若使 PCNN 中神经元接收域的联结权具有一定的对称性,则在图像识别时,PCNN 对图像的处理结果具有旋转不变性、强度不变性、尺度不变性及扭曲不变性。
3 体视学
20世纪80年代以来,由丹麦科学家冈德森(Gundersen)建立的现代体视学(Stereology)或者叫立体学为准确定量研究物体形态结构提供了一个可靠的方法。我国于1988年也成立了中国体视学学会(CSS——Chinese Society for Stereology)以及生物医学体视学学会(BSS)。在此之后,研究人员对国际性与全国性的学术会议的参与热情高涨,在体视学技术应用分析方面发表的论文也越来越呈现出多样性。随着生物医学界对物体定量研究的逐步深入,体视学技术的运用潜力将会进一步显现出来。体视学是形态学与数学交叉形成的一门新兴学科,通过二维结构信息定量测量分析三维形态结构特征。体视学的无偏、快速、精确、无损伤性和重复性高等特点,使得其被广泛地运用于细胞生物学和组织学等生物学领域的定量分析和统计中。
3.1 体视学原理
体视学是通过二维图像的定量分析获取数据以定量描述三维几何,并在微观组织分析中加以应用的方法[[[]Exner.HE.Stereologyand3Dmicroscopy:useful alternativesor competitors in the quantitative analysis of microstructures[C]//Proceedings of XIth International Congress for Stereology Beijing Conference,Beijing,Nov.4 -8, 2003:2.]],也可以说是建立从组织的截面所获得的二维测量量与描述其自身组织结构的三维参数之间关系的数学方法的科学。它的发展主要是基于卡瓦列里原理和德莱塞原理。卡瓦列里原理是用来估算任意形状粒子体积的方法,即利用粒子的一组等距随机的平行截面的总面积与截面间距的乘积值来估算出该粒子体积;而德莱赛原理是最基本、最实用的原理之一,其描述的内容是待测物所占体积百分数等于在观察试样中所占的面积,等于观察线段中所截线段的百分比,也等于在观测的总点数中所占的点数百分比。
3.2 体视学参数及测量工具
体视学是一套包含体视学参数、测量工具和误差分析的完整测量系统。体视学基本参数分四类:1、密度参数:定量描述单位参照物中某种结构成分的形态和数量;2、形状参数:定量表达组织结构的形状;3、尺寸参数:定量反映组织结构成分的大小;4、分布参数:定量衡量组织结构的空间分布。除了以上四种基本参数外,还可以用粒子总数、结构成分的总表面积和总体积等参数来进行补充描述[[[]申洪.生物体视学——形态学、数学及生物物理学间的交叉学科[J].生物物理学报,2006,22(1):484.]]。
体视学将体视网格作为其测量工具的,体视网格有以下四类:1、点测试格:主要用来分析面积、体积分数以及总体积等参数;2、多功能测试格:主要用来分析周长、形状因子和表面积等参数;3、圆弧摆线测试格:通常用来分析垂直剖面和有层次样品的体积分数和表面积等参数;4、Merz曲线测试格:主要用来测试各向同性和各向异性组织结构的体积分数、表面积和数密度等参数
3.3 体视学的特点
为了避免断层插值和绘制等繁冗的过程,体视学技术不建立物体的立体形态,而是根据二维图像直接推导出其三维数据,从而为定量分析省去了较多的时间。此外,体视学还以无偏性为特点。这种无偏性常常被人们理解为体视学原理的估算方法是无偏的。首先,体视网格采样时必须满足均匀随机取样原则,即组织样本切片及视野应尽可能的取自器官组织内任何部位,体视网格应尽可能的覆盖于组织任何部位;其次,以设计依赖法为主要测量方法,即通过切片方向以及测线方向实现各向同性随机测量。值得关注的是,体视学测量需要分析的试样中所有的特征信息都必须包含在体视学测量的试样当中。
4 Hu矩不变矩
图像不变矩可以分为灰度直方图不变矩和空间不变矩,空间不变矩对图像平移、旋转、比例变化、对比度变化具有很好地恒定性。不变矩就是一种通过提取具有平移、旋转及比例不变性的图像特征的方法,不变矩的主要思想是使用对变换不敏感且基于这些区域的几个矩作为形状特征,从而进行图像识别的方法。不变矩是描述区域的一种方法,由于矩不变量具有不随图像的大小、位置及方向而变化的特点,对于提取图像中形态特征来说,是一个非常有用的工具。Hu利用二阶和三阶的中心矩构造出了七个不变矩,他们在连续的图像条件下可保持平移、缩放和旋转不变,具体定义如下[[[]基于Hu矩和Zernike矩的图像目标识别算法设计。
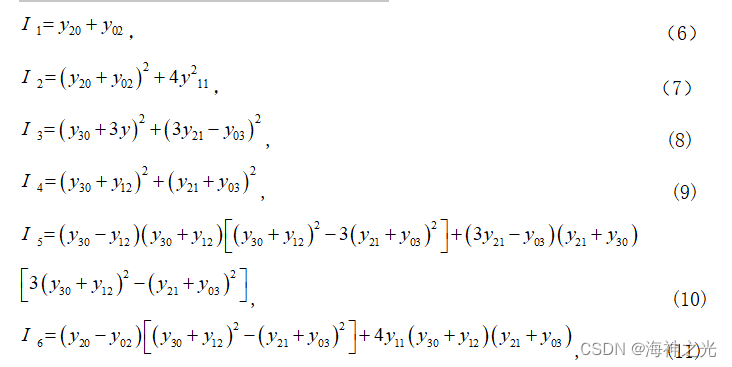
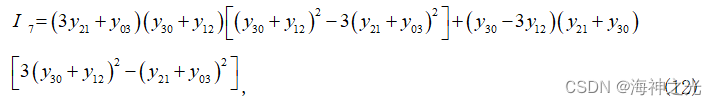
Hu在1962年证明了它们具有旋转、缩放及平移不变性。实际上,在对图片中物体的识别过程中,只有I1和I2不变矩保持的比较好,其他几个不变矩带来的误差相比之下较大。由Hu矩特征组量对图像进行识别,优点是速度快,缺点是识别效率较低。
5 实验结果及分析
5.1 特征提取流程图
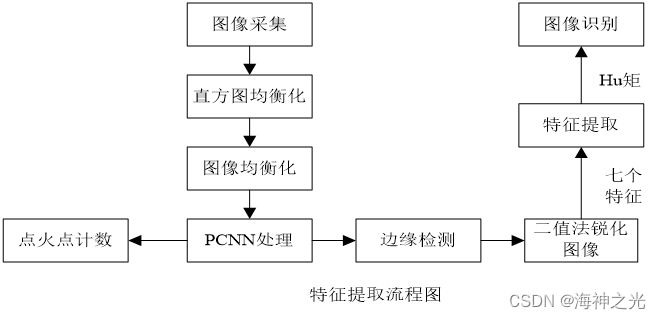
5.2 PCNN处理步骤
步骤1 采集中药材显微图像。
步骤2 对采集到的药材显微图像进行图像均衡化处理。
步骤3 对步骤2处理后的图像进行PCNN处理。
步骤4 对步骤4处理后的图像进行边缘检测及二值法锐化图像。
以下为具体过程:
将采集好的中药材显微图像二值化及PCNN处理,结果如下:
二、部分源代码
function H = PCNNfun(I)
PS=imread('银柴胡.png');
%PS=rgb2gray(PS);
PS=PS(:,:,2);
[m,n]=size(PS); %测量图像尺寸参数
GP=zeros(1,256); %预创建存放灰度出现概率的向量
for k=0:255
GP(k+1)=length(find(PS==k))/(m*n); %计算每级灰度出现的概率,将其存入GP中相应位置
end
%直方图均衡化
S1=zeros(1,256);
for i=1:256
for j=1:i
S1(i)=GP(j)+S1(i); %计算Sk
end
end
S2=round((S1*256)+0.5); %将Sk归到相近级的灰度
%图像均衡化
f=PS;
for i=0:255
f(find(PS==i))=S2(i+1); %将各个像素归一化后的灰度值赋给这个像素
end
三、运行结果

四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社,2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社,2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社,2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社,2015.
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除