首语:
-学了一个多月的机器学习,对于神经网络才刚刚接触,感知机的实现相对好理解,但神经网络的逻辑较为复杂,在这做一个总结和思考。希望能得到各位大佬的指正。
感知机(神经元)
适合做简单的分类或线性方程, 如判断是不是正数, 无法处理复杂的多维特征
实现:参考
关键的感知机的参数优化方法:
wi = w + n(y- y_pre)xi
bi = b + n(y- y_pre)
神经网络的结构
多个神经元组成
正向传播
h = wi xi + bi
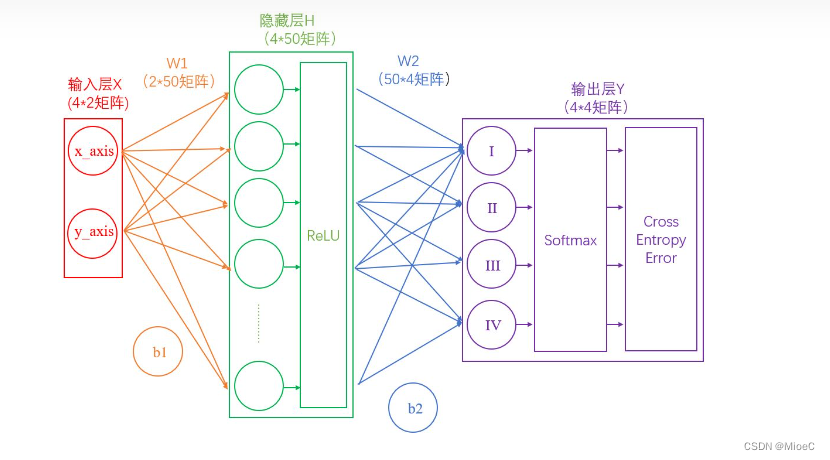
下面进行正向传播的代码实现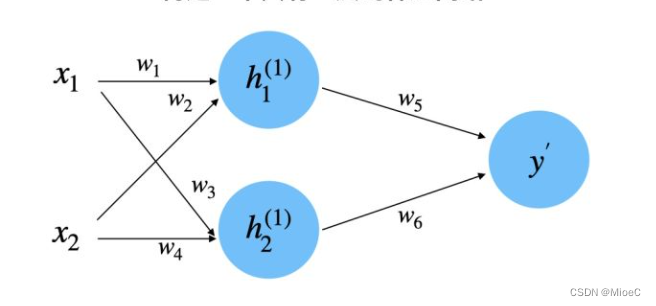
def sigmoid(x):
return 1/(1 + np.exp(-x))
def loss_mse(y_true, y_pred):
return ((y_true - y_pred) ** 2).mean()
def re_sigmoid(x):
fx = sigmoid(x)
return fx * (1 - fx)
class Neural(object):
def feed_forwad(self, x):
h1 = sigmoid(w1 * x[0] + w2 * x[1] + b1)
h2 = sigmoid(w2 * x[0] + w4 * x[1] + b2)
o1 = sigmoid(h1 * w5 + h2 * w6 + b3)
return o1
而反向传播的实现比较复杂,解释下, 我们要计算出Loss 对于所有参数的导数,即每个参数会影响到Loss 的变化大小, 然后不断调整参数大小,达到降低loss 的效果。
比如, 影响到打篮球的属性有身高和速度,我们想设计一个算法, 用来判断每个人的打篮球天赋,
通过导数得到 关于身高的比例为0.7, 速度为0.3, 不断调整参数,使得 准确度达到最高。
我们现在的目的就是求出所有的导数,先列出所有的关系函数
Loss = loss_mes = ((y - y') ** 2).mean() #y 和y '是矩阵形式
# dL/dy' = -2 (y - y')
# 往前推
y' = f(w5 * h1+ w6 * h2 + b3) # f为激活函数 h1, h2 为上个神经节点的输出
# dy'/dw5 = h1 * f'(x)
# dy'/dw6 = h2 * f'(x)
# dy'/db3 = f'(x)
# dL/dw5 = dL/dy' * dy'/dw5
# dL/dw6 = dL/dy' * dy'/dw6
# dL/db3 = dL/dy' * dy'/db3
相同的 可以得出
h1 = f(w1 * x[0] + w2 * x[1] + b1)
h2 = f(w3 * x[0] + w4 * x[1] + b2)
dL/dw1 = dL/dy' * dy'/dh1 * dh1/dw1
dh1/dw1 = x[0] * f'(x)
dh1/dw2 = x[1] * f'(x)
dh1/db1 = * f'(x)
dL/dw2 = dL/dy' * dy'/dh2 * dh2/dw2
dh2/dw3 = x[0] * f'(x)
dh2/dw4 = x[1] * f'(x)
dh1/db2 = * f'(x)
接下来 ,直接进行更新
wi = wi - rate * dwi
w1 -= rate * dl/dw1
.....
完整代码如下:
# 訓練神经网络进行性别的判定
import numpy as np
data = np.array([
[-2, -1], # Alice
[25, 6], # Bob
[17, 4], # Charlie
[-15, -6], # Diana
])
all_y_trues = np.array([
1, # Alice
0, # Bob
0, # Charlie
1, # Diana
])
# 激活函数
def sigmoid(x):
return 1/(1+np.exp(-x))
def deriv_sigmoid(x):
fx = sigmoid(x)
return fx * (1 - fx)
def loss_mse(y_true, y_pred):
# 均方误差 损失函数
return ((y_true - y_pred) ** 2).mean()
class Neural(object):
def __init__(self):
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# 截距项,Biases
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
self.rate = 0.1
def feed_forward(self, x):
# 正向传播, 用于评估 损失函数
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid((self.w5 * h1 + self.w6 * h2 + self.b3))
return o1
def train(self, data, y_labels):
learn_rate = 0.1
epochs = 1000
# 每次训练,将先正向传播,在计算损失函数, 然后反向传播,更新参数, ,在正向传播 目的就是为了降低损失函数的值
for i in range(epochs):
for (x, y_label) in zip(data, y_labels):
#1、正向传播
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
#2、计算损失函数
# 损失函数求导 1/n(y_true - y_pred) ** 2 = 0 + (-1) * 2 * (y_true - y_pred)
dL_j = -2 * (y_label - o1)
#3、 反向传播
#dw1... dw6
#求j 的值
#j = f(w5h1 + w6h2 + b3)
#dj/dw5 = h1 * f' dj/dw6 = h2 * f'
#dL/w5 = dL/j * dj/w5
dl_w5 = dL_j * h1 * deriv_sigmoid(o1)
dl_w6 = dL_j * h2 * deriv_sigmoid(o1)
dl_b3 = dL_j * deriv_sigmoid(o1)
#dl/h1 = dL/dj * dj/dh1 = da_j * w5
dl_h1 = dL_j * self.w5 * deriv_sigmoid(o1)
dl_h2 = dL_j * self.w6 * deriv_sigmoid(o1)
#h1 = f(w1* x1 + w2 * x2 + b1)
#h2 = f(w3 * x1 + w4 * x2 + b2)
#dl/w1 = dl/j * dj/h1 * dh1/dw1
dl_w1 = dL_j * dl_h1 * x[0] * deriv_sigmoid(h1)
dl_w2 = dL_j * dl_h1 * x[1] * deriv_sigmoid(h1)
dl_b1 = dL_j * dl_h1 * deriv_sigmoid(h1)
dl_w3 = dL_j * dl_h2 * x[0] * deriv_sigmoid(h2)
dl_w4 = dL_j * dl_h2 * x[1] * deriv_sigmoid(h2)
dl_b2 = dL_j * dl_h2 * deriv_sigmoid(h2)
#注: 因为b的求导都为1 所以直接更新为rate * b
#4、 更新w, b
self.w1 -= dl_w1 * learn_rate
self.w2 -= dl_w2 * learn_rate
self.w3 -= dl_w3 * learn_rate
self.w4 -= dl_w4 * learn_rate
self.w5 -= dl_w5 * learn_rate
self.w6 -= dl_w6 * learn_rate
self.b1 -= dl_b1 * learn_rate
self.b2 -= dl_b2 * learn_rate
self.b3 -= dl_b3 * learn_rate
if i % 10 == 0:
y_preds = np.apply_along_axis(self.feed_forward, 1, data)
loss = loss_mse(y_labels, y_preds)
print("Epoch %d loss: %.3f" % (i, loss))
# def __str__(self):
# pass
# return 'weights\t:%s\nbias\t:%f\n' % (np.array([self.w1, self.w2, self.w3, self.w4, self.w5, self.w6]), np.array([self.b1, self.b2, self.b3]))
neural = Neural()
neural.train(data, all_y_trues)
print(neural)
emily = np.array([-7, -3]) # 128 pounds, 63 inches
frank = np.array([20, 2]) # 155 pounds, 68 inches
print("Emily: %.3f" % neural.feed_forward(emily)) # 0.951 - F
print("Frank: %.3f" % neural.feed_forward(frank)) # 0.039 - M