深度学习分类网络总结

AlexNet

前言

AlexNet是由Hinton和其学生Alex所设计，获得了2012 ILSVRC（ImageNet Large Scale Visual Recognition Challenge）竞赛的冠军，top5错误率为15.3%，远超第二名的26.2%，证明了卷积神经网络在图像识别任务中的优越性^[1]。

一、网络结构

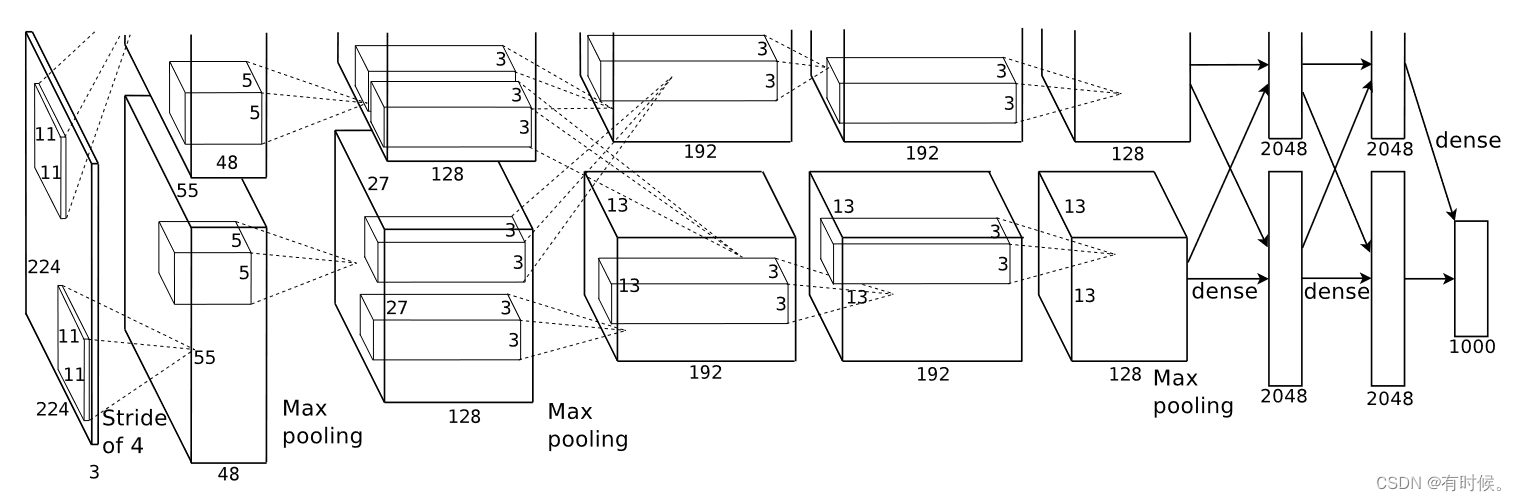
在这里插入图片描述
引用原论文中的网络结构图，可以看出AlexNet共有8层，5个卷积层和3个全连接层。使用torchstat工具打印pytorch官方实现的AlexNet中每层的输入输出尺寸、参数量（parameters）和计算量（FLOPs，MACs）：

import torchvision.models as models
from torchstat import stat

alexnet = models.alexnet()
stat(alexnet, (3,224,224))

# 附Pytorch官方实现的AlexNet结构，与原始论文有所区别
AlexNet(
  (features): Sequential(
    (0): Conv2d(3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2))
    (1): ReLU(inplace=True)
    (2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (3): Conv2d(64, 192, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (4): ReLU(inplace=True)
    (5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (6): Conv2d(192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (7): ReLU(inplace=True)
    (8): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (9): ReLU(inplace=True)
    (10): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (11): ReLU(inplace=True)
    (12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (avgpool): AdaptiveAvgPool2d(output_size=(6, 6))
  (classifier): Sequential(
    (0): Dropout(p=0.5, inplace=False)
    (1): Linear(in_features=9216, out_features=4096, bias=True)
    (2): ReLU(inplace=True)
    (3): Dropout(p=0.5, inplace=False)
    (4): Linear(in_features=4096, out_features=4096, bias=True)
    (5): ReLU(inplace=True)
    (6): Linear(in_features=4096, out_features=1000, bias=True)
  )
)

在这里插入图片描述
简单总结一下输入输出尺寸、参数量和计算量的计算方法：

1. 输入输出尺寸

卷积层和池化层的输出尺寸可根据下式计算： $W_{out}=\frac{W_{in}-K+2P}{S}+1$ 上式中： $W_{in}$ 为输入特征图尺寸，K为卷积核尺寸，P为padding大小， $W_{out}$ 为输出特征图尺寸。
以第一个卷积层为例：输入shape为（3，224，224），卷积核为11×11，步长为4，padding为（2，2），参数代入可得： $W_{out}=\frac{224-11+4}{4}+1=55.25$ 向下取整为55，卷积核数量为64，因此输出shape为（64，55，55）。

2. 参数量

卷积层参数量 = $K*K*C_{in})*C_{out}+C_{out}$ ，全连接层看作K=1的卷积层即可。
以第一个卷积层为例：params = 11×11×3×64+64=23296
以第一个全连接层为例：params = 1×1×9216×4096+4096=37752832

3. 计算量（FLOPs，MACs/MAdd）

FLOPs（Float Point Operations）：浮点运算次数，用来衡量算法或模型的复杂度，每一个加、减、乘、除都算一次浮点运算。
MACs（Multiply-Accumulate Operations）：乘加累积操作次数，一次乘加累积操作包括一个乘法操作和一个加法操作。因此，在数值上通常有FLOPs=2*MACs这种关系。

FLOPs计算方法： 以卷积层为例，假设经过卷积后输出 $C_{out}$ 个尺寸为 $H_{out}×W_{out}$ 的特征图，单个特征图中的每个值都是经过一次卷积计算而得，那么卷积层的总FLOPs= $H_{out}×W_{out}×C_{out}$ × 一次卷积的FLOPs。一次卷积计算可以简化为 $y = w x + b$ ，这里的 $y$ 就是输出特征图中的某个值， $w$ 为 $K×K×C_{in}$ 的权值矩阵， $w x$ 包含 $K×K×C_{in}$ 个乘法操作和 $K×K×C_{in}-1$ 个加法操作， $+ b$ 包含1个加法操作，因此一次卷积的FLOPs= $K×K×C_{in})+(K×K×C_{in}-1)+1=2*K^2*C_{in}$ 。那么卷积层的总FLOPs可按下式计算：
$=H_{out}×W_{out}×C_{out}×2×K^2×C_{in} \approx2×params×H_{out}×W_{out}$ （torchstat中的FLOPs和MAdd貌似反过来了？）

二、亮点

1. ReLU激活函数

作者在论文中提到“对于梯度下降的训练时间，sigmoid和tanh这样的饱和非线性函数比非饱和非线性函数ReLU慢得多”，速度慢的原因是sigmoid和tanh函数中涉及到了指数运算，因此在AlexNet中选择ReLU函数作为激活函数。

# 绘制激活函数图像
import numpy as np
import matplotlib.pyplot as plt

plt.rc('font',family='Times New Roman', size=15)

x = np.linspace(-10,10,500)
sigmoid = 1 / (1+np.exp(-x))
tanh = (np.exp(x)-np.exp(-x)) / (np.exp(x)+np.exp(-x))
relu = np.where(x<0, 0, x)

fig = plt.figure()
ax = fig.add_subplot(211)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.plot(x, sigmoid, label='sigmoid')
plt.plot(x, tanh, label='tanh')
plt.grid(linestyle='-.')
plt.legend()
ax2 = fig.add_subplot(212)
ax2.spines['right'].set_visible(False)
ax2.spines['top'].set_visible(False)
ax2.spines['left'].set_position(('data',0))
ax2.spines['bottom'].set_position(('data',0))
plt.plot(x, relu, label='ReLU')
plt.grid(linestyle='-.')
plt.legend()
plt.tight_layout()
plt.show()

在这里插入图片描述

作者通过实验证明了ReLU函数相比tanh函数的优势：使用ReLU激活函数的四层CNN在CIFAR-10数据集上达到25%错误率的速度比tanh激活函数大约快6倍。(下图中实线为ReLU，虚线为tanh)
除了速度快，ReLU激活函数还能够避免饱和函数所引起的梯度消失问题。

2. GPU并行训练

论文中提到一个GTX 580GPU只有3GB的内存，限制了可以用其进行训练的网络的最大大小，因此将网络拆分到两个GPU上，两个GOU可以直接读取和写入彼此的内存，而不需要经过主机内存，双gpu网络比单gpu网络花费更少的训练时间。作者所采用的并行化方案是将神经元的一半放在单个GPU上，另外还使用了一个技巧：GPU只在特定层中进行通信。

3. 局部响应归一化（LRN）

受神经生物学中“侧抑制”概念（一个被兴奋的神经元能降低周围神经元活性）的启发，作者提出了局部响应归一化，计算方法如下：
在这里插入图片描述
式中：
$b_{x,y}^{i}$ 表示第 $i$ 个特征图在位置 $(x, y)$ 处经过局部响应归一化后的值
$a_{x,y}^{i}$ 表示第 $i$ 个特征图在位置 $(x, y)$ 处经过局部响应归一化前的值
$k,\alpha, \beta$ 为超参数
$N$ 是特征图总数， $n$ 表示取多少个相邻特征图，利用它们在位置 $(x, y)$ 处的值（也就是式中的 $a_{x,y}^{j}$ ）进行求和
Pytorch中的实现方式与原论文中有一处不同，将 $\alpha$ 改为了 $\frac{\alpha}{n}$ ：
在这里插入图片描述

# 测试Pytorch中的LRN层
import torch
import torch.nn as nn
import torch.nn.functional as F

lrn = nn.LocalResponseNorm(size=3, alpha=1, beta=1, k=1) 
input_tensor = F.relu(torch.randn((1,4,3,3))) # (batchsize, C, H, W), 4个size为3*3的特征图
output_tensor = lrn(input_tensor)

# 归一化前
tensor([[[[0.0000, 0.0000, 0.0000],
          [1.5463, 1.2684, 1.5114],
          [0.6285, 1.6448, 0.0000]],

         [[0.5272, 0.0000, 0.3121],
          [0.9505, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000]],

         [[1.1392, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000],
          [0.1394, 0.0000, 0.5774]],

         [[1.0331, 1.0747, 0.0000],
          [1.0267, 0.9921, 0.0000],
          [0.0000, 0.0000, 0.0000]]]])
# 归一化后
tensor([[[[0.0000, 0.0000, 0.0000],
          [0.7370, 0.8256, 0.8580],
          [0.5554, 0.8649, 0.0000]],

         [[0.3457, 0.0000, 0.3023],
          [0.4530, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000]],

         [[0.6056, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000],
          [0.1385, 0.0000, 0.5197]],

         [[0.5777, 0.7760, 0.0000],
          [0.7598, 0.7470, 0.0000],
          [0.0000, 0.0000, 0.0000]]]])

推算一下LRN的计算过程：以第二个特征图在(0,0)位置处的值0.5272为例，求和通道的下限为 $m a x (0, 1 ? 3 / 2)$ =0，上限为 $m i n (4 ? 1, 1 + 3 / 2) = 2$ ，因此考虑0，1，2三个通道，代入公式有：
$b_{0,0}^1 = \frac{0.5272}{1+(0+0.5272^2+1.1392^2)/3}=0.3457$