文章目录
前言
目标检测一直是计算机视觉中最基本的问题之一,它包括目标分类和目标定位两个子任务。 当前最先进的二阶段目标检测器(例如,Cascade R-CNN,MASk R-CNN和Dynamic R-CNN)依赖于边bbox回归(BBR)模块来定位对象;对于单阶段目标检测器(例如,YOLO,SSD)则依靠BBR来定位。
所以说,一个设计良好的损失函数对BBR的成功至关重要。到目前为止,BBR的损失函数主要分为两类:
范数损失函数
通过边框点来计算,比较多得是L1范数,例如:
- SmoothL1 loss
- Dynamic SmoothL1 Loss
- BalanceL1 loss
假定Bbox(x, y, w, h)四个变量是独立的,实际不是,故引入IOU损失
IOU损失函数
通过交并面积计算,例如:
- IOU loss
- GIOU loss(Generalized IOU )
- CIOU loss (Complete IOU)
- DIOU loss(Distance IOU )
- Pixels IOU
- EIOU loss
损失函数怎么来的,由我们需要的性质反推而来,比如我们需要:
-
当回归误差趋近于零时,梯度的大小应该有一个零的极限。
-
在回归误差较小的区域,梯度幅度应迅速增大,在回归误差较大的区域,梯度幅度应逐渐减小。
-
为了灵活地控制低质量实例的抑制程度,需要设置超参数。
-
对于不同的超参数值,梯度函数族应该有一个归一化尺度,例如(0,1),这有助于在高质量和低质量示例之间进行平衡。
IOU loss (2016)
论文:Unitbox: An advanced object detection network
- 优点:
该方法具有非负性、对称性、三角形不等式和尺度不敏感性等优点
- 缺点:
-
如果两个方框没有任何交集,则IOU损失将始终为零,不能正确反映两个方框之间的紧密程度。
-
损失的收敛速度较慢
实现代码:
import numpy as np
def Iou(box1, box2, wh=False):
if wh == False:
xmin1, ymin1, xmax1, ymax1 = box1
xmin2, ymin2, xmax2, ymax2 = box2
else:
xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
# 获取矩形框交集对应的左上角和右下角的坐标(intersection)
xx1 = np.max([xmin1, xmin2])
yy1 = np.max([ymin1, ymin2])
xx2 = np.min([xmax1, xmax2])
yy2 = np.min([ymax1, ymax2])
# 计算两个矩形框面积
area1 = (xmax1-xmin1) * (ymax1-ymin1)
area2 = (xmax2-xmin2) * (ymax2-ymin2)
inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1])) #计算交集面积
iou = inter_area / (area1+area2-inter_area+1e-6) #计算交并比
return iou
GIOU loss (2019)
论文:Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
提出了GIoU的思想。由于IoU是比值的概念,对目标物体的scale是不敏感的。然而检测任务中的BBox的回归损失(MSE loss, l1-smooth loss等)优化和IoU优化不是完全等价的,而且 Ln 范数对物体的scale也比较敏感,IoU无法直接优化没有重叠的部分。
GIOU 损失函数
A,B分别为预测框和目标框,上面公式的意思是:先计算两个框的最小闭包区域面积公式,再计算出IoU,再计算闭包区域中不属于两个框的区域占闭包区域的比重,最后用IoU减去这个比重得到GIoU。
优点:
GIoU有对称区间,取值范围[-1,1]。在两者重合的时候取最大值1,在两者无交集且无限远的时候取最小值-1,因此GIoU是一个非常好的距离度量指标。与IoU只关注重叠区域不同,GIoU不仅关注重叠区域,还关注其他的非重合区域,能更好的反映两者的重合度。
缺点:
- 当|A∩B| = 0时,GIOU loss趋向增C的面积,使其与目标框重叠,这与减小空间位置差异的直觉相反。黑色代表锚盒,蓝色表示目标框。
- 当|A∩B| > 0时,|C?A∪B|的面积总是一个小数字或等于零(当A包含B时,这一项为零,反之亦然)。在这种情况下,GIOU损失降级为IOU损失。因此,GIOU损失的收敛速度仍然慢。
实现函数:
def Giou(rec1,rec2):
#分别是第一个矩形左右上下的坐标
x1,x2,y1,y2 = rec1
x3,x4,y3,y4 = rec2
iou = Iou(rec1,rec2)
area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
area_1 = (x2-x1)*(y1-y2)
area_2 = (x4-x3)*(y3-y4)
sum_area = area_1 + area_2
w1 = x2 - x1 #第一个矩形的宽
w2 = x4 - x3 #第二个矩形的宽
h1 = y1 - y2
h2 = y3 - y4
W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4) #交叉部分的宽
H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4) #交叉部分的高
Area = W*H #交叉的面积
add_area = sum_area - Area #两矩形并集的面积
end_area = (area_C - add_area)/area_C #闭包区域中不属于两个框的区域占闭包区域的比重
giou = iou - end_area
return giou
DIOU loss (2020)
论文:https://arxiv.org/pdf/1911.08287.pdf
DIoU要比GIou更加符合目标框回归的机制,将目标与anchor之间的距离,重叠率以及尺度都考虑进去,使得目标框回归变得更加稳定,不会像IoU和GIoU一样出现训练过程中发散等问题。
优点:
DIoU loss可以直接最小化两个目标框的距离,因此比GIoU loss收敛快得多
对于包含两个框在水平方向和垂直方向上这种情况,DIoU损失可以使回归非常快,而GIoU损失几乎退化为IoU损失。
DIoU还可以替换普通的IoU评价策略,应用于NMS中,使得NMS得到的结果更加合理和有效。
实现代码:
def Diou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
dious = torch.zeros((rows, cols))
if rows * cols == 0:#
return dious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
dious = torch.zeros((cols, rows))
exchange = True
# #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1+area2-inter_area
dious = inter_area / union - (inter_diag) / outer_diag
dious = torch.clamp(dious,min=-1.0,max = 1.0)
if exchange:
dious = dious.T
return dious
CIOU loss (2020)
论文:https://arxiv.org/pdf/1911.08287.pdf
CIOU loss考虑了三个重要的几何因素,即重叠面积、中心点距离和高宽比。给定一个预测框B和一个目标框Bgt, CIOU损失定义如下。
DIoU中对anchor框和目标框之间的归一化距离进行了建模
与以前的损失函数相比,CIOU损失有了显著的改善。 由于v只反映了纵横比的差异,CIOU损失可能会以不合理的方式优化相似性, 这里,CIOU损失确实增加了宽高比的相似度,但它阻碍了模型有效降低(w, h)和(wgt, hgt)之间的真实差异。
实现代码:
def bbox_overlaps_ciou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
cious = torch.zeros((rows, cols))
if rows * cols == 0:
return cious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
cious = torch.zeros((cols, rows))
exchange = True
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1+area2-inter_area
u = (inter_diag) / outer_diag
iou = inter_area / union
with torch.no_grad():
arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
S = 1 - iou
alpha = v / (S + v)
w_temp = 2 * w1
ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
cious = iou - (u + alpha * ar)
cious = torch.clamp(cious,min=-1.0,max = 1.0)
if exchange:
cious = cious.T
return cious
EIOU loss (2021)
论文:Focal and Efficient IOU Loss for Accurate Bounding Box Regression
针对以上问题,对CIOU损失进行了修正,提出了一种更有效的损失形式。
[公式] 和 [公式] 指覆盖两个盒子的最小的封闭盒子的宽度和高度,其他变量参考以上说明,将损失函数分为三部分:IOU损失、距离损失、方向损失。 这样,就可以保留CIOU loss特征。同时,EIOU loss 直接使目标框与锚框的宽度和高度之差最小,使得收敛速度更快,定位效果更好。
Fcoal-EIOU loss (2021)
论文:Focal and Efficient IOU Loss for Accurate Bounding Box Regression
在BBR中,也存在训练样本不平衡的问题(one-stage检测比较突出),即由于图像中目标对象的稀疏性,回归误差小的高质量样本(锚框)的数量远远少于低质量样本(离群值)。最近的研究表明,异常值会产生过大的梯度,这对训练过程有害。 因此,让高质量的样本为网络训练过程贡献更多的梯度是至关重要的。所以引入Focal loss的提出起到很大作用,因此改进的EIOU loss( Fcoal-EIOU loss ),如下:
Fcoal-EIOU 损失函数
其中IOU = |A∩B|/|A∪B|,γ为控制异常值抑制程度的参数。
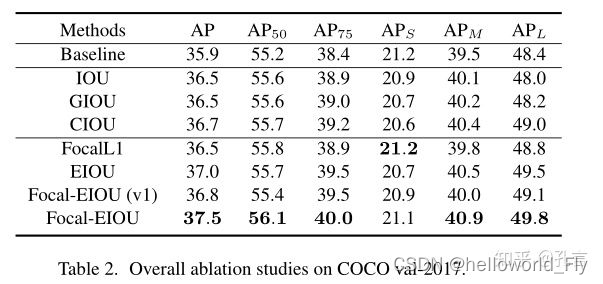
结果对比
以上损失函数性能对比: