[人工智能]使用GNN求解组合优化问题

最近刷到一篇文章，使用图神经网络解决组合优化问题，把组合优化问题抽象为图上的最大割、最大独立集等QUBO问题，用图神经网络求解器求解。感觉这个方法挺有意思，也比较泛用，因此试着跑了一下它的源码，又试了一个简单的区间调度问题，在此记录一下。

论文：Combinatorial Optimization with Physics-Inspired Graph Neural Networks
地址：https://arxiv.org/abs/2107.01188
源码：https://github.com/amazon-research/co-with-gnns-example

1 论文内容

对该领域了解不多，建议参考其他推送或论文原文：
Nat. Mach. Intell.：图神经网络(GNN)，组合优化
亚马逊团队使用受物理启发的图神经网络，解决组合优化等问题
…

1.1 先验知识

组合优化问题：同时面对许多决策，每一个决策只有yes/no两种取值，视为一个0-1变量。那么解空间就是全部0-1变量的所有组合。每种不同的决策组合都会得到一个目标函数值（例如成本或收益），这个目标函数就是优化的对象。

组合优化问题的两个相关例子是最大割与最大独立集。给定一个图，这两个问题可以简单理解为对每个节点进行一次二分类：

最大割：把这个图的节点分为两堆，使得这两堆节点之间的边数最多。两堆节点的标签分别是0和1。
最大独立集(Maximal Independent Set, MIS)：在这个图中找出尽可能多的节点，使得这些节点之间互相没有边相连。找出的节点标签为1，其余为0。

最大割与最大独立集问题的目标函数可以在QUBO（二次无约束二进制优化）框架下写出，在论文第3部分有说明，这篇文章展示了一个实际的例子：定义问题以及用QUBO表示约束。优化对应的目标函数，就能得到一个图的最大割与最大独立集。

度：一个节点的度就是该节点邻边的数量，平均度就是把图中所有节点的度求均值。

图神经网络GNN：图神经网络希望解决的基本任务例如：利用图的信息，进行节点或边的分类、节点或边的特征预测等。训练与预测的基本框架等与其他神经网络没有区别，只是处理的数据结构不同。

图神经网络的一般输入是一个图，它由节点集、边集、邻接矩阵等基本特征组成。对于节点集中的每一个节点，都可以用一个固定形状的张量来表示其特征，用邻接矩阵表征节点之间的关系，最简单的图神经网络认为边只代表邻接关系而没有节点那样的高维特征。

具体到数学形式上，一般的图神经网络输入表示为两个张量：节点集：一个形状为[节点数量，节点特征长度]的2维张量；邻接矩阵：一个形状为[节点数量，节点数量]的2维0-1张量（如果边有权重那就不是0-1值而是具体的权重）。

例如，在一个交通网络中，可以将每条道路视作一个节点。每条道路均拥有车道数、平均流量、平均速度三个属性，可以用一个固定长度为3的1维张量表示，这就是每个节点的特征。若两条道路在十字路口等地方相接，则为这两个节点间添加一条边，用邻接矩阵表示整个路网上道路的邻接情况。这样，这一交通网络的基本特征就可以用一个图来进行表示并送入图神经网络。

图神经网络的输出也可以看作是一个图。例如节点分类问题中，输入一个图，输出一个图，不同的是输出的图的特征张量变成了类别标签，也就是一个one-hot向量。

图神经网络中间的运算可以看作相邻节点信息聚合的过程，通过不断地将邻接节点的信息提取、融合，得到每个节点信息的重新表达，例如类别。

一般来讲，神经网络训练的框架大致如下：输入数据（在这里是图）->通过神经网络计算预测值（也就是网络输出）->计算loss函数（优化的目标，一般是预测值与真实值的差距）->计算神经网络所有参数对loss值的梯度->按照梯度的大小进行梯度下降（一般希望loss尽可能小，若希望尽可能大就是梯度上升），更新神经网络参数。

随着训练的进行，loss函数会变得越来越小，相应的梯度也会减小，参数更新的幅度减小，最后收敛。最理想的情况下，对于一个训练好的神经网络，将数据输入，输出的预测值与真实值完全一致，loss是0，不过一般来说会面临过拟合或数据分布不一等问题，这里不展开。分类问题可以看作是预测类别标签。

1.2 论文方法

这篇论文大概干了这样一件事：把组合优化问题转化为图上的最大割或者最大独立集等QUBO问题，进一步转化为一个图节点二分类问题。然后用图神经网络处理节点间的邻接信息，把QUBO的目标函数松弛，用连续的分类概率代替离散的0-1变量，作为神经网络的loss函数，训练这个图神经网络（输出节点类别概率）。最后用阈值分割得到每个节点/变量的0-1值。

大致流程如论文插图所示：

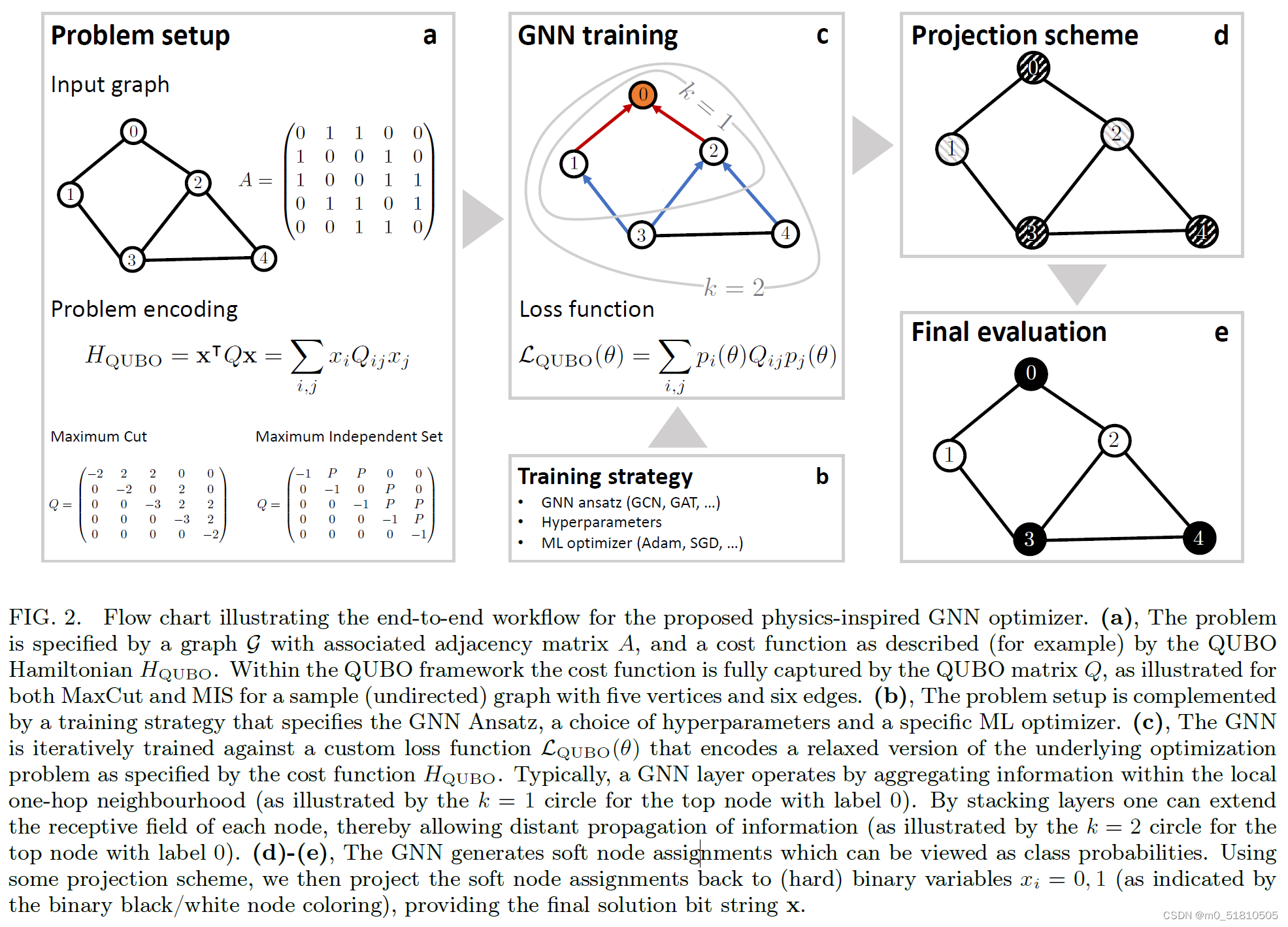
1.2.1 大致原理

将组合优化问题的每一个变量，视作一个图上的一个节点，若两个变量存在某种关系，则将两个节点用一条无向边连接。这样一来，组合优化问题就可以表示为一个图，看作是一个图上的二分类问题，目标是将图的节点分为0-1两类。更具体的，这篇文章提到的例子都转化为最大割或者最大独立集问题，或者其加权或带约束的形式。

这个图上的二分类问题使用图神经网络GNN解决。由于这个图的节点没有特征，只有一个节点的序号，因此首先为要为图的每个节点随机初始化一个张量作为特征，再将图输入神经网络。神经网络的输出是每个节点类别的概率。

这个二分类问题的loss函数，设置为松弛的哈密顿量，也就是前面说的用QUBO表示的那个目标函数。用神经网络的输出的每个节点的类别概率（在0-1之间的浮点数）代替0-1变量，用同样的方法计算哈密顿量，得到loss值，然后进行梯度下降训练神经网络。松弛是为了让目标函数连续化，可导（否则求不了梯度）。

如上图所示，原来的组合优化问题目标函数是$H_{QUBO}=X^{T}QX$，其中的$X$是所有变量/节点取值按顺序排列的0-1组合，例如$[0,1,0,0,...,1{]}^T$这样的一个矩阵。而$Q$是对应问题的QUBO矩阵，该矩阵如何写出参考前面的内容，上图a部分给出了最大割与最大独立集对应的$Q$矩阵形式。

松弛后的目标函数变为${\mathcal{L}}_{QUBO}=P(\theta {)}^{T}QP(\theta )$，其中$P(\theta )$是神经网络的输出，是一个被sigmoid函数压缩到0-1之间的浮点值，例如$[0.1,0.9,0.5,...,0.8{]}^T$这样一个值。

最终，当目标函数收敛的之后，拿到神经网络的输出$P(\theta )$，按照阈值选择节点的类别。在源码中，该参数是PROB_THRESHOLD=0.5。

1.2.2 源码关键实现

在代码实现上，该论文使用了基于pytorch后端的dgl库，使用dgl.nn.pytorch.conv.GraphConv(in_feats, out_feats, norm='both', weight=True, bias=True, activation=None, allow_zero_in_degree=False)（官方文档）实现了一个简单的两层图卷积，用来解决最大独立集的问题。其他的问题并未包含其中，在其他问题中使用需要在gen_q_dict_mis()函数中定义具体问题的Q矩阵。

初始化图节点张量的方法在源码./utils.py的get_gnn()函数中，使用nn.Embedding(n_nodes, dim_embedding)初始化了一个查词表，作为1.1中提到的节点集（形状[节点数量，节点特征长度]）作为输入。

从源码来看，神经网络的输出的图卷积层定义如下：self.conv2 = GraphConv(hidden_size, number_classes).to(device)，而相应的参数被设置为'number_classes': 1，最后输出时用h = torch.sigmoid(h)过了一层sigmoid。这说明神经网络输出的$P(\theta )$维度是与原0-1变量$X$一致的，在0-1之间的浮点值。

在loss_func(probs, Q_mat)这一函数中，直接看到该loss的求法是cost = (probs_.T @ Q_mat @ probs_).squeeze()，这与1.2.1是一致的。源码的probs或probs_变量就是1.2.1的神经网络的输出$P(\theta )$，也就是源码中的probs = net(dgl_graph, inputs)[:, 0]。

个人感觉这篇文章有意思的地方在于：这番操作简洁的有点反直觉，甚至有点艺术，然而效果很好，甚至达到sota。它把一个离散的目标函数简单地松弛为连续量，作为loss函数拿神经网络简单训练一下，就能求解离散的组合优化问题，甚至是一个NP难问题。同时，它泛用性很强，一次性的将图上的组合优化问题统一在二分类的框架下，一并解决了，并且能用于许多现实问题。除此之外，这一方法能够求解百万级别变量的大规模问题，而其他方法有些困难。最后，这个方法跨越几个领域，其QUBO的操作和量子退火算法有些关系（毕竟论文标题就是物理启发的图神经网络组合优化），能在量子退火上处理的问题应该也能用这个方法处理。另外涉及到了运筹优化、图论、机器学习等领域的一些知识。

1.3 实际问题上的应用

前面的部分比较抽象，这一部分就举几个简单的例子演示一下这个组合优化求解器在实际问题中的应用。这一部分对应论文第六部分APPLICATION IN INDUSTRY，更具体的内容（如目标函数）可以直接阅读原文及对应参考文献。应用的方法就是将实际问题转化为一个图上的问题，用这个GNN求解器求解图的最大割或最大独立集等QUBO问题。

1.3.1 风险分散

面对大量的投资项目，风险分散是很有必要的。两个项目的关联越紧密，其面对的风险就越一致。为了分散风险，我们希望找到这些项目中关联性最小的一批项目来进行投资，每个项目的投资只有是或否两种状态。

这可以转化为一个图上的最大独立集问题。我们将每一个投资项目视为一个节点，如果两个投资项目比较相关，那么把它们用一条边相连。由于图的最大独立集的节点之间没有边相连，那么最大独立集节点所代表的项目之间关联就最不紧密。

这样，将项目构建的图送进该论文的GNN求解器，用它求最大独立集，就可以得到可以投资的项目组合。

1.3.2 Interval Scheduling（不大懂译，区间调度？）

考虑如下场景：只有一台机器，但是有多个任务需要执行，每个任务有确定的起点与终点时间，在每个任务执行的期间不能做其他的事情。最多能够完成几个任务呢？（是任务个数而不是总工作量）

这个问题可以转化为一个求最大独立集的问题。把每个任务视作一个节点，如果两个任务间存在冲突（即两个任务持续的时间区间存在重合），那么就将两个任务用一条边相连。这样，任务间的互相冲突可以表达为一个图。这个图上的最大独立集所代表的任务，就是最多能够完成的任务集，因为这些节点互相之间没有边相连，所代表的任务也不存在冲突。

把这一冲突关系图送入求解器，求最大独立集，就可以解决问题。

如果希望总工作量最大，那就是一个加权的最大独立集问题，同样能够用QUBO表示，并松弛后用该求解器求解。

1.3.3 配水管网的传感器布置

我们希望检测网络中每一个水管的状态，同时放置最少的压力传感器以覆盖所有水管。在储罐处或水管连接处放置传感器能够同时检测所有相邻水管的状态。

我们将水管连接处视作节点，将水管视作边，用图表示整个配水管网。我们需要解决的就是一个带约束与加权的最小割问题，约束可以用一个合适的惩罚值实现，参考二次无约束二值优化模型（The Quadratic Unconstrained Binary Optimization(QUBO) model）。详见参考文献112：Solving Sensor Placement Problems In Real Water Distribution Networks Using Adiabatic Quantum Computation。这个问题可以被表示为QUBO问题，进而松弛作为loss函数，将配水管网送进该GNN求解器求解。

2 论文求解器源码的使用

源码比较简单，而且注释等写的很详细，值得学习。相关代码只有./utils.py和./gnn_example.ipynb两个文件。./utils.py中是一些依赖的具体的方法，内容包括图神经网络的定义class GCN_dev(nn.Module)、用以测试的随机图的生成generate_graph()、损失函数的构建（这里只有MIS最大独立集的）loss_func(probs, Q_mat)、神经网络的训练逻辑（也就是该求解器的求解过程）run_gnn_training()。./gnn_example.ipynb是运行的主文件，包括超参数的设置，用图神经网络求解器、networkx自带的图求解器，分别求解MIS问题等。.ipynb文件需要在jupyter notebook中运行，如果想在其他IDE中运行，在jupyter notebook打开后可以将其导出为.py文件，参考JupyterLab中如何导出py格式文件。

跑示例代码，只需要将官方源码下载解压，并按照./requirements.txt安装所有依赖库，直接运行./gnn_example.ipynb即可。

2.1 安装依赖库

2.1.1 法1:使用requirements.txt

requirements.txt是几乎每个深度学习仓库中都会存在的内容，里面写明了该仓库的依赖库及其版本，直接利用该文件可以快速配置仓库的运行环境。在这一官方源码中也存在。下面的内容在win10下进行，其他操作系统流程应该差不多。

1、首先下载项目文件https://github.com/amazon-research/co-with-gnns-example，并解压到文件夹中。
使用anaconda来管理虚拟环境，官方库提供以下命令来安装依赖库：

conda create -n <environment_name> python=3.8 --file requirements.txt -c conda-forge -c dglteam -c pytorch

2、安装anaconda并设置环境变量，参考该文章Anaconda安装（过程详细）。
3、安装好之后，打开anaconda prompt，并cd到项目文件夹，也就是requirements.txt所在文件夹下，打开参考打开anaconda prompt的操作步骤，cd参考anaconda prompt中cd到指定目录。

上面那行命令的<environment_name>意味着该处需要填写一个变量名，随便设置一个名字就行。例如下面这样：

conda create -n pytorch python=3.8 --file requirements.txt -c conda-forge -c dglteam -c pytorch

4、直接在刚刚cd好的anaconda prompt中运行该命令即可创建一个虚拟环境并安装依赖库。

5、运行该虚拟环境的jupyter notebook（在requirement.txt里面一并安装了），然后导入该项目，直接运行./gnn_example.ipynb即可，需要注意路径需要在项目文件夹下。

2.1.2 法2:单独安装缺少的依赖库

由于我已经有了一套pytorch的虚拟环境，因此只需要单独安装一部分依赖库即可。但是如果所安装库与python版本和requirement.txt不对应，可能会产生一些bug，这是由于一些库版本不同，相同功能的接口可能改变或者取消。需要找到新版本中对应的功能，稍微改变一下源码才能跑。

1、安装pytorch：pytorch是依赖的深度学习库，进入pytorch官方网站，选择cuda版本进行conda安装，cuda版本的选择与gpu的驱动、pytorch的版本支持有关。需要注意的是，不需要像前几年那样在电脑上配置任何cuda、cudnn软件，只需要安装conda命令下的cudatoolkit这个库即可，安装tensorflow也是如此。

2、安装dgl：dgl是基于pytorch等库实现的图神经网络库，进入dgl官方网站，同样像上述pytorch那样安装即可。

3、安装networkx：networkx是用以处理图结构的python库，直接conda install networkx。

安装完后，同样在ide中直接运行./gnn_example.ipynb即可。

在运行时，我出现了如下问题：ModuleNotFoundError: No module named 'networkx.algorithms.approximation.independent_set'，这是由networkx版本不对应导致的，independent_set这个模块用来求图的一个独立集，只影响到源码第6步，图神经网络求解器还是能够正常使用的。requirements.txt中的networkx库版本是2.5，而我直接安装的版本是2.7.1，在2.7.1中这一方法的接口改变了，参考networkx官方文档。

解决的方法是：把./gnn_example.ipynb中的该行代码（上面那行），换成下面一行：

from networkx.algorithms.approximation.independent_set import maximum_independent_set as mis #2.7.1找不到该库，仅影响第6步
from networkx.algorithms.mis import maximal_independent_set as mis #2.7的写法，上面那个是2.5

官方的requirements.txt与我使用的库的版本如下，我使用的gpu是3060：

./co-with-gnns-example/requirements.txt内容：
# -c dglteam
dgl==0.5.3
# -c pytorch
pytorch==1.7.1
# -c conda-forge
numpy==1.19.5
networkx==2.5
jupyter==1.0.0
requests==2.25.1
matplotlib==3.3.2

我的虚拟环境库版本：
dgl-cuda11.1              0.8.2
torch                     1.8.1+cu111
numpy                     1.22.3
networkx                  2.7.1
matplotlib                3.2.2
python                    3.8.8
cudatoolkit               11.1.1

2.2 运行示例代码

当配置好虚拟环境后，在ide中打开./gnn_example.ipynb，并按需要对库接口做上述修改后，直接运行即可。注意ide里的路径需要是项目文件夹./co-with-gnns-example/，这是由于./gnn_example.ipynb中调用了同目录下的./utils.py文件的函数，若路径不对是找不到它的。

示例代码产生一个随机图，演示了一下该论文求解器求解该随机图最大独立集（MIS）问题的方法，其他如求最大割的内容并未涉及到。

生成随机图的函数是generate_graph()，直接在./utils.py下找到该方法，有详细的说明。示例的参数是n=100，d=3，graph_type=‘reg’，这意味着生成一个随机图，有100节点，度为3。这个接口还实现了多种类型的图生成方法。

对于用该函数生成的随机图nx_graph，该文件中用该论文的GNN求解器、networkx库的maximal_independent_set()方法分别求解并比较了结果，做了一个简单的可视化。直接运行结果如下：

runfile('C:/Users/Administrator/Desktop/co-with-gnns-example-main/gnn_example.py', wdir='C:/Users/Administrator/Desktop/co-with-gnns-example-main')
Will use device: cuda, torch dtype: torch.float32
Generating d-regular graph with n=100, d=3, seed=1
Running GNN...
Epoch: 0, Loss: 44.14915466308594
Epoch: 1000, Loss: 16.639339447021484
Epoch: 2000, Loss: 4.808122634887695
Epoch: 3000, Loss: 1.1103489398956299
Epoch: 4000, Loss: -0.938180685043335
Epoch: 5000, Loss: -3.6288394927978516
Epoch: 6000, Loss: -11.529044151306152
Epoch: 7000, Loss: -21.938472747802734
Epoch: 8000, Loss: -31.172693252563477
Epoch: 9000, Loss: -36.286048889160156
Epoch: 10000, Loss: -39.039188385009766
Epoch: 11000, Loss: -40.35068893432617
Epoch: 12000, Loss: -40.703224182128906
Epoch: 13000, Loss: -40.85045623779297
Epoch: 14000, Loss: -40.92048645019531
Stopping early on epoch 14816 (patience: 100)
GNN training (n=100) took 61.955
GNN final continuous loss: -40.95294952392578
GNN best continuous loss: -40.95294952392578
Calculating violations...
Independence number found by GNN is 41 with 0 violations
Took 61.97s, model training took 61.956s
Running built-in MIS solver (n=100).
Calculating violations...
Independence number found by nx solver is 39 with 0 violations.
MIS solver took 0.001s

输出的解释如下：示例代码用d-regular方法生成了一个随机图，参数是n=100, d=3, seed=1，代表100节点，平均度3。共训练了14816轮，patience=100意味着最后100轮loss没有提升，达到耐心上限早停（提前停止）了，这一部分见./utils.py下的run_gnn_training()函数。最佳的loss值是-40.95294952392578，也就是MIS问题松弛的QUBO目标函数的最好解。GNN找到的独立集节点数是41个，违背最大独立集限制条件的节点数为0。使用networkx的MIS求解器求解得到的独立集节点数是39个，违背最大独立集限制条件的节点数为0。

从结果来看，GNN求解器求解得到的最大独立集结果，好于networkx的MIS求解器求解得到的最大独立集。

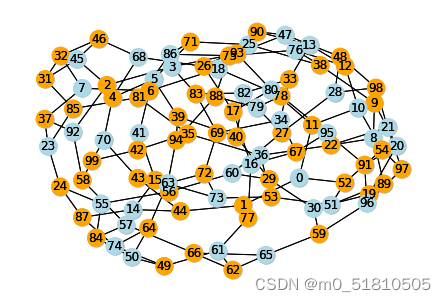
输出图片如下，根据color_map = ['orange' if (best_bitstring[node]==0) else 'lightblue' for node in nx_graph.nodes]这行代码可以得知，蓝色的节点是最大独立集节点，而橙色的是非最大独立集节点：

3 尝试一个区间调度问题

在1.3.2中，我们提到了该求解器能够解决区间调度问题，下面来仔细分析一下这个问题，并看看这个求解器的示例代码如何运用在自己的区间调度问题上。

3.1 区间调度问题如何表示为最大独立集

A Unified Approach to Approximating Resource Allocation and…这篇文章的第10页ppt展示了一个具体的区间调度问题，并展示如何将其表示为最大独立集。我将该页的问题扒下来，尝试了一下GNN求解器的使用。

我们需要解决的问题是：如果只有一台机器，这台机器每一时刻只能做一个任务，且在正在执行的任务结束前不能去做其他任务。现在有多个任务，每个任务有固定的起止时间与持续区间，最多能够完成多少个任务？

任务分布情况的可视化如下：

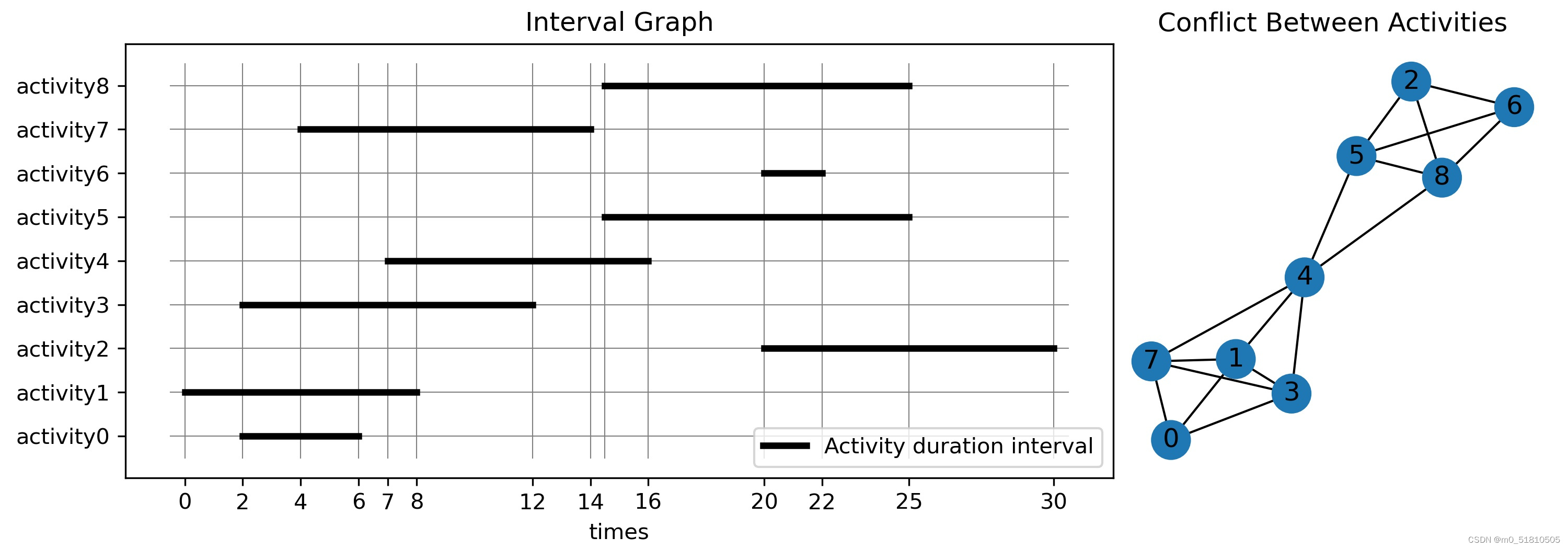
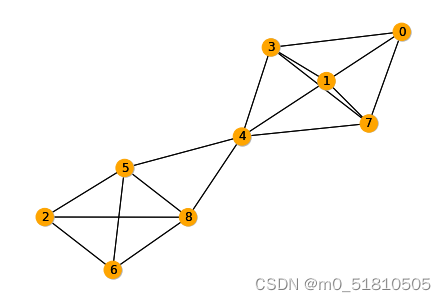
左图是第10页ppt的区间图，横轴代表时间的变化，而纵轴代表9个任务，每个任务有固定的开始与结束区间，每个任务持续的时间区间用粗黑线画出。

如果每一时刻只能做一个任务，那么部分任务在持续的时间区间上存在重合与冲突，例如任务0与任务1、3、7存在冲突，任务0就不能与任务1、3、7一起被选中执行。在右图便使用一个冲突关系图来表明了任务之间的互相冲突。我们将每个任务视为一个节点，如果两个任务在时间上冲突，那么就用一条边将两个节点连接起来。因此可以看到右图上，节点0只与节点 1、3、7相连接，而与其他节点之间不存在边。

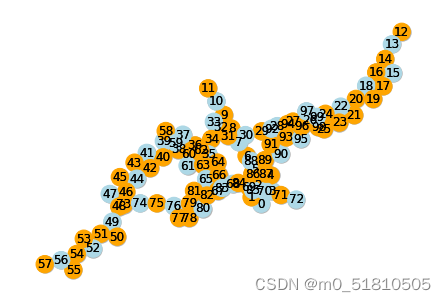
那么我们能够完成任务的最大数量，就是右图的最大独立集数量。右图的最大独立集所代表的任务之间，彼此不存在冲突关系，都可以同时做。并且根据最大独立集的定义，这样选择出的节点数目，或者说任务数，是在这一约束下最好的选择。可视化如下：

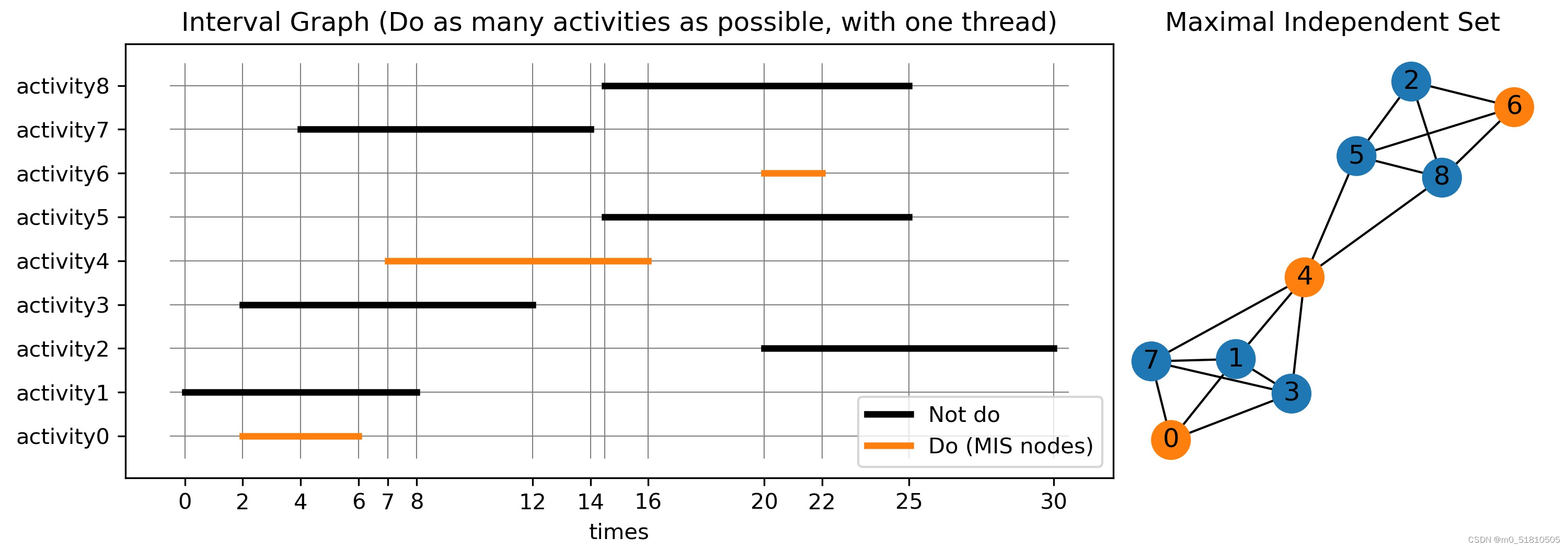
可以看到，右图的最大独立集用橙色标出，是0、4、6。相应的，任务0、4、6就是最终选择去做的任务，也就是该区间调度问题的解。因此最多能做的任务数是3个。

3.2 区间调度问题下GNN求解器的使用

示例源码的GNN求解器正好是解决最大独立集问题的，这与区间调度问题抽象为图问题后是一致的。源码的使用非常简单，只需要将区间调度的冲突关系图保存，并在求解器中读取这张图，代替随机生成的图作为图神经网络的输入，然后改几个参数，即可求解这个冲突关系图的最大独立集。

首先根据区间调度问题的冲突关系生成并保存图：

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from networkx.algorithms.mis import maximal_independent_set as mis

aclist = np.arange(9)
activities = np.array([[1,3], [0,5], [10,13], [1,6], [4,9], [8,12], [10,11], [2,7], [8,12]])
times = np.array([0,2,4,6,7,8,12,14,14.5,16,20,22,25,30])

def conflict(act12):
    # conflict if max(act1.start, act2.start)<min(act1.end, act2.end)
    return True if act12.max(axis=0)[0]<act12.min(axis=0)[1] else False

# 遍历检测冲突，有冲突则构建一条边
edgelist=[]
for i in range(aclist.shape[0]):
    for j in range(i+1,aclist.shape[0]):
        if conflict(activities[[i,j]]):
            edgelist.append((aclist[i], aclist[j]))

# 建冲突关系图 https://www.osgeo.cn/networkx/tutorial.html
G = nx.OrderedGraph() #参考源码，用该函数建图
G.add_nodes_from(aclist)
G.add_edges_from(edgelist)

print(f'nodes:{G.nodes}\nedges:{G.edges}\nadj:{G.adj}\ndegree:{G.degree}')
print(f'mis(maximal_independent_set) nodes:{mis(G)}') #[0, 6|2, 4], 贪心找的，不是最优解，要多跑几次
nx.draw(G, with_labels=True)

nx.write_gpickle(G,'IntervalGraph.gpickle') #保存图

需要注意的是：节点标签必须是[0,1,2,…,8]这样的从0开始的整数，因为源码中直接用节点标签做切片，不这样设置节点标签会报错。

同时这里也用networkx2.7自带的最大独立集方法求解了一下该图的最大独立集，但是基本都只能找到2个，只有少数的机会能找到全部3个。这是由于自带的方法是随机贪心搜索的，实质上只能给出一个还不错的独立集，而不能解决最大独立集问题。所以前面的示例源码中，这一方法只找到39个，而GNN求解器能找到41个。

接着回到./gnn_example.ipynb中，在代码块In [6]找到随机生成图的一行：

# Constructs a random d-regular or p-probabilistic graph
nx_graph = generate_graph(n=n, d=d, p=p, graph_type=graph_type, random_seed=seed_value)

把这行改为加载刚刚自己构建的冲突关系图，以代替随机生成的测试图，注意路径要改为自己的路径：

nx_graph = nx.read_gpickle('./interval graph/IntervalGraph.gpickle')

接下来找到In [5]中# Problem size (e.g. graph size)下定义问题规模的超参数n = 100，将其修改为n = 9，这是由于刚刚的图有9个节点，原来随机生成的图是100个。需要注意的是在这上面还有一个n = 100，那个n被这个覆盖掉了，因此没用了。再次直接运行./gnn_example.ipynb即可。

不过这次，GNN求解器寄了。它并没有像之前那样找到这张图的一个最大独立集，输出的结果如下：

Epoch: 31000, Loss: 0.09334098547697067
Stopping early on epoch 31647 (patience: 100)
GNN training (n=9) took 127.82
GNN final continuous loss: 0.08423598855733871
GNN best continuous loss: 0.0
Calculating violations...
Independence number found by GNN is 0.0 with 0 violations
Took 127.822s, model training took 127.82s
Running built-in MIS solver (n=9).
Calculating violations...
Independence number found by nx solver is 2 with 0 violations.
MIS solver took 0.0s

显然，GNN求解器跑了30000多个epoch，但是没能找到任何一个图上的最大独立集，反倒networkx自带mis求解器找到2个，这是怎么回事呢？

3.3 尝试一个更大规模的区间调度

我首先猜测是因为问题规模太小，因为不论从论文实验部分还是示例源码来说，GNN求解器跑的图节点数都是100起步。因此我用泊松分布生成了一个100个任务的区间调度问题，如下：

np.random.seed(9527)
aclist = np.arange(100)
bias = np.random.poisson(lam=5,size=[100,1])+1
activities = 3*np.arange(100).reshape(-1,1)+np.column_stack((-1*bias,bias))+25
# 查看图的基本属性，如下：
# mis(maximal_independent_set) nodes:[65, 44, 87, 53, 79, 34, 73, 60, 90, 0, 39, 96, 69, 9, 48, 82, 19, 27, 5, 29, 24, 15, 84, 76]
# num of coflicts(edges):325
# average degree:6.5

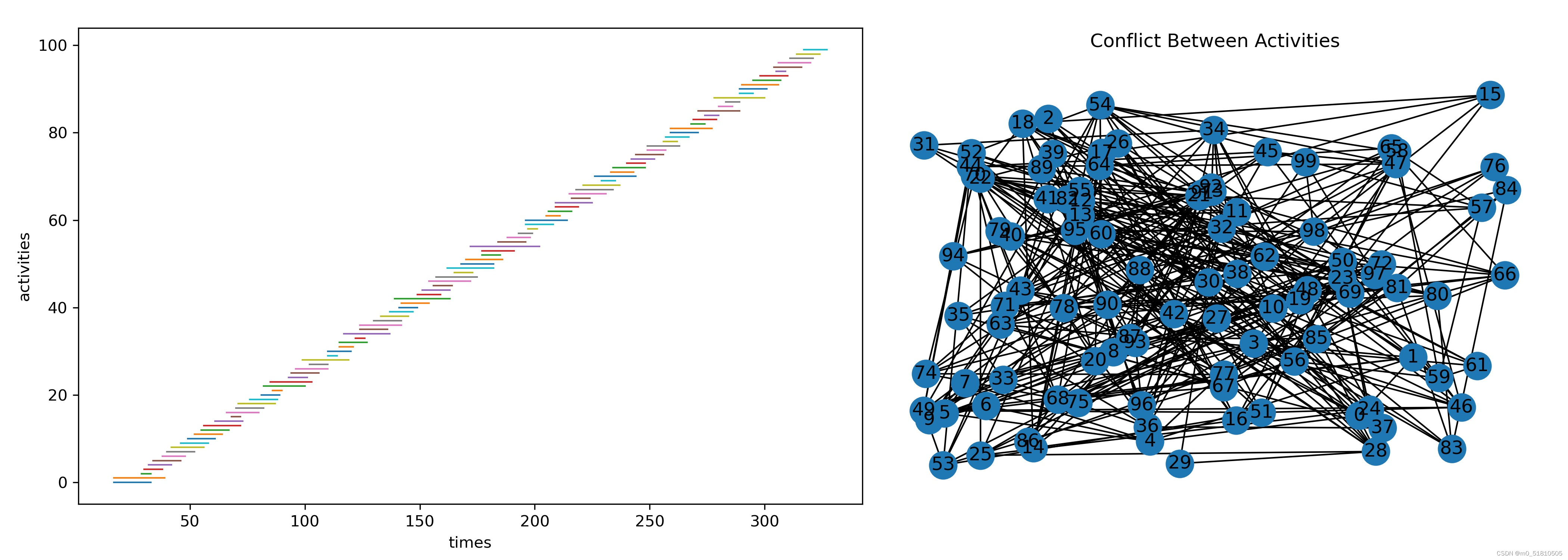
生成的冲突图有100个节点，325条边，平均度为6.5。把这个图用同样的方法送进GNN求解器中，结果如下：

Epoch: 9000, Loss: 0.05441362038254738
Stopping early on epoch 9673 (patience: 100)
GNN training (n=100) took 40.492
GNN final continuous loss: 0.03501168638467789
GNN best continuous loss: 0.0
Calculating violations...
Independence number found by GNN is 0.0 with 0 violations
Took 40.51s, model training took 40.492s
Running built-in MIS solver (n=100).
Calculating violations...
Independence number found by nx solver is 25 with 0 violations.
MIS solver took 0.0s

GNN求解器又寄了，还是一个最大独立集都没有找出来，而networkx求解器找到了25个。然而官方示例100个节点的随机图是能够跑出来的，怎么回事呢。

最后我发现：这个GNN求解器求解最大独立集的图，节点平均度不能太大。

猜测这可能和GNN网络的规模有关系，示例求解器的GNN深度只有2层，理论上只能捕获二跳邻接节点内的信息（在论文插图中也显示了这一点），这可能使得它难以处理平均度太大的图。因为平均度大的图，最大独立集节点可能过于稀疏，需要更深的GNN才能捕获更远的邻接信息。

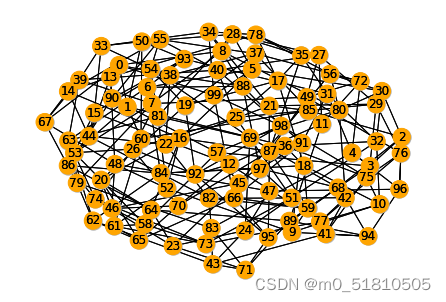
我修改了一下示例源码随机图的参数，尝试生成了一些平均度比较大的图。在最原始的100个节点随机图下，把平均度参数d从3改为5，其他不变，GNN求解器就已经一个最大独立集也找不出了，而networkx求解器能够找到31个，GNN求解器输出图如下：

然后回到论文的实验中，我们看到它的实验结果是这样的：

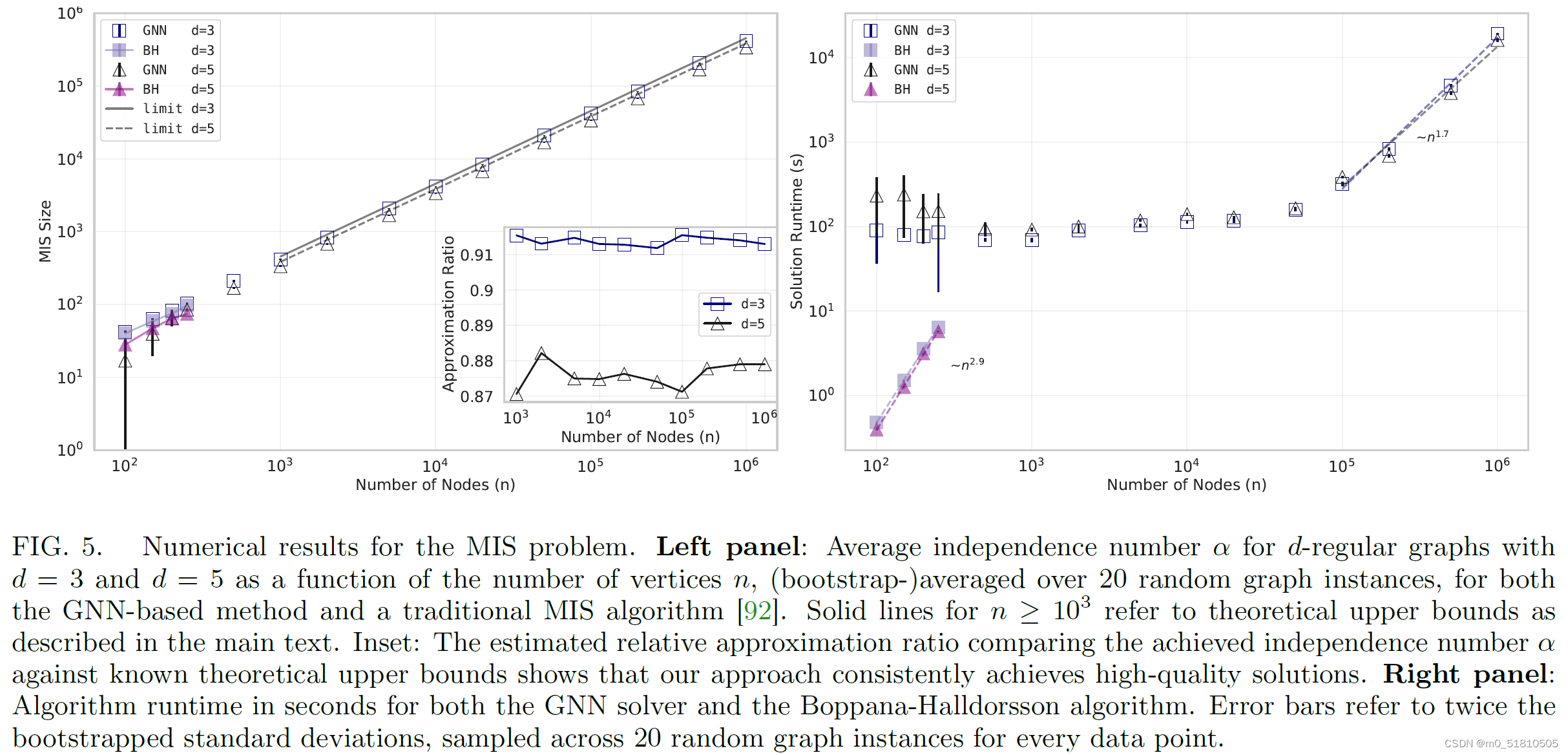
这个GNN求解器做的实验，只有d=3和d=5两种节点平均度，然而我的区间调度问题，节点度有6.5，这对于GNN求解器来说似乎太大了。

但是似乎随着求解规模的增加，节点度平均度可以适当的提高一些。同样在示例源码的情况下，只把节点数n改为800，把随机生成图的平均度d改为6，GNN求解器就能够找到一组节点数为241的最大独立集，然而networkx求解器只找到214个：

Epoch: 18000, Loss: -240.93582153320312
Stopping early on epoch 18999 (patience: 100)
GNN training (n=800) took 82.14
GNN final continuous loss: -240.9747314453125
GNN best continuous loss: -240.9747314453125
Calculating violations...
Independence number found by GNN is 241 with 0 violations
Took 82.262s, model training took 82.142s
Running built-in MIS solver (n=800).
Calculating violations...
Independence number found by nx solver is 214 with 0 violations.
MIS solver took 0.007s

需要注意的是，图的规模很大时（如1000节点），nx.draw()方法无法短时间内将图画出，导致程序阻塞无法运行。求解很大的图时需要将./gnn_example.ipynb中所有相关的绘图语句注释掉，以免拖累速度。

我尝试了10000个节点，d=8的随机图，GNN求解用时3分钟，得到2512个节点的最大独立集，networkx求解的最大独立集节点数是2398。我的设备上求解规模的极限是50000个节点，d=10的随机图，规模再大爆12g显存了。该图求解时cuda占用100%，GNN求解用时36分钟，得到10882个节点的最大独立集（有两个点不符合约束），networkx求解的最大独立集节点数是10604，用时18s。

那么事情就变得简单了。对于我们的区间调度问题，只要减少任务之间的冲突数量，也就是减少边数，就可以减少节点度了。通过改变泊松分布的均值，我生成了一个冲突规模更小的区间调度问题：

np.random.seed(9527)
aclist = np.arange(100)
bias = np.random.poisson(lam=2.2,size=[100,1])+1
activities = 3*np.arange(100).reshape(-1,1)+np.column_stack((-1*bias,bias))+25
# 查看图的基本属性，如下：
# mis(maximal_independent_set) nodes:[86, 73, 41, 96, 92, 58, 7, 45, 19, 34, 80, 3, 30, 11, 13, 50, 53, 26, 69, 57, 16, 0, 65, 9, 77, 38, 83, 22, 90, 72, 75, 5, 55, 47, 61, 28]
# num of coflicts(edges):153
# average degree:3.06

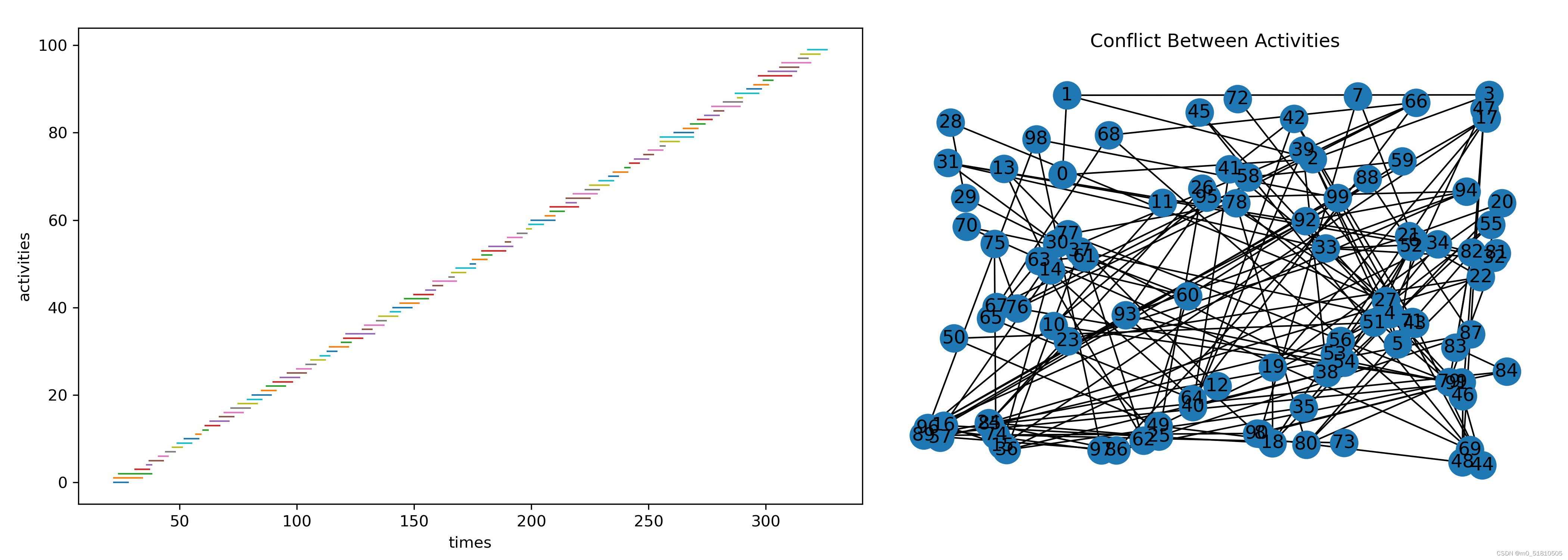
这一次，冲突图的平均节点度只有3.06了，把这个图用GNN求解器求解，结果如下：

nx_graph = nx.read_gpickle('./interval graph/PoissonIntervalGraph100.gpickle')

Epoch: 26000, Loss: -38.95990753173828
Stopping early on epoch 26889 (patience: 100)
GNN training (n=100) took 117.285
GNN final continuous loss: -38.977638244628906
GNN best continuous loss: -38.977638244628906
Calculating violations...
Independence number found by GNN is 39 with 0 violations
Took 117.301s, model training took 117.287s
Running built-in MIS solver (n=100).
Calculating violations...
Independence number found by nx solver is 35 with 0 violations.
MIS solver took 0.0s

求解这个区间调度问题对应冲突图的最大独立集，GNN求解器找到了39个节点的最大独立集，而networkx只找到了35个。GNN求解器所找到的这些独立节点，就是所对应的区间调度问题，所能完成的最多任务。

这样看来，这个GNN求解器还是可以解决一定的现实问题的，特别当这些问题的求解规模比较大时更好。而问题规模较小的时候，其表达为图上的问题时，节点平均度不能太高。总的来说，这个求解器还是有一定的应用价值的。

4 部分代码

画区间调度图与最大独立集.py

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

aclist = np.arange(9)
activities = np.array([[1,3], [0,5], [10,13], [1,6], [4,9], [8,12], [10,11], [2,7], [8,12]])
times = np.array([0,2,4,6,7,8,12,14,14.5,16,20,22,25,30])

fig=plt.figure(figsize=(10,3.5)) #初始化画布
ax1=fig.add_axes([0.08,0.13,0.63,0.79]) #ax的位置，[左，下，宽，高]
ax2=fig.add_axes([0.71,0.13,0.28,0.79])

# 画网格
ax1.plot(np.array([[-0.5]*9, [30.5]*9]), np.row_stack((aclist, aclist)), linewidth=0.5, c='gray')
ax1.plot(np.row_stack((times, times)), np.array([[-0.5]*14, [8.5]*14]), linewidth=0.5, c='gray')

# 画任务
for i in range(aclist.shape[0]):
    if i in [0,4,6]: ax1.plot(times[activities[i]], np.repeat(aclist[i], 2), linewidth=3, c='tab:orange', 
                              label='Do (MIS nodes)' if i==4 else None)
    else: ax1.plot(times[activities[i]], np.repeat(aclist[i], 2), linewidth=3, c='tab:blue',
                    label='Not do' if i==1 else None)

# for i in range(aclist.shape[0]):
#     if i in [0,4,6]: ax1.plot(times[activities[i]], np.repeat(aclist[i], 2), linewidth=3, c='black',
#                               label='Activity duration interval' if i==4 else None)
#     else: ax1.plot(times[activities[i]], np.repeat(aclist[i], 2), linewidth=3, c='black')

# 改tick
ax1.set_xlabel('times')
ax1.set_xticks(ticks=[i for i in times if i!=14.5])
ax1.set_yticks(ticks=aclist)
ax1.set_yticklabels(labels=[f'activity{j}' for j in aclist])
ax1.set_title('Interval Graph (Do as many activities as possible, with one thread)')
# ax1.set_title('Interval Graph')
ax1.legend(loc='lower right')

# ax2
def collision(act12):
    # collision if max(act1.start, act2.start)<min(act1.end, act2.end)
    return True if act12.max(axis=0)[0]<act12.min(axis=0)[1] else False

# 遍历检测冲突，有冲突则构建一条边
edgelist=[]
for i in range(aclist.shape[0]):
    for j in range(i+1,aclist.shape[0]):
        if collision(activities[[i,j]]):
            edgelist.append((aclist[i], aclist[j]))

G = nx.Graph()
G.add_nodes_from(aclist)
G.add_edges_from(edgelist)

# https://networkx.org/documentation/latest/auto_examples/drawing/plot_degree.html#sphx-glr-auto-examples-drawing-plot-degree-py
pos = nx.spring_layout(G, seed=6689)
color_map = ['tab:orange' if node in [0,4,6] else 'tab:blue' for node in G.nodes]
# color_map = ['tab:blue' for node in G.nodes]
nx.draw(G, pos, with_labels=True, node_color=color_map, ax=ax2)
ax2.set_title('Maximal Independent Set')
# ax2.set_title('Conflict Between Activities')
ax2.set_axis_off()

# plt.savefig('interval graph with MIS.jpg', dpi=300)
# plt.savefig('interval graph with MIS black.jpg', dpi=300)

用泊松分布生成间隔调度任务.py

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from networkx.algorithms.mis import maximal_independent_set as mis

np.random.seed(9527)
aclist = np.arange(100)
bias = np.random.poisson(lam=2.2,size=[100,1])+1
activities = 3*np.arange(100).reshape(-1,1)+np.column_stack((-1*bias,bias))+25
# np.random.shuffle(activities)

def collision(act12):
    # collision if max(act1.start, act2.start)<min(act1.end, act2.end)
    return True if act12.max(axis=0)[0]<act12.min(axis=0)[1] else False

# 遍历检测冲突，有冲突则构建一条边
edgelist=[]
for i in range(100):
    for j in range(i+1,100):
        if collision(activities[[i,j]]):
            edgelist.append((i,j))

# G = nx.Graph()
G = nx.OrderedGraph()
G.add_nodes_from(aclist)
G.add_edges_from(edgelist)
nx.write_gpickle(G,'PoissonIntervalGraph100.gpickle')

print(f'mis(maximal_independent_set) nodes:{mis(G)}')
print(f'num of coflicts(edges):{len(G.edges)}')
print(f'average degree:{np.array(G.degree).mean(axis=0)[1]}')

# 画图
fig=plt.figure(figsize=(14,5))
ax1=fig.add_axes([0.05,0.1,0.5,0.85]) #[左，下，宽，高]
ax2=fig.add_axes([0.55,0.1,0.45,0.8])

for i in range(100):
    ax1.plot(activities[i],[i,i], linewidth=1)
ax1.set_xlabel('times')
ax1.set_ylabel('activities')

nx.draw(G, pos=nx.random_layout(G), with_labels=True, ax=ax2)
ax2.set_title('Conflict Between Activities')

# plt.savefig('poisson interval graph with 100 nodes.jpg', dpi=300)

若有不对之处，希望各位大佬指正
完结撒花~