循环神经网络理论

引用翻译：《动手学深度学习》

一、递归神经网络

在n-gram模型中，单词wt在位置t的条件概率只取决于之前的n-1个单词。如果我们想检查比t-(n-1)更早的词对wt可能产生的影响，我们需要增加n。然而，模型参数的数量也会随之呈指数级增加，因为我们需要为一个词汇表V存储|V|n个数字。因此，与其建立p(wt|wt-1;. . ;wt-n+1)模型，不如使用潜变量模型，其中我们有

𝑝(𝑥𝑡|𝑥𝑡-1,…𝑥1)≈𝑝(𝑥𝑡|𝑥𝑡-1,?𝑡) 。

对于一个足够强大的函数ht来说，这并不是一个近似值。毕竟，ht可以简单地存储它到目前为止观察到的所有数据。让我们来看看为什么建立这样的模型比简单的自回归模型要棘手一些，其中

?𝑡=𝑓(𝑥𝑡-1, ?𝑡-1)。

作为热身，我们将回顾后者的离散输出和n=2的情况，即一阶马尔可夫模型。为了进一步简化事情，我们在设计RNN时使用单层。稍后我们将看到如何有效地增加跨项的表达能力。

二、没有隐藏状态的递归网络

让我们看一下具有单一隐藏层的多层感知器。给出一个小型批次的实例X Rn * d，样本大小为n，输入为d（特征或特征向量尺寸）。让隐藏层的激活函数为j。因此，隐藏层的输出HRn * h被计算为

$\mathbf{H} = \phi(\mathbf{X} \mathbf{W}_{xh} + \mathbf{b}_h).$

这里，我们有权重参数Wxh ~ Rd * h，偏置参数bh ~ R1 * h，以及隐藏单元的数量h，用于隐藏层。回顾一下，bh只是一个向量–它的值是使用广播机制复制的，以匹配矩阵-矩阵乘积的值。

还要注意，隐藏状态和隐藏层指的是两个非常不同的概念。正如所解释的那样，隐藏层是在从输入到输出的路径上被隐藏起来的层。严格来说，隐藏状态是对我们在某一步骤所做的任何事情的输入。相反，它们只能通过查看以前迭代的数据来计算。在这个意义上，它们与统计学中的潜变量模型有很多共同之处，比如聚类或主题模型，其中聚类ID会影响输出，但不能直接观察到。

隐藏变量H被用作输出层的输入。对于分类的目的，例如预测下一个字符，输出维度q可能与分类问题中的类别数量相匹配。最后，输出层是由

$\mathbf{O} = \mathbf{H} \mathbf{W}_{hq} + \mathbf{b}_q.$

这里，O ~ R^{n * q}是输出变量，W_hq ~ R^{h * q}是权重参数，b_q ~ R^{1 * q}是输出层的偏置参数。如果是分类问题，我们可以用softmax(O)来计算输出类别的概率分布。我们可以随机挑选(wt;wt-1)对，通过autograd和随机梯度下降估计我们网络的参数W和b。

三、具有隐藏状态的递归网络

当我们有隐藏状态时，事情就完全不同了。让我们更详细地看一下这个结构。假设X_t ~ R^{n * d}是小批量输入，H_t ~ R^{n * h}是序列中时间步骤t的隐藏变量。与多层感知器不同，这里我们保存了前一个时间步骤的隐藏变量Ht-1，并引入一个新的权重参数W_hh ~ R^{h * h}，以描述如何在当前时间步骤中使用前一个时间步骤的隐藏变量。具体来说，当前时间步骤的隐藏变量的计算是由当前时间步骤的输入与前一时间步骤的隐藏变量共同决定的。

$\mathbf{H}t = \phi(\mathbf{X}t \mathbf{W}{xh} + \mathbf{H}{t-1} \mathbf{W}_{hh} + \mathbf{b}_h).$

与多层感知器相比，我们在这里多加了一个H_t-1W_hh。从相邻时间步骤的隐藏变量Ht和Ht-1之间的关系来看，我们知道这些变量捕捉并保留了序列的历史信息，直到当前时间步骤，就像神经网络当前时间步骤的状态或记忆。因此，这样的隐藏变量也被称为隐藏状态。由于隐藏状态在当前时间步骤中使用了前一个时间步骤的相同定义，所以上述方程的计算是递归的，因此被称为递归神经网络（RNN）。

有许多不同的RNN构建方法。具有由上述方程定义的隐藏状态的RNN是非常常见的。对于时间步骤t，输出层的输出与多层感知器中的计算类似。

$\mathbf{O}_t = \mathbf{H}t \mathbf{W}{hq} + \mathbf{b}_q$

RNN的参数包括隐藏层的权重W_xh ~ R^{d * h}; W_hh ~ R^{h * h}，偏置b_h ~ R^{1 * h}，以及输出层的权重W_hq ~ R^{h * q}，偏置b_q ~ R^{1 * q}。值得一提的是，RNN总是使用这些模型参数，即使是不同的时间步骤。因此，RNN模型参数的数量不会随着时间步数的增加而增长。

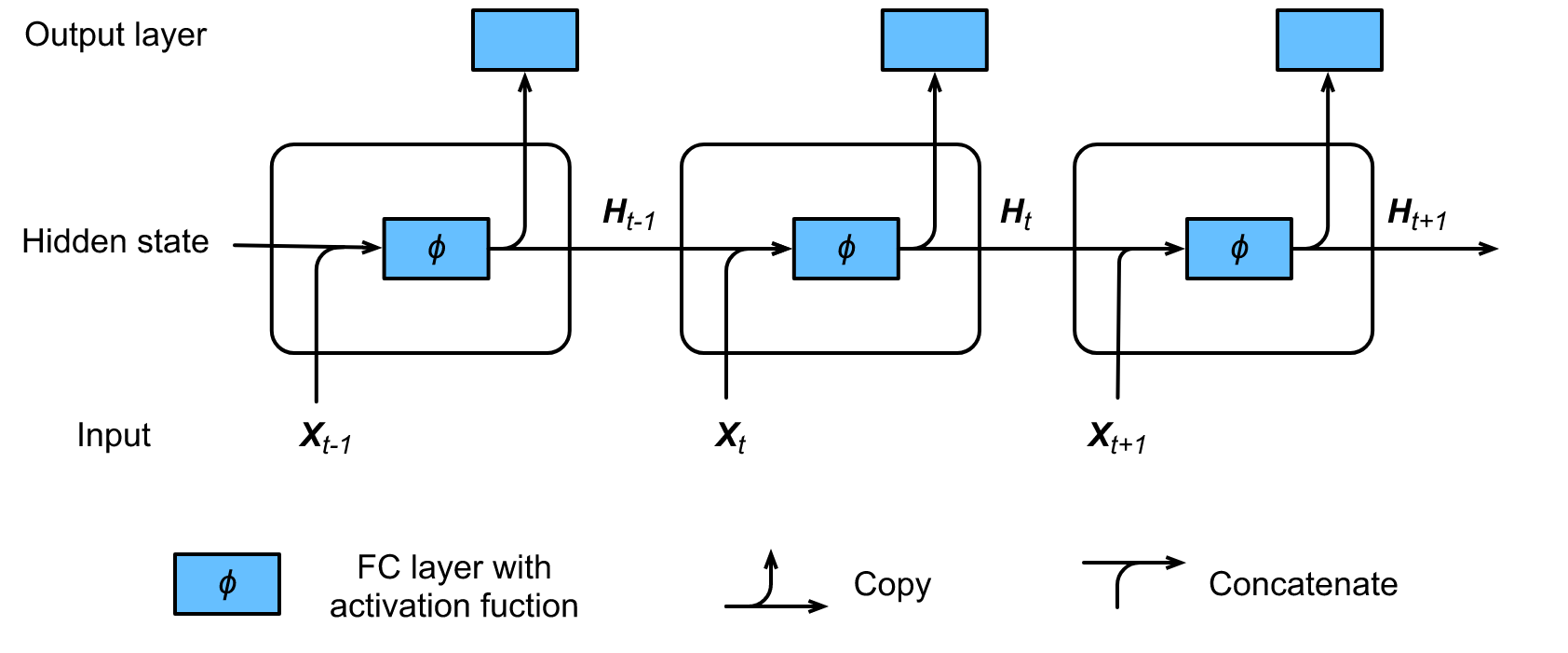
下图显示了一个RNN在三个相邻时间步长的计算逻辑。在时间步数t中，隐藏状态的计算可以被看作是将输入Xt与前一个时间步数的隐藏状态Ht-1串联后，带有激活函数j的全连接层的一个入口。全连接层的输出是当前时间步骤的隐藏状态Ht。其模型参数是Wxh和Whh的串联，偏置为bh。当前时间步骤t的隐藏状态Ht将参与计算下一个时间步骤t+1的隐藏状态Ht+1，其结果将成为当前时间步骤的全连接输出层的输入。
在这里插入图片描述

如前所述，隐藏状态下的计算使用H_t = X_tW_xh + H_t-1W_hh 来生成在维度上与Ht-1相匹配的对象。此外，我们使用Ht来生成输出O_t = H_tW_hq.。

import torch
import torch.nn as nn

X=torch.randn(3,1)
H=torch.randn(3,2)

W_xh=torch.randn(1,2)
W_hh=torch.randn(2,2)
W_hq=torch.randn(2,3)

def net(X, H):
    H = (torch.mm(X, W_xh) + torch.mm(H, W_hh))
    O = (torch.mm(H, W_hq))
    return H, O

上面定义的递归网络将观察结果X和隐藏状态H作为参数，并使用它们来更新隐藏状态并发出输出O。

由于这个链条可能会持续很长的时间，用Backprop训练模型是不可能的（至少没有一些近似值）。

毕竟，这导致了一个非常长的依赖链，要准确解决这个问题是很困难的：书籍通常有超过100,000个字符，假设后来的文本不加区分地依赖所有发生的情况，

例如，在过去的10,000个字符，是不合理的。像BPTT和长短时记忆这样的截断方法对于以更有原则的方式解决这个问题很有用。现在，让我们看看状态更新是如何工作的。

(H, O) = net(X,H)

print(H)
print(O)

tensor([[-0.1791, -1.1110],
        [ 1.8311, -4.8133],
        [ 0.1405,  2.0094]])
tensor([[ 1.4982, -0.4124,  0.5771],
        [ 2.0720, -1.2001,  2.6391],
        [-2.3988,  0.7046, -1.0535]])

四、语言模型的步骤

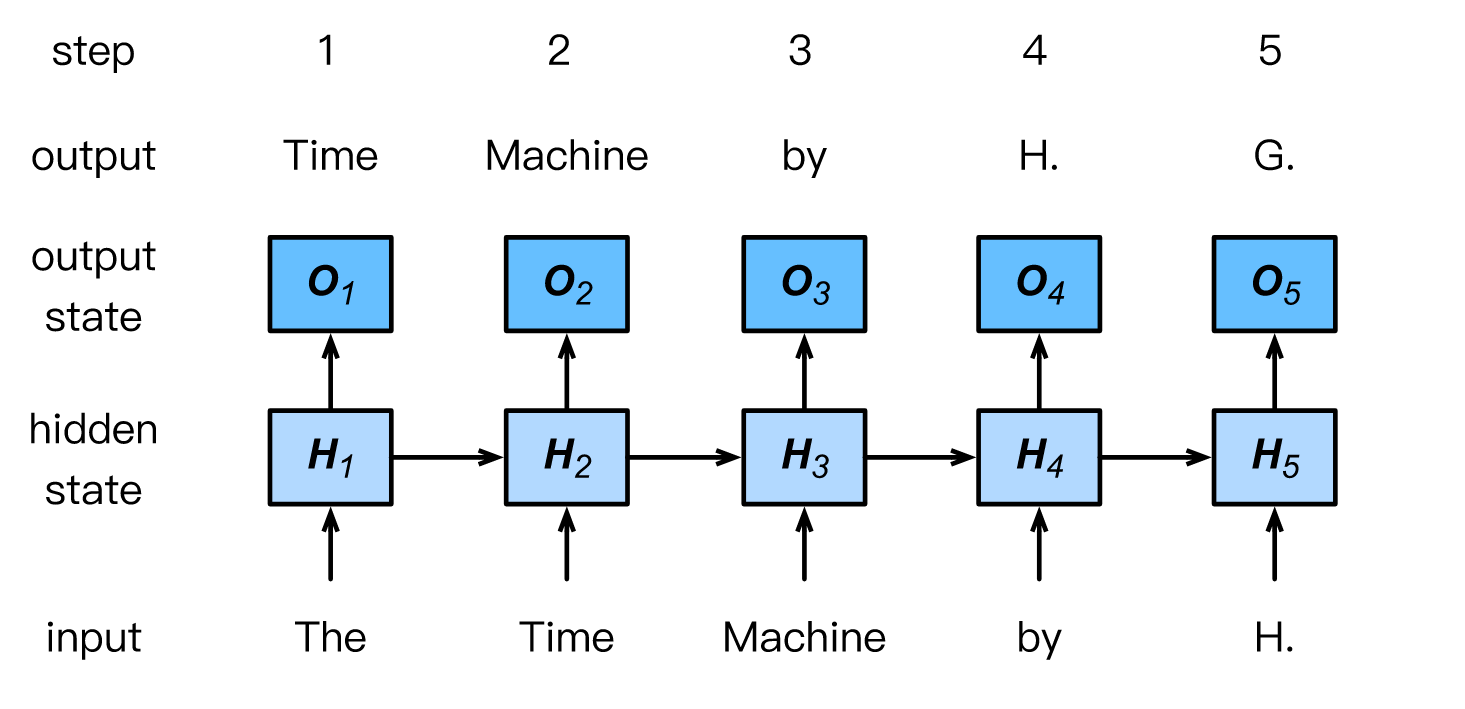
在本节的最后，我们将说明RNN如何用于建立语言模型。为了简单起见，我们使用单词而不是字符，因为前者更容易理解。让小批量例子的数量为1，文本的序列是我们数据集的开始，即 “h.g.wellls的时间机器”。下图说明了如何根据现在和以前的字符来估计下一个字符。在训练过程中，我们对每个时间步长的输出层的输出进行softmax运算，然后使用交叉熵损失函数来计算结果和标签之间的误差。由于隐藏层中隐藏状态的循环计算，时间步骤3 O3的输出是由文本序列 “the”, “time”, "machine "决定。由于训练数据中序列的下一个词是 “by”，时间步骤3的损失将取决于基于序列 “the”、“time”、"machine "和这个时间步骤的标签 "by "产生的下一个词的概率分布。

在这里插入图片描述